Sets
Class-9-Mathematics-1-Chapter-1-Maharashtra Board
Solutions- Practice Set and Problem Sets
Practice set 1.1
(1) Write the following sets in roster form.
(i) Set of even numbers
- A = {2, 4, 6, 8, 10, ...}
(ii) Set of even prime numbers from 1 to 50
- P = {2}
(iii) Set of negative integers
- I = { …., -4, -3, -2, -1}
(iv) Seven basic sounds of a sargam (sur)
- M = {sa, re, ga, ma, pa dha, ni}
(2) Write the following symbolic statements in words.
(i) 4/3 ∈ Q
- 4/3 is an element of the set Q.
(ii) −2 ∉ N
- −2 is not an element of the set N.
(iii) P = {p| p is an odd number}
- Set P is a set of all p’s such that p is an odd number.
(3) Write any two sets by listing method and by rule method.
(i) Listing method :
A = {Hindi, English, Mathematics, Science, History, Geography, Political Science}
Rule method :
A = {x | x is a subjects of class 10}
(ii) Listing method : B ={ — 4, -3, -2, — 1, 0, 1, 2, 3}.
Rule method : B = {x ∈ I, — 5 < x < 4}.
(4) Write the following sets using listing method.
(i) All months in the indian solar year.
- A = { Chaitra, Vaishakha, Jyestha, Aashadha, Shravana, Bhadrapada, Ashwina, Kartika, Margashirsha, Pausha, Magha, Falguna}
(ii) Letters in the word ‘COMPLEMENT’.
- W = {C, O, M, P, L, E, N, T}
(iii) Set of human sensory organs.
- O = {Nose, Ears, Eyes, Tongue, Skin}
(iv) Set of prime numbers from 1 to 20.
- P = {2, 3, 5, 7, 11, 13, 17, l9}
(v) Names of continents of the world.
- C = {Asia, Africa, North America, South America, Antarctica, Europe, Australia}
(5) Write the following sets using rule method.
(i) A = { 1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
- A= {x | x = n2, n ∈ N, n ≤ 10}
(ii) B = { 6, 12, 18, 24, 30, 36, 42, 48}
- B = {x | x= 6n, n ∈ N, n< 9}
(iii) C = {S, M, I, L, E}
- C = { y | y is a letter in the word ‘MISSILE’}
(iv) D = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
- D = {z | z is a day of the week}
(v) X = {a, e, t}
- X = {y |y is a letter in the word ‘eat’ or ‘tea’.}
Practice set 1.2
(1) Decide which of the following are equal sets and which are not ? Justify your answer.
A = { x | 3x − 1 = 2}
B = { x | x is a natural number but x is neither prime nor composite}
C = {x | x ∈ N, x < 2}
(i) A = {x | 3x − 1 = 2}
3x − 1=2 ∴ 3x = 2 + 1 ∴ 3x = 3
∴ x = 1 …..(1)
(ii) B = {x | x is a natural number but x is neither prime nor composite}
1 is the only natural number which is neither prime nor composite.
∴ x = 1 ….(2)
(iii) C = {x | x ∈ N, x < 2}
1 is the only natural number less than 2.
∴ x =1. ……(3)
From (1), (2) and (3), the sets A, B and C are equal sets, because they contain the same element, namely 1.
(2) Decide whether set A and B are equal sets. Give reason for your answer.
(i) A = Even prime numbers (ii) B = {x | 7x − 1 = 13}
(i) A = {2}, because 2 is the only even prime number. …..(1)
(ii) B = {x|7x − 1 = 13}. 7x − 1 = 13
7x = 13 + 1 ∴ 7x = 14
∴ x = 2. ……(2)
From (1) and (2), the sets A and B arc equal sets because they contain the same element, namely 2.
(3) Which of the following are empty sets ? why ?
(i) A = { a | a is a natural number smaller than zero.}
(ii) B = {x | x2 = 0}
(iii) C = { x | 5 x − 2 = 0, x ∈ N}
(i) There is no natural number smaller than zero
∴ A ={ }. i.e. set A is an empty set.
(ii) X2 = 0. x = 0. Set B has an element 0.
∴ set B is not an empty set.
(iii) 5x – 2 = 0. ∴ .5x = 2. ∴ .x =
x ∈ N given. But is not a natural number.
∴ set C is an empty set.
(4) Write with reasons, which of the following sets are finite or infinite.
(i) A = { x | x < 10, x is a natural number}
- A= {1, 2, ..., 8, 9}. setA is a finite set.
(ii) B = {y | y < -1, y is an integer}
- B={..., -4, —'3, —2}. setB is an infinite set.
(iii) C = Set of students of class 9 from your school.
- C = {The number of students in a class is countable}. set C is a finite set.
(iv) Set of people from your village.
- The number of people in a village is countable. this set is a finite set.
(v) Set of apparatus in laboratory
- The set of apparatus in a laboratory is not large. this set is a finite set.
(vi) Set of whole numbers
- The set of whole numbers is an infinite set, because the counting do not terminate at any stage.
(vii) Set of rational number
- There are infinite rational numbers. ∴ this set is an infinite set.
(Finite Sets : (i), (iii), (iv), (v), Infinite Sets : (ii), (vi), (vii))
Practice set 1.3
(1) If A = {a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = {a, e} then which of the following statements are true and which are false ?
(i) C ⊆ B (ii) A ⊆ D (iii) D ⊆ B (iv) D ⊆ A (v) B ⊆ A (vi) C ⊆ A
(i) False : Element b of set C is not in set B.
(ii) False : All the elements of set A are not in set D.
(iii) False : Element a of set D is not in set B.
(iv) True : Elements a and e both of set D are also in set A.
(v) False : Element f of set B is not in set A.
(vi) True : Elements b and d both of set C are in set A.
(2) Take the set of natural numbers from 1 to 20 as universal set and show set X and Y using Venn diagram.
(i) X = { x | x ∈ N, and 7 < x < 15}
(ii) Y = { y | y ∈ N, y is prime number from 1 to 20}
(i) U = {1, 2, 3,….., 18, 19, 20} X = {8, 9, 10, 11, 12, 13, 14}
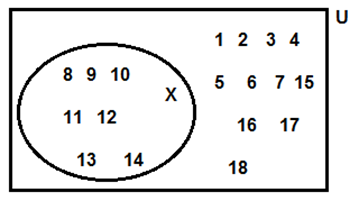
(ii) U = {1, 2, 3,….., 18, 19, 20} Y = {2, 3, 5, 7, 11, 13, 17, 19}
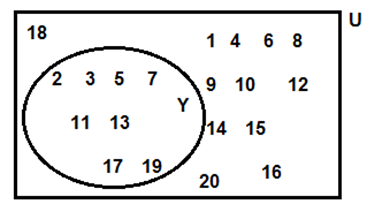
(3) U = {1, 2, 3, 7, 8, 9, 10, 11, 12} P = {1, 3, 7, 10} then
(i) show the sets U, P and P’ by Venn diagram.
(ii) Verify (P’)’ = P
(i) U = {l, 2, 3, 7, 8, 9, 10, 11 }
P = {1, 3, 7, 10}
∴ P’ = {2, 8, 9, 11, 12}

(ii) U = {1, 2, 3, 7, 8, 9, 10, 11, 12}
P’= {2, 8, 9, 11, 12}
∴ (P’)’= U ∩ P’ = {1, 3, 7, 10} ……(1)
P = {l, 3, 7, 10} ……..(Given) (2)
From (1) and (2), (P’)’ = P.
(4) A = {1, 3, 2, 7} then write any three subsets of A.
The subsets of set A are as follows : (OEQ)
Φ , {1}, {3}, {3, 2}, {1, 2, 7}, { 1, 3, 2, 7}.
[Note : Student can write any three subsets from above. ]
(5) (i) Write the subset relation between the sets.
- P is the set of all residents in Pune.
- M is the set of all residents in Madhya Pradesh.
- I is the set of all residents in Indore.
- B is the set of all residents in India.
- H is the set of all residents in Maharashtra.
(ii) Which set can be the universal set for above sets ?
(i) All the residents of Pune are also the residents of Maharashtra. ∴ P ⊆ H.
All the residents of Pune are also the residents of India. ∴ P ⊆ B.
All the residents of Indore are also the residents of Madhya Pradesh. ∴ I ⊆ M.
All the residents of Indore are also the residents of India. ∴ I ⊆ B.
All the residents of Madhya Pradesh are also the residents of India. ∴ M ⊆ B.
All the residents of Maharashtra are also the residents of India. ∴ H ⊆ B.
(ii) From above, all the sets are the subsets of B.
∴ B, the set of all residents of India, can be chosen as the universal set.
(6*) Which set of numbers could be the universal set for the sets given below?
(i) A = set of multiples of 5, B = set of multiples of 7. C = set of multiples of 12
(ii) P = set of integers which are multiples of 4. T = set of all even square numbers.
N = {1, 2, 3, ...}; W = {0, 1, 2, 3, ...}; I = {..., -3, -2, -1, 0, 1, 2, 3, ...}.
(i) A= {5, 10, 15, ...}; B = {7, 14, 21, ...}; C = {12, 24, 36, ...}
Sets A, B and C are the subsets of N, W as well as I.
Any of the sets N, W or I can be taken as an universal set, for the sets A, B and C.
(ii) P = {4, 8, 12, ....}
T = {22, 42, 62, ...}
Any of the sets N, W or I can be taken as an universal set for the sets P and T.
(7) Let all the students of a class is an Universal set. Let set A be the students who secure 50% or more marks in Maths. Then write the complement of set A.
A’ = {The set of students, who secured less than 50% marks in Maths.}
Practice set 1.4
(1) If n (A) = 15, n (A ∪ B ) = 29, n (A ∩ B) = 7 then n (B) = ?
n(A ∪ B) = n(A) + n(B)—n(A ∩ B) ...(Rule)
∴ 29 = 15 + n(B)—7 ….. (Substituting the given values)
∴ n(B) = 29—15 + 7 ∴ n(B) = 2l
Answer is : n(B) = 21.
(2) In a hostel there are 125 students, out of which 80 drink tea, 60 drink coffee and 20 drink tea and coffee both. Find the number of students who do not drink tea or coffee.
Let U be the universal set of all the students in the hostel.
Let T be the set of students drinking tea and C be the set of students drinking coffee.
Then from the given information, n(U) = 125
n(T) = 80, n(C) = 60 and n(T ∩ C) = 20.
Now, n(T ∪ C) = n(T) + n(C) — n(T ∩ C) …..(Rule)
n(T ∪ C) = 80 + 60 — 20 = 120 ….. (Substituting the given values)
i.e. 120 students out of 125 drink tea or coffee or both.
The number of students who do not drink tea or coffee
= n(U) — n(T ∪ C) = 125 — 120 = 5.
Answer is : The number of students who do not drink tea or coffee is 5.
Alternative Method :
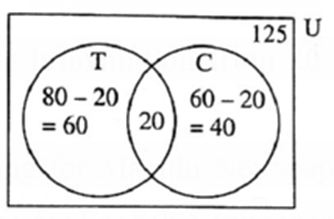
n(T ∪ C) = 60 + 20 + 40 = 120
n(U)—n(T ∪ C)= 125 -120 = 5
Answer is : The number of students who do not drink tea or coffee is 5.
(3) In a competitive exam 50 students passed in English. 60 students passed in Mathematics. 40 students passed in both the subjects. None of them fail in both the subjects. Find the number of students who passed at least in one of the subjects ?
Let set E = the number of students who passed in English.
set M = the number of students who passed in Mathematics.
Then n(E) = 50, n(M) = 60 and n (E ∩ M) = 40.
Now, n(E ∪ M) = n(E) + n(M) — n(E ∩ M) …...(Rule)
= 50 + 60 — 40 = 70 …. (Substituting the given values)
Answer is : 70 students passed either in English or in Mathematics. i.e. the total number of students is 70.
Alternative Method :
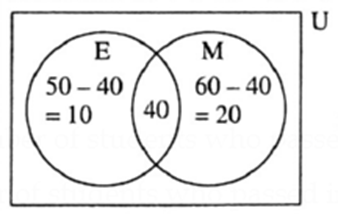
n(E ∪ M) = 10 + 40 + 20 = 70
Answer is : The total number of students is 70 = n(E ∪ M)
(4*) A survey was conducted to know the hobby of 220 students of class IX. Out of which 130 students informed about their hobby as rock climbing and 180 students informed about their hobby as sky watching. There are 110 students who follow both the hobbies.
Then how many students do not have any of the two hobbies ? How many of them follow the hobby of rock climbing only ? How many students follow the hobby of sky watching only ?
Let R be the set of students having rock climbing hobby. Then n (R) = 130.
S be the set of students having sky watch hobby. Then n(S) = 180.
Total number of students : n (U) = 220
The number of students having any of the two hobbies = n(R ∩ S) = l10
n(R ∪ S)= n(R) + n(S)—n(R ∩ S) …..(Rule)
= 130 + 180 – 110 …….(Substituting the given values)
= 310 — 110 = 200.
The number of students not having both the hobbies.
= n(U) —n(R ∪ S)
= 220 — 200 = 20
The number of students having only rock climbing hobby, _
= n(R) — n(R ∩ S)
= 130 — 110 = 20
The number of students having only sky watch hobby
= n(S) — n(R ∩ S)
= 180 — 110 = 70
Answer is . 20 students do not have any hobby.
20 students follow only rock climbing hobby.
70 students follow only sky watch hobby.
Alternative Method :
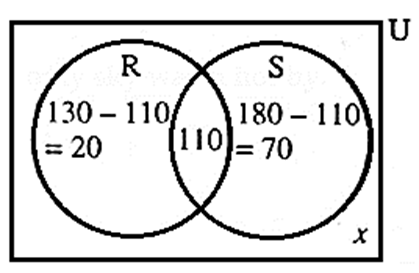
Let x be the number of students not having both the hobbies.
x = n(U) — n(R ∪ S) = 220 — (20 + 110 + 70) = 220 — 200 = 20
The number of students having only rock climbing hobby
= n(R) —n(R ∩ S) = 130 - 110 = 20.
The number of students having only skywatch hobby
= n(S) — n(R ∩ S) = 180 - 110 = 70.
Answer is . 20 students do not have any hobby.
20 students follow only rock climbing hobby.
70 students follow only sky watch hobby.
(5) Observe the given Venn diagram and write the following sets.
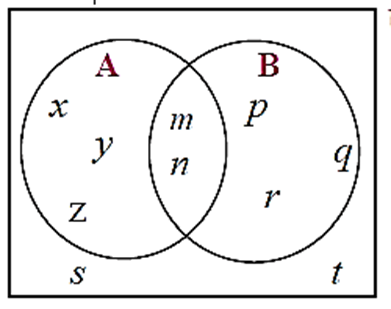
(i) A (ii) B (iii) A ∪ B (iv) U (v) A’ (vi) B’ (vii) (A ∪ B)’
(i) A= {x, y, z, m, n}
(ii) B = {p, q, r, m, n}
(iii) A ∪ B = {x, y, z, p, q, r, m, n}
(iv) U = {x, y, z, m, n, p, q, r, s, t}
(V) A' = {p, q, r, s, t}
(Vi) B’ = {x, y, z, s, t}
(vii) (A ∪ B)’ = {s, t}
Problem set 1
(1) Choose the correct alternative answer for each of the following questions.
(i) If M = {1, 3, 5}, N = {2, 4, 6}, then M ∩ N = ?
(A) {1, 2, 3, 4, 5, 6}
(B) {1, 3, 5}
(C) Φ
(D) {2, 4, 6}
(C) Φ [There is no common element in the sets M and N.]
(ii) P = {x | x is an odd natural number, 1 < x ≤ 5} How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
(D) {3, 5} [As per the condition, 3 and 5 are the required numbers.]
(iii) P = {1, 2, ........., 10}, What type of set P is ?
(A) Null set
(B) Infinite set
(C) Finite set
(D) None of these
(C) Finite set [The number of elements are countable.]
(iv) M ∪ N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4} then which of the following represent set N ?
(A) {1, 2, 3}
(B) {3, 4, 5, 6}
(C) {2, 5, 6}
(D) {4, 5, 6}
(B) {3, 4, 5, 6} [along with 1, 2, 4 make M ∪ N.]
(v) If P ⊆ M, then Which of the following set represent P ∩ (P ∪ M) ?
(A) P
(B) M
(C) P ∪ M
(D) P’ ∩ M
(A) P [Refer to Note under the question.]
(vi) Which of the following sets are empty sets ?
(A) set of intersecting points of parallel lines
(B) set of even prime numbers.
(C) Month of an english calendar having less than 30 days.
(D) P = {x | x ∈ I, -1 < x < 1}
(A) set of intersecting points of parallel lines [Parallel lines do not intersect]
(2) Find the correct option for the given question.
(i) Which of the following collections is a set ?
(A) Colours of the rainbow
(B) Tall trees in the school campus.
(C) Rich people in the village
(D) Easy examples in the book
(A) Colours of the rainbow [The others are relative terms.]
(ii) Which of the following set represent N ∩ W?
(A) {1, 2, 3, .....}
(B) {0, 1, 2, 3, ....}
(C) {0}
(D) { }
(A) {1, 2, 3, .....}
(iii) P = {x | x is a letter of the word ' indian'} then which one of the following is set P in listing form ?
(A) {i, n, d}
(B) {i, n, d, a}
(C) {i, n, d, i, a}
(D) {n, d, a}
(B) {i, n, d, a} [This represents all the elements of the word ‘ indian’.]
(iv) If T = {1, 2, 3, 4, 5} and M = {3, 4, 7, 8} then T ∪ M = ?
(A) {1, 2, 3, 4, 5, 7}
(B) {1, 2, 3, 7, 8}
(C) {1, 2, 3, 4, 5, 7, 8}
(D) {3, 4}
(C) {1, 2, 3, 4, 5, 7, 8}
(3) Out of 100 persons in a group, 72 persons speak English and 43 persons speak French. Each one out of 100 persons speak at least one language. Then how many speak only English ? How many speak only French ? How many of them speak English and French both ?
Let E be the set of people speaking English and
F, the set of people speaking French.
Then n(E) = 72 and n(F) = 43.
All the 100 people speak one of the languages.
∴ n(E ∪ F) = 100
n(E ∪ F) = n(E) + n(F)—n(E ∩ F) ...(Rule)
100 = 72 + 43 — n(E ∩ F) ….. (Substituting the given values)
100 = 115 — n(E ∩ F)
∴ n(E ∩ F) = 115 — 100 ∴ n(E ∩ F) = l5
It means, 15 people speak both the languages.
The people who speak only English
= n(E) — n(E ∩ F) = 72 — 15 = 57
The people who speak only French
= n(F) — n(E ∩ F) = 43 — 15 = 28
Answer is : 57 people speak only English. 28 people speak only French. 15 people speak both the languages.
Alternative Method

Suppose x people speak both the languages.
n(E ∪ F) = 100 ……(Given)
72 —x + x + 43 —x = 100
115—x = 100 ∴ x = ll5 — l00 = 15
∴ 15 people speak both the languages.
People speaking only English = 72 — x = 72 — 15 = 57
People speaking only French = 43 — x = 43 — l5 = 28
Answer is : 57 people speak only English.
28 people speak only French.
15 people speak both the languages.
(4) 70 trees were planted by Parth and 90 trees were planted by Pradnya on the occasion of Tree Plantation Week. Out of these; 25 trees were planted by both of them together. How many trees were planted by Parth or Pradnya ?
Let P represent the number of trees planted by Parth.
n(P) = 70.
Let A represent the number of trees planted by Pradnya.
n(A) = 90.
25 trees were planted by both.
n(P ∩ A) = 25.
n(P ∪ A) = n(P) + n(A) — n(P ∩ A) …..(Rule)
= 70 + 90 — 25 ….. (Substituting the given values)
= 160 — 25 = 135
Answer is : The number of trees planted by Parth or Pradnya is 135.
(5) If n (A) = 20, n (B) = 28 and n(A ∪ B) = 36 then n(A ∩ B) = ?
n(A ∪ B) = n(A) + n(B)—n(A ∩ B) ….(Rule)
36 = 20 + 28 — n(A ∩ B) …… (Substituting the given values)
36 = 48 — n(A ∩ B)
n(A ∩ B) = 48 — 36 = 12
Answer is : n(A ∩ B) = 12.
(6) In a class, 8 students out of 28 have a dog as their pet animal at home, 6 students have a cat as their pet animal. 10 students have dog and cat both, then how many students do not have a dog or cat as their pet animal at home ?
Let D denote the number of student having dog as pet and C denote the number of student having cat as pet.
n(D) = The number of students having only dogs as pets + those having dogs and cats both as pets
n(D) = 8 + 10 = 18
Similarly, n(C) = 6 + 10 = 16
The number of students having both dogs and cats as pets = n(D ∩ C) = 10.
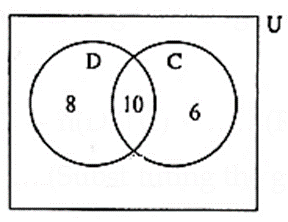
n(D ∪ C) = n(D) + n(C) — n(D ∩ C) ……(Rule)
= 18 + 16 — 10 …… (Substituting the given values)
= 34 — 10 = 24
The number of students who do not have a dog or a cat as pet = n(U) — n(D ∪ C)
= 28 — 24 = 4.
Answer is : 4 students do not have a dog or a cat as pet.
(7) Represent the union of two sets by Venn diagram for each of the following.
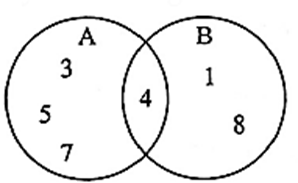
(i) A = {3, 4, 5, 7} B = {1, 4, 8}
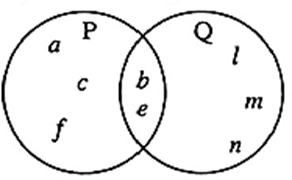
(ii) P = {a, b, c, e, f} Q = {l, m, n , e, b}
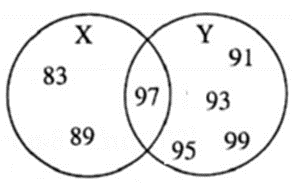
(iii) X = {x | x is a prime number between 80 and 100}
Y = {y | y is an odd number between 90 and 100 }
X= {83, 89, 97}
Y = {9l, 93, 95, 97, 99}
(8) Write the subset relations between the following sets..
X = set of all quadrilaterals. Y = set of all rhombuses.
S = set of all squares. T = set of all parallelograms.
V = set of all rectangles.
Y ⊆ X, S ⊆ X, T ⊆ X, V ⊆ X, S ⊆ Y, S ⊆ T, V ⊆ T, Y ⊆ T, S ⊆ V.
(9) If M is any set, then write M ∪ Φ and M ∩ Φ.
M ∪ Φ = M. M ∩ Φ = Φ
(10*) Observe the Venn diagram and write the given sets U, A, B, A ∪ B and A ∩ B.
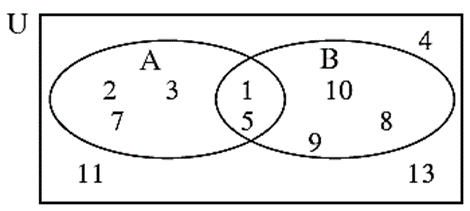
U = {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13}
A= {1, 2, 3, 5, 7}, B = {1, 5, 8, 9, 10},
A ∪ B = {1, 2, 3, 5, 7, 8, 9, 10}; A ∩ B = {1, 5}
(11) If n (A) = 7, n (B) = 13, n (A ∩ B) = 4, then n (A ∪ B} = ?
n(A ∪ B) = n(A) + n(B) — n(A ∩ B) …… (Rule)
= 7 + 13 — 4 …… (Substituting the given values)
= 20 — 4 = 16
∴ n(A ∪ B) = 16
(12) Fill in the blanks with elements of that set.
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1, 11, 13} B = {8, 5, 10, 11, 15} A’ = {........} B’ = {........}
A ∩ B = {............} A’ ∩ B’ = {...............}
A ∪ B = {............} A’ ∪ B’ = {............}
(A ∩ B)’ = {............} (A ∪ B)’ = {............}
Verify : (i) (A ∩ B)’ = A’ ∪ B’, (ii) (A ∪ B)’ = A’ ∩ B’
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1, 11, 13} B = {8, 5, 10, 11, 15} A’ = {3, 5, 8, 9, 10, 12, 15} B’ = {1, 3, 9, 12, 13}
A ∩ B = {11} ….(1)
A’ ∩ B’ = {3, 9, 12} …..(2)
A ∪ B = {1, 5, 8, 10, 11, 13, 15} ……(3)
A’ ∪ B’ = {1, 3, 5, 8, 9, 10, 12, 13, 15} ….(4)
(A ∩ B)’ = { 1, 3, 5, 8, 9, 10, 12, 13, 15} ……(5)
(A ∪ B)’ = { 3, 9, 12} ….(6)
Hence (i) From (4) and (5) (A ∩ B)’ = A’ ∪ B’,
(ii) From (6) and (2) (A ∪ B)’ = A’ ∩ B’
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 9th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Real Numbers – Online Solutions