Superposition of Waves
Maharashtra Board-Class-12th-Physics-Chapter-6
Notes-Part-1
|
Topics to be Learn : Part-1
|
Different types of waves : Water waves, sound waves, light waves, mechanical waves, electromagnetic waves etc.
Topics to be study in this chapter are mechanical waves, reflection of these waves, principle of superposition of waves, various phenomena like formation of stationary waves, beats, and their applications.
Mechanical wave : A mechanical wave is a wave motion in a material medium.
- Such a wave originates in the displacement of some portion of an elastic medium from its normal position.
- This causes the layers of matter to oscillate about their equilibrium positions. Because of the elastic properties of the material, the disturbance is transmitted from one layer to the next and so the waveform progresses through the medium.
Difference between mechanical waves and electromagnetic waves :
Mechanical waves
Electromagnetic waves
A mechanical wave is a wave motion in a material medium. Hence it needs for propagation a material medium which must be elastic and capable of storing energy, i.e., it must possess volume elasticity and inertia.
An electromagnetic wave does not need any material medium for propagation.
Progressive wave : A progressive wave or a wave motion is a periodic or oscillatory disturbance in a medium or in vacuum which is propagated without any damping and obstruction from one place to another at a finite speed. A progressive wave is also called a travelling wave.
Types of progressive wave: Progressive waves are of two types -transverse waves and longitudinal waves.
- Transverse progressive wave : A progressive wave in which the vibration of the individual particles of the medium is perpendicular to the direction of propagation of the wave is called a transverse progressive wave.
- Longitudinal progressive wave : A progressive wave in which the vibration of the individual particles of the medium is along the line of propagation of the wave is called a longitudinal progressive wave.
Simple harmonic progressive wave :
A simple harmonic progressive wave is a periodic disturbance in a medium or in vacuum which propagates at a finite speed and in which the vibrations of the particles of the medium, as in a mechanical wave, or the oscillations of the electric and magnetic fields as in an electromagnetic wave are simple harmonic.
Properties of progressive waves: 1) Each particle in a medium executes the same type of vibration. Particles vibrate about their mean positions performing simple harmonic motion. 2) All vibrating particles of the medium have the same amplitude, period and frequency. 3) The phase, (i.e., state of vibration of a particle), changes from one particle to another. 4) No particle remains permanently at rest. Each particle comes to rest momentarily while at the extreme positions of vibration. 5) The particles attain maximum velocity when they pass through their mean positions. 6) During the propagation of wave, energy is transferred along the wave. There is no transfer of matter. 7) The wave propagates through the medium with a certain velocity. This velocity depends upon properties of the medium. 8) Progressive waves are of two types : transverse and longitudinal. 9) A transverse wave can propagate only through solids, but not through liquids and gases while a longitudinal wave can propagate through any material medium.
Physical quantities related to a progressive wave :
Equation of a progressive wave travelling along the positive x-direction :
A progressive wave travelling along the positive x-direction is given by
y(x, t) = A sin (kx − ωt)
where A is the amplitude of the wave, k is the wave number and ω is the angular frequency.
[Note : y(x, t) = A sin (kx − ωt), y(x, t) = A sin (ωt − kx), y(x, t) = A cos (kx − ωt), y(x, t) = A cos (ωt − kx) also represent a progressive wave travelling in the positive x-direction. Hence, any one of them can be used y(x, t) can be written simply as y.]
Equation of a progressive wave travelling along the negative x-direction :
A progressive wave travelling along the negative x-direction is given by
y(x, t) = A sin (kx + ωt)
where A is the amplitude of the wave, k is the wave number and ω is the angular frequency.
Equation of a simple harmonic progressive wave in different forms : A simple progressive wave travelling along the positive x-direction is given by y=A sin (ωt−kx) ….(1) where A is the amplitude of the wave, k is the wave number and ω is the angular frequency. Wave number, k = \(\frac{2π}{λ}\) ∴ y = A sin (ωt − \(\frac{2π}{λ}x\)) …..(2) Angular frequency, ω = 2πn, Eq. (2) can be written as ∴ y = A sin (2πnt − \(\frac{2π}{λ}x\)) y = A sin 2π(nt − \(\frac{x}{λ}\)) …….(3) y = A sin 2πn(t − \(\frac{x}{nλ}\)) But nλ = v, the velocity of the wave. y = A sin 2πn(t − \(\frac{x}{v}\)) ……….(4) Also, writing n = v/λ in Eq. (3), we get, y = A sin \(\frac{2π}{λ}(vt − x)\) …… (5) Frequency of vibrations, n= 1/T Eq. (2) can be written as y = A sin \(2π(\frac{t}{T}-\frac{x}{λ})\) …… (6) Equations (1), (2), (3), (4), (5) and (6) are the different forms of the equation of a simple harmonic progressive wave.
Q. A simple harmonic progressive wave is given by y=A sin (ωt—kx), where the symbols have their usual meaning. What is (i) the particle velocity at a point x and time t (ii) the wave speed ?
(i) Particle velocity, \(\frac{dy}{dt}\) = ωA cos (ωt − kx) (ii) Wave speed, v = \(\frac{ω}{k}\)
Q. What is the minimum distance between any two particles of a medium which always have the same speed when a sinusoidal wave travels through the medium?
When a sinusoidal wave travels through a medium, the minimum distance between any two particles of the medium which always have the same speed is λ/2 Such particles are opposite in phase, i.e., their instantaneous velocities are opposite in direction. [Note : The minimum distance between any two particles which have the same velocity is λ]
Reflection of Waves:
When a progressive wave, travelling through a medium, reaches an interface separating two media, a certain part of the wave energy comes back in the same medium. The wave changes its direction of travel. This is called reflection of a wave from the interface.
The phenomenon in which a part of the wave is returned into the original medium with reduction in its intensity and energy is called reflection.
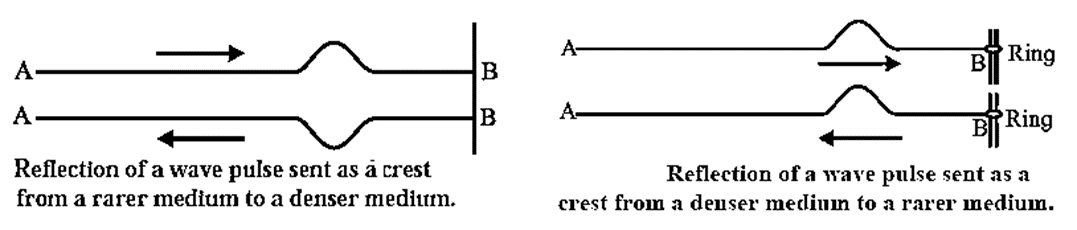
Reflection of transverse waves : Reflection of transverse waves from a denser medium : Suppose that a crest of a transverse wave travels along a string and is incident on the surface of a denser medium such as a rigid wall at point B, as shown in Fig. As the crest cannot travel further, it is reflected. Since point B is fixed, its displacement is always zero. Therefore, the crest must be reflected in such a way, that the displacement at B due to the reflected wave is exactly equal in magnitude and opposite in direction to that due to the incident wave. Therefore, the crest is reflected as a trough. Hence, there is a phase change of 180° or p radians when transverse waves are reflected from a denser medium. Reflection of transverse waves from rarer medium : In this case, the particles of the medium are free to vibrate. Hence, (i) there is no change of phase (ii) a crest is reflected as a crest and a trough is reflected as a trough.
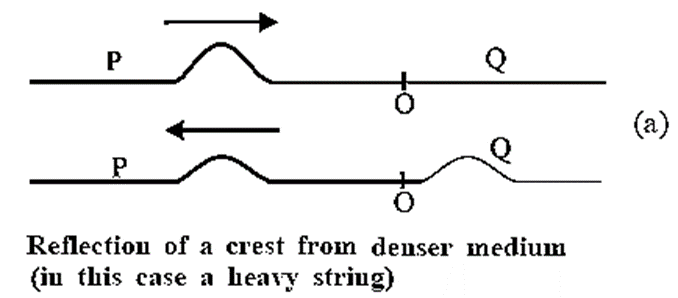
Q. Consider a heavy string P and a light string Q joined together at point O. Explain what happens when a wave pulse
(1) travelling from the string P reaches the junction O
(2) travelling from the string Q reaches the junction O.
The tension in both strings is the same. Hence, the junction O is a discontinuity between string P of greater linear density than string Q because the wave speed is less on P than on Q. (1) When a pulse travelling on the heavy string P reaches O, the light string Q gets pulled upwards. Thus the pulse, gets partially transmitted and partially reflected as a crest, as shown in Fig.(a) However, the amplitude of transmitted pulse is greater than that of the reflected pulse. (2) When a pulse travelling on a light string Q reaches O, the heavier string P pulled slightly upwards. Thus, the pulse is partly transmitted as a crest but the reflected part is inverted as a trough, as shown in Fig. (b). Here, the amplitude of transmitted pulse is smaller than that of the reflected pulse.
Reflection of sound waves :
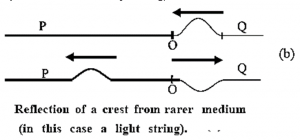
Reflection of a longitudinal wave from a denser medium :
Consider a sound wave incident on a denser medium such as a rigid wall. When a compression is incident on the wall, the particles of air close to the wall are in a compressed state.
To return to their normal condition, the particles begin to press in the opposite direction and therefore a compression gets reflected as a compression and a rarefaction is reflected as a rarefaction. There is no change of phase during this reflection (Fig.)
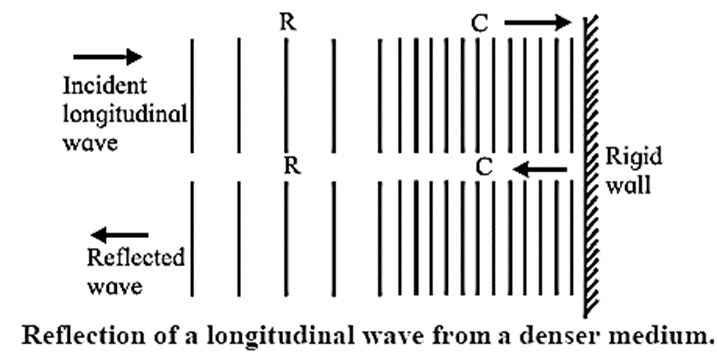
However, the displacements of the particles in the reflected wave are opposite to their displacements in the incident wave, so that there is a change of phase of 180° or p radians.
Reflection of a longitudinal wave from a rarer medium : When sound waves are reflected from the surface of a rarer medium, there is no change of phase. Therefore, a compression is reflected as a rarefaction and vice versa.
The reason is : When a compression is incident on the surface of a rarer medium, it can pass into that medium. This is because the particles of the rarer medimn are free to move and they get compressed, leaving a rarefaction behind, which travels in the opposite direction.
In a similar manner an incident rarefaction gets reflected as a compression.(Fig below)

Superposition of waves :
Principle of superposition of waves :
When two or more waves, travelling through a medium, pass through a common point, each wave produces its own displacement at that point, independent of the presence of the other wave.
The resultant displacement of a particle at a given point in space and time due to the simultaneous influence of two or more waves is the vector sum of the displacements due to each wave acting independently.
- The principle of superposition is applicable to all types of waves.
- The phenomena of interference, beats, formation of stationary waves, etc. are based on the principle of superposition of waves.
Let us consider superposition of two wave pulses in two different ways.
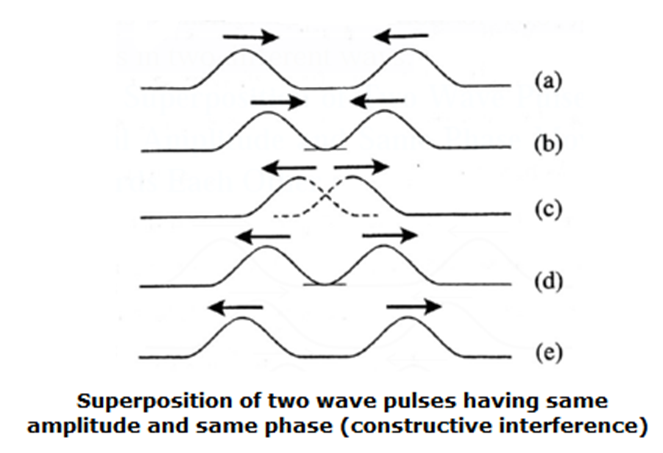
Superposition of Two Wave Pulses of Equal Amplitude and Same Phase Moving towards Each Other : Consider two wave pulses of the same amplitude and phase moving towards each other, as shown in Fig. When the two pulses cross each other, stages (b) to (d), the resultant displacement is equal to the vector sum of the displacements due to the individual pulses (shown by dashed lines). Therefore, the resultant displacement at that point becomes maximum. This phenomenon is called constructive interference. After crossing each other, both the pulses continue to propagate with their initial amplitude.
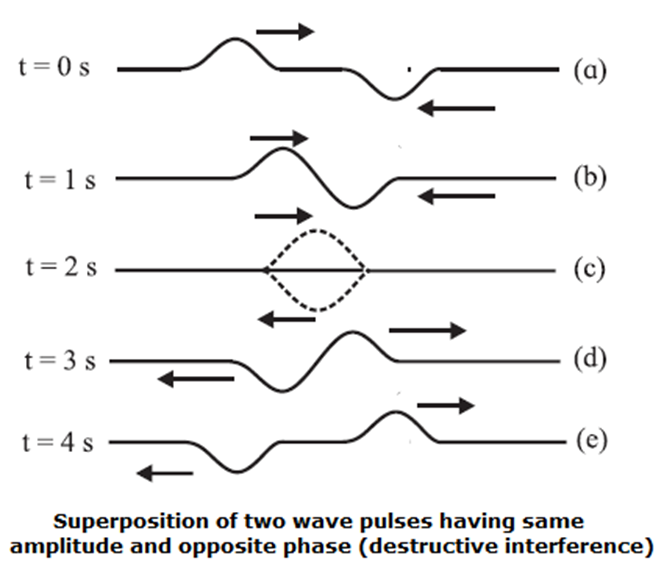
Superposition of Two Wave Pulses of Equal Amplitude and Opposite Phases Moving towards Each Other : Consider two wave pulses of the same amplitude but opposite phase moving towards each other, as shown in Fig. These wave pulses superimpose at t = 2 s and the resultant displacement (full line) is zero, due to individual displacements (dashed lines) differing in phase exactly by 180°. This is destructive interference. Displacement due to one wave pulse is cancelled by the displacement due to the other wave pulse when they cross each other (Fig. (c)). After crossing each other, both the wave pulses continue and maintain their individual shapes.
Music lovers often find many types of ambient sounds that interfere with the sounds coming through their headphones. Singers using a special type of headphones during recording of songs. Those are active noise cancellation headphones, which is the best possible solution to avoid background sound.
|
An equation for the resultant wave produced due to superposition of two waves : Consider two waves of the same frequency, different amplitudes A1 and A2 and differing in phase by φ. Let these two waves interfere at x = 0. The displacement of each wave at x = 0 are y1 = A1 sin ωt y2 = A2 sin (ωt + φ) According to the principle of superposition of waves, the resultant displacement at that point is y = y1 + y2 = A1 sin ωt + A2 sin (ωt + φ) Using the trigonometrical identity, sin (C+D) = sin C cos D + cos C sin D, y = A1 sin ωt+A2 ωt cos φ + A2 cos ωt sin φ y = (A1+A2 cos φ) sin ωt + A2 sin φ cos ωt ……(1) Let (A1+A2 cos φ) = A cos θ …..(2) And A2 sin φ = A sin θ ……(3) Substituting Eqs. (2) and (3) in Eq. (1), we get the equation of the resultant wave as y = A cos θ sin ωt + A sin θ cos ωt = A sin (ωt + θ) ...(4) It has the same frequency as that of the interfering waves. The amplitude A of the resultant wave is given by squaring and adding Eqs. (2) and (3) A2 cos2θ + A2 sin2θ = (A1+ A2 cos φ)2 + A22 sin2φ A2(cos2θ + sin2θ) = A12+ 2A1A2 cos φ + A22 cos2φ + A22 sin2φ ∴ A2 = A12+ 2A1A2 cos φ + A22(cos2φ + sin2φ) ∴ A = \(\sqrt{A_1^2+2A_1A_2 cos φ + A_2^2}\) …….(5)
Expression for the amplitude of the resultant wave when two waves are (1) in phase (2) out of phase : Case (1) :When the two interfering waves are in phase, φ = 0. Then, the amplitude of the resultant wave is A = \(\sqrt{A_1^2+2A_1A_2 cos 0 + A_2^2}\) ∴ A = \(\sqrt{A_1^2+2A_1A_2 + A_2^2}\) = \(\sqrt{(A_1 + A_2)^2}\) ∴ A = A1+ A2 ……(6) Thus, the amplitude of the resultant wave is maximum when the two interfering waves are in phase. Case (2) : When the two interfering waves are out of phase, φ = π. Then, the amplitude of the resultant wave is, A = \(\sqrt{A_1^2+2A_1A_2 cos π + A_2^2}\) ∴ A = \(\sqrt{A_1^2+2A_1A_2 (-1) + A_2^2}\) = \(\sqrt{(A_1 - A_2)^2}\) ∴ A = A1 − A2 ……(7) Thus, the amplitude of the resultant wave is minimum when the two interfering waves are in opposite phase. Intensity of the resultant wave : The intensities of the waves are proportional to the squares of their amplitudes. Hence, when φ = 0 Imin ∝ (Amin)2 where (Amin)2 = (A1 − A2)2 And when φ = π Imax ∝ (Amax)2 where (Amax)2 = (A1 + A2)2 Therefore intensity is maximum when the two waves interfere in phase while intensity is minimum when the two waves interfere out of phase.
Stationary wave :
When two progressive waves having the same amplitude, wavelength and speed, travel through the same region of a medium in opposite directions, their super-position under certain conditions creates a stationary interference pattern called as a stationary OR standing wave.
It is called stationary because the resultant harmonic disturbance of the particles does not travel in any direction and there is no transport of energy in the medium.
Expression for the equation of a stationary wave on a stretched string : When two progressive waves having the same amplitude, wavelength and speed propagate in opposite directions through the same region of a medium, their superposition under certain conditions creates a stationary interference pattern called a stationary wave. Consider two simple harmonic progressive waves, of the same amplitude A, wavelength λ and frequency n = ω/2π, travelling on a string stretched along the x-axis in opposite directions. They may be represented by y1 = A sin (ωt − kx) (along the + x-axis) and ….(1) y2 = A sin (ωt + kx) (along the — x-axis) …..(2) where k = 2π/λ is the propagation constant. By the superposition principle, the resultant displacement of the particle of the medium at the point at which the two Waves arrive simultaneously is the algebraic sum y = y1 + y2 = A[sin (ωt − kx) + sin (ωt + kx)] Using the trigonometrical identity, Sin C + sin D = 2 sin\((\frac{C−D}{2})\) cos\((\frac{C−D}{2})\) y = 2A sin ωt cos (−kx) = 2A sin ωt cos kx ….[… cos (−kx) = cos (kx)] = 2A cos kx sin ωt ….(3) y = R sin ωt, ...(4) where R = 2A cos kx. ….(5) Equation (4) is the equation of a stationary wave.
Stationary nature: The above equation shows that the resultant disturbance is simple harmonic having the same period as that of the individual waves and the amplitude |R|. R varies periodically with the position x.
The absence of the term, ± kx in the sine function implies the stationary nature, i.e., the resultant disturbance does not propagate along the positive or negative x—axis. It follows that there is no energy transport in the medium. Hence, it is called a stationary wave or a standing wave.
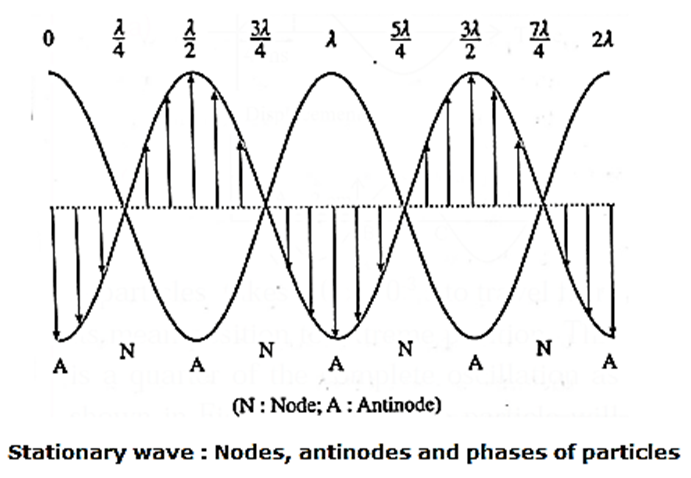
The absence of the term in t in the cosine function shows that each particle vibrates with a fixed amplitude that varies only with the location (x) of the particle.
Nodes and antinodes : Nodes are the points of minimum displacement. This is possible if the amplitude is minimum (zero), At nodes, R = 0. ∴ cos \(\frac{2πx}{λ}\) = 0 …(.. A ≠ 0 and k = \(\frac{2π}{λ}\) ) \(\frac{2πx}{λ}=\frac{π}{2}=\frac{3π}{2}=\frac{5π}{2}\) ∴ x = \(\frac{λ}{4}=\frac{3λ}{4}=\frac{5λ}{4}\)….. (2p+1) \(\frac{λ}{4}\) ....(1) where p =0, 1, 2, …. Therefore, the distance between successive nodes is [2(p+1) + 1]\(\frac{λ}{4}\) − (2p+1)\(\frac{λ}{4}\) = \(\frac{λ}{2}\) The points at which the particles of the medium vibrate with the maximum amplitude are called the antinodes. At antinodes, R = ± 2A ∴ cos \(\frac{2πx}{λ}\)= ± 1 ∴ \(\frac{2πx}{λ}\) = 0, π, 2π, 3π …… ∴ x = 0, \(\frac{λ}{2}\), λ, \(\frac{3λ}{2}\) .... \(\frac{pλ}{2}\) …. (p = 0,1, 2, 3…..) …. (2) Therefore, the distance between successive antinodes is \(\frac{(p+1)λ}{2}\) − \(\frac{pλ}{2}\) = \(\frac{λ}{2}\) ∴ Distance between successive nodes = distance between successive antinodes = \(\frac{λ}{2}\). From Eqs. (1) and (2), it can be seen that (i) the nodes and the antinodes occur alternately and are equally spaced (ii) the distance between a node and an adjacent antinode =\(\frac{(2p+1)λ}{4}\) − \(\frac{pλ}{2}\) =\(\frac{(2p+1)λ}{4}\) − \(\frac{2pλ}{4}\) = \(\frac{λ}{4}\)
Transverse stationary wave : When two identical transverse progressive waves travelling in opposite directions along the same line superimpose, the resultant wave produced is called a transverse stationary wave.
Longitudinal stationary wave : When two identical longitudinal progressive waves superimpose, the resultant wave produced is called a longitudinal stationary wave.
Properties of Stationary Waves: Since the nodes are points where the particles are always at rest, energy cannot be transmitted across a node. The energy of the particles within a loop remains localized, but alternates twice between kinetic and potential energy during each complete vibration. When all the particles are in the mean position, the energy is entirely kinetic. When they are in their extreme positions, the energy is entirely potential.
Distinguish between progressive waves and stationary waves :
Progressive waves
Stationary waves
They are produced when a disturbance is created in the medium.
They are produced due to interference, under certain conditions, between two identical progressive waves travelling in opposite directions.
They continuously travel away from the source and transport energy through the medium.
They do not move in any direction and hence do not transport energy through the medium.
Every particle vibrates with the same amplitude.
Amplitude of vibration is different for different particles.
Phase changes from particle to particle.
All the particles in the same loop have the same phase, while the particles in adjacent loops are in opposite phase.
Every particle of the medium is set into vibrations by these waves.
There are some particles of the medium which do not vibrate at all.
Free and forced vibrations :
The frequency at which an object tends to vibrate when hit, plucked or somehow disturbed is known as its natural frequency. In these vibrations, object is not under the influence of any outside force.
- If a simple pendulum is pulled aside and released, it oscillates freely about its equilibrium position at its natural frequency which is inversely proportional to the square root of its length and directly proportional to the square root of the acceleration of gravity at the place. These oscillations, called as free oscillations, are periodic and tautochronous if the displacement of its bob is small and the dissipative forces can be ignored.
- When a guitar string is plucked, two wave pulses of the same amplitude, frequency and phase move out from that point towards the fixed ends of the string where they get reflected. For certain ratios of wavelength to length of the string, these reflected pulses moving towards each other will meet in phase to form standing waves on the string. The vibrations of the string cause the air molecules to oscillate, forming sound waves that radiate away from the string. The frequency of the sound waves is equal to the frequency of the vibrating string. In general, the wavelengths of the sound waves and the waves on the string are different because their speeds in the two mediums are not the same.
Free vibrations ; A body capable of vibrations is said to perform free vibrations when it is disturbed from its equilibrium position and left to itself. i.e. In free vibration, the body at first is given an initial displacement and the force is then withdrawn. The body starts vibrating and continues the motion on its own. No external force acts on the body further to keep it in motion.
Forced vibrations : The vibrations of a body in response to an external periodic force are called forced vibrations.
Resonance : If a body is made to vibrate by an external periodic force, whose frequency is equal to the natural frequency (or nearly so) of the body, the body vibrates with maximum amplitude. This phenomenon is called resonance.
The corresponding frequency is called the resonant frequency.

For low damping, the amplitude of vibrations has a sharp maximum at resonance, as shown in Fig. The flatter curve without a pronounced maximum is for high damping.
Applications of resonance :
Disadvantages of resonance :
Download PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Text Book Get PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Notes Get PDF from store : Class-12-Physics-Chapter-6-Superposition of Waves–Solution
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-5-Oscillations –Online Solution Next Chapter : Chapter-7- Wave Optics – Online Solution
We reply to valid query.