Thermodynamics
Maharashtra Board-Class-12th-Physics-Chapter-4
Solutions
Question 1.
Choose the correct option.
i) A gas in a closed container is heated with 10J of energy, causing the lid of the container to rise 2m with 3N of force. What is the total change in energy of the system?
(A) 10J (B) 4J
(C) -10J (D) - 4J
(B) 4J
ii) Which of the following is an example of the first law of thermodynamics?
(A) The specific heat of an object explains how easily it changes temperatures.
(B)While melting, an ice cube remains at the same temperature.
(C) When a refrigerator is unplugged, everything inside of it returns to room temperature after some time.
(D) After falling down the hill, a ball's kinetic energy plus heat energy equals the initial potential energy.
(B) While melting, an ice cube remains at the same temperature. [Here, ∆u = 0, W = Q]
(C) When a refrigerator is unplugged, everything inside of it returns to room temperature after some time.
(D) After falling down the hill, a ball’s kinetic energy plus heat energy equals the initial potential energy.
iii) Efficiency of a Carnot engine is large when
(A) TH is large (B) TC is low
(C) TH - TC is large (D) TH - TC is small
(A) TH is large
(B) TC is low
(C) TH – TC is large
[ η = \(\frac{T_H-T_C}{T_H}=1-\frac{T_C}{T_H}\), ]
iv) The second law of thermodynamics deals with transfer of:
(A) work done (B) energy
(C) momentum (D) heat
(B) energy
v) During refrigeration cycle, heat is rejected by the refrigerant in the :
(A) condenser (B) cold chamber
(C) evaporator (D) hot chamber
closed tube [refer the textbook]
Question 2.
Answer in brief.
i) A gas contained in a cylinder surrounded by a thick layer of insulating material is quickly compressed. (a) Has there been a transfer of heat? (b) Has work been done?
If a gas contained in a cylinder surrounded by a thick layer of insulating material is quickly compressed then (a) There is no transfer of heat. (b) The work is done on the gas
ii) Give an example of some familiar process in which no heat is added to or removed form a system, but the temperature of the system changes.
Hot water in a container cools after sometime. Its temperature goes on decreasing with time and after sometime it attains room temperature. Note ; Here, we do not provide heat to the water or remove heat from the water. The water cools on exchange of heat with the surroundings.
iii) Give an example of some familiar process in which heat is added to an object, without changing its temperature.
(a) Melting of ice (b) Boiling of water
iv) What sets the limits on efficiency of a heat engine?
The temperature of the cold reservoir sets the limit on the efficiency of a heat engine. [Note: η = \(1-\frac{T_C}{T_H}\) This formula shows that for maximum efficiency, TC should be as low as possible and TH should be as high as possible.] For a Carnot engine, efficiency η = \(1-\frac{T_C}{T_H}\), η →1 as TC → 0
v) Why should a Carnot cycle have two isothermal two adiabatic processes?
With two isothermal and two adiabatic processes all reversible, the efficiency of the Carnot engine depends only on the temperatures of the hot and cold reservoirs. Thus, the cycle includes two isothermal and two adiabatic processes for maximum efficiency.
Question 3.
i) A mixture of hydrogen and oxygen is enclosed in a rigid insulting cylinder. It is ignited by a spark. The temperature and the pressure both increase considerably.
Assume that the energy supplied by the spark is negligible, what conclusions may be drawn by application of the first law of thermodynamics?
The internal energy of a system is the sum of potential energy and kinetic energy of all the constituents of the system. In the example stated above, conversion of potential energy into kinetic energy is responsible for a considerable rise in pressure and temperature of the mixture of hydrogen and oxygen ignited by the spark.
ii) A resistor held in running water carries electric current. Treat the resistor as the system (a) Does heat flow into the resistor? (b) Is there a flow of heat into the water? (c) Is any work done? (d) Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
(a) Heat is generated into the resistor due to the passage of electric current. In the usual notation, heat generated = I2Rt. (b) Yes. Water receives heat from the resistor. (c) I2Rt = MCΔT + PΔV (Q) (ΔU) (W) Here, I = current through the resistor, R = resistance of the resistor, t = time for which the current is passed through the resistor, M=mass of the water, S =specific heat of water, T=rise in the temperature of water, P = pressure against which the work is done by the water, ΔU = increase in the volume of the water.
iii) A mixture of fuel and oxygen is burned in a constant-volume chamber surrounded by a water bath. It was noticed that the temperature of water is increased during the process. Treating the mixture of fuel and oxygen as the system, (a) Has heat been transferred ? (b) Has work been done? (c) What is the sign of ΔU ?
(a) Heat has been transferred from the chamber to the water bath. (b) No work is done by the system (the mixture of fuel and oxygen) as there is no change in its volume. (c) There is increase in the temperature of water. Therefore, ΔU is positive for water. For the system (the mixture of fuel and oxygen), ΔU is negative.
iv) Draw a p-V diagram and explain the concept of positive and negative work. Give one example each.
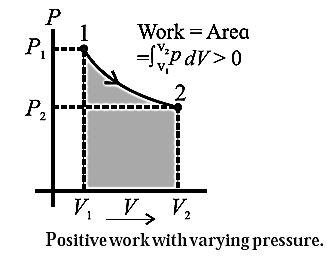
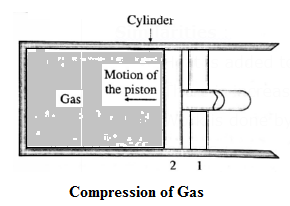
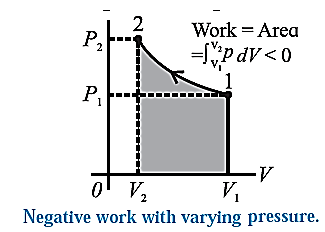
Consider some quantity of an ideal gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. See Fig.. Suppose the gas is allowed to expand by moving the piston outward extremely slowly. There is decrease in pressure of the gas as the volume of the gas increases. Figure shows the corresponding p— V diagram. In this case, the work done by the gas on its surroundings, W =\( \int_{V_1}^{V_2}PdV\) (= area under the curve) is positive as the volume of the gas has increased from V1 to V2. Let us now suppose that starting from the same initial condition, the piston is moved inward extremely slowly so that the gas is compressed. There is increase in pressure of the gas as the volume of the gas decreases. Below figure shows the corresponding p—V diagram. In this case, the work done by the gas on its surroundings, W = \( \int_{V_1}^{V_2}PdV\) ( = area under the curve) is negative as the volume of the gas has decreased from V1 to V2 .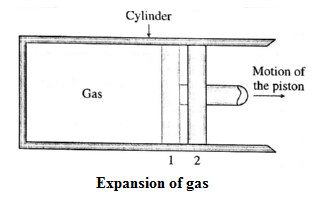
v) A solar cooker and a pressure cooker both are used to cook food. Treating them as thermodynamic systems, discuss the similarities and differences between them.
Similarities : Differences : Note ; A solar cooker can be used only when enough solar radiation is available
Question 4.
A gas contained in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 5 litres to a volume of 10 litres. In doing so it absorbs 400 J of thermal energy from its surroundings.
Determine the change in internal energy of system.
Data: P = 1 atm = 1.013 x 105 Pa, V1 =5 litres =5 x 10-3 m3, V2 = 10 Litres = 10 x 10-3 m3, Q = 400J. The work done by the system (gas in this case) on its surroundings, W = P (V2 − V1) = (1.013 x 105) (10 x 10-3 − 5 x 10-3) = 1.013 (5 x 102)] = 5.065 x 102J The change in the internal energy of the system, ΔU = Q − W = 400 − 506.5 = −106.5J The minus sign shows that there is a decrease in the internal energy of the system.
Question 5.
A system releases 125 kJ of heat while 104 kJ of work is done on the system. Calculate the change in internal energy.
Given: Q = −125kJ, W= −104kJ ΔU = Q − W= −125−(−104) = (−125 + 104) = −21kJ. Negative sign shows that decrease in energy. This is the change (decrease) in the internal energy.
Question 6.
Efficiency of a Carnot cycle is 75%. If temperature of the hot reservoir is 727ºC, calculate the temperature of the cold reservoir.
Given : η = 75% = 0.75, TH = (273 + 727) K = 1000 K η = \(1−\frac{T_C}{T_H}\) ∴ \frac{T_C}{T_H}= 1− η TC = TH (1 − η ) = 1000(1 - 0.75) = 250 K = (250 − 273)°C = −23°C This is the temperature of the cold reservoir.
Question 7.
A Carnot refrigerator operates between 250ºK and 300ºK. Calculate its coefficient of performance.
Given : TC = 250 K, TH = 300 K
K = \(\frac{T_C}{T_H-T_C}=\frac{250}{300-250}=\frac{250}{50}\) = 5
this is the coefficient of performance of the refrigerator.
Question 8.
An ideal gas is taken through an isothermal process. If it does 2000 J of work on its environment, how much heat is added to it?
Given : W = 2000J , isothermal process In this case, the change in the internal energy of the gas, ΔU=0, as the gas is taken through an isothermal process. Hence, the heat added to it, Q = ΔU + W = 0 + W = 2000J (Note : For an isothermal process, none of the quantities Q and W is zero.)
Question 9.
An ideal monatomic gas is adiabatically compressed so that its final temperature is twice its initial temperature. What is the ratio of the final pressure to its initial pressure?
Given : Tf = 2Ti, monatomic gas ϒ = 5/3 PiViϒ = PfVfϒ in an adiabatic process Now, PV= nRT ∴ V = nRT/P ∴ Vi = \(\frac{nRT_i}{P_i}\) and Vf = \(\frac{nRT_f}{P_f}\) ∴ \(P_i(\frac{nRT_i}{P_i})^\gamma = P_f(\frac{nRT_f}{P_f})^\gamma\) ∴ Pi1−ϒTiϒ = Pf1−ϒTfϒ ∴ \((\frac{T_f}{T_i})^{\gamma}\) = \((\frac{P_i}{P_f})^{1-\gamma}\) ∴ \((\frac{T_f}{T_i})^{\gamma}\) = \((\frac{P_f}{P_i})^{\gamma -1}\) ∴ \(2^\frac{5}{3} = (\frac{P_f}{P_i})^{\frac{5}{3}-1} = (\frac{P_f}{P_i})^{\frac{2}{3}}\) ∴ \(\frac{5}{3}log\,2=\frac{2}{3}log(\frac{P_f}{p_i})\) ∴ \(\frac{5}{3}0.3010=\frac{2}{3}log(\frac{P_f}{p_i})\) ∴ \((2.5)(0.3010)=log(\frac{P_f}{p_i})\) ∴ 0.7525 = \(log(\frac{P_f}{p_i})\) = \((\frac{P_f}{p_i})\) = antilog (0.7525) = 5.656 This is ratio of final pressure to its initial pressure
Question 10.
A hypothetical thermodynamic cycle is shown in the figure. Calculate the work done in 25 cycles.
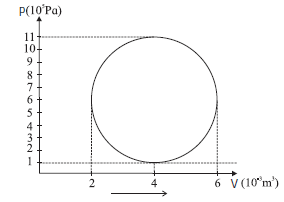
Given : a = \(\frac{ΔV_{max}}{2}=\frac{6-2}{2}×10^{-3}m^3\) = 2 x 10−3 m3, b = \(\frac{ΔP_{max}}{2}=\frac{11-1}{2}×10^{5}Pa\) = 5 x 105 Pa Cycles = 25 The work done in one cycle, \(\oint PdV\) = πab = (3.142) (2 x 10−3) (5 x 105) = 3.142 x 103J Hence, the work done in 25 cycles = (25) (3.142 x 103) = 7.855 x 104J This is the work done in 25 cycles
Question 11.
The figure shows the V-T diagram for one cycle of a hypothetical heat engine which uses the ideal gas. Draw (a) the p-V diagram and p-T diagram of the system.
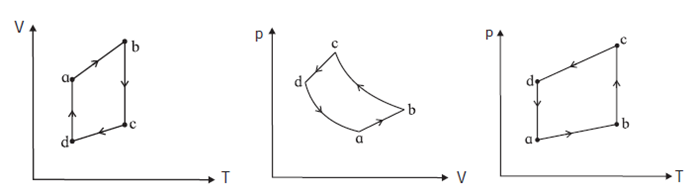
(a) P—- V diagram (Schematic): ab : isobaric process, bc : isothermal process, cd : isobaric process, da : isothermal process. \(\frac{P_aV_a}{T_a}=\frac{P_bV_b}{T_b}=\frac{P_cV_c}{T_c}=\frac{P_dV_d}{T_d}\)= nR (b) P—T diagram (Schematic) :

Question 12.
A system is taken to its final state from initial state in hypothetical paths as shown figure calculate the work done in each case.
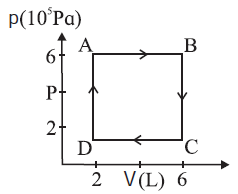
Given : PA = PB = 6 x 105 Pa, PC = PD= 2 x 105 Pa VA = VD = 2 L, VB = VC = 6 L, 1 L=10−3 m3 (i) The work done along the path A —> B (isobaric process), WAB = PA (VB − VA) = (6 x 105) (6 − 2) (10-3) = 2.4 x 103J (ii) WBC = zero as the process is isochoric (V = constant). (iii) The work done along the path C —> D (isobaric process), WCD = PC (VD− Vc) = (2 x 105 Pa) (2 − 6) (10-3) = −8 x 102J (iv) WDA = zero as V = constant.
Download PDF from store : Chapter-4-Thermodynamics-Text Book Get PDF from store : Chapter-4-Thermodynamics-Notes Get PDF from store : Chapter-4-Thermodynamics-Solution
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-3-Kinetic Theory of Gases and Radiations –Online Solution Next Chapter : Chapter-5-Oscillations – Online Solution
We reply to valid query.