Notes-Part-2
Topics to be Learn : Part-2
|
Energy of a Particle Performing S.H.M.:
While performing an S.H.M., the particle possesses speed (hence kinetic energy) at all the positions except at the extreme positions.
In spite of the presence of a restoring force (except at the mean position), the particle occupies various positions. This is an indication that work is done and the system has potential energy (elastic - in the case of a spring, gravitational - for a pendulum, magnetic - for a magnet, etc.).
Total energy of the particle performing an S.H.M. is thus the sum of its kinetic and potential energies.
Consider a particle of mass m performing linear SHM with amplitude A. The restoring force acting on the particle is P = −kx, where k is the force constant and x is the displacement of the particle from its mean position.
Kinetic energy : At distance x from the mean position, the velocity is v = \(ω\sqrt{A^2−x^2}\) where ω = \sqrt{\frac{k}{m}}\) . The kinetic energy (KE) of the particle is KE = ½ mv2 = ½ mω2(A2 − x2) = ½ k(A2 − x2) ……..(1) If the phase of the particle at an instant t is 0 = ωt + α, where a is initial phase, its velocity at that instant is v = ωA cos (ωt + α) and its KE at that instant is KE = ½ mv2 = ½ mω2A2 cos2(ωt + α) = ½ kA2 cos2(ωt + α) …..(2) Therefore, the KE varies with time as cos2θ .
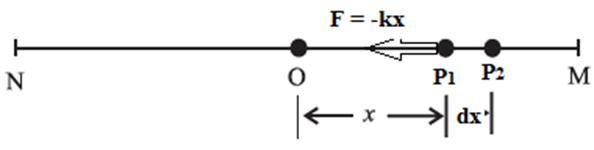
Potential energy : The potential energy of a particle in linear SHM is defined as the work done by an external agent, against the restoring force, in taking the particle from its mean position to a given point in the path, keeping the particle in equilibrium. Suppose the particle in fig. is displaced from P1 to P2, through an infinitesimal distance dx against the restoring force F as shown. The corresponding work done by the external agent will be dW = (- F )dx = kx dx. This work done is stored in the form of potential energy. The potential energy (PE) of the particle when its displacement from the mean position is x can be found by integrating the above expression from 0 to x. ∴ PE = \(\int dW =\int kx\,dx =\frac{1}{2}dx^2 \) The displacement of the particle at an instant t being P x = A sin (ωt + α) its PE at that instant is PE = ½ kx2 = ½ kA2 sin (ωt + α) …….(4) Therefore, the PE varies with time as sin2θ.
Total energy : The total energy of the particle is equal to the sum of its potential energy and kinetic energy. From Eqs. (1) and (2), total energy is E = PE + KE = ½ kx2 + ½ k(A2 – x2) = ½ kx2 + ½ kA2 – ½ k x2 = ½ kA2 = ½ mω2A2 = …….(5) Total energy of SHM in terms of acceleration is E = ½ mω2A2 = ½ mAamax (….amax = ω2A) ∴ E = ½ mAamax is the the expression of total energy in terms of acceleration. As m is constant, and ω and A are constants of the motion, the total energy of the particle remains constant (or its conserved).
Factors on which the total energy of a particle executing SHM depends :
If η is the frequency in S.H.M. ω = 2πη and for T is the period of the motion w = 2π/T
Using this in Eq. (5), we get
= 2π2mη2A2 = \(\frac{2π^2mA^2}{T^2}\)
Conclusions :The total energy of the particle is
- independent of x and thus remains constant when m, w and A are constant,
- directly proportional to the force constant (E ∝ k),
- directly proportional to the mass of the particle (E ∝ m),
- directly proportional to the square of the amplitude (E ∝ A2),
- proportional to the square of the frequency η (E ∝ η2 ),
- inversely proportional to the square of the period T (E ∝ 1/T2).
Expressions for the kinetic energy and potential energy of a particle performing SHM at (i) an extreme position (ii) the mean position : For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency w= , its kinetic and potential energies are respectively, KE = ½ k(A2−x2) PE = ½ kx2 and total energy, E = ½ kA2 (i) At the mean position, x = 0, KE = ½ kA2 = E and PE=0 (ii) At an extreme position, x = ±A KE = 0 and PE = ½ kA2 = E That is, the energy transfers back and forth between kinetic energy and potential energy, while the total mechanical energy of the oscillating particle remains constant. The total energy is entirely kinetic energy at the mean position and entirely potential energy at the extremes.
Special cases:
Expressions for the kinetic energy (KE) and potential energy (PE) at a displacement x for a particle performing linear SHM.
(i) the displacement at which KE is equal to PE
(ii) the KE and PE when the particle is halfway to a extreme position. :
For a particle of mass m executing SHM with force constant k, amplitude A and angular frequency w = , its kinetic and potential energies are respectively,
KE = ½ k(A2−x2)
PE = ½ kx2
and total energy, E = ½ kA2
(i) For PE = KE
½ kx2 = ½ k(A2−x2)
∴ 2x2 = A2 , ∴ x = ± \(\frac{A}{\sqrt{2}}\)
∴ At x = ± \(\frac{A}{\sqrt{2}}\)
PE = ½ kx2 = ½ (½kA2)
KE = ½ k(A2−A2/2) = ½(½kA2)
∴ PE = KE = ½ E
(ii) At x = ± \(\frac{A}{2}\)
PE = ½(¼kA2) = ¼ (½kA2) = ¼ E
and KE = ½ k(A2−A2/4) = ½ (¾kA2) = ¾(½kA2) = ¾ E
At x= ± \(\frac{A}{2}\, the energy is 25% potential energy and 75% kinetic energy.
Ratio of PE to KE for x = A/2 :
At x= A/2 , PE = ¼(½kA2) and KE = ¾ (½kA2)
∴ PE/KE = 1/3 is the required ratio.
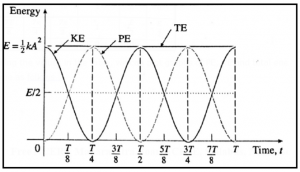
Graphical representation of the variation of K.E. and P.E. with displacement in S.H.M :
The variation of K.E. and P.E. with displacement in S.H.M. is shown in Fig.
Graphical representation of the variation of potential energy, kinetic energy and total energy of a particle performing SHM with time. Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position; ω = \(\sqrt{k/m} is the appropriate constant related to the system. The total energy of the particle is E= ½kA2 Its displacement (x), potential energy (PE) and kinetic energy (KE) at any instant are given by x = A sin ωt PE = ½ kx2 = ½ kA2 sin2ωt = E/2(1 − cos2ωt) KE = ½ k(A2 − x2) = E − PE Using the values in the table, we can plot graphs of PE, KE and total energy with time as follows :
Simple Pendulum: An ideal simple pendulum is a heavy particle suspended by a massless, inextensible, flexible string from a rigid support.
A practical simple pendulum is a small heavy (dense) sphere (called bob) suspended by a light and inextensible string from a rigid support.
Consider a simple pendulum of length L, suspended from a rigid support O. When displaced from its initial position of rest through a small angle q in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in Fig.
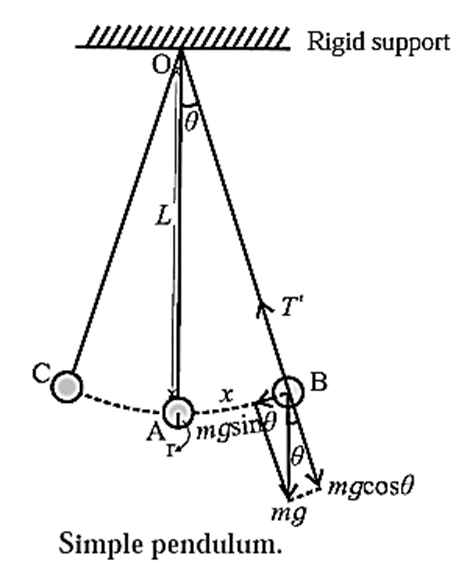
Expression for the period of a simple pendulum : At B, the forces on the bob are its weight mg and the tension T’ in the string. Resolve mg into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string. mg cos θ is balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position. Restoring force, F = − mg sin θ If θ is small and expressed in radian, sin θ » θ = \(\frac{arc}{radius}=\frac{AB}{OB} =\frac{x}{L}\) ∴ F = − mgθ = − mg\(\frac{x}{L}\) ….(1) Since m, g and L are constant, ∴ F ∝ (−x) …….(2) Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM. Acceleration, a = F/m = \(\frac{g}{L}x\) ......(3) Therefore, acceleration per unit displacement \(\left | \frac{a}{x} \right |=\frac{g}{L} \) Period of SHM, T = \(\frac{2π}{\sqrt{\text{acceleration per unit displacement}}}=\frac{2π}{\sqrt{g/L}}\) ∴ T = \(2π\sqrt{L/g}\) This gives the expression for the period of a simple pendulum.
The oscillations of a simple pendulum are approximately linear simple harmonic only if
- the amplitude of oscillation is very small compared to its length
- the oscillations are in a single vertical plane.
Laws of a simple pendulum : The period of a simple pendulum at a given place is T = \(2π\sqrt{L/g}\) where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows Law of length :The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length. T ∝ \(\sqrt{L}\) Law of mass :The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum. Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity. T ∝ \(\sqrt{\frac{1}{g}}\) Law of isochronism :The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small.
Expression for the angular frequency of a body performing linear SHM : When a body of mass m performs linear SHM, the restoring force on it is always directed towards the mean position and its magnitude is directly proportional to the magnitude of the displacement of the body from the mean position. Thus, if F is the force acting on the body when its displacement from the mean position is x, F = ma = — kx where the constant k, the force per unit displacement, is called the force constant. Let k/m = ω2, a constant. ∴ Acceleration, a = \(−\frac{k}{m}x\) = − ω2x The angular frequency, ω = \(\sqrt{k/m}\) = \(\sqrt{\left | \frac{a}{x} \right |}\) ∴ ω = \(\sqrt{\text{acceleration per unit displacement}}\)
Second’s Pendulum: A simple pendulum whose period is two seconds is called second’s pendulum.
The period of a simple pendulum at a given place is
T = \(2π\sqrt{L/g}\)
For a second's pendulum, T= 2 s
2 = \(2π\sqrt{L_s/g}\) ….(1)
where Ls is the length of second’s pendulum, having period T = 2s.
∴ LS = g/π2
At a given place, the value of g is constant.
LS = g/π2 = a fixed value, at a given place
Using this relation, we can find the length of a second’s pendulum at a place, if we know the acceleration due to gravity at that place.
Experimentally, if LS is known, it can be used to determine acceleration due to gravity g at that place.
Distinguish between a simple pendulum and a conical pendulum :
Angular S.H.M. and its Differential Equation:
Below figure shows a metallic disc attached centrally to a thin wire, hanging from a rigid support.
If the disc is slightly twisted about the axis along the wire, and released, it performs rotational motion partly in clockwise and anticlockwise (or opposite) sense. Such oscillations are called angular oscillations or torsional oscillations.
Suppose a disc is suspended from its centre by a wire or a twistless thread such that the disc remains horizontal, as shown in below Fig.
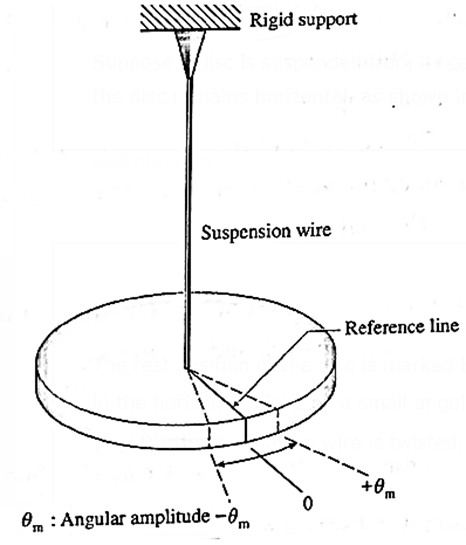
The rest position of the disc is marked by a reference line. When the disc is rotated in the horizontal plane by a small angular displacement θ = θm, from its rest position (θ = θ), the suspension wire is twisted. When the disc is released, it oscillates about the rest position in angular or torsional oscillation with angular amplitude θm.
The device is called a torsional pendulum and the springiness or elasticity of the motion is associated with the twisting of the suspension wire. The twist in either direction stores potential energy in the wire and provides an alternating restoring torque, opposite in direction to the angular displacement.
The motion is governed by this torque. If the magnitude of the restoring torque (τ) is proportional to the angular displacement (θ),
τ ∝ (−θ) or τ = −cθ ...(1)
where the constant of proportionality c is called the torsion constant, that depends on the length, diameter and material of the suspension wire. In this case, the oscillations will be simple harmonic.
Let I be the moment of inertia (MI) of the oscillating disc.
Torque = MI x angular acceleration
τ = Iα = \(I\frac{d^2θ}{dt^2}\)
From eq (1)
\(I\frac{d^2θ}{dt^2}\) = −cθ
∴ \(I\frac{d^2θ}{dt^2}\) + −cθ = 0
This is the differential equation of angular SHM.
Angular displacement being a dimensionless quantity, the SI unit of torsion constant is the same as that of torque = the newton-metre (N-m)
Expression for the period of angular SHM in terms of (i) the torsion constant (ii) the angular acceleration. Definition : Angular SHM is defined as the oscillatory, motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement. The differential equation of angular SHM is \(I\frac{d^2θ}{dt^2}\) + −cθ = 0 …. (1) where I = moment of inertia of the oscillating body, \(\frac{d^2θ}{dt^2}\)= angular acceleration of the body when its angular displacement is q, and c = torsion constant of the suspension wire, \(\frac{d^2θ}{dt^2}+\frac{c}{I}θ\) = 0 Let c/I = ω2, a constant. Therefore, the angular frequency, ω = \(\sqrt{c/I}\) and the angular acceleration, a = \(\frac{d^2θ}{dt^2}\) = − ω2θ …. (2) The minus sign shows that the a and θ have opposite directions. The period T of angular SHM is T = 2π/ω = \(\frac{2π}{\sqrt{c/I}} = 2π\sqrt{\frac Ic}\) …. (3) This is the expression for the period in terms of torque constant. Also, from Eq. (2), ω =\(\sqrt{\left | \frac{α}{θ} \right |}\) = \(\sqrt{\text{angular acceleration per unit angular displacement}}\) ∴T = 2π/ω = \(\frac{2π}{\sqrt{α/θ}}=\frac{2π}{\sqrt{\text{angular acceleration per unit angular displacement}}}\)
Magnet Vibrating in Uniform Magnetic Field: If a bar magnet is freely suspended in the plane of a uniform magnetic field, it remains in equilibrium with its axis parallel to the direction of the field. If it is given a small angular displacement θ (about an axis passing through its centre, perpendicular to itself and to the field) and released, it performs angular oscillations Fig.
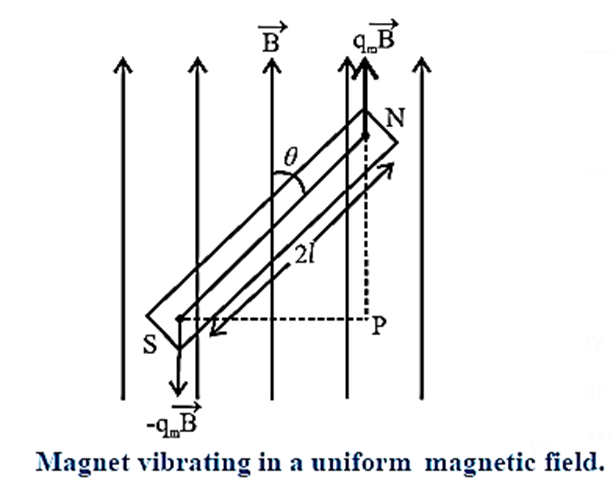
Consider a bar magnet of magnetic moment μ, suspended horizontally by a light twistless fibre in a region where the horizontal component of the Earth's magnetic field is B. The bar magnet is free to rotate in a horizontal plane. It comes to rest in approximately the North—South direction, along B.
If it is rotated in the horizontal plane by a small displacement θ from its rest position (θ =0),the suspension fibre is twisted. When the magnet is released, it oscillates about the rest position in angular or torsional oscillation.
The bar magnet experiences a torque r due to the field B. Which tends to restore it to its original orientation parallel to B. For small θ, this restoring torque is
τ = −μB sin θ = −μBθ ...(1)
where the minus sign indicates that the torque is opposite in direction to the angular displacement θ.
Equation (1) shows that the torque (and hence the angular acceleration) is directly proportional in magnitude of the angular displacement but opposite in direction. Hence, for small angular displacment, the oscillations of the bar magnet in a uniform magnetic field is simple harmonic.
Expression for the period of a magnet in angular simple harmonic oscillations in a uniform magnetic field : For clockwise angular displacement θ , the restoring torque is in the anticlockwise direction. ∴ τ = Iα = −μBθ where I is the moment of inertia of the bar magnet and a is its angular acceleration. ∴ α = −μBθ/I --- (1) Since μ, B and I are constants, Eq. (1) shows that angular acceleration is directly proportional to the angular displacement and directed opposite to the angular displacement. Hence the magnet performs angular S.H.M. The period of vibrations of the magnet is given by ∴ T = \(\frac{2π}{\sqrt{α/θ}}=\frac{2π}{\sqrt{\text{angular acceleration per unit angular displacement}}}\) ∴ T = \(\frac{2π}{\sqrt{α/θ}} = 2π\sqrt{\frac{I}{−μB}\)
Damped oscillations : If the amplitude of oscillations of an oscillator is reduced by the application of an external force, the oscillator and its motion are said to be damped.
Periodic oscillations of gradually decreasing amplitude are called damped harmonic oscillations and the oscillator is called a damped harmonic oscillator.
Oscillations of a system in the presence of dissipative frictional forces are damped.
The dissipative damping force removes energy from the system which requires external periodic force to continue.
Figure shows a spring—and-block oscillator attached with a light vane that moves in a fluid with viscosity. When the system is set into oscillation, the amplitude decreases for each oscillation due to the viscous drag on the vane.
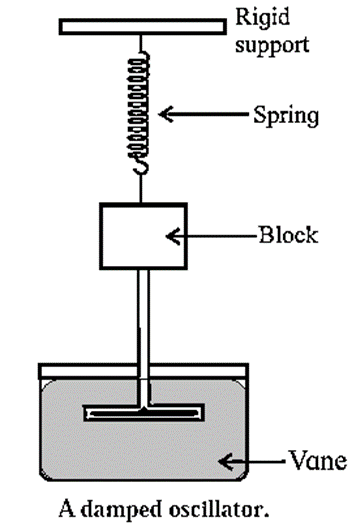
Explanation : The presence of a damping force changes the character of a simple harmonic motion : Consider the oscillations of a body in the presence of a dissipative frictional force such as viscous drag or fluid friction. Such a force is proportional to the velocity of the body and is in a direction opposite to that of the velocity. If the fluid flow past the bod is streamline, then by Stokes’ law, the resistive force is f = −βv = −β(dx/dt) ……(1) where v=dx/dt is the velocity and b is a positive constant of proportionality called the damping constant. The linear restoring force on the oscillator is F = − kx ……..(2) where k is the force constant. If m is the mass of the oscillator and its acceleration is \(\frac{d^2x}{dt^2}\) \(m\frac{d^2x}{dt^2}\) = F + f = −kx −\(β\frac{dx}{dt}\) ∴ \(m\frac{d^2x}{dt^2}+β\frac{dx}{dt}+kx=0\) Or where ω2 =k/m. Equation (3) is the differential equation of the oscillator in presence of a resistive force directly proportional to the velocity. The solution of the above differential equation obtained using standard mathematical technique is x = \(Ae^{-(β/2m)t} cos[\sqrt{ω^2-\frac{β^2}{4m^2}}⋅t+∅]\) ...(4) where constants A and ∅ can be determined in the usual way from the initial conditions. In writing this solution, it is assumed β is less than 2mω, i.e., the resistive term is relatively small. In eq. (4) (1) The harmonic term, \(cos[\sqrt{ω^2-\frac{β^2}{4m^2}}⋅t+∅]\) , shows that the motion is oscillatory with angular frequency ω’ = \(\sqrt{ω^2-\frac{β^2}{4m^2}}\) if b is less than 2mw. The harmonic term can also be written in terms of a sine function with the same w’ (2) A’ = \(Ae^{-(β/2m)t}\) is the amplitude of the oscillation. The exponential factor \(e^{-(β/2m)t}\) steadily decreases the amplitude of the motion, making it approach zero for large t. Hence, the motion is said to be damped oscillation or damped harmonic motion. (3) The total energy, ½ m(ω’A’)2, decays exponentially with time as the amplitude decreases. The energy is dissipated in the form of heat by the damping force. (4) The period of the damped oscillations is T’ = 2π/ω’ = \(\frac{2π}{\sqrt{ω^2-\frac{β^2}{4m^2}}}\) ∴ T’ is greater than 2π/ω Thus, the motion is periodic but not simple harmonic because the amplitude steadily decreases.
\(\frac{d^2x}{dt^2}+\frac{β}{m}\frac{dx}{dt}+ω^2x=0\) …..(3)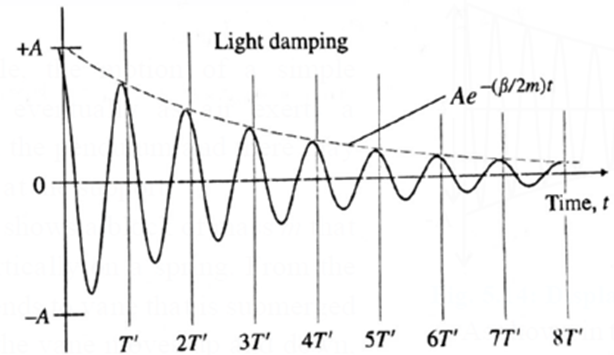
Free vibrations ; A body capable of vibrations is said to perform free vibrations when it is disturbed from its equilibrium position and left to itself.
Example : If the bob of a simple pendulum of length l is displaced and released, it will oscillate only with the frequency
η = \(\frac{1}{2π}{\sqrt{\frac{g}{l}}\) which is called its natural frequency and the oscillations are free oscillations.
- In the absence of dissipative forces such as friction due to surrounding air and internal forces, the total energy and hence the amplitude of vibrations of the body remains constant.
- The frequencies of the free vibrations of a body are called its natural frequencies and depend on the body itself.
- In the absence of a maintaining force, in practice, the total energy and hence the amplitude decreases due to dissipative forces and the vibration is said to be damped.
- The frequency of damped vibrations is less than the natural frequency.
Forced Vibrations : The vibrations of a body in response to an external periodic force are called forced vibrations. The external force supplies the necessary energy to make up for the dissipative losses. The frequency of the forced vibrations is equal to the frequency of the external periodic force. The amplitude of the forced vibrations depends upon the mass of the vibrating body, the amplitude of the external force, the difference between the natural frequency and the frequency of the periodic force, and the extent of damping. Consider the arrangement shown in the Fig. There are four pendula tied to a string. Pendula A and C are of the same length, pendulum B is shorter and pendulum D is longer. Pendulum A is having a solid rubber ball as its bob and will act as the driver pendulum or source pendulum. Other three pendula are having hollow rubber balls as their bobs and will act as the driven pendula. As the pendula A and C are of the same lengths, their natural frequencies are the same. Pendulum B has higher natural frequency as it is shorter and pendulum D is of lower natural frequency than that of A and C.
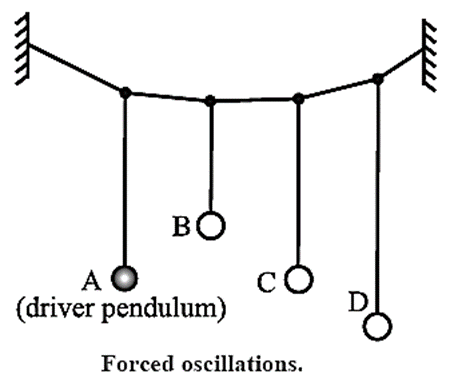
Resonance : If a body is made to vibrate by an external periodic force, whose frequency is equal to the natural frequency (or nearly so) of the body, the body vibrates with maximum amplitude. This phenomenon is called resonance. The corresponding frequency is called the resonant frequency.
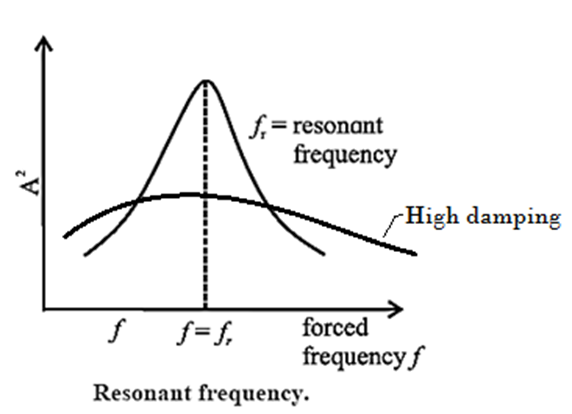
For low damping, the amplitude of vibrations has a sharp maximum at resonance, as shown in Fig. The flatter curve without a pronounced maximum is for high damping.
Distinguish between free vibrations and forced vibrations : Ex. Simple pendulum. 2-The frequency of free vibrations depends on the body and is called its natural frequency. 3-The energy of the body remains constant only in the absence of friction, air resistance, etc. Ex. Musical instrument having a sounding board. 2-The frequency of forced vibrations is equal to that of the external periodic force. 3-The energy of the body is maintained constant by the external periodic force.
Free vibrations
Forced vibrations
1-Free vibrations are produced when a body is disturbed from its equilibrium position and released.
1-Forced vibrations are produced by an external periodic force.
We reply to valid query.