Solutions
Question 1. Choose the correct option.
(i) A conductor has 3 segments; two straight and of length L each and a semicircular with radius R. It carries a current I. What is the magnetic field B at point P?
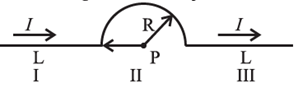
(A) \(\frac{μ_0}{4π}\frac{I}{R}\)
(B) \(\frac{μ_0}{4π}\frac{I}{R^2}\)
(C) \(\frac{μ_0}{4}\frac{I}{R}\)
(d) \(\frac{μ_0I}{4π}\)
(C) \(\frac{μ_0}{4}\frac{I}{R}\)
(ii) Figure a, b show two Amperian loops associated with the conductors carrying current I in the sense shown. The in the cases a and b will be, respectively,
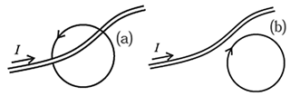
(A) −μ0I, 0
(B) μ0I, 0
(C) 0, μ0I
(D) 0, - μ0I
(A) −μ0I, 0
(iii) A proton enters a perpendicular uniform magnetic field B at origin along the positive x axis with a velocity v as shown in the figure. Then it will follow the following path. [The magnetic field is directed into the paper].
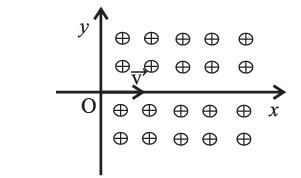
(A) It will continue to move along positive x axis.
(B) It will move along a curved path, bending towards positive x axis.
(C) It will move along a curved path, bending towards negative y axis.
(D) It will move along a sinusoidal path along the positive x axis.
(B) It will move along a curved path, bending towards positive x axis.
(iv) A conducting thick copper rod of length 1 m carries a current of 15 A and is located on the Earth's equator. There the magnetic flux lines of the Earth's magnetic field are horizontal, with the field of 1.3 × 10-4 T, south to north. The magnitude and direction of the force on the rod, when it is oriented so that current flows from west to east, are
(A) 14 × 10−4 N, downward.
(B) 20 × 10−4 N, downward.
(C) 14 × 10−4 N, upward.
(D) 20 × 10−4 N, upward.
(D) 20 × 10−4 N, upward.
(v) A charged particle is in motion having initial velocity when it enter into a region of uniform magnetic field perpendicular to . Because of the magnetic force the kinetic energy of the particle will
(A) remain unchanged.
(B) get reduced.
(C) increase.
(D) be reduced to zero.
(A) remain unchanged.
Question 2. A piece of straight wire has mass 20 g and length 1m. It is to be levitated using a current of 1 A flowing through it and a perpendicular magnetic field B in a horizontal direction. What must be the magnetic of B?
Given : m = 20 g = 2 x 10−2 kg, l = 1 m, I =1 A, g = 9.8 m/s2
To balance the wire, the upward magnetic force must be equal in magnitude to the downward force due to gravity.
∴ Fm= I l B = mg
Therefore, the magnitude of the magnetic field,
B = \(\frac{mg}{Il}=\frac{(2×10^{-2})(9.8)}{1×1}\) = 0.196 T
Question 3. Calculate the value of magnetic field at a distance of 2 cm from a very long straight wire carrying a current of 5 A (Given: μ0 = 4π × 10−7 Wb/Am).
Given : I = 5A, a = 0.02 m, \(\frac{μ_0}{4π}\) = 10−7 T.m/A
The magnetic induction,
B = \(\frac{μ_0I}{2πa}=\frac{μ_0}{4π}\frac{2I}{a}\)
= 10−7 × \(\frac{2(5)}{2×10^{-2}}\) = 5 × 10−5 T
Question 4. An electron is moving with a speed of 3 × 107 m/s in a magnetic field of 6 × 10-4 T perpendicular to its path. What will be the radium of the path? What will be frequency and the energy in keV ?
[Given: mass of electron = 9 ×10-31 kg, charge e = 1.6 × 10-19 C, 1 eV = 1.6 × 10-19 J]
Given : v = 3 x 107 m/s, B = 6 × 10−4 T, me = 9 ×10−31 kg, e = 1.6 × 10−19 C,
1 eV = 1.6 × 10−19 J
The radius of the circular path,
r = \(\frac{m_ev}{|e|B}\) = \(\frac{(9×10^{-31})(3×10^7)}{(1.6×10^{-19})(6×10^{-4}}\) = 0.2812 m
The frequency of revolution,
f = \(\frac{|e|B}{2πm_e}\) = \(\frac{2×3.142(1.6×10^{-19})}{(9×10^{-31})(3×10^7)}\) = 16.97 MHZ
Since the magnetic force does not change the kinetic energy of the charge,
KE = \(\frac{1}{2}m_ev^2\) = \(\frac{1}{2}(9×10^{-31})(3×10^7)\) = \(\frac{81}{2}×10^{-17}\) J
= \(\frac{81}{2×(1.6×10^{-19})}×10^{-17}\)eV
= \(\frac{81}{3.2}×10^3\) = 2.531 keV
Question 5. An alpha particle (the nucleus of helium atom) (with charge +2) is accelerated and moves in a vacuum tube with kinetic energy = 10 MeV. It passes through a uniform magnetic field of 1.88 T, and traces a circular path of radius 24.2 cm. Obtain the mass of the alpha particle.
[1 eV = 1.6 × 10−19 J, charge of electron = 1.6 × 10−19 C]
Given: 1 eV = 1.6 × 10−19 J, E = 10MeV = 107 x 1.6 × 10−19 J = 1.6 × 10−12 J
B = 1.88 T, r = 0.242 m, e = 1.6 × 10−19 C
Charge of an α-particle,
Q = 2e = 2(1.6 × 10−19) = 3.2 × 10−19 C
r = \(\frac{m_αv}{qB}\) and E = \(\frac{1}{2}\)mαv2
∴ r2 = \(\frac{(m_αv)^2}{q^2B^2}\) and 2Emα = (mαv)2
∴ r2 = \(\frac{2Em_α}{q^2B^2}\)
∴ mα = \(\frac{(qBr)^2}{2E}\) = \(\frac{[(3.2×10^{-19})(1.88)(0.242)]^2}{2(1.6×10^{-12})}\)
= (3.2 x 10−26)(1.88 x 0.242)2
= (3.2 x 10−26)(0.455)2
= (3.2 x 10−26)(0.2070) = 6.624 x 10−27 kg
This is the mass of alpha particle
Question 6. Two wires shown in the figure are connected in a series circuit and the same amount of current of 10 A passes through both, but in opposite directions. Separation between the two wires is 8 mm. The length AB is S = 22 cm. Obtain the direction and magnitude of the magnetic field due to current in wire 2 on the section AB of wire 1. Also obtain the magnitude and direction of the force on wire 1. [μ0 = 4π × 10−7 T.m/A]
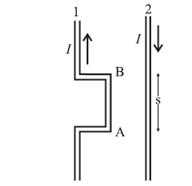
Given : I1 = I2 = 10A, s = 8 mm = 8 x 10−3m, l = 0.22 m
By right hand grip rule, the direction of the magnetic field due to the current in wire 2 at AB is into the page and its magnitude is
B2 = \(\frac{μ_0}{4π}\frac{2I}{s}\) = 10-7 x \(\frac{2×10}{8×10^{-3}}\) T
The current in segment AB is upwards. Then, by Fleming's left hand rule, the force on it due to is to the left of the diagram, i.e., away from wire 1, or repulsive. The magnitude of the force is
Fon 1 by 2 = I1lB2= (10)(0.22) × \(\frac 14\) × 10−3
= 5.5 × 10−4 N
Question 7. A very long straight wire carries a current 5.2 A. What is the magnitude of the magnetic field at a distance 3.1 cm from the wire? [μ0 = 4 π × 10−7 T.m/A]
Given : I = 5.2 A, a = 0.031 m, μ0 /4π = 10−7 T.m/A
The magnetic induction,
B = \(\frac{μ_0I}{2πa}=\frac{μ_0}{4π}\frac{2I}{a}\)
= 10−7 × \(\frac{2(5.2)}{3.1×10^{-2}}\)
= 3.35 × 10−5 T
Question 8. Current of equal magnitude flows through two long parallel wires having separation of 1.35 cm. If the force per unit length on each of the wires in 4.76 × 10−2 N, what must be I ? [u0/4 π = 10−7T.m/A]
Given : I1 = I2 = I, s = 1.35 x 10−2 m, F/l = 4.76 × 10−2 N
F = \((\frac{μ_0}{4π})\frac{2I_1I_2l}{s}\) = \((\frac{μ_0}{4π})\frac{2I^2l}{s}\)
∴ I2 = \(\frac{F}{l}\frac{s}{2(μ_0/4π)}\) = (4.76 × 10−2)\(\frac{1.35×10^{-2}}{2×10^{-7}}\) = 3.213 x 103
∴ I = \(\sqrt{32.13×10^2}\) = 56.68 A
Question 9. Magnetic field at a distance 2.4 cm from a long straight wire is 16 μT. What must be current through the wire?
Given : a = 0.024 m,B = 1.6 x 10−5 T, μ0 /4π = 10−7 T.m/A
B = \(\frac{μ_0I}{2πa}=\frac{μ_0}{4π}\frac{2I}{a}\)
The current through the wire,
I = \(\frac{1}{μ_0/4π}\frac{aB}{2}\)
= \(\frac{1}{10^{-7}}\frac{(2.4×10^{-2})(1.6×10^{-5})}{2}\) = 1.92 A
Question 10. The magnetic field at the centre of a circular current carrying loop of radius 12.3 cm is 6.4 × 10−6 T. What will be the magnetic moment of the loop?
Given : R = 12.3 cm = 12.3 × 10−2 m, B = 6.4 x 10−6 T, μ0 = 4π x 10−7 T.m/A
B = \(\frac{μ_0I}{2R}\) = \(\frac{μ_0I}{2R}\frac{2πR^2}{2πR^2}\) = \(\frac{μ_0I}{4π}\frac{2I(A)}{R^3}\) …(∵ A = πR2)
= \(\frac{μ_0I}{4π}\frac{2μ}{R^3}\)
where μ = IA is the magnetic dipole moment of the coil.
∴ μ = \(\frac{BR^3}{2(μ_0/4π}\) = \(\frac{(6.4×10^{-6}(0.123)^3}{2×10^{-7}}\) = 5.955 x 10−2 J/T (or A.m2)
Question 11. A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field (a) at the centre of the loop and (b) at a distance of 9.7 cm from the centre of the loop but on the axis.
Given: R = z = 9.7cm = 9.7 x 10−2 m, I = 2.3 A, N = 1
(a) At the centre of the coil :
The magnitude of the magnetic induction,
B = \(\frac{μ_0NI}{2R}\)
= \(\frac{(4π×10^{-7})(1)(2.3)}{2(9.7×10^{-2})}\)
= \(\frac{2×3.142×2.3}{9.7}×10^{-5}\)
= 1.49 x 10−5 T
(b) On the axis, at a distance z = 02 m from the coil :
B = \(\frac{μ_0}{4π}\frac{2πIR^2}{(R^2+z^2)^{3/2}}\)
(R2 + z2)3/2 = (2R2)3/2 = 2\(\sqrt{2}\)R3 (∵ R = z)
∴ B = \(\frac{μ_0}{4π}\frac{2πIR^2}{2\sqrt{2}R^3}\)
= \(\frac{μ_0}{4π}\frac{πI}{\sqrt{2}R}\)
= (10−7)\(\frac{3.142×2.3}{1.414×9.7×10^{-2}}\)
= 5.267 x 10−6 T = 5.267 μT
Question 12. A circular coil of wire is made up of 100 turns, each of radius 8.0 cm. If a current of 0.40 A passes through it, what be the magnetic field at the centre of the coil?
Given : N = 100, R = 8 x 10−2 m, I = 0.4 A, μ0 = 4 π x 10−7 T.m/A
B = \(\frac{μ_0NI}{2R}\)
= \(\frac{(4π×10^{-7})(100)(0.4)}{2(8×10^{-2})}\)
= 3.142 x 10−4 T
Question 13. For proton acceleration, a cyclotron is used in which a magnetic field of 1.4 Wb/m2 is applied. Find the time period for reversing the electric field between the two Ds. (Proton mass = 1.67 × 10−27 kg, e = 1.60 × 10−19 C, eV = 1.6 × 10−19 J)
Given : B= 1.4 Wb/m2, m = 1.67 x 10−27 kg, q = 1.6 × 10−19 C
T = \(\frac{2πm}{qB}\)
t = \(\frac{T}{2}\) = \(\frac{πm}{qB}=\frac{(3.142)(1.67×10^{-27})}{(1.6×10^{-19})(1.4)}\)
= 2.342 × 10−8 s
This is the required time interval.
Question 14. A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
Given : N = 50, C = 1.5 x 10−9 N-m/degree, A = lb = 5 cm x 3 cm = 15 cm2 = 15 x 10−4 m2, B = 0.05 Wb/m2, θ = 30°
NIAB = Cθ
∴ The current through the coil I = \(\frac{Cθ}{NAB}\)
= \(\frac{(1.5×10^{-9})×30}{50×15×10^{-4}×0.05}\)
= \(\frac{3×10^{-5}}{5×0.5}\)
= 1.2 x 10−5 A
Question 15. A solenoid of length π m and 5 cm in diameter has winding of 1000 turns and carries a current of 5 A. Calculate the magnetic field at its centre along the axis.
Given : L = 3.142 m, N = 1000, I = 5A, μ0 = 4 π x 10−7 T.m/A
The magnetic induction,
B = μ0 nI = μ0\((\frac{N}{L})I\)
= (4 π x 10-7)\(\frac{1000}{3.142}\)(5)
= 2 x 10−3 T
Question 16. A toroid of narrow radius of 10 cm has 1000 turns of wire. For a magnetic field of 5 × 10−2 T along its axis, how much current is required to be passed through the wire?
Given : Central radius, r = 10 cm = 0.1 m, N = 1000, B = 5 x 10−2 T, μ0 = 4 π x 10−7 T.m/A
The magnetic induction,
B = \(\frac{μ_0NI}{2πR}\) = \(\frac{μ_0}{4π}\frac{2NI}{r}\)
∴ 5 x 10-2 = 10−7 x \(\frac{2(1000)I}{0.1}\)
∴ l = 50/2 = 25 A
Question 17. In a cyclotron protons are to be accelerated. Radius of its D is 60 cm. and its oscillator frequency is 10 MHz. What will be the kinetic energy of the proton thus accelerated? (Proton mass = 1.67 × 10-27 kg, e = 1.60 × 10−19 C, eV = 1.6 × 10−19 J)
Given : R = 0.6 m, f = 107 Hz, mp = 1.67 × 10−27 kg, e = 1.6 x 10−19 C,
1 eV = 1.6 x 10−19 J
f = \(\frac{qB}{2πm_p}\) and KE = \(\frac{q^2B^2R^2}{2m_p}\)
∴ f2 = \(\frac{q^2B^2}{4π^2m_p^2}\) ∴ \(\frac{q^2B^2}{2m_p}\) = 2π2fmp
∴ KE = 2π2fmpR2
= 2 x 9.872 x (107)(1.67 × 10−27)(0.6)2
= 11.87 x 10-13 J = \(\frac{11.87×10^{-13}}{1.6×10^{-19}}\)
= 7.419 x 106 ev
= 7.419 Mev
Question 18. A wire loop of the form shown in the figure carries a current I. Obtain the magnitude and direction of the magnetic field at P.
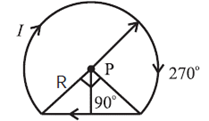
The wire loop is in the form of a circular arc AB of radius R and a straight conductor BCA. The arc AB subtends an angle of ø = 270° = \(\frac{3π}{2}\) rad at the centre of the loop P. Since PA = PB = R and C is the midpoint of AB, AB = \(\sqrt{2}\)R and AC = CB = \(\frac{\sqrt{2}R}{2}\) = \(\frac{R}{\sqrt{2}}\)
Therefore, a = PC = \(\frac{R}{\sqrt{2}}\)
The magnetic inductions at P due to the arc AB and the straight conductor BCA are respectively,
B1 = \(\frac{μ_0}{4π}\frac{Iø}{R}\) and B2 = \(\frac{μ_0}{4π}\frac{2I}{a}\)
Therefore, the net magnetic induction at P is
Bnet = B1 + B2 = \(\frac{μ_0}{4π}I[\frac{ø}{R}+\frac{2}{r/\sqrt{2}}]\)
= \(\frac{μ_0}{4π}\frac{I}{R}[ø+2\sqrt{2}]\)
= \(\frac{μ_0}{4π}\frac{I}{R}[\frac{3π}{2}+2\sqrt{2}]\)
This is the required expression.
Question 19. Two long parallel wires going into the plane of the paper are separated by a distance R, and carry a current I each in the same direction. Show that the magnitude of the magnetic field at a point P equidistant from the wires and subtending angle θ from the plane containing the wires, is B = sin 2θ. What is the direction of the magnetic field?
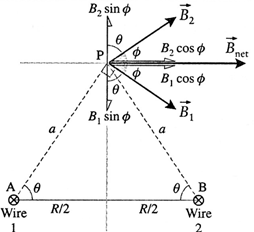
In above Fig. and are the magnetic fields in the plane of the page due to the currents in wires 1 and 2, respectively. Their directions are given by the right hand grip rule : is perpendicular to AP and makes an angle ø with the horizontal. is perpendicular to BP and also makes an angle ø with the horizontal.
AP = BP = a = \(\frac{R/2}{cos\,θ}\)
And B1 = B2 = \(\frac{μ_0}{4π}\frac{2I}{a}\) = \(\frac{μ_0}{4π}\frac{2I(2cos\,θ)}{R}\) = \(\frac{μ_0}{π}\frac{I}{R}cos\,θ\)
Since the vertical components cancel out, the magnitude of the net magnetic induction at P is
Bnet = 2B1 cos ø = 2B1 cos (90- θ) = 2B1 sin θ
= 2\((\frac{μ_0}{π}\frac{I}{R}cos\,θ)\) sin θ
= \(\frac{μ_0}{π}\frac{I}{R}sin\,2θ\)
as required \(\vec{B}_{net}\) is in the plane parallel to that of the wires and to the right as shown in the figure.
Question 20. Figure shows a cylindrical wire of diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radial distance r from the axis according to the relation J = Jo r/a. Obtain the magnetic field B inside the wire at a distance r from its centre.
Consider an annular differential element of radius r and width dr. The current through the area dA of this element is
dI = JdA = \((J_0\frac{r}{a})\)2πrdr = \(\frac{2πJ_0r^2dr}{a}\) …..(1)
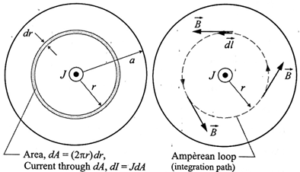
To apply the Ampere's circuital law to the circular path of integration, we note that the wire has perfect cylindrical symmetry with all the charges moving parallel to the wire. So, the magnetic field must be tangent to circles that are concentric with the wire. The enclosed current is the current within radius r. Thus,
∴ \(\oint Bdl=μ_0I_{encl}\)
= \(\oint Bdl=μ_0\int_0^r{dl}=μ_0\int_0^r \frac{2πJ_0}{a}r^2dr\) …..(2)
∴ B (2πr) = \(\frac{μ_02πJ_0}{a}(\frac{r^3}{3})\)
∴ B = \(\frac{μ_0J_0}{3a}r^2\) …..(3)
This is the required equation.
Question 21. In the above problem, what will be the magnetic field B inside the wire at a distance r from its centre, if the current density J is uniform across the cross section of the wire?
In above problem figure shows the cross section of a long straight wire of radius a that carries a current I out of the page. Because the current is uniformly distributed over the cross section of the wire, the magnetic field \(\vec{B}\) due to the current must be cylindrically symmetrical.
Thus, along the Amperian loop of radius r (r <a), symmetry suggests that \(\vec{B}\) is tangent to the loop, as shown in the figure.
\(\oint \vec{B}.\vec{dl} B\oint dl\) = B (2πr) …..(1)
Because the current is uniformly distributed, the current Iencl enclosed by the loop is proportional to the area encircled by the loop; that is,
Iencl =Jπr2
By right-hand rule, the sign of Iencl is positive. Then, by Ampere's law,
B (2πr) = μ0Iencl = μ0Jπr2 …..(2)
∴ B = \(\frac{μ_0J_0}{2}r\) …..(3)
OR
Iencl = \(I\frac{πr^2}{πa^2}\)
By right-hand rule, the sign of Iencl is positive. Then, by Ampere's law,
\(\oint Bdl=μ_0I_{encl}\)
∴ B (2πr) = μ0Iencl = \(μ_0I\frac{r^2}{a^2}\) …..(4)
∴ B = \((\frac{μ_0I}{2πa^2})r\) …..(5)
We reply to valid query.