Notes
|
Topics to be learn :
|
Probability : Introduction
(i) If each student in the class toss a coin once :
| Possibilities | (H) | (T) |
| Number of students | x | y |
Each student will either get a head (H) or a tail (T).
How many students get a head and how many students get a tail can be decided.
(ii) If each student to toss the same coin twice, then the possibilities are :
| Possibilities | (HH) | (HT) | (TT) | (TH) |
| Number of students | p | q | r | s |
In this activity each student will get any one of the above four possibilities.
(iii) If we throw a die once, then the different possibilities of getting dots on the upper face are :
Each of these is a possible result of throwing a die When a die is thrown, there are six possibilities At a time, only one of the six is possible.
Random experiment and its outcome :
An experiment in which all the possible results are known in advance, but none of them can be predicted with certainty is called a random experiment.
The following are some examples of random experiments :
- (i) Tossing a coin
- (ii) Throwing a die
- (iii) Picking a card from a set of cards bearing numbers from 1 to 50,
- (iv) Drawing a card from a well-shuffled pack of 52 playing cards, etc.
Outcome :
Result of a random experiment is known as an ‘Outcome’.
- (i) In a random experiment of tossing a coin - there are only two outcomes. Head (H) or Tail (T)
- (ii) In a random experiment of throwing a die, there are 6 outcomes, according to the number of dots on the six faces of the die. 1 or 2 or 3 or 4 or 5 or 6.
- (iii) In a random experiment of picking a card bearing numbers from 1 to 50, there are 50 outcomes.
- There are four suits in a pack of playing cards. Spades, hearts, diamonds and clubs. Each suit has 13 cards. Spade and Club are black cards. Heart and Diamond are red cards. King, Queen and Jack are called face cards. The card bearing number 1 is called Ace card. Ace card is not a face card. So we have fifty-two possible outcomes.
Equally Likely Outcomes :
A given number of outcomes are said to be equally likely, if none of them is expected to occur in preference to the others.
Example :
- When we toss a coin, the head or tail is the equally likely outcome.
- If a die is thrown, any of the numbers from 1, 2, 3, 4, 5, 6 may appear on the upper face. It means that each number is equally likely to occur.
Question : In which of the following experiments is the possibility of expected outcome more?
(i) Getting 1 on the upper face when a die is thrown.
(ii) Getting head by tossing a coin.
(i) There are 6 numbers on a die, there are 6 possibilities of getting any one number from 1 to 6 on the upper face. i.e. \(\frac{1}{6}\) is the possibility.
(ii) There are two possibilities (H or T) on tossing a coin. i.e. (\frac{1}{2}\) is possibility.
So, the expected outcome is more in experiment (ii).
Sample space and event :
Sample space : The set of all possible outcomes of a random experiment is called the sample space. A sample space is denoted by S or Ω (omega).
- The number of elements in the set S (i.e. number of sample points) is denoted by n(S). The sample space is called a finite sample space, if n(S) is finite.
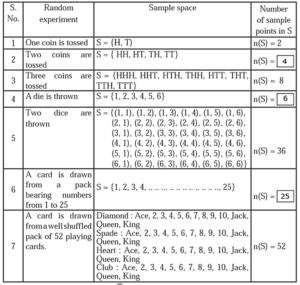
Remember :
- Tossing a coin twice gives the same sample space as tossing two coins simultaneously. The same holds true with three coins.
- Rolling a die twice produces the same sample space as rolling two dice together.
Event : The outcomes satisfying a particular condition are called favourable outcomes. A set of favourable outcomes of a given sample space is an event.
- Event is a subset of the sample space.
- Events are generally denoted by capital letters A,B, C, D, etc.
Examples :
(i) If two coins are tossed and A is the event of getting at least one tail, then the favourable outcomes are as : A = {TT, TH, HT}
The number of elements in the event A is denoted by n(A). Here n(A) = 3.
(ii) Two coins are tossed simultaneously. Write the sample space (S) and number of sample points n(S). Also write the following events in the set form and write
the number of sample points in each event.
(i) Condition for event A : to get at least one tail.
(ii) Condition for event B : to get only one head.
(iii) Condition for event C : to get at most one tail.
(iv) Condition for event D : to get no head.
Solution :
| If two coins are tossed simultaneously, | S = {HH, HT, TH, TT} n(S) = 4 |
| (i) Condition for event A : at least one head. | A = {HH, HT, TH} n(A) = 3 |
| (ii) Condition for event B : only one head. | B = { HT, TH} n(B) = 2 |
| (iii) Condition for event C : at most one tail. | C = {HH, HT, TH} n(C) = 3 |
| (iv) Condition for event D : No head. | D = {TT} n(D) = 1 |
Probability of an event :
The probability of an event A in a finite sample space S, is written as P(A) and is defined as
P(A) = \(\frac{\text{Number of sample points in event A}}{\text{Number of sample points in sample spaces}}=\frac{n(A)}{n(S)}\)
When possibility of an expected event is expressed in number, it is called ‘Probability’. It is expressed as a fraction or percentage
Example :
(i) A bag contains 4 balls of the same size. Three of them are white and the fourth is black. You are supposed to pick one ball at random without seeing it. Find out possibility of getting a white ball and a black ball.
Answer :
Getting a white ball is event A.
As there are three white balls n(A) = 3,
As the number of balls is 4, n(S) = 4
∴ probability of getting a white ball is, P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{4}\)
Similarly, if getting black ball is event B, then n(B) = 1
∴ probability of getting a black ball is, P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{4}\)
Remember :
The Probability is expressed as a fraction or a percentage.
The probability of any event is from 0 to 1 or 0% to 100%.
- If E is any event, 0 ≤ P(E) ≤ 1 or 0 % ≤ P(E) ≤ 100 %. e.g. probability ¼ is written as 25 %.
We reply to valid query.