Electric Current Through Conductors
Maharashtra Board-Class-11-Science-Physics-Chapter-11
Solution
Question 1. Choose correct alternative
(i) You are given four bulbs of 25 W, 40 W, 60 W and 100 W of power, all operating at 230 V. Which of them has the lowest resistance?
(A) 25 W
(B) 40 W
(C) 60 W
(D) 100 W
(D) 100 W
Explanation :
P = \(\frac{V^2}{R}\)
Since all the bulbs are operating at the same volt.
∴ P ∝ 1/R
∴ The bulb with the highest power will have the lowest resistance. i.e., 100 W bulb
(ii) Which of the following is an ohmic conductor?
(A) transistor
(B)vacuum tube
(C) electrolyte
(D) nichrome wire
(D) nichrome wire
(iii) A rheostat is used
(A) to bring on a known change of resistance in the circuit to alter the current
(B) to continuously change the resistance in any arbitrary manner and there by alter the current
(C) to make and break the circuit at any instant
(D) neither to alter the resistance nor the current
(B) to continuously change the resistance in any arbitrary manner and there by alter the current
(iv) The wire of length L and resistance R is stretched so that its radius of cross-section is halved. What is its new resistance?
(A) 5R
(B) 8R
(C)4R
(D) 16R
(D) 16R (assuming that the volume of the wire does not change when it is stretched)
(v) Masses of three pieces of wires made of the same metal are in the ratio 1:3:5 and their lengths are in the ratio 5:3:1. The ratios of their resistances are
(A) 1:3:5
(B) 5:3:1
(C) 1:15:125
(D) 125:15:1
(D) 125:15:1
Explanation :
R = ρ\(\frac{l}{A}\) = ρ\(\frac{l×l}{A×l}\) = ρ\(\frac{l^2}{V}\)
Since V = m/d
R = ρ\(\frac{l^2}{m/d}\) , ∴ R ∝ \(\frac{l^2}{m}\)
∴ R1 : R2 : R3 = \(\frac{l_1^2}{m_1}\) : \(\frac{l_2^2}{m_2}\) : \(\frac{l_3^2}{m_3}\)
∴ R1 : R2 : R3 = \(\frac{5^2}{1}\) : \(\frac{3^2}{3}\) : \(\frac{1^2}{5}\) = \(\frac{25}{1}\) : \(\frac{9}{3}\) : \(\frac{1}{5}\)
Then R1 : R2 : R3 = 125 : 15 : 1
(vi) The internal resistance of a cell of emf 2V is 0.1Ω it is connected to a resistance of 0.9Ω. The voltage across the cell will be
(A) 0.5 V
(B) 1.8 V
(C) 1.95 V
(D) 3V
(B) 1.8 V
(vii) 100 cells each of emf 5V and internal resistance 1Ω are to be arranged so as to produce maximum current in a 25Ω resistance. Each row contains equal number of cells. The number of rows should be
(A) 2
(B) 4
(C) 5
(D) 100
(A) 2
Explanation :
let, m = Number of rows, n = Number of cells in a row
∴ m x n = 100 ..... (i)
Resistance is series = nr
Resistance in parallel = m/nr
For maximum current, R = nr/m
25 = (n x 1)/m = n/m ….(ii)
From (i) and (ii)
m x 25m = 100
∴ m2 = 100/25 = 4
∴ m = 2
(viii) Five dry cells each of voltage 1.5 V are connected as shown in diagram
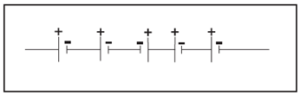
What is the overall voltage with this arrangement?
(A) 0V
(B) 4.5V
(C) 6.0V
(D) 7.5V
(B) 4.5V
Explanation :
(4 x 1.5) – (1.5) = 6 - 1.5 = 4.5 V
Question 2. Give reasons / short answers
(i) In given circuit diagram two resistors are connected to a 5V supply.
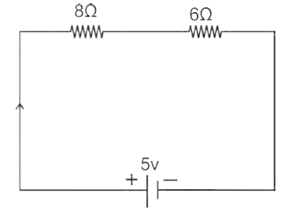
[a] Calculate potential difference across the 8 Ω resistor.
[b] A third resistor is now connected in parallel with 6 Ω resistor. Will the potential difference across the 8 Ω resistor the larger, smaller or the same as before? Explain the reason for your answer.
Given : R1 = 8 Ω, R2 = 6 Ω, V = 5 V, series combination
(a) The current in the circuit, I = \(\frac{V}{R}=\frac{V}{R_1+R_2}=\frac{5}{8+6}\) = \(\frac{5}{14}\)A
Hence, the potential difference across 8 Ω resistor,
V1 = R1I = 8 x \(\frac{5}{14}\) = \(\frac{20}{7}\) V = 2.857 V
(b) Reason: As per the question, the new circuit diagram will be
When a third resistor, say R, is connected in parallel with 6 Ω resistor, the resistance of the parallel combination of R and 6 Ω will be less than 6 Ω. Therefore, the total resistance in the circuit will be less than 14 Ω. Hence, the current in the circuit will be more than \(\frac{5}{14}\)A.
Hence, the potential difference across 8 Ω resistor will be larger than earlier value ( \(\frac{20}{7}\)V).
(ii) Prove that the current density of a metallic conductor is directly proportional to the drift speed of electrons.
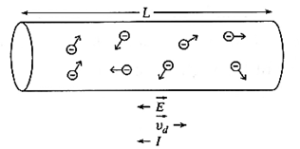
Let A be the area of cross section of a conducting wire across which an electric field \(\vec{E}\) is applied, resulting in a current I.
Consider a section of length L of the wire. See above Fig for reference.
The volume of this part of the wire is AL. If n is the number of free electrons per unit volume of the material of the wire, the number of free electrons in volume AL is nAL. The charge carried by the free electrons in this part is q = nALe, where e denotes the electron charge.
If vd is the drift speed of the electrons, the time taken by the electrons to cover the distance L is t = L/vd (‘.’ vd = L/t).
The charge q is transported across a cross section of the wire in time t. Hence, the corresponding current is
I = q/t = \(\frac{nALe}{L/v_d}\) = nAvde
Hence, the current density, i.e., the current per unit cross sectional area is
J = I/A = \(\frac{nAv_de}{A}\) = (ne)vd.
For a given material, ne = constant. ∴ J ∝ vd
The direction of \(\vec{J}\) is the direction of the current. It is opposite to that of drift velocity \(\vec{v_d}\).
Question 3. Answer the following questions.
(i) Distinguish between Ohmic and nonohmic substances; explain with the help of example.
(a) Ohmic conductor: A conductor or a device which obeys Ohm’s law is called an ohmic conductor.
A graph of current (I) versus the potential difference (V) across an ohmic conductor is a straight line through the origin, provided its physical state remains the same, as shown in the following figure :

Hence, the ratio V/I = R, which is the reciprocal of the slope of the straight line, is the same for all values of V. In other words, the resistance of the conductor is independent of the magnitude and polarity of V.
The resistance of a conductor changes with temperature. Hence, the graph is not a straight line when the temperature of the conductor increases due to either prolonged passage of current or passage of a large current.
- Examples : Metals and metallic alloys, e.g., silver, copper, aluminium, iron, manganin, Nichrome, constantan, etc.
(b) Non-ohmic conductor : A conductor or a device which does not obey Ohm’s law is called a non-ohmic conductor.
A graph of current versus potential difference across a non-ohmic conductor is a curve as shown in Fig. for a pn—junction diode (semiconductor diode). That is, the resistance of such a conductor changes with the applied potential difference.
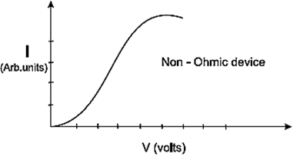
If for a certain potential difference V the current through the conductor is I, then its resistance at that V is given by
R = \(\lim\limits_{ΔI\to 0} \frac{ΔV}{ΔI}=\frac{dV}{dI}\)
where ΔV is the potential difference between the two values of potential V\(-\frac{ΔV}{2}\), V +\(-\frac{ΔV}{2}\) , and ΔI is the corresponding change in the current.
- Examples : Liquid electrolytes, vacuum tubes, junction diodes, thermistors etc.
(ii) DC current flows in a metal piece of nonuniform cross-section. Which of these quantities remains constant along the conductor: current, current density or drift speed?
Current remains constant along the conductor.
Question 4. Solve the following problems.
(i) What is the resistance of one of the rails of a railway track 20 km long at 20° C? The cross section area of rail is 25 cm2 and the rail is made of steel having resistivity at 20° C as 6 × 10-8 Ω m.
Given : l = 20 km = 2 × 104 m, T = 20 °C, A = 25 cm2 = 2.5 × 10-3 m2,
ρ at 20°C = 6 x 10-8 Ω.m.
The resistance of the rail,
R = ρ\(\frac{l}{A}\) = 6 x 10-8\(\frac{2×10^4}{2.5×10^{-3}}\)= 6 × 0.8 × 10-1 = 0.48 Ω
(ii) A battery after a long use has an emf 24 V and an internal resistance 380 Ω. Calculate the maximum current drawn from the battery? Can this battery drive starting motor of car?
Given : ε = 24 V, r = 380 Ω
(i) The maximum current that can be drawn from the battery = \(\frac{ε}{r}=\frac{24}{380}\) = 0.0632 A
(ii) As the value of the current is very small compared to the required current to run a starting motor of a car, this battery cannot be used to drive the motor.
(iii) A battery of emf 12 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A,
[a] Calculate resistance of resistor.
[b] Calculate terminal voltage of the battery when the circuit is closed.
Given : ε = 12 V, r = 3 Ω, I = 0.5 A
[a] I = \(\frac{ε}{R+r}\) ∴ R = \(\frac{ε-Ir}{I}\) = \(\frac{12-(0.5)(3)}{0.5}\) = 24 – 3 = 21 Ω
This is the resistance of the resistor.
(b) The terminal voltage when the circuit is closed,
V = IR = (0.5) (21) = 10.5 V
(iv) The magnitude of current density in a copper wire is 500 A/cm2. If the number of free electrons per cm3 of copper is 8.47 × 1022 calculate the drift velocity of the electrons through the copper wire (charge on an e = 1.6 × 10-19 C)
Given : J = 500 A/cm2 = (500 A)/(10-4 m2) = 5 x 106 A/m2,
N = 8.47 x 1022 free electrons/cm3 = 8.47 x 1028 free electrons/m3, e = 1.6 x 10-19 C
vd = \(\frac{J}{ne}\) = \(\frac{5×10^6}{(8.47×10^{28})(1.6×10^{-19})}\)
= \(\frac{50}{8.47×1.6}\) × 10-4 = 3.689 × 10-4 m/s
The drift velocity of the electrons in the copper wire is 3.689 × 10-4 m/s
(v) Three resistors 10 Ω, 20 Ω and 30 Ω are connected in series combination.
[i] Find equivalent resistance of series combination.
[ii] When this series combination is connected to 12V supply, by neglecting the value of internal resistance, obtain potential difference across each resistor.
Given : R1 = 10 Ω, R2 = 20 Ω, R3 = 30 Ω, V = 12 V
(i) R = R1 + R2 + R3 = 10 +20 + 30 = 60 Ω
(ii) Potential difference,
V1 = R1I = R1\((\frac{V}{R})\) = 10\((\frac{12}{60})\) = 10\((\frac{1}{5})\) = 2 V
V2 = R2I = R2\((\frac{V}{R})\) = 20\((\frac{1}{5})\) = 4 V
V3 = R3I = R3\((\frac{V}{R})\) = 30\((\frac{1}{5})\) = 6 V
(vi) Two resistors 1k Ω and 2k Ω are connected in parallel combination.
[i] Find equivalent resistance of parallel combination
[ii] When this parallel combination is connected to 9 V supply, by neglecting internal resistance calculate current through each resistor.
Given : R1 = 1 k Ω = 103 Ω, R2 = 2 k Ω = 2 x 103 Ω, V = 9 V
(i) \(\frac{1}{R_P} = \frac{1}{R_1}+\frac{1}{R_2}\) = \(\frac{1}{1}+\frac{1}{2}\) = \(\frac{3}{2}\)
∴ RP = \(\frac{2}{3}\) = 0.6666 k Ω
(ii) Current I1 = \(\frac{V}{R_1}\) = \(\frac{9}{1×10^3}\) = 9 x 10-3 A
I2 = \(\frac{V}{R_2}\) = \(\frac{9}{2×10^3}\) = 4.5 x 10-3 A
(vii) A silver wire has a resistance of 4.2 Ω at 27° C and resistance 5.4 Ω at 100° C. Determine the temperature coefficient of resistance.
Given : R1 = 4.2 Ω, T1 = 27 0C, R2 = 5.4 Ω, T2 = 100 °C,
R = R0 [1 + ∝ (T - T0)] = R0 (1 + ∝T) for T0 = 0 0C
∴ R1 = R0 (1 + ∝T1) and R2 = R0 (1 + ∝T2)
∴ \(\frac{R_2}{R_1}\) = \(\frac{1+∝T_2}{1+∝T_1}\)
∴ R2 + R2∝T1 = R1 + R1∝T2
∴ R2 - R1 = ∝(R1T2 - R2T1)
∴ The temperature coefficient of resistance,
∝ = \(\frac{R_2-R_1}{R_1T_2-R_2T_1}\) = \(\frac{5.4-4.2}{4.2×100-5.4×27}\)
= \(\frac{1.2}{420-145.8}\) = \(\frac{1.2}{274.2}\) = 4.376 × 10-3/0C
(viii) A 6m long wire has diameter 0.5 mm. Its resistance is 50 Ω. Find the resistivity and conductivity.
Given : R = 50 Ω, l = 6 m, d = 0.5 mm, r = d/2 = 0.25 mm = 2.5 x 10-4
R = ρ\(\frac{l}{A}\) = ρ\(\frac{l}{πr^2}\)
∴ The resistivity, ρ = \(\frac{Rπr^2}{l}\) = \(\frac{(50)(3.142)(2.5×10^{-4})^2}{6}\) = 1.636 x 10-6 Ω.m
The conductivity, σ = \(\frac{1}{ρ}=\frac{1}{1.636×10^{-6}}\) = 6.112 x 105 Ω.m
(ix) Find the value of resistances for the following colour code.
(1) Blue Green Red Gold
(2) Brown Black Red Silver
(3) Red Red Orange Gold
(4) Orange White Red Gold
(5) Yellow Violet Brown Silver
(1)
| Color | Blue | Green | Red | Gold |
| Value | 6 | 5 | 102 | ±5% |
∴ R = 65 x 102 Ω ±5% = 6.5 x 103 Ω ±5% = 6.5 k Ω ±5% = (6500 ± 325) Ω
(2)
| Color | Brown | Black | Red | Silver |
| Value | 1 | 0 | 102 | ±10% |
∴ R = 10 x 102 Ω ±10% = 1.0 x 103 Ω ±10% = 1.0 k Ω ±10% = (1000 ± 100) Ω
(3)
| Color | Red | Red | Orange | Gold |
| Value | 2 | 2 | 103 | ±5% |
∴ R = 22 x 103 Ω ±5% = 22 k Ω ±5% = (22000 ± 1100) Ω
(4)
| Color | Orange | White | Red | Gold |
| Value | 3 | 9 | 102 | ±5% |
∴ R = 39 x 102 Ω ±5% = 3.9 x 103 Ω ±5% = 3.9 k Ω ±5% = (3900 ± 195) Ω
(5)
| Color | Yellow | Violet | Brown | Silver |
| Value | 4 | 7 | 101 | ±10% |
∴ R = 47 x 10 Ω ±10% = 470 Ω ±10% = (470 ± 47) Ω
(x) Find the colour code for the following value of resistor having tolerance ± 10% (a) 330Ω (b) 100Ω (c) 47kΩ (d) 160Ω (e) 1kΩ
(a) 330 Ω → Orange, Orange, Brown, Silver
(b) 100 Ω → Brown, Black, Brown, Silver
(c) 47 Ω → Yellow, Violet, Orange, Silver
(d) 160 Ω → Brown, Blue, Brown, Silver
(e) 1 k Ω → Brown, Black, Red, Silver.
(xi) A current 4A flows through an automobile headlight. How many electrons flow through the headlight in a time 2hrs.
Given : I = 4 A, t = 2 h = 2 x 3600 s = 7200 s, |e|= 1.6 ×10-19 C
I = \(\frac{q}{t}\) = \(\frac{n|e|}{t}\)
∴ n = \(\frac{It}{|e|}\) = \(\frac{4×7200}{1.6×10^{-19}}\) = \(\frac{72}{4}\) x 1022 = 1.8 x 1023
1.8 x 1023 number of electrons flow through the headlight in 2hrs.
(xii) The heating element connected to 230V draws a current of 5A. Determine the amount of heat dissipated in 1 hour.
Given : V = 230 V, I = 5 A, t = 1h = 3600 s, J = 4.2 J/cal
The amount of heat dissipated,
H = \(\frac{VIt}{J}\) = \(\frac{(230)(5)(3600)}{4.2}\) = 9.857 x 105 cal = 985.7 kcal
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 10: Electrostatics – Online Solutions
Next Chapter : Chapter 12: Magnetism – Online Solutions
We reply to valid query.