Notes-Part-2
Topics to be Learn : Part-2
|
Boiling point elevation : The boiling point of liquid is the temperature at which its vapour pressure equals the applied pressure. For liquids in open containers the applied pressure is atmospheric pressure.
Effect of temperature on the vapour pressure of a liquid :
The vapour pressure of a liquid is the pressure of the vapour in equilibrium with the liquid at a given temperature.
The evaporation of a liquid requires thermal energy. Hence, as temperature rises, the vapour pressure rises until it becomes equal to the external pressure, generally the atmospheric pressure, 101.3 kNm-2 (1 atm). This temperature is called the normal boiling point of the liquid.
Elevation in the boiling point of a solution :
The elevation in the boiling point of a solution is defined as the difference between the boiling points of the solution and the pure solvents at a given pressure, e.g. If To and T are the boiling points of a pure solvent and a solution, then the elevation in boiling point, ΔT = T— T0. It is a colligative property.
Boiling point elevation as a consequence of vapour pressure lowering :
- The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the external pressure, generally 1 atm (101.3 x 103 Nm-2). When a liquid is heated, its vapour pressure rises till it becomes equal to the external pressure.
- If the liquid has a low vapour pressure, it has a higher boiling point.
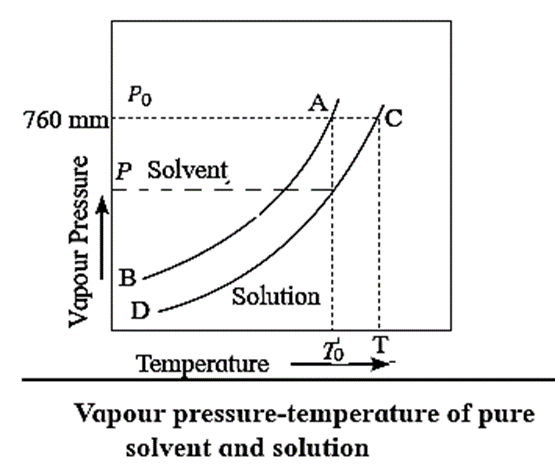
To understand the elevation of boiling point, let us compare the vapour pressures of solution and those of pure solvent. The vapour pressures of solution and of pure solvent are plotted as a function of temperature as shown in Fig.
When a nonvolatile solute is added to a solvent, its vapour pressure decreases, hence the boiling point increases.
If T0 and T are the boiling points of a pure solvent and a solution, then the elevation in the boiling point is given by,
ΔTb = T — T0
The curve AB, represents the variation in the vapour pressure of a pure solvent with temperature while curve CD represents the variation in the vapour pressure of the solution.
This elevation in the boiling point is proportional to the lowering of the vapour pressure, i.e., P0—P, where P0 and P are the vapour pressures of the pure solvent and the solution. [ΔTb ∝ (P0—P) or ΔTb ∝ ΔP]
Boiling point elevation and concentration of solute : The boiling point elevation is directly proportional to the molality of the solution. Thus,
ΔTb ∝ m or ΔTb = Kbm
where m is the molality of solution. The proportionality constant Kb is called boiling point elevation constant or molal elevation constant or ebullioscopic constant.
If m = 1, ΔTb = Kb
Thus, ebullioscopic constant is the boiling point elevation produced by 1 molal solution.
Units of Kb : Kb = ΔTb/m = K/mol kg-1= K kg mol-1 (or 0C kg mol-1)
Therefore, molal elevation constant is the elevation in boiling point produced by 1 molal solution of a nonvolatile solute.
Relation between molar mass of the solute and boiling point elevation :
The boiling point elevation, ΔTb of a solution is directly proportional to molality (m) of the solution. ΔTb ∝ m
ΔTb = Kbm
where Kb is a proportionality constant
If m = 1 molal, then
K ΔTb = Kb.
where K is called molal elevation constant.
The molality of the solution is given by,
m = \(\frac{\text{ Number of moles of the solute}}{\text{Weight of the solvent in kg}}\)
Let W1 = Weight (in gram) of a solvent,
W2 = Weight (in gram) of a solute
M2 = Molecular weight of the solute
Then the molality (m) of the solution is given by
m = \(\frac{W_2×1000}{W_1M_2}=\frac{W_2}{W_1M_2}\) mol kg−1
∴ ΔTb = Kb x \(\frac{W_2×1000}{W_1M_2}\)
∴ M2 = \(\frac{K_bW_2×1000}{ΔT_bW_1M_2}\) or M2 = \(\frac{K_bW_2}{ΔT_bW_1M_2}\) mol kg−1
If the weights and molecular weight are expressed in kg, then,
∴ ΔTb = Kb x \(\frac{W_2}{W_1M_2}\)
Molal elevation constant (Ebullioscopic constant) : It is defined as the elevation in boiling point, produced by dissolving one mole of a solute in 1 kg (or 1000 gram) of a solvent (i.e. 1 molal solution).
The elevation in the boiling point,
ΔTb is given by
ΔTb = Kb x m
where Kb is molal elevation constant and m is molality of the solution.
When m =1, ΔTb = Kb
- Kb depends only on the nature of the solvent.
- Kb does not depend on the nature of the solute.
- It does not depend on concentration of the solution.
The units of molal elevation constant are : (A) K kg mol−1 and (B) K m−1
Depression in freezing point :
Freezing point of a liquid : The freezing point of a liquid is defined as the temperature at which the solid coexists in the equilibrium with the liquid and the vapour pressure of the liquid and the solid are equal.
Depression in the freezing point of a solution : The depression in the freezing point of a solution is defined as the difference between the freezing points of a pure solvent and that of the solution.
If T0 and T are the respective freezing points of a pure solvent and a solution, then the depression in the freezing point ΔTf is given by,
ΔTf = T0 — T (….T < T0)
The depression in the freezing point (ΔTf) is a colligative property.
Freezing point depression as a consequence of vapour pressure lowering :
The effect of dissolution of a nonvolatile solute into a solvent on freezing point of solvent can be understood in terms of the vapour pressure lowering.
The freezing point of a liquid is the temperature at which the liquid and the solid have the same vapour pressure.
Addition of a nonvolatile solute to a liquid decreases the freezing point, i.e. the freezing point of the solution is less than that of the pure solvent.
This is due to the lowering of the vapour pressure of the solvent by the addition of the nonvolatile solute.
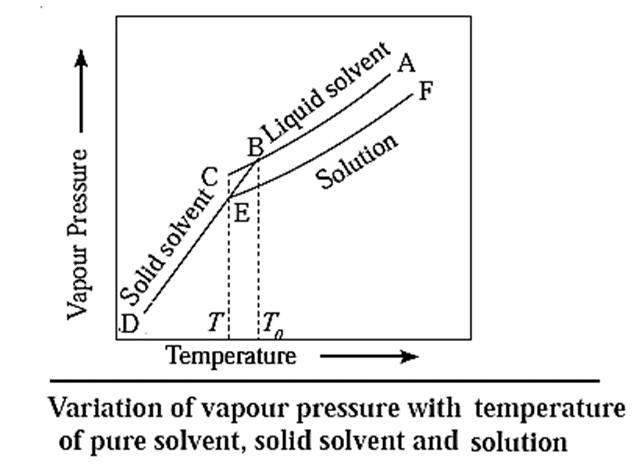
When a liquid is cooled from the point A, its vapour pressure decreases and at the point B, it freezes (solidifies).
In case of a solution, since the vapour pressure is lowered, the freezing point decreases. Hence, if the solution is cooled from the point F, it freezes at lower temperature E, than the pure liquid. This is also due to separation of solvent molecules due to solute molecules decreasing their intermolecular attraction.
If T0 and T are the freezing points of a pure solvent and the solution, then, the depression in the freezing point is given by,
ΔTf = T0 — T.
This depression ΔTf depends on the lowering of the vapour pressure (P0 — P)
ΔTf ∝ (P0 — P),
where P0 and P are the vapour pressures of the pure liquid and the solution.
Freezing point depression and concentration of solute :
As verified experimentally for a dilute solution the freezing point depression (ΔTf) is directly proportional to the molality of solution. Thus,
ΔTf ∝ m or ΔTf = Kf m
where m is the molality of the solution, Kf is a constant of proportionality.
If m = 1 molal,
ΔTf = Kf. Hence Kf is called the cryoscopic constant or molal depression constant. Kf is characteristic of the solvent.
Cryoscopic constant Kf (or molal depression constant) : Molal depression constant is defined as the depression in freezing point, produced by dissolving one mole of a solute in 1 kg (or 1000 g) of a solvent (i.e. 1 molal solution).
Unit of Kf : ΔTf/m = (K or 0C)/(mol kg-1)= K kg mol-1 or 0C kg mol-1
Relationship between freezing point depression of a solution containing non-volatile nonelectrolyte and its molar mass :
The freezing point depression, ΔTf of a solution is directly proportional to molality (m) of the solution.
ΔTf ∝ m
ΔTf = Kf m
where Kf is a molal depression constant.
The molality of a solution is given by,
m = \(\frac{\text{ Number of moles of the solute}}{\text{Weight of the solvent in kg}}\)
If W1 grams of a solvent contain W2 grams of a solute of the molar mass M2, then the molality m of the solution is given by,
m = \(\frac{W_2×1000}{W_1M_2}=\frac{W_2}{W_1M_2}\) mol kg−1
∴ ΔTf = Kf x \(\frac{W_2×1000}{W_1M_2}\)
∴ M2 = \(\frac{K_fW_2×1000}{ΔT_fW_1M_2}\) or M2 = \(\frac{K_fW_2}{ΔT_fW_1M_2}\) mol kg−1
If the weights and molecular weight are expressed in kg, then,
∴ ΔTf = Kf x \(\frac{W_2}{W_1M_2}\)
The unit of Kf is K kg mol-1 .
Hence, from the measurement of the depression in the freezing point of the solution, the molar mass of the substance can be determined.
Osmotic pressure :
Besides the boiling point elevation and freezing point depression, the osmotic pressure is associated with vapour pressure lowering and can be used to determine molar masses of dissolved solutes.
Permeable membrane : A membrane which allows free transfer of the solute molecules from a solution of a higher concentration to a solution of a lower concentration through it is called a permeable membrane and the transfer is called diffusion, e.g., a membrane of a paper.
Semipermeable membrane : A membrane which allows free passage of only the solvent molecules but not the large solute molecules or ions of large molecular mass from a solution of a lower concentration (or a pure solvent) to a solution of higher concentration through it, is called a semipermeable membrane, e.g. parchment paper, complex like Cu2[Fe (CN)6], etc.
Osmosis : It is defined as the net spontaneous flow of solvent molecules into the solution or from more dilute solution to more concentrated solution through a semipermeable membrane is called osmosis.
Consider a vessel divided into two compartments by a semipermeable membrane.
When one compartment is filled with a pure solvent or a dilute solution and another by concentrated solution, there is a spontaneous flow of solvent molecules to the concentrated solution. This arises due to higher vapour pressure of a pure solvent or dilute solution than concentrated solution.
Example : A flow of water molecules from a dilute solution into a concentrated glucose solution through a parchment paper.
Osmotic pressure : The osmotic pressure is defined as the excess mechanical pressure required to be applied to a solution separated by a semipermeable membrane from pure solvent or a dilute solution to prevent the osmosis or free passage of the solvent molecules at a given temperature. The osmotic pressure is a colligative property.
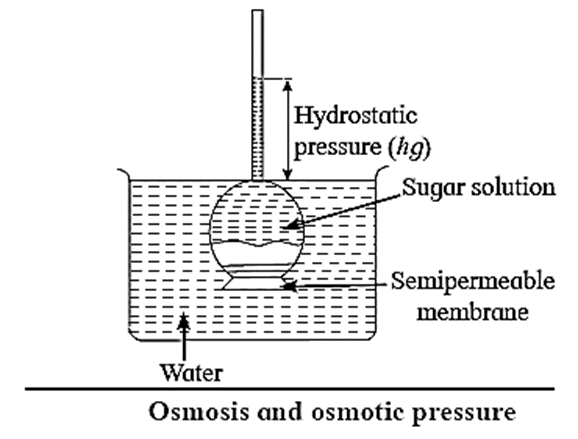
Osmosis can be demonstrated with experimental set up shown in Fig.
- Consider an inverted thistle funnel on the mouth of which a semipermeable membrane is firmly fastened.
- It is filled with the experimental solution and immersed in a solvent like water.
- As a result, solvent molecules pass through the membrane into the solution in the funnel causing rising of level in the arm of thistle funnel.
- This increases the hydrostatic pressure.
- At a certain stage this rising level stops indicating an equilibrium between the rates of flow of solvent molecules from solvent to solution and from solution to solvent. The hydrostatic pressure at this stage represents osmotic pressure of the solution in the thistle funnel.
Remember : It is important to note that osmotic pressure is not the pressure produced by a solution. It exists only when the solution is separated from the solvent by a suitable kind of semipermeable membrane.
Relation between osmotic pressure and concentration of solution :
Consider V dm3 of a solution in which n1 moles of a solvent contains n2 moles of a nonvolatile solute at absolute temperature T.
The osmotic pressure, p of a solution is given by,
π = nRT/V
R is gas constant having value 0.08206 dm3 atm K-1 mol-1 (OR L atm K-1 mol-1). Since concentration, C of a solution is in mol dm-3 or molarity is,
C = n/V mol dm-3 or M
∴ π = CRT, (If concentration C is expressed in mol m-3 and R = 8.314 J K-1 mol-1, then π will be in SI units, pascals or Nm-2.)
- Measurements of osmotic pressure are made at a certain constant temperature.
- Molality depends upon temperature but molality is independent of temperature.
- Hence in osmotic pressure measurements, concentration is expressed in molarity.
Relation between osmotic pressure and molar mass of a solute :
Consider V dm3 (litres) of a solution containing W2 mass of a solute of molar mass M2 at a temperature T.
Number of moles of solute, n2 = W2/M2
The osmotic pressure p is given by,
π = \(\frac{W_2RT}{M_2V}\)
∴ \(M_2=\frac{W_2RT}{πV}\)
By measuring osmotic pressure of a solution, the molar mass of a solute can be calculated.
Since osmotic pressure can be measured more precisely, it is widely used to measure molar masses of the substances
Isotonic solutions : The solutions having the same osmotic pressure at a given temperature are called isotonic solutions.
Explanation : If two solutions of substances A and B contain nA and nB moles dissolved in volume V (in dm3) of the solutions, then their concentrations are,
CA = nA/V (in mol dm-3) and CB = nB/V (in mol dm-3)
If the absolute temperature of both the solutions is T, then by the van’t Hof equation,
πA = CART and pB = CBRT, where πA and πB are their osmotic pressures.
For the isotonic solutions,
πA = πB
∴ CA = CB
∴ nA/V = nB/V
∴ nA = nB
Hence, equal volumes of the isotonic solutions at the same temperature will contain equal number of moles (hence, equal number of molecules) of the substances.
Hypotonic solutions : When two solutions have different osmotic pressures, then the solution having lower osmotic pressure is said to be a hypotonic solution with respect to the other solution.
Explanation : Consider two solutions of the substances A and B having osmotic pressures πA and πB. If πB is less than πA, then the solution B is a hypotonic solution with respect to the solution A.
Hence, if CA and CB are their concentrations, then, CB < CA. Hence, for equal volumes of the solutions, nB < nA.
Hypertonic solutions : When two solutions have different osmotic pressures, then the solution having higher osmotic pressure is said to be a hypertonic solution with respect to the other solution.
Explanation : Consider two solutions of substances A and B having osmotic pressures πA and πB. If pB is greater than πA, then the solution B is a hypertonic solution with respect to the solution A.
Hence, if CA and CB are their concentrations, then, CB > CA. Hence, for equal volumes of the solutions, nB > nA.
Reverse osmosis : osmosis is a flow of solvent through a semipermeable membrane into the solution. The direction of osmosis can be reversed by applying a pressure larger than the osmotic pressure.
The phenomenon of the passage of solvent like water under high pressure from the concentrated aqueous solution like sea water into pure water through a semipermeable membrane is called reverse osmosis.
The osmotic pressure of sea water is about 30 atmospheres. Hence when pressure more than 30 atmospheres is applied on the solution side, regular osmosis stops and reverse osmosis starts. Hence pure Water from sea water enters the other side of pure water.
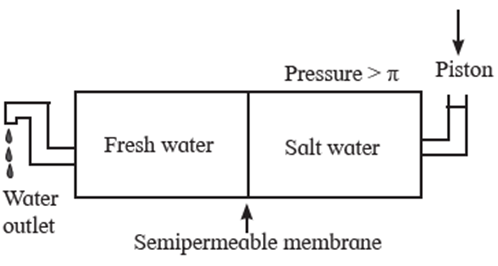
For this purpose a suitable semipermeable membrane is required which can withstand high pressure conditions over a long period.
This method is used successfully in Florida since 1981 producing more than 10 million litres of pure water per day.
Remember : Osmotic pressure is much larger and therefore more precisely measurable property than other colligative properties. It is therefore, useful to determine molar masses of very expensive substances and of the substances that can be prepared in small quantities.
Collgative properties of electrolytes : The study of colligative properties of electrolytes, however, require a different approach than used for colligative properties of nonelectrolytes.
Following are the experimental observations for the colligative behavior of electrolytes.
- The electrolytic solutions do not exhibit colligative properties similar to nonelectrolytes.
- The colligative properties of electrolytes are higher than those shown by equimolar solutions of nonelectrolytes.
- The molar masses of electrolytes determined by colligative properties are found to be considerably lower than their actual molar masses.
Q.Why are the colligative properties of electrolytic solutions greater than those for nonelectrolytic solutions with same concentration ?
Ans. The electrolytes in polar solvents or aqueous solutions dissociate into two or more ions whereas nonelectrolytes do not dissociate.
Consequently the number of particles in electrolytic solutions are considerably higher than equimolar nonelectrolytic solutions.
Therefore the colligative properties of electrolytes are greater than nonelectrolytes with same concentration in solution.
Abnormal colligative property : When the experimentally measured colligative property of a solution is different from that calculated theoretically by the van’t Hoff equation or by the laws of osmosis, then the solution is said to have abnormal colligative property.
Explanation :
- The colligative property depends on the number of solute particles in the solution but it is independent of their nature. Abnormal values of them arise when the dissolved solute undergoes a molecular change like dissociation or association in the solution.
- The observed colligative property (or abnormal colligative property) may be higher or lower than the theoretical value.
Dissociation of the solute molecules: When a solute like an electrolyte is dissolved in a polar solvent like water, it undergoes dissociation, which results in the increase in the number of particles in the solution.
Hence, the observed value of the colligative property becomes higher than the theoretical value, e. g. when one mole of KCI is dissolved in the solution then due to dissociation, KCl —> K+ + Cl-, the number of particles increases, hence, the colligative properties like osmotic pressure, elevation in the boiling point, etc. increase.
Association of the solute molecules: When a solute like a nonelectrolyte is dissolved in a nonpolar solvent like benzene, it undergoes association forming molecules of higher molecular mass. Hence, the number of particles in the solution decreases. Therefore the colligative properties like osmotic pressure, elevation in the boiling point, etc., are lower than the theoretical value.
e.g. nA —> An. 2CH3COOH -> (CH3COOH)2
Abnormal osmotic pressure : When the experimentally observed osmotic pressure is different than theoretically calculated value by van’t Hoff’s equation, then it is called abnormal osmotic pressure.
This arises when the dissolved solute undergoes a molecular change like association or dissociation.
Abnormal molecular masses : When the observed molecular masses obtained from their colligative properties of the substances are different (higher or lower) than the theoretical or normal values calculated from their molecular formulae, then they are called abnormal molecular masses.
Van’t Hoff factor : To obtain the colligative properties of electrolyte solutions by using relations for nonelectrolytes, van’t Hoff suggested a factor i.
It is defined as a ratio of the observed colligative property of the solution to the theoretically calculated colligative property of the solution without considering molecular change.
The van’t Hoff factor can be represented as,
This colligative property may be the lowering of vapour pressure of a solution, the osmotic pressure, the elevation in the boiling point or the depression in the freezing point of the solution. Hence,
\(i=\frac{\text{Observed lowering of vapour pressure}}{\text{Theoretical lowering of vapour pressure}}\)
= ΔP(ob)/ΔP(th)
\(i=\frac{\text{Observed elevation in boiling point}}{\text{Theoretical elevation in boiling point}}\)
= ΔTb(ob)/ΔTb(th)
\(i=\frac{\text{Observed depression in freezing point}}{\text{Theoretical depression in freezing point}}\)
= ΔTf(ob)/ΔTf(th)
\(i=\frac{\text{Observed osmotic pressure}}{\text{Theoretical osmotic pressure}}\)
= π(ob)/ π(th)
- When the solute neither undergoes dissociation or association in the solution, then, i = 1
- When the solute undergoes dissociation in the solution, then, i > l
- When the solute undergoes association in the solution, then i < 1
From the value of the van’t Hoff factor, the degree of dissociation of electrolytes, degree of association of nonelectrolytes can be obtained.
van’t Hoff factor gives the important information about the solute molecules in the solution and chemical bonding in them.
van’t Hoff factor related to molecular mass of the substance :
The van’t Hoff factor is also defined as,
\(i=\frac{\text{Actual moles of particles in solution after dissociation }}{\text{Moles of formula units in dissolved solution}}=\frac{M_{th}}{M_{ob}}\)
In case of nonelectrolytes, i < 1.
In case of electrolytes, i > 1. For example for KNO3 and NaCl, i = 2, for Na2SO4, CaCl2, i = 3, etc.
Modification of expressions of colligative properties : The expressions of colligative properties mentioned earlier for nonelectrolytes are to be modified so as to make them applicable for electrolyte solutions.
The modified equations are:
By Raoult’s law :
\(\frac{P_0-P}{P} = ix_2 = i× \frac{W_2M_1}{W_1M_1}\)
For elevation in boiling point :
ΔTb = i x Kb x m = i x Kb x \(\frac{W_2x1000}{W_1M_1}\)
ΔTb = i x Kb x \(\frac{W_2}{W_1M_1}\)
For depression in freezing point
ΔTf = i x Kf x m = i x Kf x \(\frac{W_2×1000}{W_1M_1}\)
ΔTf = i x Kf x \(\frac{W_2}{W_1M_1}\)
For Osmotic pressure :
π = iCRT =\(i×\frac{WRT}{MV}\)
Relationship between degree of dissociation of an electrolyte and van’t Hoff factor :
Consider 1 dm3 of a solution containing m moles of an electrolyte AxBy. The electrolyte on dissociation gives x number of Ay+ ions and y number of Bx- ions.
Let a be the degree of dissociation.
At equilibrium,
AxBy ⇔ xAy+ + yBx-
For 1 mole of electrolyte : 1 − α, xα, yα
and For ‘m’ moles of an electrolyte : m(1 − α), mxα, myα are the number of particles.
Total number of moles at equilibrium, will be,
Total moles = m(1 − α) + mxα + myα
= m[(1 − α) + xα + yα]
= m[1 + xα + yα − α]
= m[1 + α(x + y − 1)]
The van’t Hoff factor i will be,
\(i=\frac{\text{Observed colligative property}}{\text{Theoretical colligative property}}\)
∴\(i=\frac{m[1 + α(x + y − 1)]}{m}\)
i = 1 + α(x + y − 1)
If total number of ions from one mole of electrolyte is denoted by n, then (x + y) = n
∴ i = 1 + α(n − 1)
∴α(n − 1) = i − 1
∴ α = \(\frac{i-1}{n-1}\) …..(1)
This is a relation between van’t Hoff factor i and degree of dissociation of an electrolyte.
Relation between van’t Hoff factor and molar mass of electrolyte :
Consider an elctrolyte AxBy that dissociates in aqueous solution as
AxBy ⇔ xAy+ + yBx-
Initially : 1 0 0
At equilibrium : (1-∝) (x∝) (y∝)
If i is van’t Hoff factor and n is total number of ions produced from dissociation of one mole of electrolyte then, the degree of dissociation ∝ is given by,
∝ = \(\frac{i-1}{n-1}\)
Now if Mth and Mob are theoretical and observed molecular (or molar) masses respectively, then,
∴ ∝(n — 1) = i – 1 = \(\frac{M_{th}}{M_{ob}}-1\)
∴ ∝(n — 1) =\(\frac{M_{th}-M_{ob}}{M_{ob}}\)
∴ ∝ a = \(\frac{1}{n-1}[\frac{M_{th}-M_{ob}}{M_{ob}}]\) ….. (2)
This is a relation between degree of dissociation and molecular masses of the dissolved electrolyte AxBy
Q. Arrange the following solutions in order of increasing osmotic pressure. Assume complete ionization. a) 0.5m Li2SO4 b) 0.5m KCl c) 0.5m Al2(SO4)3 d) 0.1m BaCl2.
Consider 1 dm3 of each solution. a) 0.5m Li2SO4 (a) Li2SO4 --> 2Li+ + SO42- (Total particles =2x0.5+0.5=1.5m) b) 0.5m KCl KCl --> K+ + Cl- (Total particles =0.5+0.5=1m) c) 0.5m Al2(SO4)3 Al2(SO4)3 --> 2Al3+ + 3SO42- (Total particles =2x0.5+3x0.5=1+1.5=2.5m) d) 0.1m BaCl2. BaCl2 --> Ba2+ + 2Cl- (Total particles =0.1+2x0.1=0.1+0.2=0.3m) Osmotic pressure being a colligative properly, it depends on number of particles in the solution. Therefore, increasing order of osmotic pressure is, BaCl2 < KCl < Li2SO4 < Al2(SO4)3 03m 1m 1.5m 2.5m
We reply to valid query.