Electrostatics
Maharashtra Board-Class-12th-Physics-Chapter-8
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Gauss’ Law : The flux of the net electric field through a closed surface equals the net charge q enclosed by the surface divided by ε0
Φ = \(\oint \vec{E}.\vec{ds}=\frac{q}{ε_0}\)
where Φ is the total flux coming out of a closed surface
q is the total charge inside the closed surface.
ε0 is the permittivity of free space and the electric flux.
\(\vec{E}.\vec{ds}\) is integrated over the entire area of the surface.
- Gauss’Law gives the relationship between the electric charge and its electric field.
- It also provides equivalent methods for finding electric field intensity.
Common steps involved in calculating electric field intensity by using Gauss’ theorem :
Gauss/s law simplifies the calculation of the electric field at a point due to an extended charged object of certain symmetry.
- To find the electric field at a point, take that point on a Gaussian surface
- Use a Gaussian surface, either having the same symmetry as the charged object or in the form of a small cylinder suitably oriented, such that \(\vec{E}\) at every point on the surface is constant in magnitude and is parallel or perpendicular to \(\vec{ds}. This simplifies the calculation of the integral, which is now equal to the magnitude | | times the total area of the Gaussian surface; call this product as A.
- Find the total charge enclosed by the Gaussian surface—algebraic sum of the charges for discrete charges or in terms of charge density for continuous distribution of charges. Divide this net charge by ε0 and call it B.
- Equate A and B to calculate the magnitude of the electric field, |\(\vec{E}\) |.
Q. A Gaussian surface in the form of a cube is centred on a point charge Q. What is the flux through one face of the cube ?
Ans. Since the point charge is at the centre of the cube, the electric flux through each face is the same. Therefore, the electric flux through one face is 1/6 th of the electric flux originating from or terminating at the point charge. If ε is the permittivity of the medium, the electric flux through one face = Q/6ε
Applications of Gauss’s law
Electric Field Intensity due to Uniformly Charged Spherical Shell or Hollow Sphere: Consider an isolated charged hollow spherical conductor A, of radius R and surface charge density σ, placed in a medium of permittivity ε. Consider a point P outside the conductor at a distance r from its centre. To find the electric field intensity at P, we choose a spherical Gaussian surface S of radius r through P and concentric with conductor A. A small element of this surface containing P has an area dS. The charge on the sphere is Q = σ (4πR2) …..(1) The charge Q is uniformly distributed over the outer surface of the spherical conductor. Then, by symmetry, the electric field intensity at every point on surface S is normal to the surface and has the same magnitude E. If charge Q is positive, \(\vec{E}\) at every point on S is radially outward. The angle θ between \(\vec{E}\) and \(\vec{ds}\) being zero for every surface element, the electric flux throughevery element is dΦ = \(\vec{E}.\vec{ds}\). = E Therefore, the flux through the Gaussian surface S is Φ = \(\oint E.ds\) = (E \oint ds\) ...(2) \(\oint ds\) = surface area of the sphere = 4πR2 ∴ Φ = E x 4πr2 (3) Then, by Gauss’s theorem, Φ = Q/ε = E x 4πr2 ...(4) ∴ E = \(\frac{Q}{4πεr^2}=\frac{Q}{4πε_0kr^2} \) ……..(5) where ε0 is the permittivity of free space and k = ε/ε0 is the relative permittivity (dielectric constant) of the surrounding medium. ∴ E = \(\frac{σ(4πεR^2)}{4πεr^2} \)= \(\frac{σR^2}{εr^2} \) ……..(6) Equations (5) and (6) give the magnitude of the electric field intensity at a point P outside a hollow spherical conductor. If the net charge Q enclosed by the Gaussian surface is positive, is radially outward; if Q is negative, F is radially inward. Equation (5) shows that for a point outside a hollow spherical conductor carrying a charge Q, the conductor behaves like a point charge Q at its centre. Case (1) electric intensity on the surface of (i.e., just outside) the spherical conductor: At a point just outside the sphere, r ≈ R ∴ E = σ/ε = σ/kε0 Case (2) electric intensity inside the spherical conductor: Since electric charge resides on the outer surface of a hollow conductor, the charge inside the hollow spherical conductor σ is zero. Then, Einside = 0.

| Know This :
Electric flux, or the number of electric field lines, passing through the Gaussian surface is independent of the size of the Gaussian surface. It depends on the number of field lines originating from or terminating at the point charge, which in turn depends on the magnitude of the point charge and the permittivity of the medium. |
Electric Field Intensity due to an Infinitely Long Straight Charged Wire: Consider a uniformly charged wire of infinite length having a constant linear charge density λ (charge per unit length), kept in a medium of permittivity ε (ε = ε0k ) . To find the electric field intensity at P ,at a distance r from the charged wire, imagine a coaxial Gaussian cylinder of length l and radius r (closed at each end by plane caps normal to the axis) passing through the point P. As λ is the charge per unit length of conductor A, the net charge enclosed by the Gaussian cylinder of length l is Q = λl ……..(1) Consider a very small area ds at the point P on the Gaussian surface. Charge is uniformly distributed over the outer surface of the cylindrical conductor. Then, by symmetry, the electric field intensity at any point outside the conductor is perpendicular to the cylinder axis. Hence, the component of the electric field intensity perpendicular to the plane circular faces of the Gaussian surface is zero. Therefore, the electric flux through these flat faces is zero. By symmetry, the electric field intensity \(\vec{E}\) at every point on the curved face of surface S is normal to the surface and has the same magnitude E. If the charge on conductor A is positive, \(\vec{E}\) is directed along the outward drawn normal \(\vec{ds}\). The angle θ between \(\vec{E}\) and \(\vec{ds}\) being zero for every surface element, the electric flux through every element is dΦ = \(\vec{E}.\vec{ds}\) = E ds Therefore, the flux through the curved face of the Gaussian surface S is Φ = \(\oint E.ds\) = \(E\oint ds\) ...(2) \(E\oint ds\)= area of the curved surface = 2πrl, where l is the length of the cylinder as shown in the figure. ∴ Φ = E x 2πrl ...(3) Then, by Gauss’s theorem, Φ = Q/ε = E x 2πrl ...(4) ∴ E = \(\frac{λl}{ε(2πrl)}\)=\(\frac{λ}{2πεr}\)= \(\frac{λ}{2πε_0kr}\) ……….(5) where ε0 is the permittivity of free space and k = ε/ε0 is the relative permittivity (dielectric constant) of the surrounding medium. This gives the magnitude of the electric field intensity in terms of the linear charge density λ. For positive λ, \(\vec{E}\) is outward, while for negative λ, \(\vec{E}\) is inward. Remember : (1) If σ is the surface charge density (charge per unit area), σ = \(\frac{λl}{2πRl}\) = \(\frac{λ}{2πR}\) ∴ λ = 2πRσ ∴ E =\(\frac{2πRσ}{2πε_0kr}=\frac{Rσ}{ε_0kr} \) (2) If the charge on the conductor is negative, \(\vec{E}\) is inward


Expression for kinetic energy :
Let r be the radius of the uniform circular motion of the electron. The electric field intensity at every point on the circular path is radially outward and has the same magnitude E = \(\frac{λ}{2πεr}\)
∴ The centripetal force on the electron,
Fc = \(\frac{m_ev^2}{r}\)= eE = \(\frac{eλ}{2πεr}\)
where me and v are the mass and linear speed of the electron.
∴ mev2 = \(\frac{eλ}{2πε}\)
∴ The kinetic energy of the electron,
½ mev2 = \(\frac{eλ}{4πε}\)
Electric Field due to a Charged Infinite Plane Sheet:
Consider a uniformly charged infinite plane sheet with surface charge density σ.
By symmetry electric field is perpendicular to plane sheet and directed outwards, having same magnitude at a given distance on either sides of the sheet. Let P be a point at a distance r from the sheet and E be the electric field at P.

To find E at a point P outside the sheet, imagine a Gaussian surface in the form of a small closed cylinder. Its axis is perpendicular to the sheet, with the point P on one end face, see above Fig.
The cylinder encloses a small area dS of the sheet. So, the charge enclosed by the cylinder = σdS ……(1)
The flux through one end = EdS
The flux through the Gaussian surface,
Φ = 2EdS ……(2)
By Gauss’s theorem,
εΦ = net charge enclosed
ε(2EdS) = σdS ……(3)
∴ E = σ/2ε = σ/2kε0 ……(4)
where ε0 is the permittivity of free space and k = ε/ε0 is the relative permittivity (dielectric constant) of the surrounding medium.
Equation (4) shows that the magnitude of the electric field intensity outside the charged sheet is uniform and independent of the distance from the sheet.
Remember :
(1) The electric field lines are straight, parallel to each other, and perpendicular to the sheet.
(2) If the sheet is negatively charged, \(\vec{E}\) on either side of the sheet is directed towards the sheet.
Expression for force per unit area on a charged conductor : Consider a positively charged conductor of any shape placed in a dielectric medium of permittivity ε Let dS be a very small area of the surface of the conductor drawn around point A as shown in the figure. If σ is the surface charge density on dS, the charge on the area element is σdS and the electric field intensity at a point just outside the area element has a magnitude E = σ/ε, \(\vec{E}\) can be considered as a resultant of : (i) \(\vec{E_1}\) due to the charge on the area dS and (ii) \(\vec{E_2}\) due to the charge on the remaining part of the conductor, i.e., excluding dS. Since the two fields have the same direction, E = E1 + E2 ….(1) \(\vec{E_1}\) has opposite directions on the two sides of dS; but on both sides, \(\vec{E_2}\) is directed along the outward normal to the element. At point B inside the conductor, the electric field is zero. ∴ E2 − E1 = 0 E2 = E1 At A, just outside the conductor E1 + E2 = E ∴ E2 = E1 = ½ E But, E = σ/ε …..(2) ∴ E2 = E1 = σ/2ε …..(3) Thus, the charged area element σdS is situated in an electric field of magnitude E2 = σ/2ε , produced by the charge on the rest of the conductor and this field is outward. The force acting on dS due to the action of this field. = (charge on area dS) x (electric field due to the remaining charge) ∴ F = σdS x E2 = \(σdS×\frac{σ}{2ε}=\frac{σ^2}{2ε}dS\) …..(4) This force acts outward, normal to the surface. The magnitude of the mechanical force per unit area of the surface is f = F/ds = \(\frac{σ^2}{2ε}=\frac{σ^2}{2kε_0}\) …..(5) where ε0 is the permittivity of free space and k = ε/ε0 is the relative permittivity of the medium. From Eq. (2), σ = ε E = ε0kE Substituting this value of σ in Eq. (5), f =\frac{(ε_0kE)^2}{2kε_0}\) = \(\frac{1}{2}ε_0kE^2\) Thus, the mechanical force per unit area of a charged conductor, f = \(\frac{σ^2}{2kε_0}\) or f = \(\frac{1}{2}ε_0kE^2\) If the charge on the conductor is negative, the field at any area element will be inward. But charge on the area element being negative, the force on the area element due to will still be outward, normal to the surface, Therefore, the force on the charged area element σdS is F = ½ εE2ds. This force acts outward, normal to the surface.

Expression for work done in displacing a charged area element :
Suppose an external agent displaces the charged area element through a small distance dx in a direction opposite to the above outward force, always keeping the element in equilibrium. To do so, the external agent must apply a force of equal magnitude in the opposite direction. Then, the work done by the external agent against the mechanical force,
dW = Fdx = (½ εE2ds) dx
During the displacement dx, the area element sweeps out a volume, dV= dS.dx.
∴ dW = ½ εE2dV

This work done is stored in the electric field in the medium in the form of potential energy. Therefore, the energy density, i.e., the energy stored per unit volume of the medium is
dW/dV = \(\frac{1}{2}εE^2\) = \(\frac{1}{2}ε_0kE^2\)
Electric Potential and Potential Energy:
Gravitational potential :
We measure the gravitational potential energy U of a body
- (1) by assigning U = 0 for a reference configuration (such as the body at a reference level)
- (2) then equating U to the work W done by an external force to move the body up or down from that level to a point.
We then define gravitational potential of the point as gravitational potential energy per unit mass of the body.
Electrostatic potential energy : Electrostatic potential energy is the work done against the electrostatic forces to achieve a certain configuration of charges in a given system.
Since every system tries to attain the lowest potential energy, work is always required to be done to change the configuration.
Consider a positive charge Q fixed at some point in space. For bringing any other positive charge close to it, work is necessary. This work is equal to the change in the potential energy of their system.
Thus, work done against a electrostatic force = Increase in the potential energy of the system.
∴\(\vec{F}.\vec{dr}\) = dU
where dU is the increase in potential energy when the charge is displaced through \(\vec{dr}\) and \(\vec{F}\) is the force exerted on the charge.
Expression for potential energy:
Consider a test charge qo in the electric field \(\vec{E}\) of a source charge + Q. The electric force acting on the test charge, \(q_0\vec{E}\) , is a conservative force. When the test charge is moved in the field at constant velocity by some external agent, the work done by the field on the charge is equal to the negative of the work done by the external agent causing the displacement. Suppose an external agent moves the test charge without acceleration from a point A, at a distance r1 from + Q, up to a point B, at a distance r2, see Fig.
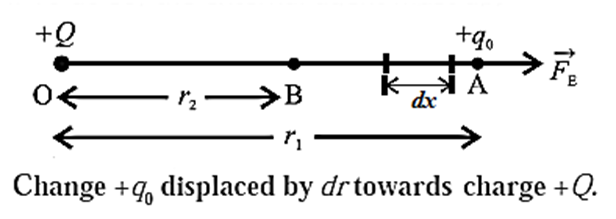
Since the electric field surrounding a point charge is not uniform, the electrostatic force on qo increases as it approaches Q. Consequently, the external agent has to exert on qo a force of increasing magnitude and, for equal displacements, do increasing amount of work. Because the force exerted varies along the path, we imagine the total displacement to be made up of a large number of infinitesimal displacements \(\vec{dx}\) . The distance dx is so small that, at an average distance x from Q, the electrostatic force \(\vec{F}\) on qo has a constant magnitude
F = \(\frac{1}{4πε_0}\frac{Qq_0}{x^2}\)
over the distance dx. The force \(\vec{F_E}\) in by the external agent is equal and opposite to \(\vec{F}\) at every instant : \(\vec{F_E}\) = \(-\vec{F}\)
Therefore, the infinitesimal work dW done by the external agent for the displacement \(\vec{dx}\) is
dW = \(\vec{F_E}.\vec{dx}\) = FE.dx = −Fdx
The total work done by the external agent in moving the test charge from B up to A is the line intergral of dW between the limits x = r1 and x = r2.
W = \(\int_{x=r_1}^{x=r_2}dw=\int_{r_1}^{r_2}(-\frac{1}{4πε_0}\frac{Qq_0}{x^2})dx\)
= \(-\frac{1}{4πε_0}Qq_0\int_{r_1}^{r_2}\frac{dx}{x^2}\)
= \(-\frac{1}{4πε_0}Qq_0[\frac{dx}{x^2}]_{r_1}^{r_2}\)
=\(-\frac{1}{4πε_0}Qq_0[-\frac{1}{r}-(-\frac{1}{r_1})]\)
= \(\frac{1}{4πε_0}Qq_0(\frac{1}{r}-(\frac{1}{r_1})\) = ΔU
where ΔU = UB — UA is the change in the potential energy of the test charge in moving it from the point A to the point B. Choosing the potential energy of qo to be zero when it is infinitely far away from Q, i.e., r1 = ∞, its potential energy at a distance r from Q is
U(r) = \(\frac{1}{4πε_0}\frac{Qq_0}{r}\)
Thus, the potential energy U of the system of two point charges q1 and q2 separated by r can be obtained from the above equation by using r1 = ∞, and r2 = r,. It is then given by,
U(r) = \(\frac{1}{4πε_0}\frac{q_1q_2}{r}\)
Remember : Taking U(∞) =0 is often a convenient reference level in electrostatics, but in circuit analysis other reference levels are often more convenient.
Units of potential energy :
SI unit= joule (J)
“One joule is the energy stored in moving a charge of 1C through a potential difference of 1 volt.
Electron volt : Another convenient unit of energy (Non SI unit) is electron volt (eV), which is the change in the kinetic energy of an electron while crossing two points maintained at a potential difference of 1 volt.”
ΔKE = q ΔV
1 eV = 1.6 × 10-19 joule
Other related units are:
1 meV = 1.6 × 10-22 J
1 kev = 1.6 × 10-16 J
Concept of Potential:
Electric potential : The electric potential V at a point in an electric field is defined as the work per unit charge that must be done by an external agent against the electric force to move without acceleration a sufficiently small positive test charge from infinity to the point of interest.
Concept of electric potential difference :
A charge in an electric field possesses electric potential energy just as a particle in a gravitational field possesses gravitational potential energy.
Consider a test charge qo in an electric field, moved very slowly by an external agent from point B where its electric potential energy is UB to a point A where its electric potential energy is UA.
The change in the potential energy, UA — UB, is defined as the work WB→A that must be done by an external agent to move the test charge from B to A against the electric force, keeping the charge always in equilibrium, i.e., without accelerating the charge so as not to give it any kinetic energy.
WB→A = ΔU = UA − UB
The potential difference ΔV = VAB = VA − VB between two points A and B in electric field is
ΔV = WB→A/q0 = ΔU/ q0
Electric potential difference : The electric potential difference between two points in an electric field is defined as the work done per unit charge by an external agent against the electric force in moving an infinitesimal positive charge from one point to the other without acceleration.
We choose the potential energy UB and potential VB to be zero when the initial point B is infinitely far from the source charges which produce the field,
Then, the work done per unit test charge by an external agent in bringing a test charge from infinity to a point is the electric potential at that point.
The electric potential at a distance r from a source charge,
V(r) = WB→A/q0 = U(r)/ q0
Relation between electric field and electric potential:
Consider a test charge qo as it moves from point A to point B in an electric field. The electric force on qo at any point along the path is
\(\vec{F}\) = \(q_0\vec{E}\) , where \(\vec{E}\) is the field at that point.
The incremental work dW done by the field as qo undergoes a displacement \(\vec{dl}\) along the path is
dW = \(\vec{F}.\vec{dl}\) = \(q_0\vec{E}.\vec{dl}\)= qo E dl
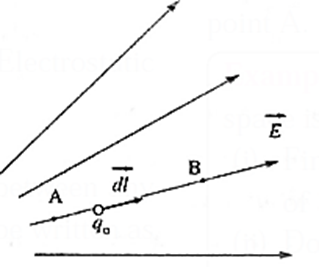
In the process, the charge qo is moved from a higher potential to a lower potential, thereby losing potential energy. Therefore, the change in potential energy
dU = −dW = −qo E dl
By definition, the change in electric potential is
dV = dU/q0
∴ dV = − E dl
∴ E = − dV/dl
If Ex, Ey and EZ are the rectangular components
Ex = − dV/dx , Ey = − dV/dy, Ez = − dV/dz
The quantity dV/dl is the rate at which the electric potential changes with distance and is called the electric potential gradient. The above equation thus shows that the magnitude of the electric field intensity at a point is equal to the negative of the potential gradient at that point.
Electric potential gradient : The rate of change of electric potential with distance in a specified direction is called the electric potential gradient in that direction.
Expression for the electric potential at a point due to an isolated point charge :
Consider a point A at a distance r from a static point charge +Q, as shown in Fig.
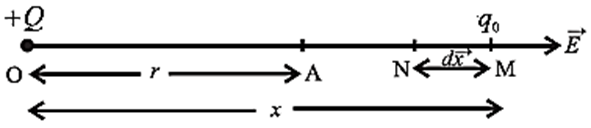
To determine the electric potential at the point A (due to Q), imagine a test charge qo being moved from infinity up to the point A without acceleration. Because the electric field of a point charge is not uniform, the force exerted by Q on qo increases as it approaches Q. We imagine the total displacement to be made up of a large number of infinitesimal displacements \(\vec{dx}\). The distance dx is so small that, at an average distance x from Q, the electrostatic force \(\vec{F}\) on qo has a constant magnitude
F = \(\frac{1}{4πε_0}\frac{q_1q_2}{r}\)
Over the distance dx. The forec FE by the external agent is equal and opposite to \(\vec{F}\) at every instant : \(\vec{F_E}\) =\(-\vec{F}\)
Therefore infinitesimal work dW done by the external agent for the displacement \(\vec{dx}\) is
dW = \(\vec{F_E}.\vec{dx}\) = FE.dx = −Fdx
∴ dW = \(\frac{1}{4πε_0}\frac{q_1q_2}{r}dx\)
The total work done by the external agent in moving the test charge from infinity up to the point A (from x = ∞ to x = r) is the integral of dW between the limits x = ∞ and x = r.
W = \(\int_{x=∞}^{x=r}dw=\int_{∞}^{r}(-\frac{1}{4πε_0}\frac{Qq_0}{x^2})dx\)
= \(-\frac{1}{4πε_0}Qq_0\int_{∞}^{r}\frac{dx}{x^2}\)
= \(-\frac{1}{4πε_0}Qq_0[-\frac{1}{x}]_{∞}^{r}\)
=\(-\frac{1}{4πε_0}Qq_0[-\frac{1}{r}-(-\frac{1}{∞})]\)
=\(-\frac{1}{4πε_0}\frac{Qq_0}{r}\)
= ΔU
where ΔU = UA — U∞ is the change in the potential energy of the test charge in moving it from ∞ to the point A. Choosing the potential energy of q0 to be zero when it is infinitely far away from Q, its potential energy at a distance r from Q is
UA = \(\frac{1}{4πε_0}\frac{Qq_0}{r}\)
Therefore, the electric potential at a distance r from Q is
V = UA/q0 =\(\frac{1}{4πε_0}\frac{Q}{r}\)
The above equation also gives the electric potential either outside or on the external surface of a spherically symmetric charge distribution.
Remember :
- A positive charge produces a positive electric potential. A negative charge produces a negative electric potential.
- A negative electric potential means a positive charge would be attracted from a larger distance, since the potential is lower (more negative) than at larger distances. Conversely, a negative charge would be repelled, as expected.
- Only differences between potentials at two points are physically significant. Potential at a point is ambiguous unless we specify which the reference point is.
- Electric potential, like electric field intensity, is independent of the magnitude of the test charge that we use to define it.
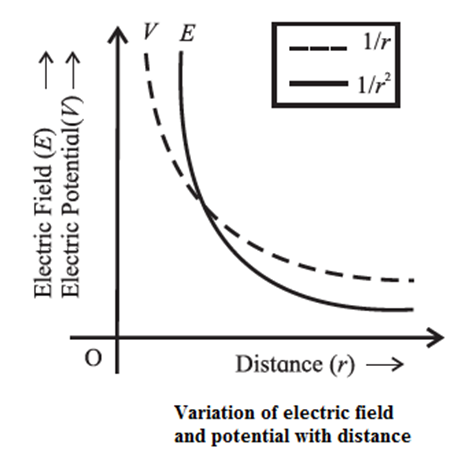
- At a point a distance r from an isolated point charge, the force F on a point charge and the electric field E both vary as 1/r2, while the potential energy U of a point charge and the electric potential V at the point both vary as 1/r.
Electric potential due to an electric dipole:
Consider an electric dipole AB of dipole length 2l and point charges + q and −q. Its electric dipole moment \(\vec{p}\) has magnitude p = 2ql.
Let C be a point at a distance r from O, the centre of the dipole, in a direction θ with the dipole axis, as shown in Fig.
Let AC = r1 and BC = r2.
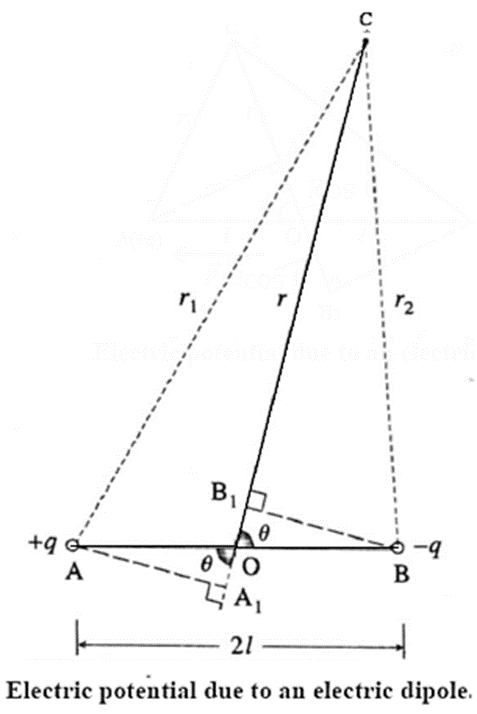
The electric potential at P due to the charge + q is
V1 = \(+\frac{1}{4πε_0}\frac{q}{r_1}\) …..(1)
and that due to the charge −q is
V2 = \(-\frac{1}{4πε_0}\frac{q}{r_2}\) …..(2)
Since potential is a scalar quantity, the resultant electric potential at P due to the dipole is
V= V1 + V2 = \(+\frac{1}{4πε_0}\frac{q}{r_1}\) \(-\frac{1}{4πε_0}\frac{q}{r_2}\)
= \(\frac{q}{4πε_0}(\frac{1}{r_1}-\frac{1}{r_2})\) = \(\frac{q}{4πε_0}(\frac{r_2-r_1}{r_1r_2})\) …..(3)
In the figure, CA1 = CA = r1 and CB1 = CB = r2.
For short dipole (2l << r), ∠OA1A ≅ ∠OB1B ≅ 90°.
Hence, in the right angled Δ OA1A and OB1B,
OA1 = OB1 = lcos θ
r2 — r1 = CA1 − CB1 = A1B1 = 2lcos θ ……(4)
Also, r1 r2 = CA1 x CB1 = (CO + OA1)(CO − OB1)
= (r + lcos θ)(r − lcos θ)
= l2 – l2cos2θ
∴ r1 r2 ≈ r2 (‘.’ l << r) …..(5)
From eq. (3), (4) & (5)
V = \(\frac{q}{4πε_0}(\frac{2lcosθ}{r^2})\)=\(\frac{1}{4πε_0}(\frac{(2ql)cosθ}{r^2})\)
= \(\frac{1}{4πε_0}(\frac{pcosθ}{r^2})\) …..(5)
This is the required expression
Particular cases :
(i) At a point on the dipole axis, θ = 0° (nearer to the charge +q) or 180° (nearer to the charge −q)
Cos θ = ± 1
∴ Vaxis= ±\(\frac{1}{4πε_0}(\frac{pcosθ}{r^2})\)
(ii) At a point on the dipole equator, θ = 90° or 270°.
cos θ = 0 ∴ Vequator = 0
Remember : Since Vequator = 0, the equatorial plane of a dipole is an equipotential plane of electric potential equal to zero. No work is required to move a charge anywhere in the equatorial plane
Electrostatics potential due to a system of charges :
Or
Expression for the electric potential at a point due to several point charges :
Consider a system of charges q1, q2 ......... qn at distances r1, r2 ...... rn respectively from point P. The potential V1 at P due to the charge q1 is
V1 = \(\frac{1}{4πε_0}\frac{q_1}{r_1}\)
Similarly the potentials V2, V3 ........Vn at P due to the individual charges q2, q3 ...........qn are given by
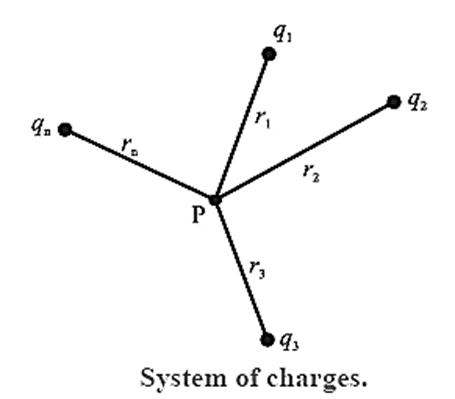
V2 = \(\frac{1}{4πε_0}\frac{q_2}{r_2}\), V3 = \(\frac{1}{4πε_0}\frac{q_3}{r_3}\) , …….. Vn = \(\frac{1}{4πε_0}\frac{q_n}{r_n}\)
By the superposition principle, the potential V at P due to the system of charges is the algebraic sum of the potentials due to the individual charges.
∴ V = V1 + V2 +......+ Vn
= \(\frac{1}{4πε_0}(\frac{q_1}{r_1}+\frac{q_2}{r_2}+....\frac{q_n}{r_n})\)
=\(\frac{1}{4πε_0}\sum_{i=1}^{n}\frac{q_i}{r_i}\)
For a continuous charge distribution, summation should be replaced by integration.
Remember : Electric potential is a scalar quantity. To calculate the resultant potential due to two or more point charges, the potentials due to individual charges are added as simple scalars along with its sign, determined by the sign of the q that produces V
Q. Is electrostatic potential necessarily zero at a point where electric field strength is zero? Justify.
Ans : Electric potential is a scalar quantity while electric field intensity is a vector quantity. When we add potentials at a point due two or more point charges, the operation is simple scalar addition along with the Sign of V, determined by the sign of the q that produces V. At a point, the net field is the vector sum of the fields due to the individual charges. Midway between the two charges of an electric dipole, the potentials due to the two charges are equal in magnitude but opposite in sign, and thus add up to zero. But the electric fields due to the charges are equal in magnitude and direction—towards the negative charge—so that the net field there is not zero. But midway between two like charges of equal magnitudes, the potentials are equal in magnitude and have the same sign, so that the net potential is nonzero. However, the fields due to the two equal like charges are equal in magnitude but opposite in direction, and thus vectorially add up to zero.
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-7-Wave Optics –Online Notes Next Chapter : Chapter-9-Current Electricity – Online Notes
good notes