Coordinate Geometry
Class-10-Mathematics-2-Chapter-5-Maharashtra Board
Notes
|
Topics to be learn
|
Introduction :
How to find the distance between any two points on a number line :
If x1 and x2 are the co—ordinates of points A and B and x2 > x1 then length of
seg AB = d(A,B) = x2 — x1
Example :
If co—ordinates of points P, Q and R are —1,—5 and 4 respectively then find the length of seg PQ, seg QR.
![]()
As shown in the figure, co—ordinates of points P, Q and R are —1,—5 and 4 respectively.
∴ length of seg PQ = d(P, Q) = (—1)—(—5) = —1 + 5 = 4
and length of seg QR = d(Q, R) = 4 — (—5) = 4 + 5 = 9
- Using the same concept, we will understand to find the distance between two points in the XY—plane.
(1) To find distance between any two points on any axis :
(i) To find the distance between any two points on X—axis.
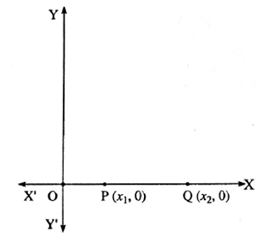
In the figure, points P(x1, 0) and Q(x2, 0) lie on X—axis.
Q lies to the right side of P, ∴ x2 > x1.
∴ d(P, Q) = x2 — x1.
(ii) To find distance between any two points on Y—axis.
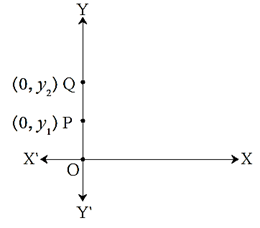
In the figure, points P(0, yl) and Q(0, y2) lie on Y—axis.
The points Q lie above point P, ∴ y2 > y1.
∴ d(P,Q) = y2 — y1
(2) To find the distance between the two points, if the segment joining these points is parallel to any axis in the XY—plane :
(i) In the figure, seg AB is parallel to X—axis.
y—coordinates of points A and B are equal.
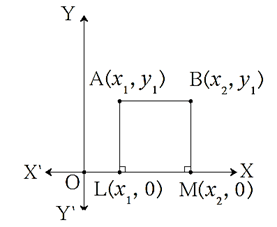
We draw seg AL and seg BM perpendiculér to X—axis.
∴ c ALMB is a rectangle.
∴ AB = LM …(Opposite sides of a rectangle)
as LM = x2 — x1, AB = x2 — x1
(ii) In the figure, seg PQ is parallel to Y—axis.
x—coordinates of points P and Q are equal.
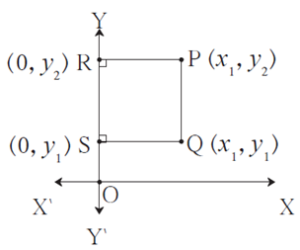
Draw seg PR and seg QS perpendicular to Y axis.
∴ c PQSR is a rectangle
∴ PQ = RS ….(Opposite sides of a rectangle)
But, RS = y2 — y1
∴ d(P,Q) = y2 — y1
Example :
In the figure, seg AB || Y—axis and seg CB || X—axis. Co—ordinates of points A and C are given.
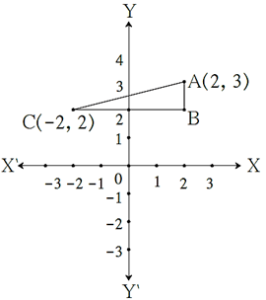
To find AC, fill in the boxes ([ ]) given below.
Δ ABC is a right angled triangle.
According to Pythagoras theorem,
(AB)2 + (BC)2 = [ ]
We will find co—ordinates of point B
to find the lengths AB and BC,
CB || X— axis ∴ y co—ordinate of B = [ ]
BA || Y— axis ∴ x co—ordinate of B = [ ]
AB = [3] — [ ] = [ ], BC = [ ] — [ ] = [ 4 ]
∴ AC2 = [ ] + [ ] = [ ] ∴ AC = [ \(\sqrt{17}\) ]
Solution :
(AB)2 + (BC)2 = [ (AC)2 ]
We will find co—ordinates of point B
to find the lengths AB and BC,
CB || X— axis ∴ y co—ordinate of B = [ 2 ]
BA || Y— axis ∴ x co—ordinate of B = [ 2 ]
AB = [3] — [ 2 ] = [ 1 ], BC = [ 2 ] — [ —2 ] = [4]
∴ AC2 = [ 12 ] + [ 42 ] = [ 17 ] ∴ AC = [ \(\sqrt{17}\) ]
Distance formula :
In the below figure, A(x1, y1) and B(x2, y2) are any two points in the XY plane.
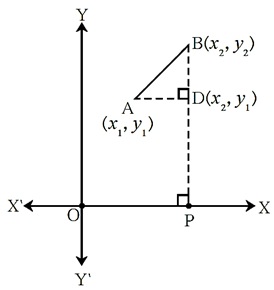
From point B draw perpendicular BP on X—axis.
Similarly from point A draw perpendicular AD on seg BP.
seg BP is parallel to Y—axis.
∴ the x co—ordinate of point D is x2.
seg AD is parallel to X—axis.
∴ the y co—ordinate of point D is y1.
∴ AD =d(A, D) = x2 — x1 ; BD= d(B, D) = y2 — y1
In right angled triangle Δ ABD,
AB2 = AD2 + BD2 = ( x2 — x1 )2 + ( y2 — y1 ) 2
∴ AB = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
This is known as distance formula.
Note that, \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\) = \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)
Example :
(i) In the figure, seg AB || Y—axis and seg CB || X—axis. Co—ordinates of points A and C are given. Find lengths of seg AB seg AC and seg BC.
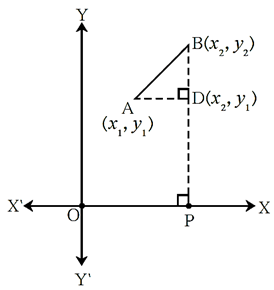
Solution :
Seg AB || Y—axis and seg BC || X—axis.
∴ Co—ordinates of point B are (2, 2).
Co—ordinates of point A(2, 3) and C(—2, 2) is given
(a) Find length of seg AB :
Co—ordinates of point A(2, 3) and B(2, 2)
By distance formula
AB = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
∴ AB = \(\sqrt{(2-2)^2+(2-3)^2}\) = \(\sqrt{(0)^2+(-1)^2}=\sqrt{1}\) = 1
(b) Find length of seg AC :
Co—ordinates of point A(2, 3) and C(—2, 2)
By distance formula
AC = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
∴ AC = \(\sqrt{(-2-2)^2+(2-3)^2}\) = \(\sqrt{(-4)^2+(-1)^2}=\sqrt{16+1}\) = \(\sqrt{17}\)
(c) Find length of seg BC :
Co—ordinates of point B(2, 2) and C(—2, 2)
By distance formula
BC = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
∴ BC = \(\sqrt{(-2-2)^2+(2-2)^2}\) = \(\sqrt{(-4)^2+(0)^2}=\sqrt{16}\) = 4
| To be Remember :
Coordinates of origin are (0, 0). Hence if coordinates of point A are (x, y), then d(OA) = \(\sqrt{x^2+y^2}\) If points A(x1, y1), B(x2, y2) lie in the XY—plane. then d(A, B) = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\) that is, AB2 = ( x2 — x1 )2 + ( y2 — y1 ) 2 = ( x1 — x2 )2 + ( y1 — y2 ) 2 |
| Recall :
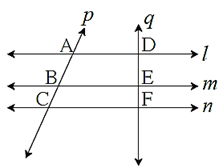
Property of intercepts made by three parallel lines :
In the figure line l || line m || line n, line p and line q are transversals, then \(\frac{AB}{BC}=\frac{DE}{EF}\) |
Division of a line segment :
![]()
In the figure, AP = 6 and PB = 10. ∴ \(\frac{AP}{PB}=\frac{6}{10}=\frac{3}{5}\)
∴ We can say that, point P divides the line segment AB in the ratio 3 : 5.
Section formula :
In the figure, point P on the seg RS in XY-plane, divides seg RS in the ratio m : n.
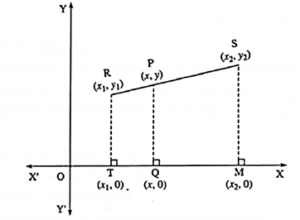
Assume R(x1, yl), S(x2, y2) and P(x, y). Draw seg RT,
seg PQ and seg SM perpendicular to X~axis.
∴ T(x1, 0); Q(x, 0) and M(x2, 0).
∴ TQ = x — x1 and QM = x2 — x …. (1)
seg RT|| seg PQ || seg SM.
∴ by the property of intercepts made by three parallel lines,
\(\frac{RP}{PS}=\frac{TQ}{QM}=\frac{m}{n}\)
Now TQ = x — x1 and QM = x2 — x …..[From(1)]
∴ \(\frac{x-x_1}{x_2-x}=\frac{m}{n}\)
∴ n(x—x1) = m(x2 - x)
∴ nx — nx1 = mx2—mx
∴ mx + nx = mx2 + nx1
∴ x(m + n) = mx2 + nx1
∴ x = \(\frac{mx_2+nx_1}{m+n}\)
Similarly, drawing perpendiculars from points R. P and S to Y-axis,
we get, y = \(\frac{my_2+ny_1}{m+n}\)
∴ coordinates of the point, which divides the line segment joining the points
R(x1, y1) and S(x2, y2) in the ratio m : n are given by
\((\frac{mx_2+nx_1}{m+n},\,\frac{my_2+ny_1}{m+n})\)
Example :
If A(3, 5), B(7, 9) and point Q divides seg AB in the ratio 2 : 3 then find co-ordinates of point Q.
Solution :
In the given example let (x1, y1)= (3, 5) and (x2, y2) = (7, 9) . m : n = 2 : 3
According to section formula,
x = \(\frac{mx_2+nx_1}{m+n}=\frac{2×7+3×3}{2+3}=\frac{23}{5}\)
y = \(\frac{my_2+ny_1}{m+n}=\frac{2×9+3×5}{2+3}=\frac{33}{5}\)
∴ Co-ordinates of Q are \((\frac{23}{5},\frac{33}{5})\)
Co-ordinates of the midpoint of a segment :
If A(x1, y1)and B(x2, y2) are two points and P (x, y) is the midpoint of seg AB, then m = n.
![]()
∴ values of x and y can be written as
| x = \(\frac{mx_2+nx_1}{m+n}\)
= \(\frac{mx_2+mx_1}{m+m}\) ….(m = n) = \(\frac{m(x_2+x_1)}{2m}\) = \(\frac{x_2+x_1}{2}\) |
y = \(\frac{my_2+ny_1}{m+n}\)
= \(\frac{my_2+my_1}{m+m}\) ….(m = n) = \(\frac{m(y_2+y_1)}{2m}\) = \(\frac{y_2+y_1}{2}\) |
∴ co-ordinates of midpoint P are \((\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})\)
This is called as midpoint formula.
Example :
Find the co-ordinates of point P if P is the midpoint of a line segment AB with A(-4, 2) and B(6, 2).
Solution :
In the given example, suppose
(-4, 2) = (x1, y1) ; (6, 2) = (x2, y2) and co-ordinates of P are (x, y)
∴ according to midpoint theorem,
x = \(\frac{x_2+x_1}{2}=\frac{6+(-4)}{2}=\frac{2}{2}\) = 1
y = \(\frac{y_2+y_1}{2}=\frac{2+2)}{2}=\frac{4}{2}\) = 2
∴ co-ordinates of midpoint P are (1, 2) .
Centroid formula :
- We know that, medians of a triangle are concurrent. The point of concurrence (centroid) divides the median in the ratio 2 : 1.
Suppose, in Δ ABC, A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices. Seg AM is a median and G(x, y) is the centroid.
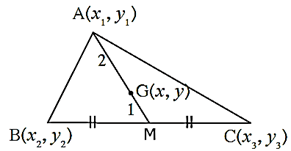
By definition of the median, M is the midpoint of seg BC.
Coordinates of M, by midpoint formula is \((\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})\)
G(x, y) is the centroid of Δ ABC
∴ AG : GM = 2 : 1
By section formula,
x = \(\frac{m(\frac{x_2+x_3}{2})+nx_1}{m+n}\)
= \(\frac{2(\frac{x_2+x_3}{2})+1(x_1)}{2+1}\)
= \(\frac{x_2+x_3+x_1}{3}=\frac{x_1+x_2+x_3}{3}\)
y = \(\frac{m(\frac{y_2+y_3}{2})+ny_1}{m+n}\)
= \(\frac{2(\frac{y_2+y_3}{2})+1(y_1)}{2+1}\)
= \(\frac{y_2+y_3+y_1}{3}=\frac{y_1+y_2+y_3}{3}\)
Thus, if (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle then the coordinates of the centroid are
\((\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})\)
This is called the centroid formula.
| Remember :
(i) Section formula : The coordinates of a point which divides the line segment joined by two distinct points (x1, yl) and (x2, y2) in the ratio m : n are \((\frac{mx_2+nx_1}{m+n},\,\frac{my_2+ny_1}{m+n})\) (ii) Midpoint formula : The coordinates of midpoint of a line segment joining two distinct points (x1, yl) and (x2, y2) are \((\frac{x_2+x_1}{2},\frac{y_2+y_1}{2})\) (iii) Centroid formula : If (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle then the coordinates of the centroid are \((\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})\) |
Example :
Find the co-ordinates of point P if P divides the line segment joining points A(-4, 6) and B(5, 10) in the ratio 3 : 1 externally.
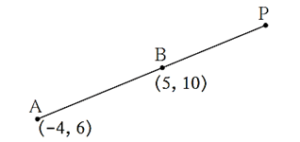
Solution :
\(\frac{AP}{PB}=\frac{3}{1}\) that is AP is larger than PB and A-B-P.
\(\frac{AP}{PB}=\frac{3}{1}\) that is AP = 3k, BP = k, then AB = 2k
∴ \(\frac{AB}{BP}=\frac{2}{1}\)
Now point B divides seg AP in the ratio 2 : 1.
Here m = 2, n = 1
Coordinates x = 5, y = 10, x1 = -4, y1 = 6,
Find out coordinates of Point P x2 and y2
By section formula,
| x = \(\frac{mx_2+nx_1}{m+n}\)
5 = \(\frac{2x_2+1(-4)}{2+1}=\frac{2x_2-4}{3}\) ∴ 5 × 3 = 2x2 -4 ∴ 2x2 = 15+4 = 19 ∴ x2 = \(\frac{19}{2}\) |
y = \(\frac{my_2+ny_1}{m+n}\)
10 = \(\frac{2y_2+1(6)}{2+1}=\frac{2y_2+6}{3}\) ∴ 10 × 3 = 2y2 + 6 ∴ 2y2 = 30 - 6 = 24 ∴ y2 = \(\frac{24}{2}\) = 12 |
∴ The coordinates of Point P are \((\frac{19}{2},12)\)
Slope of a line :
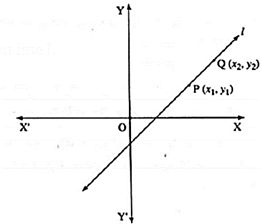
In the figure P(x1, y1) and Q(x2, y2) are any two points in XY-plane.
the ratio \(\frac{y_2-y_1}{x_2-x_1}\) is constant.
It is true for any two points on line l.
The ratio \(\frac{y_2-y_1}{x_2-x_1}\) is called the slope of the line l.
Usually slope is denoted by letter m.
∴ m = \(\frac{y_2-y_1}{x_2-x_1}\)
Slope of line – using ratio in trigonometry :
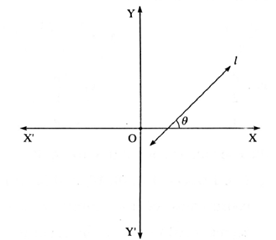
The tangent ratio of an angle made by the line with the positive direction of X-axis is called the slope of that line.
In the figure, line l makes an angle θ with the positive direction of X-axis.
slope of line l = m = tan θ.
Remember :
Slope of X-axis and any line parallel to X-axis is 0.
Slope of Y-axis and any line parallel to Y-axis cannot be determined.
Parallel lines have equal slopes.
When any two lines have same slope, these lines make equal angles with the
positive direction of X- axis. ∴ These two lines are parallel.
Example :
In the figure both line l and line t make angle θ with the positive direction of X- axis.
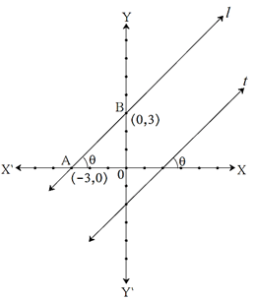
∴ line l || line t .......... (corresponding angle test)
Consider, point A(-3, 0) and point B(0, 3) on line l
Find the slope of line l.
Slope of line l = \(\frac{y_2-y_1}{x_2-x_1}=\frac{3-0}{0-(-3)}=\frac{3}{3}=1\)
slope, m = tan θ = 1, ∴ θ = 450
In the similar way, considering suitable points on the line t we can find the slope of
line t. From this, we can verify that parallel lines have equal slopes.
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-4-Geometric Construction – Online Notes
Next Chapter : Chapter-6-Co-ordinate Geometry – Online Notes
We reply to valid query.