Notes
|
Topics to be learn
|
Important formulae to find the surface areas and volumes :
(i) Cuboid : The cuboid consists of six surfaces. Each surface is rectangular.
Examples : Water Tank, Brick, matchbox, fish tank, etc.
If l, b, h denote the length, breadth and height of a cuboid, then
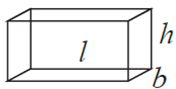
(1) lateral (vertical) surface area = 2(l + b)h
(2) total surface area = 2(lb + bh + hl)
(3) volume = lbh.
Question. The length, breadth and height of an oil can are 20 cm, 20 cm and 30 cm respectively as shown in the adjacent figure. How much oil will it contain ? (1 litre = 1000 cm3)
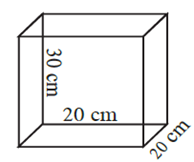
Given :
Oil tank shape = cuboid, length l = 20 cm, breadth b = 20 cm, height h = 30 cm
Oil contain in tank = Volume of the tank.
∴ Volume of the tank = l x b x h = 20 x 20 x 30 = 12000 cm3
∴ Oil contain in tank = \(\frac{12000}{1000}\)= 12 litre …….( 1 litre = 1000 cm3)
(ii) Cube : Cube is made up of six surfaces. Each surface is a square. All squares are equal.
Examples : Rubik's Cube, Ice cubes, die, etc.
If l is the length of each edge of a cube, then
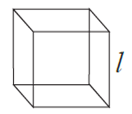
(1) lateral (vertical) surface area = 4 l2
(2) total surface area = 6 l2
(3) volume = l3
(iii) Cylinder : The cylinder is formed of three surfaces. The base surfaces are round in form. It also contains a curved surface.
Examples : Solid pipe, ball pens refills, road roller, coins, etc.
If r is the base radius and h is the height of a right circular cylinder, then
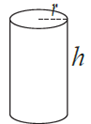
(1) area of the base surface = πr2
(2) curved surface area = 2πrh
(3) total surface area = 2πrh(r + h)
(4) volume = πr2h.
(iv) Right Circular Cone : A cone has two surfaces. Base surface is circular in shape. It also has curved surface.
Examples : Conical tent, ice-cream cone, Jokers’ conical hat, etc.
For a right circular cone of height h, slant height l and base radius r, we have,
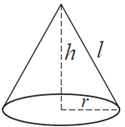
(1) area of the base = πr2
(2) l2 = r2 + h2
(3) curved surface area = πrl
(4) total surface area = πr(r + l)
(5) volume = \(\frac{1}{3}\)πr2h.
(v) Sphere : Sphere has only one surface which is entirely curved.
Examples : Football, marbles, soap bubbles, lead shots, etc.
If r is the radius of a sphere, then
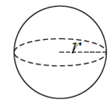
(1) surface area = 4πr2
(2) volume = \(\frac{4}{3}\)πr3
(vi) Hemisphere : Hemisphere has two surfaces. The base surface is circular in shape. It also has a curved surface.
Examples : Bowl, half broken coconut, etc.
If r is the radius of a hemisphere, then
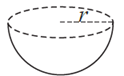
(1) area of the base = πr2
(2) curved surface area = 2πr2
(3) total surface area = 3 πr2
(4) volume = \(\frac{2}{3}\)πr3
Frustum of a cone :
When a cone is cut parallel to its base we get two figures; one is a cone and the other is a frustum.
Frustum has 3 surfaces. Two faces are circular and one is curved.
Volume and surface area of a frustum can be calculated by the formulae given below.
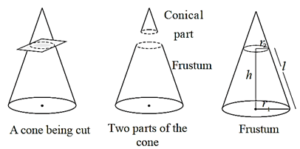
Examples : Bucket, Paper tea cup, etc.
If h is the height, r1, r2 are the radii of the bases ( r1 > r2) and the l is the slant height of the frustum of the cone. then
(1) l = \(\sqrt{h^2+(r_1-r_2)^2}\)
(2) curved surface area = πl(r1 + r2)
(3) total surface area = πl(r1 + r2) + πr12 + πr22
(4) volume = \(\frac{1}{3}\)πh(r12 + r22 + r1 × r2)
Example : A bucket is frustum shaped. Its height is 28 cm. Radii of circular faces are 12 cm and 15 cm. Find the capacity of the bucket. ( π = 22/7 )
Given : r1 = 15 cm, r2 = 12 cm, h = 28 cm
Capacity of the bucket = Volume of frustum
= \(\frac{1}{3}\)πh(r12 + r22 + r1 × r2)
= \(\frac{1}{3}×\frac{22}{7}\)× 28(152 + 122 + 15 × 12)
= \(\frac{88}{3}\)(225 + 144 + 180)
= \(\frac{88}{3}\)× 589 = 88 × 183 = 16104 cm3
1 litre = 1000 cm3
∴ Capacity of the bucket = \(\frac{16104}{1000}\) = 16.104 litre
Sector of a circle :
In the figure, the central angle divides the circular region in two parts.
The sector of a circle is the region bounded by two radii and the arc of the circle.
In the figure, arc ACB and arc ADB are the minor and the major arcs respectively.
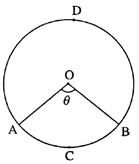
- Minor sector : The region bounded by the two radii and the minor arc is called minor sector.
- Major sector : The region bounded by the two radii and the major arc is the major sector.
Area of a sector :
In the figure, the region O-ACB is minor sector and the region O-ADB is the major sector.
Let m(arc ACB) = ∠ AOB = θ
Area of the sector = \(\frac{θ}{360}\)× πr2 ….(1)
Length of an arc
Circumference of the circle = 2πr or πd
Arc being the part of the circle, its length can be calculated.
Length of an arc (l) = \(\frac{θ}{360}\)× 2πr ….(2)
The relation between the length of the arc and the area of the sector is shown by the following formula :
∴ Area of a sector (A) = \(\frac{θ}{360}\)× πr2 = (\(\frac{θ}{360}\)× πr)\(\frac{r}{2}\)
= \(\frac{length\,of\,arc\,×\,radius}{2}\)
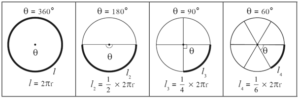
Similarly, \(\frac{A}{πr^2}=\frac{l}{2πr}=\frac{θ}{360}\)
Example : In figure side of square ABCD is 7 cm. With centre D and radius DA, sector D - AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region.
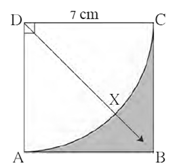
Area of a square = side2 = 72 = 49 cm2
Area of sector (D- AXC) = \(\frac{θ}{360}×πr^2\) = \(\frac{θ}{360}×\frac{22}{7}×7^2\) = 38.5 cm2
A (shaded region) = A (square) – A(D- AXC) = 49 cm2 – 38.5 cm2 = 10.5 cm2
Segment of a circle :
The region bounded by a chord and its corresponding arc is called the segment of the circle.
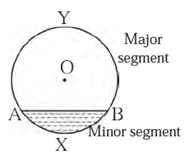
- Minor segment : If the corresponding arc is minor, then the segment is minor segment
- Major segment : If the corresponding arc is major, then the segment is major segment.
- Semicircular segment : A segment formed by a diameter of a circle is called a semicircular segment.
Area of a Segment
In the figure, the shaded region PXQ is the minor segment and region PYQ is the major segment of the circle.
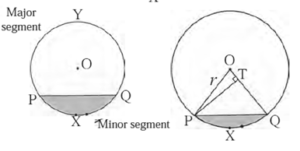
In the figure, if we draw radii OP and OQ, we also obtain sector O—PXQ.
Thus, Area of segment PXQ = [Area of sector O-PXQ] — [Area of triangle OPQ]
= \(\frac{θ}{360}×πr^2\) — [Area of triangle OPQ]
A(Δ OPQ) = \(\frac{1}{2}\)base × height = \(\frac{1}{2}\)r × r sin θ = \(\frac{1}{2}\)r2 sin θ
∴ Area of segment PXQ = \(\frac{θ}{360}×πr^2\) — \(\frac{1}{2}\)r2 sin θ
= \(r^2[\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
where r is the radius of the circle and θ is the angular measure of the arc contained by the sector.
(Note that, we have studied the sine ratios of acute angles only. So we can use the above formula when θ < 90°.)
Example : In the figure ∠ AOB = 30°, OA = 12 cm . Find the area of the segment. (π = 3.14)
A(segment AXB) = \(r^2[\frac{πθ}{360}-\frac{sin\,θ}{2}]\)
= \(12^2[\frac{3.14×30}{360}-\frac{sin\,30}{2}]\)
= 144\([\frac{3.14}{12}-\frac{1}{2×2}]\)
=\(\frac{144}{4}[\frac{3.14}{3}-1]\)
= 1.68 cm2
We reply to valid query.