Thermal Properties of Matter
Maharashtra Board-Class-11-Science-Physics-Chapter-7
Solutions
Question 1. Choose the correct option.
(i) Range of temperature in a clinical thermometer, which measures the temperature of human body, is
(A) 70 ºC to 100 ºC
(B) 34 ºC to 42 ºC
(C) 0 ºF to 100 ºF
(D) 34 ºF to 80 ºF
Answer :
(B) 34 ºC to 42 ºC
(ii) A glass bottle completely filled with water is kept in the freezer. Why does it crack?
(A) Bottle gets contracted
(B) Bottle is expanded
(C) Water expands on freezing
(D) Water contracts on freezing
Answer :
(D) Water contracts on freezing
(iii) If two temperatures differ by 25 °C on Celsius scale, the difference in temperature on Fahrenheit scale is
(A) 65°
(B) 45°
(C) 38°
(D) 25°
Answer :
(B) 45°
(iv) If α, β and γ are coefficients of linear, area l and volume expansion of a solid then
(A) α : β : γ = 1 : 3 : 2
(B) α : β : γ = 1 : 2 : 3
(C) α : β : γ = 2 : 3 : 1
(D) α : β : γ = 3 : 1 : 2
Answer :
(B) α : β : γ = 1 : 2 : 3
(v) Consider the following statements-
(I) The coefficient of linear expansion has dimension K—1
(II) The coefficient of volume expansion has dimension K—1
(A) I and II are both correct
(B) I is correct but II is wrong
(C) II is correct but I is wrong
(D) I and II are both wrong
Answer :
(A) I and II are both correct
(vi) Water falls from a height of 200 m. What is the difference in temperature between the water at the top and bottom of a water fall given that specific heat of water is 4200 J kg—1 °C—1?
(A) 0.96 °C
(B) 1.02 °C
(C) 0.46 °C
(D) 1.16 °C
Answer :
(C) 0.46 °C
Question 2. Answer the following questions.
(i) Clearly state the difference between heat and temperature?
Answer :
| Heat | Temperature |
| It is the energy in transfer from a body at higher temperature to a body at lower Temperature. | It is a quantitative measure of the degree of hotness or coolness of a body. |
| The SI unit of heat is the joule. | The SI unit of temperature is the kelvin. |
| The dimensions of heat are [L2M1'T-2K0]. | The dimension of temperature is [L0M0T0K1] |
(ii) How a thermometer is calibrated?
Answer :
- A thermometer is calibrated to measure a specific temperature on an empirical scale. A standard temperature interval is selected between two fixed points, the ice and steam points.
- The interval is divided into equal intervals, each called a degree of temperature,
- This procedure sets up an empirical scale for temperature.
(iii) What are different scales of temperature? What is the relation between them?
Answer :
There are three different scales of temperature namely the Celsius scale, Fahrenheit scale and absolute or thermodynamic scale. The units of temperature in these scales are the degree Celsius (°C), degree Fahrenheit (°F) and kelvin (K).
The relation between these three scales of temperature is
\(\frac{T_C}{100}=\frac{T_F-32}{180} =\frac{T_K-273.15}{100}\)
OR
\(\frac{T_C}{5}=\frac{T_F-32}{9} =\frac{T_K-273.15}{5}\)
(iv) What is absolute zero?
Answer :
The absolute zero of temperature, or the zero of the absolute or thermodynamic scale of temperature, is that temperature at which the energy of atoms and molecules of every material is minimum.
Since t (in °C) = T (in K) − 273.15, T = 0 K is
t = 0 K − 273.15 = − 273.15 °C
Also, in degree Fahrenheit,
t - 32 = \(\frac{9}{5}\)(T − 273.15) = \(\frac{9}{5}\)(0 K − 273.15) = − 491.67 °F
∴ t = − 491.67 + 32 = − 459.67 °F
(v) Derive the relation between three coefficients of thermal expansion.
Answer :
We have, β = 20: and γ = 3
∴ 3β = 6∝ ……..(1)
and 2γ = 6∝ ……..(2)
Combining Eqs. (1) and (2), we get,
6∝ = 3β = 2γ
Also, β = 2∝ and γ = 3∝. Hence, the relation between or, ∝, β and γ is
∝ = \(\frac{β}{2}\) = \(\frac{γ}{3}\)
Thus, the three coefficients are in the ratio
∝ : β : γ = 1 : 2 : 3
(vi) State applications of thermal expansion.
Answer :
Thermal expansion joints are small gaps between rails on a railway track, created due to thermal expansion during summer and friction during train travel.
- Thermal expansion joints are used in railway tracks, bridge spans, and factories to allow rails and pipelines to expand in summer due to friction and heat.
- These joints are also used in bullock carts, where an iron rim is heated to expand to a larger circumference.
- A bimetallic strip with different expansion coefficients is used as a circuit breaker.
- A tightly fitted metal lid on a glass jar can be loosened by inserting it in hot water, which expands the lid.
- Thermometers use mercury and alcohol to measure temperature changes by measuring the volume expansion of these substances.
These joints help ensure the safety and efficiency of various applications, such as transportation, manufacturing, and medical applications.
(vii) Why do we generally consider two specific heats for a gas?
Answer :
If Q is the amount of heat supplied to a substance of mass 111 and AT is the rise in
temperature of the substance, the specific heat of the substance is
s = \(\frac{Q}{mΔT}\)
When a gas is heated isothermally,
Q ≠ 0 but ΔT = 0.
∴ s = ∞
On the other hand, if a gas is compressed or allowed to expand adiabatically, i.e., no heat enters or leaves the gas, its temperature changes
but Q = 0 ∴ s = 0
Thus, it can be seen that the specific heat capacity of a gas can have any value from 0 to ∞, depending upon the conditions under which it is heated. Therefore, to fix the value of the specific heat capacity of a gas, in practice, either the volume or the pressure is kept constant. These two being the most important or principal conditions under which a gas is usually heated, we define two principal specific heat capacities for a gas, namely,
(i) specific heat capacity at constant volume (sv) and
(ii) specific heat capacity at constant pressure (Sp).
(viii) Are freezing point and melting point same with respect to change of state? Comment.
Answer :
At a given pressure, the transition between liquid and solid states occur at the same temperature, i.e., the fusion or freezing point is the same as the melting point.
(ix) Define
(i) Sublimation (ii) Triple point.
Answer :
Sublimation : Sublimation is the direct phase transition from solid to gaseous state without passing through the intermediate liquid state.
Triple point : Triple point is the point at which the fusion curve, vaporization curve and sublimation curve meet. It is the only combination of temperature and pressure at which all the three phases of matter are in equilibrium and can therefore exist simultaneously.
(x) Explain the term 'steady state'.
Answer :
Steady state : A thick metal rod of uniform cross section has one of its ends, ‘A’ maintained at a constant temperature by steam, see below Fig.

The opposite end ‘B’ is maintained at a constant lower temperature. The rod is covered with a thermal insulator (such as felt, slag wool or glass fibres — such materials are then called lagging) to prevent any heat loss from its longer surface. Thermometers are placed in holes drilled into the rod, with a small amount of mercury in each hole to ensure good thermal Contact between the rod and the bulb of a thermometer.
- Initially, as the end A is heated by steam, all the thermometers show a gradual rise in temperature.
- The section nearest to the steam end A always remains hottest.
- At this stage, as heat is being conducted, every section of the rod retains a part of this heat (which raises its temperature) and transmits the rest to the next section.
- After some time, the thermometer readings become stable, indicating that there is no further rise in the temperature of any section of the rod. Then, the rod is said to be in a thermal steady state.
(xi) Define coefficient of thermal conductivity. Derive its expression.
Answer :
Definition: The rate at which heat is conducted through two parallel surfaces of a block in the steady state divided by the area ofcross section and the temperature gradient is called the thermal conductivity or coefficient of thermal conduction of the material.
Let CG be a small section of length x of a lagged rod in a thermal steady state. The stable temperature at the end C is T1 and that at the end G is T2 < T1. The lagging ensures that there is no loss of heat to the surroundings through the cylindrical surface of the rod. Hence, all the heat passes through the rod in a direction normal to the cross sections C and G, (Fig.)
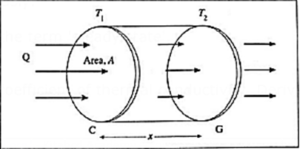
Since the rod is in a steady state, the quantity of heat entering per unit time through the end C of the section must be equal to that leaving the end G. It is found experimentally that the quantity of heat Q that flows from hot end to the cold end is directly proportional to
(i) the time t
(ii) the cross-sectional area A
(iii) the temperature difference between the two ends (T1 — T2) and is inversely proportional to
(iv) The perpendicular distance x between hot and cold ends That is,
Q ∝ A\((\frac{T_1-T_2}{x})\)t
Q = kA\((\frac{T_1-T_2}{x})\)t
where k is a constant of proportionality and is called the thermal conductivity. Thus, the thermal conductivity can be written as,
k = \(\frac{Qx}{A(T_1-T_2)t}\)
(xii) Give any four applications of thermal conductivity in everyday life.
Answer :
Applications of thermal conductivity:
(1) Thermal conductivity is a crucial factor in various applications, such as heating tubings in air-conditioning units and solar water heaters, and the insulation of water heaters. Copper is a good conductor of heat, making it ideal for transferring heat from the surrounding or sun to the fluid inside.
(2) Other poor conductors include sawdust, glass wool, and styrofoam, which trap air and are used in refrigerators and ice boxes.
(3) Clothes made from wool, felt, and synthetic sponge are comfortable in winter due to their ability to trap air within their texture, preventing heat loss to colder surroundings. Two bedsheets combined to cover the body help retain body heat better than a single bedsheet of double the thickness, as the layer of air between the sheets reduces thermal conduction. A blanket coupled with a bedsheet is a cheaper alternative to using two blankets.
(4) The handle of a cooking utensil is made of a bad conductor of heat, such as ebonite, to protect the hand from hot utensils.
(xiii) Explain the term thermal resistance. State its SI unit and dimensions.
Answer :
The opposition to the flow of heat through a body is called thermal resistance.
Definition: Thermal resistance is defined as the ratio of the temperature difference between the two parallel faces of a material to the rate at which heat is conducted through those surfaces. If Q is the quantity of heat conducted between two parallel surfaces of a slab in time t, the heat conduction rate is
\(\frac{Q}{t}\) = kA\((\frac{T_1-T_2}{x})\)
where k ≡ the thermal conductivity of the material,
A ≡ the cross-sectional area of each surface,
x ≡ the perpendicular distance between the two surfaces,
T1 − T2 ≡ the temperature difference between the two surfaces.
Then, the thermal resistance of the slab is,
RT = \(\frac{T_1-T_2}{Q/t}\) = \(\frac{x}{kA}\)
SI unit: The kelvin second per joule k-s/J
Dimensions = [RT] = [M-1L-2T3K1].
(xiv) How heat transfer occurs through radiation in absence of a medium?
Answer :
- Radiation is the process of heat transfer through electromagnetic waves without the need for any medium or heating.
- Thermal radiation, produced by body particles, is the radiation produced by a body above absolute zero of temperature.
- The spectrum of thermal radiation, which ranges from the far infrared to the extreme ultraviolet region, depends on the body's temperature.
- Infrared waves, with wavelengths ranging from 700 nm to 1 mm, are sensed as heat.
- When thermal radiations are incident on a body, they increase molecular motions, causing a rise in temperature.
- The transfer of heat by radiation is a two-fold process: the conversion of thermal energy into waves and the reconversion of waves into thermal energy by the body.
- Thermal radiation, as electromagnetic waves, has the same speed in free space as light, nearly 3 x 108 m/s, making it the most rapid mode of heat transfer.
(xv) State Newton’s law of cooling and explain how it can be experimentally verified.
Answer :
Newton's law of cooling: The time rate of fall of temperature of a body is directly
proportional to the excess temperature over the surroundings, provided the excess is small.
If T and T0 are the temperatures of a hot body and the surroundings, respectively, then by Newton's law of cooling, the time rate of fall of temperature of the body, i.e., the time rate of cooling, is
dT/dt ∝ (T − T0)
∴ dT/dt = C(T − T0)
where C is a proportionality constant in a particular case.
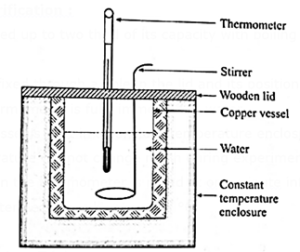
Experimental verification:
- A calorimeter is filled up to two third of its capacity with boiling water and is covered.
- A thermometer is fixed through a hole in the lid and its position is adjusted so that the bulb of the thermometer is fully immersed in water.
- The calorimeter vessel is kept in a constant temperature enclosure or just in open air since room temperature will not change much during experiment.
- The temperature on the thermometer is noted at one minute interval until the temperature of water decreases by about 25 °C.
- A graph of temperature T (along y-axis) is plotted against time t (along x-axis). This graph is called cooling curve (Fig).
- From this graph we can infer how the cooling of hot water depends on the difference of its temperature from that of its surroundings.
- We will also notice that initially the rate of cooling is higher and it decreases as the temperature of the water falls.
- A tangent is drawn to the curve at suitable points on the curve. The slope of each tangent (dT/dt) gives the rate of fall of temperature at that temperature.
- Taking (0,0) as the origin, if a graph of dT/dt is plotted against corresponding temperature difference (T-T0), the curve is a straight line as shown in Fig (a) and (b).
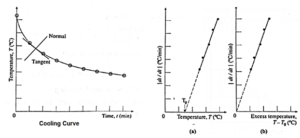
The above activity shows that a hot body loses heat to its surroundings in the form of heat radiation. The rate of loss of heat depends on the difference in the temperature of the body and its surroundings.
By either graph, we can conclude that dT/dt ∝ (T − T0)
This verifies Newton's law of cooling.
(xvi) What is thermal stress? Give an example of disadvantages of thermal stress in practical use?
Answer :
Thermal stress is the stress induced in a body due to change in temperature. Thermal stress is set up in a body when it is subjected to a change in temperature but is restricted from expanding or contracting.
Disadvantages of thermal stress :
- Temperature differences cause uneven expansion or contraction, leading to thermal stresses. For example, hot water in a glass vessel can cause cracking due to uneven expansion.
- Insufficient thermal expansion joints can cause railway tracks and bridge spans to distorted in summer, while electrical transmission lines may snap in cold weather due to contraction.
- Long metal pipelines with loops should be given proper space for expansion to avoid significant thermal stress, which can damage the pipelines and cause accidents. Proper slack is essential for preventing these issues.
(xvii) Which materials can be used as thermal insulators and why?
Answer :
Wood, cellulose, wool, hemp and foam are commonly used as thermal insulators.
An ideal thermal insulator should have the lowest thermal conductivity and highest heat resistance. Thus, less insulating material will be required.
Question 3. Solve the following problems.
(i) A glass flask has volume 1×10-4 m3. It is filled with a liquid at 30 ºC. If the temperature of the system is raised to 100 ºC, how much of the liquid will overflow. (Coefficient of volume expansion of glass is 1.2 × 10-5 (ºC)-1)
Answer :
Given : V = 1 x 10-4 m3, T1 = 30°C, T2 = 100°C,
γG = 1.2 x 10-5 °C-1, γL= 75 x 10-5 °C-1
Increase in the volume of the glass flask
= VγG(T2 − T1)
Increase in the volume of the liquid
= VγL(T2 − T1)
The volume of the liquid that will overflow
= VγL(T2 − T1) − VγG(T2 − T1)
= V(T − T1) (γL − γG)
= (1 x 10-4) (100 − 30) (75 − 1.2) x 10-5
= 70 x 73.8 x 10-9 = 5166 x 10-9
= 5.166 x 10-6 m3
(ii) Which will require more energy, heating a 2.0 kg block of lead by 30 K or heating a 4.0 kg block of copper by 5 K? (lead = 128 J kg-1 K-1, copper = 387 J kg-1 K-1)
Answer :
Given : mL = 2.0 kg, mc = 4.0 kg, SL =128 J Kg-1 K-1, SC =387 J Kg-1 k-1, TL =30 K, Tc = 5 K,
where T denotes the rise in temperature
QL = mLsL TL = 2 x 128 x 30 = 7680 J
QC = mCsC TC =4 x 387 x 5 =774O J
Copper block will require more energy.
(iii) Specific latent heat of vaporization of water is 2.26 × 106 J/kg. Calculate the energy needed to change 5.0 g of water into steam at 100 ºC.
Answer :
Given : Lv = 2.26 X 106 J/kg, m = 5.0 x 10-3 kg
Q = mLv
= (5.0 x 10-3) (2.26 x 106)
= 11.3 x 103 J
This is the required energy.
(iv) A metal sphere cools at the rate of 0.05 ºC/s when its temperature is 70 ºC and at the rate of 0.025 ºC/s when its temperature is 50 ºC. Determine (a) the temperature of the surroundings and (b) find the rate of cooling when the temperature of the metal sphere is 40 ºC.
Answer :
Given : \((\frac{dT}{dt})_1\) = 0.05 °C/s, T1 = 70 °C,
\((\frac{dT}{dt})_2\) = 0.025 °C/S, T2 = 50 °C, T3 = 40°C
(a) \(\frac{dT}{dt}\) = C(T − T0)
\((\frac{(dT/dt)_1}{(dT/dt)_2}\) = \(\frac{T_1-T_0}{T_2-T_0}\)
\(\frac{0.05}{0.025}=\frac{70-T_0}{50-T_0}\)
2 = \(\frac{70-T_0}{50-T_0}\)
100 – 2T0 = 70 – T0
T0 = 100 – 70 = 30°C
This is the temperature of the surroundings.
(b) \((\frac{(dT/dt)_3}{(dT/dt)_2}\) = \(\frac{T_3-T_0}{T_2-T_0}\)
= \(\frac{40-30}{50-30}=\frac{1}{2}\)
∴ \((\frac{dT}{dt})_3\) = \(\frac{1}{2}(\frac{dT}{dt})_2\) = \(\frac{1}{2}\) x 0.025 = 0.0125 °C
This is the rate of cooling when the temperature of the metal sphere is 40°C.
(v) The volume of a gas varied linearly with absolute temperature if its pressure is held constant. Suppose the gas does not liquefy even at very low temperatures, at what temperature the volume of the gas will be ideally zero?
Answer :
Given: p = constant
pV = nRT
for n moles of a gas. Here n = constant.
At constant pressure,
V → 0 as T → 0 K
The volume of the gas will be ideally zero at
0 K, i.e., — 273.15 °C.
(vi) In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 ºC. If maximum temperature in the region is 45 ºC and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10-5 K-1 for the material of the rail section?
Answer :
Given: T1 = 27°C, T2 = 45 °C, L1= 10 m, ∝ = 1.2 x 10-5 K-1 = 1.2 x 10-5 °C-1
Increase in the length of a rail section,
L2 − L1= ∝L1 (T2 − T1)
= (1.2 x 10-5) (10) (45 − 27)
= (1.2) (18) x 10-4
= 21.6 x 10-4 m
= 2.16 mm
This is the required gap between the consecutive rail sections.
(vii) A blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the wooden rim and the iron ring are 1.5 m and 1.47 m respectively at room temperature of 27 ºC. To what temperature the iron ring should be heated so that it can fit the rim of the wheel (∝iron = 1.2 × 10-5 K-1).
Answer :
Given : d1 = 1.47 m, d2 = 1.5 m, T1 = 27°C, ∝ = 1.2 x 10-5 K-1 =1.2 x 10-5 °C-1
Circumference = d
d2 – d1 = ∝ d1 (T2 – T1)
∴ T2 – T1 = \frac{d_2-d_1}{∝d_1}\) = \frac{1.5-1.47}{1.2×10^{-5}×1.47}\) = \(\frac{3000}{1.2×1.47}\) = 1701 °C
T2 = T1 + 1701 = 27 + 1701 = 1728°C
This is the required temperature.
(viii) In a random temperature scale X, water boils at 200 °X and freezes at 20 °X. Find the boiling point of a liquid in this scale if it boils at 62 °C.
Answer :
Rise of 100 °C corresponds to 200 °X - 20 °X = 180 °X
A rise of 62 °C would correspond to a rise of
\(\frac{180}{100}\) x (62 °X) = 1.8 x 62 = 111.6 °X on the scale X.
The boiling point of the liquid
= 20 °X + 111.6 °X = 131.6 °X
(ix) A gas at 900°C is cooled until both its pressure and volume are halved. Calculate its final temperature.
Answer :
Given: T1 = 900°C = (900 + 273.15) K = 173.15 K, p2 = p1/2 , V2 = V1/2
pV = nRt
p1V1 = nRT1 and p2V2 = nRT2
\(\frac{T_2}{T_1}=\frac{p_2V_2}{p_1V_1}\) = \((\frac{p_2}{p_1})(\frac{V_2}{V_1})\) = \((\frac{1}{2})(\frac{1}{2})\) = \(\frac{1}{4}\)
(x) An aluminium rod and iron rod show 1.5 m difference in their lengths when heated at all temperature. What are their lengths at 0 °C if coefficient of linear expansion for aluminium is 24.5 × 10—6/°C and for iron is 11.9 × 10—6 /°C
Answer :
Given : Difference in lengths = 1.5 m at all temperatures, am = 24.5 X 10—6/°C,
∝ = 11.9 x10—6/°C
LtI – L0I = ∝I L0I(T – T0)
LtAl – L0Al = ∝Al L0Al(T – T0)
LtI – L0I = LtAl – L0Al by the data
∴ ∝I L0I = ∝Al L0Al
∴ \(\frac{L_{0I}}{L_{0Al}}=\frac{∝_{Al}}{∝_I}\) = \(\frac{24.5×10^{-6}}{11.9×10^{-6}}\) = \(\frac{24.5}{11.9}\)
∴ L0l = \(\frac{24.5}{11.9}\)L0Al (1)
Now, L0I – L0Al = 1.5m (2)
∴ From (1) and (2), L0Al = \((\frac{24.5}{11.9}-1)L_{oAl}\) = 1.5
∴ L0Al = \(\frac{11.9×1.5}{24.5-11.9}=\frac{11.9×1.5}{12.6}\) = 1.4167m.
This is the length of the aluminium rod at 0 °C.
L0I = L0Al + 1.5 = 1.4167 + 1.5 = 2.9167 m
This is the length of the iron rod at 0 °C.
(xi) What is the specific heat of a metal if 50 cal of heat is needed to raise 6 kg of then metal from 20°C to 62 °C ?
Answer :
Given : Q = 50 cal, m = 6 kg, T1 = 20 °C, T2 = 62 °C
Q = ms(T2 - T1)
s = \(\frac{Q}{m(T_2-T_1)}\)
= \(\frac{50}{6(62-20)}\)
= 0.1984 cal/kg0C
This is the specific heat of the metal.
(xii) The rate of flow of heat through a copper rod with temperature difference 30 °C is 1500 cal/s. Find the thermal resistance of copper rod.
Answer :
Given : T1 − T2 = 30 °C, Q/t = 1500 cal/s
The thermal resistance of the copper rod,
RT = \(\frac{T_1-T_2}{Q/t}\) = \(\frac{30}{1500}\) = 0.02 \(\frac{°C}{cal/s}\)
(xiii) An electric kettle takes 20 minutes to heat a certain quantity of water from 0°C to its boiling point. It requires 90 minutes to turn all the water at 100°C into steam. Find the latent heat of vaporization. (Specific heat of water = 1cal/g°C)
Answer :
Given: t1 = 20 minutes, t2 = 90 minutes, s = 1 cal/g.°C
Q1 = ms (t2 – t1)
[Heating water from 0 °C to 100°C]
= m x 1(100°C - 0°C) = 100 m cal/g
Q2 = mLv
[Converting water at 100 °C into steam]
Now, Q2 = \(\frac{Q_1}{20min}×90min\)
As the source supplies the energy at a constant rate,
\(\frac{Q_2}{90min}= \frac{Q_1}{20min}\)
Q2 = \(\frac{9}{2}\)Q1 = 4.5 Q1
mLv = 4.5 x 100 m
Lv = 450 cal/g
This is the latent heat of the vaporization water.
(xiv) Find the temperature difference between two sides of a steel plate 4 cm thick, when heat is transmitted through the plate at the rate of 400 kcal per minute per square metre at steady state. Thermal conductivity of steel is 0.026 kcal/ms K.
Answer :
Given: \(\frac{Q}{At}\) = 400 kcal/minute.m2 = 400/60 kcal/s.m2 = 20/3 kcal/s-m2, x = 4 x 10-2 m, k = 0.026 kcal/m.s.K
k = \((\frac{Q}{At})(\frac{x}{T_1-T_2})\)
T1 – T2 = \((\frac{Q}{At})(\frac{x}{k})\) = \((\frac{20}{3})(\frac{4×10^{-2}}{0.026})\) = 10.26 K
This is the required temperature difference.
(xv) A metal sphere cools from 80 °C to 60 °C in 6 min. How much time with it take to cool from 60 °C to 40 °C if the room temperature is 30°C?
Answer :
Given : \((\frac{dT}{dt})_1=\frac{80-60}{6}=\frac{10}{3}\frac{°C}{min}\)
T1 = \(\frac{80+60}{2}\) = 70°C, T0 = 30°C
In part 2, T2 = \(\frac{60+40}{2}\) = 50 °C
and (dT)2 = 60°C − 40°C = 20°C
\(\frac{dT}{dt}\) = C (T1 – T0)
\(\frac{(dT/dt)_2}{(dT/dt)_1}\) = \(\frac{T_2-T_0}{T_1-T_0}\) = \(\frac{50-30}{70-30}\) = 1/2
∴ \((\frac{dT}{dt})_2\) = \((\frac{dT}{dt})_2 ×\frac{1}{2}\) = \(\frac{10}{3}×\frac{1}{2}\) = 5/3
∴ \(\frac{dT_2}{dt_2}=\frac{5}{3}\)
∴ dt2 = \(\frac{3}{5}\) x dT2 = \frac{3}{5}\) x 20
∴ dt2 = 12 minutes
This is the required time.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 6: Mechanical Properties of Solids – Online Solution
Next Chapter : Chapter 8: Sound – Online Solution
We reply to valid query.