Gravitation
Maharashtra Board-Class-11-Science-Physics-Chapter-5
Solutions
Question 1. Choose the correct option.
(i) The value of acceleration due to gravity is maximum at
(A) the equator of the Earth .
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
(C) the pole of the Earth.
(ii) The weight of a particle at the centre of the Earth is
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
(B) zero.
(iii) The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
(A) the centre of the Earth.
(iv) The binding energy of a satellite revolving around planet in a circular orbit is 3 × 109 J. Its kinetic energy is
(A) 6 × 109J
(B) -3 × 109J
(C) -6 × 10+9J
(D) 3 × 10+9J
(D) 3 × 10+9J
Question 2. Answer the following questions.
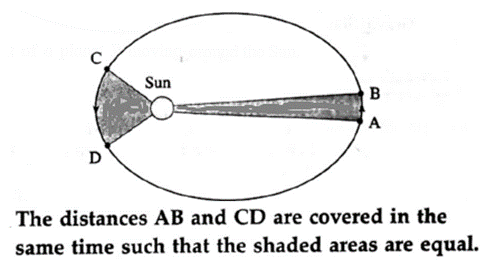
(i) State Kepler’s law equal of area.
Kepler’s Law of areas : The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
(ii) State Kepler’s law of period.
Kepler’s Law of periods : The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
(iii) What are the dimensions of the universal gravitational constant?
Dimensions of [G]= \(\frac{[F][r^2]}{[m_1m_2]}\) =\(\frac{[M^1L^1T^{-2}][M^0L^2T^0]}{[M^2L^0T^0]}\) = [M—1L3T—2]
(iv) Define binding energy of a satellite.
It is defined as the minimum energy that should be provided to the satellite to make it free from the gravitational influence of the Earth.
(v) What do you mean by geostationary satellite?
Geostationary satellite :
(vi) State Newton’s law of gravitation.
Newton's law of universal gravitation states that every particle in the universe attracts another with a force directly proportional to their masses, inversely proportional to the square of their distance, and acting along the joining line.
(vii) Define escape velocity of a satellite.
The escape velocity of a satellite is the minimum velocity with which it should be projected vertically upwards from the surface of the Earth so that it escapes from the Earth's gravitational field.
(viii) What is the variation in acceleration due to gravity with altitude?
The gravitational acceleration decreases with increasing altitude.
(ix) On which factors does the escape speed of a body from the surface of Earth depend?
The escape speed of a body ve = \(\sqrt{\frac{2GM}{R}}\) where G is the universal gravitational constant M is the mass of the Earth M and R is the radius of the Earth.
(x) As we go from one planet to another planet, how will the mass and weight of a body change?
The mass of a body at rest is invariant and does not change from one planet to another but the weight of the body will change.
(xi) What is periodic time of a geostationary satellite?
Periodic time of a geostationary satellite is 1 day i.e. 24 hrs.
(xii) State Newton’s law of gravitation and express it in vector form.
Newton's law of universal gravitation : Every particle of matter in the universe attracts every other particle with a force which is directly proportional to the product of their masses, inversely proportional to the square of the distance between them and acts along the line joining them. The force on particle 2 by particle 1 is \(\vec{F}_{21}\) . The force on particle 1 by particle 2 is \(\vec{F}_{12}\) \(\vec{F}_{12}\) = \(−\vec{F}_{21}\) . The forces and equal in magnitude and opposite in direction, form the action-reaction pair.

(xiii) What do you mean by gravitational constant? State its SI units.
Gravitational constant : According to Newton's law of universal gravitation, the force of attraction between two particles is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. F ∝ m1m2/r2 ∴ F = \(G\frac{m_1m_2}{r^2}\) The constant of proportionality G is called gravitational constant. It is a universal constant. The order of magnitude of G is 10−10 N.m2/Kg2 which makes the gravitational force a very weak force. SI unit of G : \(\frac{newton(metre)^2}{(kilogram)^2}\) or N.m2/Kg2 .
(xiv) Why is a minimum two stage rocket necessary for launching of a satellite?
Reason for minimum two-stage rocket using for launching of a satellite :
(xv) State the conditions for various possible orbits of a satellite depending upon the tangential speed of projection.
Conditions for various possible orbits of satellite depending upon the horizontal speed of projection : To put a satellite in an orbit around the Earth, it is raised to some altitude beyond the Earth's atmosphere and then projected horizontally with a velocity v. The path of the satellite depends on the value of v relative to the critical orbital velocity vc and the escape velocity ve. (i) v < vc : If tangential velocity of projection v is less than the critical velocity, the orbit of satellite is an ellipse with point of projection as apogee (farthest from the Earth) and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere, it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth. (ii) v = vc : The satellite enters into a circular orbit around the Earth and its motion is a uniform circular motion. (iii) vc < v < ve : The satellite moves in an elliptical orbit with the centre of the Earth at one focus. (iv) v > ve : The path of the satellite is no longer a closed curve and it escapes the Earth's gravitational influence. (v) v = ve : If horizontal speed of projection is equal to the escape speed at that height, the satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity. (vi) v > ve : (total energy positive), If horizontal velocity is greater than the escape velocity, the satellite escapes from gravitational influence of Earth transversing a hyperbolic path.
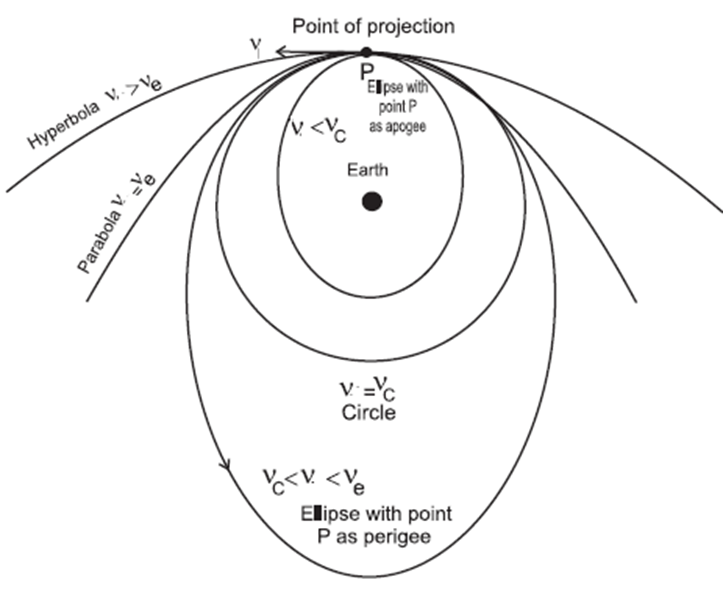
Question 3. Answer the following questions in detail.
(i) Derive an expression for critical velocity of a satellite.
Expression for critical velocity : Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius. If the satellite is moving in a circular orbit of radius (R+h) = r, its speed must be the magnitude of critical velocity vc. The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the Earth on the satellite. ∴ Centripetal force = Gravitational force ∴ \(\frac{mv_{c}^{2}}{r}\)=\(\frac{GmM}{r^2}\) ∴ vc2 = \(\frac{GM}{r}\) ∴ vc2 = \(\frac{GM}{R+h}\) ∴ vc = \(\sqrt{\frac{GM}{R+h}}\) This is the expression for critical velocity of a satellite.
(ii) State any four applications of a communication satellite.
Applications of a communication satellite : These are used for,
(iii) Show that acceleration due to gravity at height h above the Earth’s surface is gh = g\((\frac{R}{R+h})^2\)
The acceleration due to gravity on the Earth’s surface is given by, g = \(\frac{GM}{R^2}\) ….(1) Here M and R is the mass and radius of the Earth, g is the acceleration due to gravity at the Earth's surface and G the gravitational constant. Consider a body of mass m at an altitude h above the Earth’s surface. Then, its distance from the centre of the Earth is R + h. If gh is the acceleration due to gravity at the altitude h. Then, the weight of the body there is mgh and the gravitational force acting on it is Fg = \(\frac{GMm}{(R+h)^2}\) ∴ mgh = \(\frac{GMm}{(R+h)^2}\) ∴ gh = \(\frac{GM}{(R+h)^2}\) ….(1) Dividing Eq. (2) by Eq. (1), we get; ∴ gh = \(\frac{R^2}{(R+h)^2}\) = \(g(\frac{R}{(R+h)})^2\) ……(3) This is the expression for the gravitational acceleration at an altitude h.

(iv) Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Paths A and B (elliptical) : for v < vc Path C (circular) : for v = vc Path D (elliptical) : for vc < v < ve Path E (hyperbolic or parabolic) : for v ≥ ve
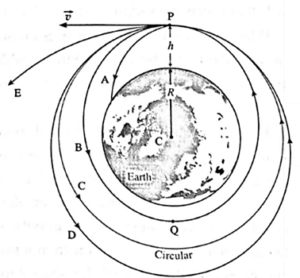
(v) Derive an expression for binding energy of a body at rest on the Earth’s surface.
Expression for Binding Energy of body rest on the Earth’s surface : Consider a body of mass m at rest on the Earth's surface, so that its kinetic energy (KE) is zero. Let M and R be the mass and radius of the Earth and G the gravitational constant. The gravitational potential at a point on the Earth’s surface = −GM/R Then, the gravitational potential energy (PE) of the body = \(-\frac{GM}{R}×m\) = \(-\frac{GMm}{R}\) Total energy of the body, E = PE + KE ∴ E = \(-\frac{GMm}{R}\) + 0 = \(-\frac{GMm}{R}\) The minus sign in the above expression shows that the body is bound to the Earth. If we provide the energy \(\frac{GMm}{R}\) to the body, its total energy will become zero, i.e., it will become just free from the gravitational influence of the Earth. Therefore, the binding energy of the body, BE = − E = \(\frac{GMm}{R}\)
(vi) Why do astronauts in an orbiting satellite have a feeling of weightlessness?
(vii) Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Graph of the variation of gravitational acceleration due to the depth and altitude from the Earth's surface : The expressions for the gravitational acceleration at a depth d and at an altitude h are, respectively, gd = \(g(1-\frac{d}{R})=g(\frac{r}{R})\) …. (1) and gh = \(g(\frac{R}{R+h})^2=g(\frac{R}{r})^2\) …. (2) where R is the radius of the Earth, and r is the distance from the centre of the Earth. In Eq. (1) r = R−d, while in Eq.(2) r = R+h. Using these expressions, the values of gd and gh for a few values of r are tabulated below. Using the values in the table we can plot the graph of g versus r.
r = R−d
gd
r = R+h
gh
0
0
R
g
R/4
g/4
2R
g/4
R/2
g/2
3R
g/9
R
g
4R
g/16
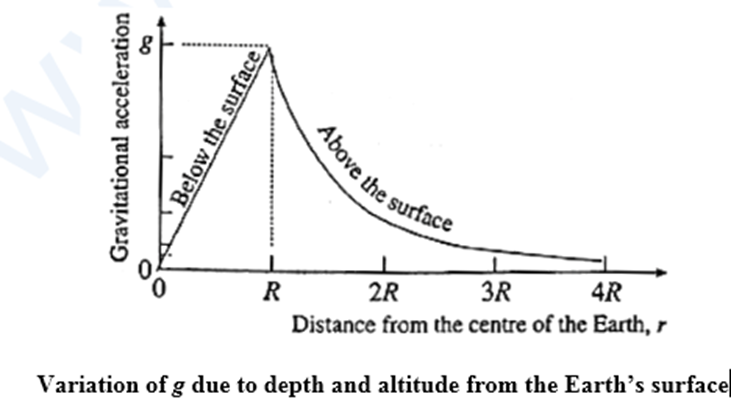
(viii) At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
The gravitational acceleration is maximum at the poles. The gravitational acceleration on the Earth's surface is g = GM/R2, where G, M and R are respectively the universal gravitational constant, mass of the Earth and radius of the Earth. The equatorial radius of the Earth is bigger than the polar radius because it is an oblate spheroid with an equatorial bulge. The gravitational acceleration also varies with latitude as a result of the planet's rotation around its axis. g on the surface of the Earth is minimum near the equator and largest at the poles as a result of the combined impacts of these two forces.
(ix) At which place on the Earth surface the gravitational acceleration minimum? Why?
The gravitational acceleration is minimum near the equator. The gravitational acceleration on the Earth's surface is g = GM/R2, where G, M and R are respectively the universal gravitational constant, mass of the Earth and radius of the Earth. The equatorial radius of the Earth is bigger than the polar radius because it is an oblate spheroid with an equatorial bulge. The gravitational acceleration also varies with latitude as a result of the planet's rotation around its axis. g on the surface of the Earth is minimum near the equator.
(x) Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Binding energy of a satellite : It is defined as the minimum energy that should be provided to the satellite to make it free from the gravitational influence of the Earth. Expression for binding energy of a satellite revolving around the Earth at a certain altitude : Consider a satellite performing uniform circular motion around the Earth. Let m = mass of the satellite, M = mass of the Earth, R = radius of the Earth, h = height of the satellite from the surface of the Earth, r ( = R + h) = radius of the orbit of the satellite, vc = critical orbital speed of the satellite. G = gravitational constant. The gravitational potential at a point at a distance r from the centre of the Earth = \(-\frac{GM}{r}\) [for r ≥ R ] ...(1) Gravitational potential energy (PE) of the satellite = \(-\frac{GM}{r}×m\) = \(-\frac{GMm}{r}\) ...(2) Kinetic energy (KE) of the satellite = \(\frac{1}{2}\)mvc2 And vc2 = GM/r ∴ KE = \(\frac{1}{2}\)m x \(\frac{GM}{r}\) = \(\frac{GMm}{2r}\) Total energy of the satellite, E = PE + KE ∴ E = \(-\frac{GMm}{r}\) + \(\frac{GMm}{2r}\) = \(-\frac{GMm}{2r}\) = \(-\frac{GMm}{2(R+h)}\) The minus sign in the expression for the total energy shows that the satellite is bound to the Earth. If we provide the energy \(\frac{GMm}{2r}\) to the satellite, its total energy will become zero, and hence, it will become free from the gravitational influence of the Earth. ∴ Binding energy of the satellite = −E = \(\frac{GMm}{2r}\) = \(\frac{GMm}{2(R+h)}\)
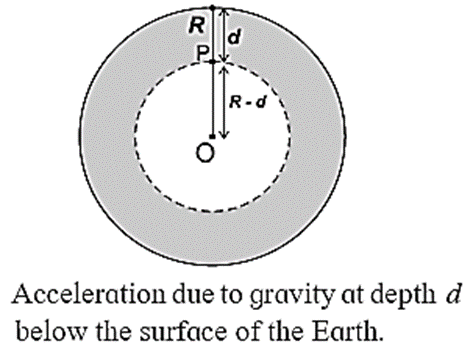
(xi) Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
The acceleration due to gravity on the Earth’s surface is given by, g = \(\frac{GM}{R^2}\) ….(1) Here M and R is the mass and radius of the Earth, g is the acceleration due to gravity at the Earth's surface and G the gravitational constant. Let the Earth be a solid sphere with uniform density. Density (ρ) = \(\frac{mass(M)}{volume(V)}\) = \(\frac{M}{\frac{4}{3}πR^3}\) ∴ M = \(\frac{4}{3}πR^3ρ\) Thus, Eq. (1) becomes g = \(\frac{G}{R^2}×\frac{4}{3}πR^3ρ\) = \(\frac{4}{3}πRρG\) ….(2) Consider a body of mass m at a depth d below the Earth's surface. Then, its distance from the Earth's centre is R − d. Let gd be the acceleration due to gravity at the depth d. Then, gd = \(\frac{GM'}{(R-d)^2}\) …..(3) Where M’ = volume of the inner sphere x density M’ = \(\frac{4}{3}π(R-d)^3ρ\) Thus, Eq. (3) becomes gd = \(\frac{\frac{4}{3}π(R-d)^3ρG}{(R-d)^2}\) ∴ gd = \(\frac{4}{3}π(R-d)ρG\) …..(4) Dividing Eq. (4) by Eq. (2), we get \(\frac{g_d}{g}\) = \(\frac{\frac{4}{3}π(R-d)ρG}{\frac{4}{3}πRρG}\) ∴ gd = \(g(1-\frac{d}{R})\) ….(5) This is the required expression. The expression shows that gd decreases with increasing depth. At the centre of the Earth, d = R, gd = 0
(xii) State Kepler’s three laws of planetary motion.
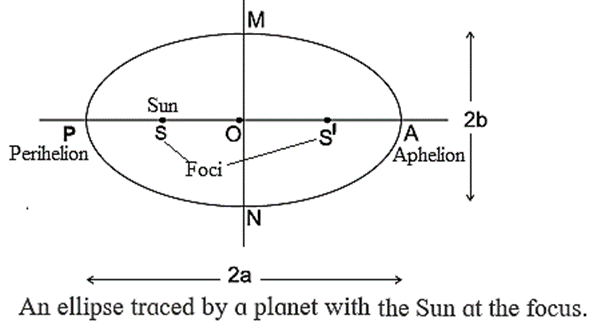
(1) Law of orbits : All planets move in elliptical orbits around the Sun with the Sun at one focus of the ellipse. The orbit of a planet around the Sun is shown in below Fig. (2) Kepler’s Law of areas : The line that joins a planet and the Sun sweeps equal areas in equal intervals of time. (3) Law of periods : The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet. If r is length of semi major axis then, this law states that T2 ∝ r3 Or T2/r3 = constant
(xiii) State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \((\frac{R-d}{R-2h})\) by assuming that the altitude is very small as compared to the radius of the Earth.
The acceleration due to gravity at a depth d gd = \(g(1-\frac{d}{R})\) …. (1) The acceleration due to gravity at an altitude h, gh = \(g(1-\frac{2h}{R})\) (as h << R) ….(2) Dividing Eq. (1) by Eq. (2), we get \(\frac{g_d}{g_h}=\frac{g(1-\frac{d}{R})}{g(1-\frac{2h}{R})}\) ∴ \(\frac{g_d}{g_h}=\frac{(\frac{R-d}{R})}{(\frac{R-2h}{R})}\) = \((\frac{R-d}{R-2h})\)
(xiv) What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Critical velocity : The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbit round the Earth is called the critical velocity or orbital velocity (vc) Expression for critical velocity : Consider a satellite of mass m revolving round the Earth at height h above its surface. Let M be the mass of the Earth and R be its radius. If the satellite is moving in a circular orbit of radius (R+h) = r, its speed must be the magnitude of critical velocity vc. The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the Earth on the satellite. ∴ Centripetal force = Gravitational force ∴ \(\frac{mv_{c}^{2}}{r}\)=\(\frac{GmM}{r^2}\) ∴ vc2 = \(\frac{GM}{r}\) ∴ vc2 = \(\frac{GM}{R+h}\) ∴ vc = \(\sqrt{\frac{GM}{R+h}}\) This is the expression for critical velocity for an orbital radius r = R + h. The expression shows that critical velocity vc ;

(xv) Define escape speed. Derive an expression for the escape speed of an object from the surface of the each.
Escape speed : The minimum speed with which a body should be projected from the surface of the Earth so that it escapes the Earth's gravitational field is called the escape speed of the body. Expression : Consider a body of mass m projected from the Earth's surface with escape speed ve. The kinetic and potential energies of the body, just after throwing it, KE = \(\frac{1}{2}\)mve2 PE = − GMm/R where G is the gravitational constant, M is the mass of the Earth and R is the radius of the Earth. Thus, the total energy of the object just after projection, = KE + PE = \(\frac{1}{2}\)mve2 − GMm/R …..(1) Under the Earth's gravitational pull, the speed of the body decreases with time. So, when the body reaches infinity, its speed becomes zero. Thus, kinetic and potential energies of the body at infinity, KE = 0 PE = − GMm/∞ = 0 Thus, the total energy of the body at infinity, = KE + PE = 0 ……(2) As the total energy is conserved, \(\frac{1}{2}\)mve2 − GMm/R = 0 ∴ \(\frac{1}{2}\)mve2 = GMm/R ∴ ve = \(\sqrt{\frac{2GM}{R}}\) This is the required expression.
(xvi) Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Launching of artificial satellite :
Question 4. Solve the following problems.
(i) At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km?
Given : gd = g − 0.1g = 0.9g, R = 6400 km ∴ \(\frac{g_d}{g}\) = 0.9 gd = \(g(1-\frac{d}{R})\) ∴ \(\frac{g_d}{g}=(1-\frac{d}{R})\) ∴ \(\frac{d}{R}=(1-\frac{g_d}{g})\) = 1 − 0.9 = 0.1 ∴ d = 0.1R = 0.1 x 6400 km = 640 km The required distance = 640 km
(ii) If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Given : M’ = 10% of M = 0.1M = 0.1 x 6 x 1024 kg = 6 x 1023 kg, R = 6400 km = 6.4 x 106 m, G = = 6.67 x 10-11 N-m2/kg2 The escape speed, ve = \(\sqrt{\frac{2GM'}{R}}=\sqrt{\frac{2×6.67×10^{-11}×6×10^{23}}{6.4×10^6}}\) = 3.538 x 103 m/s = 3.538 km/s
(iii) Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth. [Given:- G = 6.67 × 10-11 Nm2/kg2 R = 6400 km M = 6 × 1024 kg]
Given:- G = 6.67 × 10-11 Nm2/kg2 R = 6400 km M = 6 × 1024 kg, h = 3600 km, m = 2000 kg r = R + h = 6400 + 3600 = 10000 km = 107 m (1) The kinetic energy of the satellite = \(\frac{1}{2}mv_c^2=\frac{GmM}{2r}\) = \(\frac{6.67×10^{-11}×2000×6×10^{24}}{2×10^7}\) = 6.67 x 6 x 109 = 40.02 x 109 = 4.002 x 1010 J (2) The potential energy of the satellite = \(\frac{GmM}{2r}\) = −2KE = −2 x 4.002 x 1010 J = − 8.004 x 1010 J (3) The total energy of the satellite =PE + KE = −KE = − 4.002 x 1010 J (4) The binding energy of the satellite = − total energy = 4.002 x 1010 J
(iv) Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 104 km. find radius of orbit of satellite A.
Given: TA = 1 hour, TB = 8 hour, rB = 4 x 104 km To find: Radius of orbit of satellite A (rA) T2 = \((\frac{4π^2}{GM})r^3\) ∴ T2 ∝ r3 …\((\frac{4π^2}{GM})=\text{constant for planet}\) ∴\(\frac{T_A^2}{T_B^2}=\frac{r_A^3}{r_B^3}\) ∴ \(\frac{r_A}{r_B}\) = \((\frac{T_A^2}{T_B^2})^{1/3}=(\frac{1}{64})^{1/3}=\frac{1}{4}\) ∴ The radius of orbit of satellite A, rA = \(\frac{r_B}{4}=\frac{4×10^4}{4}\) = 1 × 104 km
(v) Find the gravitational force between the Sun and the Earth.
Given : Mass of the Sun = 1.99 × 1030 kg, Mass of the Earth = 5.98 × 1024 kg, The average distance between the Earth and the Sun = 1.5 × 1011 m.
Given : MS = 1.99 x 1030 kg, ME = 5.98 x 1024 kg, r = 1.5 x 1011 m, G = 6.67 x 10-11 N-m2/kg2 The magnitude of the gravitational force between the Sun and the Earth, F = \(\frac{GM_SM_E}{r^2}=\frac{6.67×10^{11}×1.99×10^{30}×5.98×10^{24}}{(1.5×10^{11})^2}\) = 35.28 x 1021 = 3.528 x 1022 N
(vi) Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 ×1024 kg, R = 6400 km).
Given :G = 6.67 x 10-11 N-m2/kg2, M = 5.98 x 1024 kg, R = 6400 km, h = 300 km r =R + h = 6400 + 300 = 6700 km = 6.7 x 106 m gh = \(\frac{GM}{r^2}=\frac{6.67×10^{11}×5.98×10^{24}}{(6.7×10^6)^2}\) = 8.885 m/s2 This is the required acceleration due to gravity.
(vii) Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. ME = 5.98 ×1024 kg, R = 6.4×106 m.
Given : G = 6.67 x 10-11 N-m2/kg2, M = 5.98 x 1024 kg, R = 6.4 x 106 m, h = 1000 km = 1 x 106 m ∴ r =R + h = 6.4 x 106 + 1 x 106 = 7.4 x 106 m vc = \(\sqrt{\frac{GM}{r}}=\sqrt{\frac{6.67×10^{11}×5.98×10^{24}}{7.4×10^6}}=\sqrt{53.90×10^6}\) = 7.342 x 103 m/s 7.342 x 103 m/s is the required speed.
(viii) Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4×103 km and its mass is 6.4 × 1023 kg.
Given : G = 6.67 x 10-11 N-m2/kg2, M = 6.4 x 1023 kg, R = 3.4 x 103 km = 3.4 x 106 m On the surface of Mars g = \(\frac{GM}{R^2}=\frac{6.67×10^{-11}×6.4×10^{23}}{(3.4×10^6)^2}\) =\(\frac{6.67×6.4}{(3.4)^2}\) = 3.693 m/s2
(ix) A planet has mass 6.4 ×1024 kg and radius 3.4 × 106 m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Given : G = 6.67 x 10-11 N-m2/kg2, M = 6.4 x 1024 kg, m = 800 kg, R = 3.4 x 106 m Energy required to remove on object of mass ‘m’ from the surface of the planet to infinity = Binding Energy B.E. = \(\frac{GmM}{R}=\frac{6.67×10^{-11}×800×6.4×10^{24}}{(3.4×10^6)^2}\) = 1.004 x 1011 J 1.004 x 1011 J is the required energy
(x) Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6×1024 kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s2
Given : M = 6 x 1024 kg, R = 6400 km = 6.4 x 106 m, g = 9.8 m/s2 g = \(\frac{GM}{R^2}\) ∴ The universal gravitational \)constant, G = \(\frac{gR^2}{M}=\frac{9.8(6.4×10^6)^2}{6×10^{24}}\) = 6.69 x 10-11 N-m2/kg2
(xi) A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 7 times the mass of the Earth and radius twice that of the Earth’s radius.
Given : WE = 5.6 kg wt, MP = ME/7, RP = 2RE Weight W = mg = \(\frac{GmM}{R^2}\) ∴ WP = \(\frac{GmM_P}{R_P^2}\) and WE = (\frac{GmM_E}{R_E^2}\) ∴ \(\frac{W_P}{W_E}\) = \((\frac{M_P}{M_E})(\frac{R_E^2}{R_P^2})\) = \((\frac{1}{7})(\frac{1}{2})^2=\frac{1}{28}\) ∴ WP = \(\frac{W_E}{28}=\frac{5.6}{28}\) = 0.2 kg wt The weight of the body on the planet = 0.2 kg wt
(xii) What is the gravitational potential due to the Earth at a point which is at a height of 2RE above the surface of the Earth, Mass of the Earth is 6 × 1024 kg, radius of the Earth = 6400 km and G = 6.67 × 10-11 Nm2 kg-2.
Given : RE = 6400 km, h = 2RE, M = 6 x 1024 kg, G = 6.67 × 10-11 Nm2 kg-2 r = RE + h = 3RE = 3 x 6400 km = 3 x 6.4 x 106 m The gravitational potential at the given point = \(-\frac{GM}{r}\) = \(-\frac{6.67×10^{-11}×6.4×10^{24}}{3×6.4×10^6}\)\) = − 2.084 x 107 J/kg
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 4: Laws of Motion – Online Solutions
Next Chapter : Chapter 6: Mechanical Properties of Solids – Online Solutions
We reply to valid query.