Notes Part-1
|
Topics to be Learn : Part-1
|
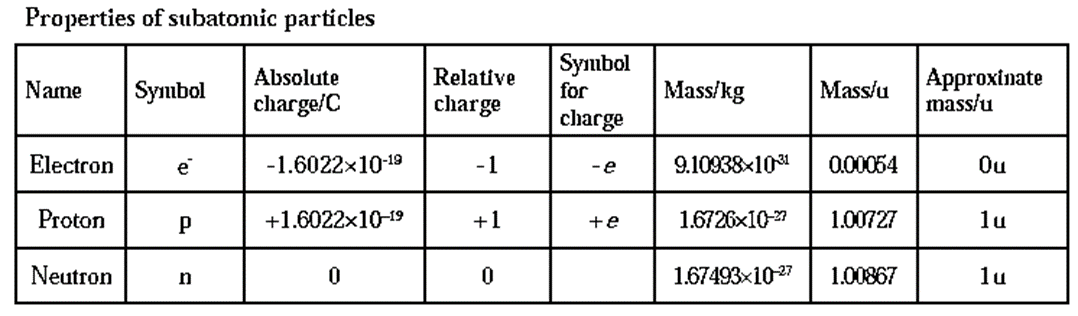
Subatomic particles :
- Three important subatomic particles : Proton, electron and neutron
- Proton and neutron are present in the atomic nucleus and together are called nucleons.
- Electrons are present in the extra nuclear part of an atom.
- Electron discovered by J. J. Thomson
- Proton discovered by Ernest Rutherford
- Neutron discovered by James Chadwick
With the detailed studies of a nucleus of an atom, following subatomic particles have been discovered :
- (i) Electrons (ii) Protons (iii) Neutrons (iv) Mesons (v) Positrons (vi) Neutrinos (vii) Antiprotons (viii) Quarks (ix) Pions (x) Gluons.
The properties of a neutron are :
- It is slightly heavier than proton and has mass, 1.67493 x 10-27 g.
- It does not carry any electric charge hence it is electrically neutral.
- It imparts the stability to the nucleus of an atom.
- Except hydrogen atom (\(_{1}^{1}\text{H}\)), all atoms have neutrons in their nucleus along with protons.
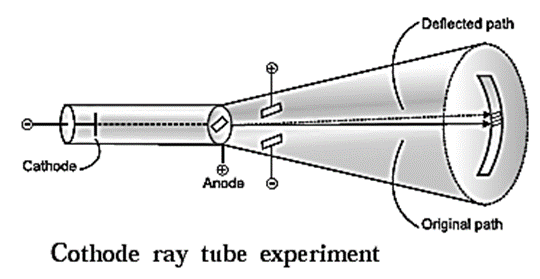
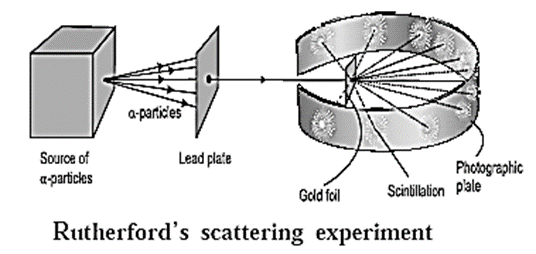
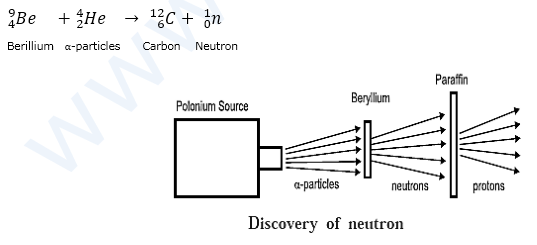
Discovery of electron : In the year 1897, J. J. Thomson investigated the cathode rays and found that the cathode rays are a stream of very small, negatively charged particles which are 1837 times lighter than a hydrogen atom and are present in all atoms. Later these particles were named as electrons. Discovery of proton : In the year 1911, Ernest Rutherford found in the experiment of scattering of α -particles by thin gold foil (see Fig) that a few α-particles bounce back. From this he inferred the presence of massive and positively charged nucleus inside the atom. Later in 1919 Rutherford found that α-particles striking on nitrogen nuclei produced protons ( ) by nuclear transmutation of nitrogen into oxygen. \(_{\,\,7}^{14}\textrm{N} + _{3}^{4}\textrm{α}→_{\,\,8}^{17}\textrm{O} + _{1}^{1}\textrm{H}\) (proton) Further it was observed that other elements also on transmutation emit hydrogen atoms. On this basis Rutherford concluded that the hydrogen nucleus must be present inside the nuclei of atoms of all the elements. Therefore hydrogen nucleus was named as proton and represented as \(_{1}^{1}\text{H}\) carrying unit positive charge. Discovery of neutron : Ernest Rutherford in 1920 predicted the presence of neutrons to account for disparity in atomic number and atomic mass of an elements. James Chadwick observed the emission of high velocity unidentified neutral radiations when beryllium was bombarded by on-particles. These unidentified neutral radiations on striking paraffin emitted protons. He found that the unidentified particles did not have an electric charge but has a mass almost the same as that of a proton. This neutral particle was named as neutron and denoted by \(_{0}^{1}\text{n}\) . The nuclear transmutation reaction is,
Atomic number and atomic mass number :
Atomic number : The number of protons present in the nucleus of an atom of an element is called atomic number and denoted by Z.
Mass number : The total number of protons and neutrons that is total number of nucleons present in the nucleus of an atom is called atomic mass number and denoted by A.
Mass number (A) =Number of protons (Z) + Number of neutrons (N) ,
A = Z + N
Nuclide : The atom or nucleus having unique composition as specified by\(_{Z}^{A}\text{X}\) . is called nuclide. For example \(_{\,\,6}^{12}\text{C}\) ..
- The composition of any atom is represented by element symbol (X) with the atomic mass number (A) as superscript on left and atomic number (Z) as subscript on left :
Isotopes, isobars and isotones :
Isotopes : The atomic species of an element possessing same atomic number but different mass numbers are called isotopes.
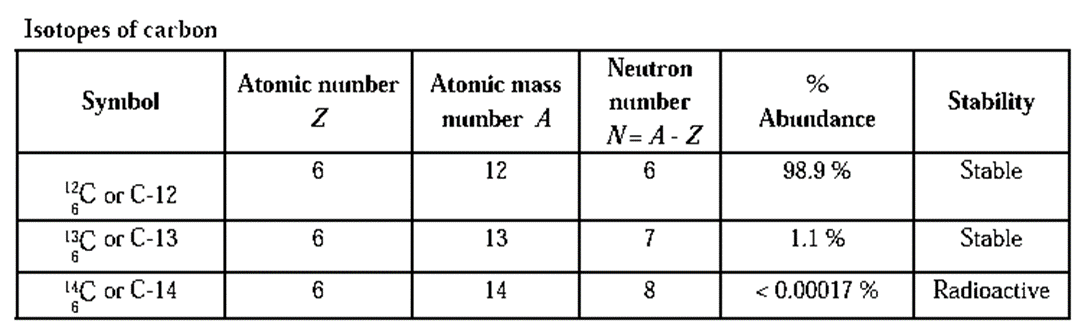
The characteristics of isotopes are as follows :
Isobars : The atoms of different elements which have the same mass number but different atomic numbers are called isobars.
The characteristics of isobars are as follows
Isotones : The atoms of different elements having same number of neutrons in their nuclei are called isotones.
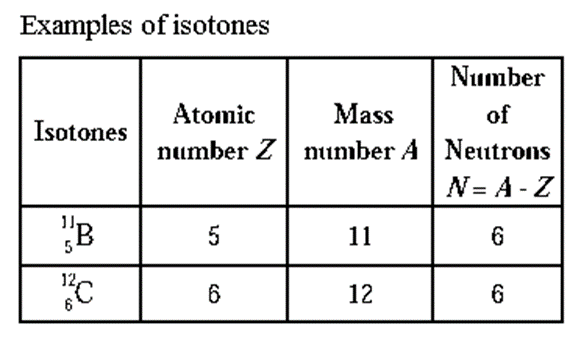
Drawbacks of Rutherford atomic model :
Rutherford’s atomic model has following drawbacks :
- According to the classical electromagnetic theory, a revolving charged particle like electron should emit radiation and lose energy. Due to this, electron should come closer to the nucleus by following a spiral path and finally fall into the nucleus, giving unstable atom. But in reality atoms are stable.
- The orbital motion is an accelerated motion accompanied by continuous change in the velocity of electron due to changing direction.
- Orbital motion of an electron dos not explain the change in energy and hence atomic spectrum.
- The electron would follow a spiral path and fall into the nucleus.
- This model does not explain the distribution of electrons around the nucleus and their energies.
The drawbacks of the Rutherford model were overcome in the Bohr atomic model.
Developments leading to the Bohr’s atomic model :
Results obtained from the studies of interactions of radiation with matter required to be correlated to atomic structure.
Niels Bohr utilized these results and on the basis of following aspects got over the drawbacks of Rutherford’s atomic model :
- Wave particle duality of electromagnetic radiation.
- Line emission spectra of hydrogen.
Wave particle duality of electromagnetic radiation :
A dilemma was posed by electromagnetic radiation in the world of science.
- Phenomenon such as diffraction and interference of light could be explained on the basis of wave nature of electromagnetic radiation.
- Black—body radiation or photoelectric effect could not be explained by wave nature but could be explained by particle nature of electromagnetic radiation.
- Thus when light interacts with matter it behaves as a stream of particles called photons while when light propogates, it behaves as an electromagnetic wave.
Characteristics of electromagnetic wave : Above Figure shows a schematic representation of an electromagnetic wave. Various parameters used to describe the different types of electromagnetic radiation are wavelength, frequency, wavenumber, amplitude, and velocity.
Particle nature of electromagnetic radiation :
According to Max Planck the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation is called ‘quantum’.
The energy (E) of one quantum of radiation is proportional to its frequency (ν) and given by
E = h ν = hc/λ
The proportionality constant ‘h’ is called Plank’s Constant (6.626 × 10−34 Js).
Photoelectric effect :
In the year 1905, Albert Einstein explained the photoelectric effect using Plank’s quantum theory.
When a beam of light of sufficient energy is allowed to strike a surface of a metal, electrons are ejected. This phenomenon is known as photoelectric effect and the ejected electrons are called photo electrons.
The features of photo-electric effect are as follows :
- The incident light must have certain minimum frequency (or energy) required to eject electrons from a particular metal. This frequency is called threshold frequency (νo) and the energy associated with this frequency is called threshold energy.
- The energy of emitted photoelectrons is given by Einstein's photoelectric equation, hv = hνo + ½ mv2 , where m and v are mass and velocity of photo-electrons respectively.
- Einstein considered electromagnetic radiation as a stream of photons of energy hν. A photon has zero rest mass. (Planck's constant, h = 6.626 × 10−34 Js)
Line emission spectrum of hydrogen : Emission spectrum : When a substance is irradiated with light it absorbs energy. Atoms, molecules or ions, which have absorbed radiation are said to be ‘excited’. When an excited species gives away the absorbed energy in the form of radiation, the process is called emission of radiation. The recorded spectrum of this emitted radiation is called ‘emission spectrum’. When an electric discharge is passed through gaseous hydrogen, it emits radiation. The hydrogen emission spectrum is not continuous but comprised of a series of lines corresponding to different frequencies and wavelengths. A relation for wave number \(\bar{v}=\frac{1}{λ}\) was given by Ritz combination principle as follows, \(\bar{v}=R_H(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}})\) where RH is Rydberg constant while n1 and n2 are orbit numbers. (RH = 1.09677 x 107 m−1 or 109677 cm−1) In 1885, Balmer gave relation for wavenumbers of spectral lines in visible region as, \(\bar{v}=109677(\frac{1}{2^2}-\frac{1}{n_{2}^{2}})\)
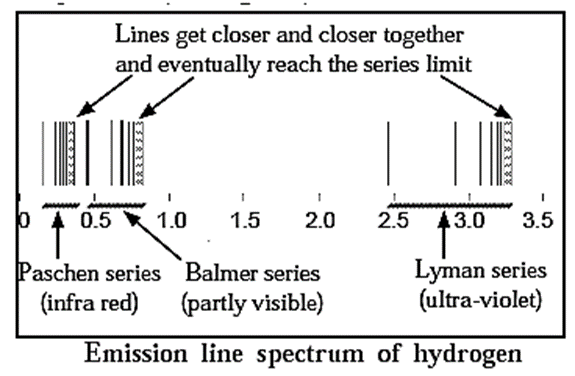
| Know This :
Fluorescent tube, sodium vapor lamp, neon sign, halogen lamp are all examples of atomic emission. |
Bohr’s model for hydrogen atom :
Niels Bohr (1913) put forth his postulates about the atomic model for hydrogen.
He used the quantum theory, wave particle duality of electromagnetic radiation and the emission line spectra of hydrogen.
Postulates of Bohr atomic theory Bohr’s model of hydrogen atom is based on the following postulates. (i) The electron in the hydrogen atom can move around the nucleus in certain permitted circular orbits arranged concentrically in increasing order of energy. (ii) The energy of an electron in the orbit does not change with time. Hence orbits are called stationary orbits. On absorption of required energy electron moves from lower orbit to higher orbit. The transition from higher energy orbit to lower energy orbit is accompanied by emission of energy in the form of electromagnetic radiation. (iii) The frequency ν of radiation absorbed or emitted on transition between two stationary orbits differing by energy ΔE is given by, ν = ΔE/h = E2 − E1 where E1 and E2 are the energies of the lower and higher energy states respectively. Above equation represents Bohr’s frequency rule. (iv) An electron can occupy only those orbits in which its angular momentum is integral (n) multiple of h/2π Angular momentum = \(\frac{nh}{2π}\)
| Angular Momentum :
Angular momentum is a product of moment of inertia (I) and angular velocity (ω) omega Angular momentum = I × ω ; but I = m r2 and ω = v/r ∴ Angular momentum = mr2 × v/r = mvr |
Results of Bohr’s theory :
Bohr radius : The radius of the first stationary orbit in hydrogen atom is called Bohr radius which is 52.9 pm.
Bohr’s theory is used to obtain the energies of stationary orbits in hydrogen atom.
(a) The stationary states or orbits for electron are represented by principal quantum numbers, n = 1, 2, 3, .... .. .
(b) The radii of stationary orbits are given by, rn = n2a0, where a0 = 52.9 pm.
(c) The energy of a stationary state (orbit) is given by
En = −RH x (1/n2), where RH is Rydberg constant.
RH = 2.18 x 10−18J
(d) Bohr’s theory can be applied to hydrogen like atomic species with one electron.
For example, H, He+, Li2+, etc.
The energy of a stationary state is given by,
En = −2.18 x 10−18 \(\frac{Z^2}{n^2}\) ...where Z is the atomic number of species.
The radius of nth orbit is given by
rn = \(\frac{52.9×n^2}{Z}\) pm … where Z is the atomic number.
From the above expression it can be seen that the energy decreases (becomes more negative) and radius becomes smaller as the value of Z increases.
(e) Velocities of electrons can also be calculated from the Bohr theory. Qualitatively it is found that the magnitude of velocity of an electron increases with increase of Z and decreases with increase in the principal quantum number n.
| Know This :
What does the negative sign of electron energy convey ?
|
Explanation of the line spectrum of hydrogen using Bohr theory :
Various spectral series present in hydrogen spectrum :
Each spectral line arises due to the transition of an electron from higher energy level (n2) to lower energy level (n1). The wave number, 5 of the spectral line is given by,
\(\bar{v}=R(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}})\) …. where R is Rydberg’s constant.
From the given excited higher energy level, the electron can jump to various lower energy levels. Depending upon the lower energy levels to which the electron jumps, there arise various series.
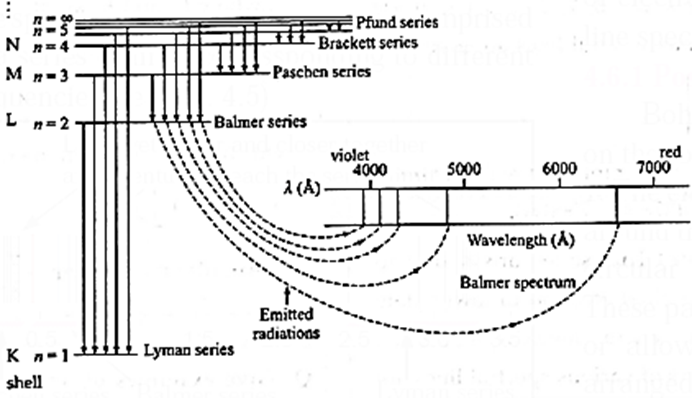
Series of emission spectral lines for hydrogen : Lyman series : The Lyman series is the result of moving of electron excited to higher orbits of n2= ni = 2, 3, 4,.....etc. to lower orbits of n1 = nf = 1; (first energy level of K shell) These spectral lines correspond to the highest energy, hence have short wavelength in ultra-violet region (920 — 1200 Å). Balmer series : Balmer series results from electron from n2 = ni = 3, 4,........ to the lower orbit of n1= nf = 2, so on and so forth. These spectral lines correspond to comparatively lower energy, hence have intermediate wavelengths in the visible region (4000 - 6500 Å). Paschen series : The energy of emitted radiations in this series is low and these lines appear in the infrared region of long wavelengths (9500 - 18750 Å). Bracket series : These lines appear in far infrared region of long wavelengths (19450 - 40500 Å). Pfund series : These lines appear in far infrared region of quite long wavelength (37800 — 7500 Å). The electronic transitions giving rise to different emission line series of atomic hydrogen are shown in Fig
Series
n1
n2
Spectral region
Lyman
1
2,3…
Ultraviolet
Balmer
2
3,4…
Visible
Paschen
3
4,5….
Infrared
Bracket
4
5,6…
Infrared
Pfund
5
6,7…
Infrared
Limitations of Bohr model
- Bohr’s atomic model failed to account for finer details of the hydrogen atom spectrum observed in sophisticated spectroscope experiments.
- Bohr model was unable to explain the spectrum of atoms other than hydrogen.
- Bohr theory could not explain the splitting of spectral lines in the presence of a magnetic field (Zeeman effect) or electric field (Stark effect).
- Bohr theory failed to explain the ability of atoms to form molecules by chemical bonds.
It was, therefore, thought that a better theory was needed to explain salient features of atomic structure.
| Know This :
The Bohr’s theory is applicable to hydrogen atom and hydrogen-like species which contain only one extranuclear electron. |
Reasons for failure of the Bohr model :
With the limitations of Bohr model for hydrogen atom becoming transparent, attempts were made to develop a better and general model for atom. This was possible because two important developments took place after the Bohr model was postulated.
These development were :
- de Broglie’s proposal of dual behaviour of matter
- Heisenberg uncertainty principle.
de Broglie’s equation :
- de Broglie suggested that all material objects exhibit dual nature i.e., particle nature and wave nature.
- As a particle, an object has mass m, velocity v and kinetic energy ½ mv2.
- As a wave, a particle has wavelength λ and frequency v.
- Dual nature is more prominent in case of objects having extremely small masses like electrons.
- Louis de Broglie interrelated these two properties by an equation, λ = h/mv, where h is Planck's constant.
- The quantity mv represents the momentum p of a particle, hence λ = h/p.
- This de Broglie’s equation has been extensively used to explain the dual properties of an electron.
Statement of Heisenberg's uncertainty principle :
This principle states that it is not possible to determine simultaneously the position and momentum of a moving microscopic particle like electron with absolute certainty.
This uncertainty arises due to dual nature of a particle like electron. If Δx is the uncertainty in the measurement of its position and Δp is the uncertainty in the measurement of momentum then by Heisenberg’s principle,
Δx x Δp ≥ h/4π
Since Δp = m x Δv
∴ Δx x m x Δv = h/4π
where Δv is the uncertainty in the measurement of velocity of a particle of mass m.
We reply to valid query.