Sound
Maharashtra Board-Class-11-Science-Physics-Chapter-8
Solutions
(1) Choose the correct alternatives
(i) A sound carried by air from a sitar to a listener is a wave of following type.
(A) Longitudinal stationary
(B)Transverse progressive
(C) Transverse stationary
(D) Longitudinal progressive
(D) Longitudinal progressive
(ii) When sound waves travel from air to water, which of these remains constant?
(A) Velocity
(B) Frequency
(C) Wavelength
(D) All of above
(B) Frequency
(iii) The Laplace’s correction in the expression for velocity of sound given by Newton is needed because sound waves
(A) are longitudinal
(B) propagate isothermally
(C) propagate adiabatically
(D) are of long wavelength
(C) propagate adiabatically
(iv) Speed of sound is maximum in
(A) air
(B) water
(C) vacuum
(D) solid
(D) solid
(v) The walls of the hall built for music concerns should
(A) amplify sound
(B) reflect sound
(C) transmit sound
(D) absorb sound
(D) absorb sound
(2) Answer briefly.
(i) Wave motion is doubly periodic. Explain.
- When a wave travels through a medium, at any point of the medium, the form of the wave repeats after equal intervals of time. Thus, a wave motion is periodic in time.
- At any instant, the form of the wave repeats at equal distances along the direction of wave propagation. Thus, a wave motion is periodic in space.
Thus, a wave motion is doubly periodic.
(ii) What is Doppler Effect?
The apparent change in the frequency of sound heard by a listener, due to the relative motion of the source of sound and the listener, is called the Doppler effect in sound.
(iii) Describe a transverse wave.
A progressive wave in which the vibration of the individual particles of the medium is
perpendicular to the direction of propagation of the wave is called a transverse progressive wave.
Characteristics of a transverse wave:
- Particles vibrate perpendicular to wave propagation direction with same period and amplitude.
- Progressively changing phase of particles forms alternate crests and troughs, forming one cycle.
- No pressure and density variations at any medium point during wave passage.
- Propagation depends on medium's rigidity, requiring modulus of rigidity.
- Waves can only travel through solids and liquid surfaces, not through liquids and gases.
- Vibrations of medium particles lie in the same plane, exhibiting polarization.
(iv) Define a longitudinal wave.
A progressive wave in which the vibration of the individual particles of the medium is along the direction of propagation of the wave is called a longitudinal progressive wave.
Examples:
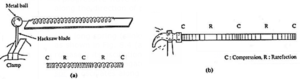
- A long spring (slinky) is attached at one end to a simple oscillatory mechanism, as shown in Fig. (a). When the metal ball is displaced slightly to one side and released, its oscillations periodically compress and extend the spring. As a result, a wave motion propagates along the length of the spring. Since each coil of the spring oscillates along the length of the spring, the wave motion is longitudinal.
- If a long metal bar is periodically struck on one end, Fig. (b), each impact compresses the material of the bar followed by an expansion. The particles of the bar move back and forth and thus a longitudinal wave travels along the bar.
(v) State Newton’s formula for velocity of sound.
Newton's formula for velocity of sound:
v = \(\sqrt{\frac{K}{p}}\)
where v is the wave speed, and p and K are respectively the density and the bulk modulus of the medium.
(vi) What is the effect of pressure on velocity of sound?
According to Laplace's formula, the speed of sound in a gas is
v = \(\sqrt{\frac{γp}{ρ}}\) …..(1)
where p and ρ are the pressure and density of the gas and
ν = CP/CV
In terms of the density of the gas, the equation of state for an ideal gas is written as
\(\frac{p}{ρT}=\frac{R}{M}\) = constant ….(2)
where T is the absolute temperature, R is the universal gas constant and M is the molar mass.
Therefore, at constant T,
\(\frac{p}{ρ}\) = constant …..(3)
Hence, v = \(\sqrt{\frac{γp}{ρ}}\) = constant ……(4)
Thus, at constant temperature, the speed of sound in a gas is independent of the pressure provided the pressure is atmospheric or below, so that the gas closely approximates an ideal gas.
(vii) What is the effect of humidity of air on velocity of sound?
The term humidity is used to express the moisture content in the air. The presence of water vapour in the air affects the density of air which in turn affects the speed of sound in air.
Let vm be the speed of sound in moist air having density ρm and vd the speed of sound in dry air having density ρd.
According to Laplace's formula, vm = \(\sqrt{\frac{γp}{ρ_m}}\) and vd = \(\sqrt{\frac{γp}{ρ_d}}\)
where p is the pressure of air and ν = CP/CV
∴ At constant pressure, \(\frac{v_m}{v_d}=\sqrt{\frac{ρ_d}{ρ_m}}\)
The density of moist air is less than that of dry air.
vm > vd
That is, the speed of sound in moist air is greater than that in dry air.
(viii) What do you mean by an echo?
- An echo is a repetition of the original sound due to reflection from a rigid surface at a distance from the source.
- It can be heard after a time interval in hilly regions or near a reflecting medium.
- Echoes can be heard multiple times due to multiple reflections, but a true echo is a single reflection.
(ix) State any two applications of acoustics.
- Bats use echolocation to navigate and find food in the dark. They emit short ultrasonic pulses (frequency range : 30 kHz to 150 khz). Their echoes give the bats information about obstacles and food.
- Dolphins use echolocation for underwater navigation, location of prey and protection from predators, using subsonic pulses of frequency about 100 Hz.
(x) Define amplitude and wavelength of a wave.
- Amplitude : The magnitude of the maximum displacement of a particle of the medium from its equilibrium position is called the amplitude of the wave.
- Wavelength : It is the distance between consecutive particles of the medium which are moving in exactly the same way at the same time and have the same displacement from their equilibrium positions.
(xi) Draw a wave and indicate points which are (i) in phase (ii) out of phase (iii) have a phase difference of /2.

(i) Points A and E, C and G, B and F, D and H are in phase.
(ii) Points A and C, B and D, C and E, D and F, E and G, F and H, are out of phase.
(iii) Points A and B, B and C, C and D, D and E, E and F, F and G, G and H have a phase difference of /2 radian.
(xii) Define the relation between velocity, wavelength and frequency of wave.
During the passage of a progressive wave through a medium, the wave advances a
distance equal to the wavelength λ. in the periodic time T of the vibration of the particles of the medium. Then, the speed of propagation (the magnitude of the velocity) of the wave is
v = λ/T
The frequency n of the progressive wave is equal to the reciprocal of the period :
n = 1/T (2)
From Eqs. (1) and (2), we have,
v = n λ . i.e., wave speed = frequency x wavelength
This relation is true for all types of progressive wave.
(xiii) State and explain principle of superposition of waves.
Principle of superposition of waves: When two or more waves arrive at the same time at a point, the resultant displacement at that point, at that instant, is the vector sum of the displacements due to each wave acting independently.
Explanation: Consider two waves travelling in a medium arriving simultaneously at a point P.
Let y1 and y2 be the displacements due to the two waves at the point. Then, according to the principle of superposition of waves, the resultant displacement at the point is \(\vec{y_R}=\vec{y_1}+\vec{y_2}\)
This implies that, depending upon the phase difference between the two waves,
yR (maximum) = |y1| + |y2 | and
yR (minimum) = |y1| — |y2 |
(xiv) State the expression for apparent frequency when source of sound and listener are
(i) moving towards each other
(ii) moving away from each other
Let n ≡ apparent frequency of sound,
n0 ≡ actual frequency of sound,
v ≡ speed of sound in air,
v ≡ speed of the source of sound and
vL ≡ speed of the listener
(i) For the source and listener moving towards (approaching) each other,
n = n0 \([\frac{v+v_L}{v-v_s}]\)
(ii) For the source and listener moving away (receding) from each other,
n = n0 \([\frac{v-v_L}{v+v_s}]\)
(xv) State the expression for apparent frequency when source is stationary and listener is
(i) moving towards the source
(ii) moving away from the source
Let n ≡ apparent frequency of sound,
n0 ≡ actual frequency of sound
v ≡ speed of sound in air and
vL ≡ speed of the source of sound
(i) The apparent frequency when the source is moving towards (approaching) the stationary listener is
n = n0 \([\frac{v+v_L}{v}]\)
(ii) The apparent frequency when the source is moving away (receding) from the stationary listener is
n = n0 \([\frac{v-v_L}{v}]\)
(xvi) State the expression for apparent frequency when listener is stationary and source is.
(i) moving towards the listener
(ii) moving away from the listener
Let n ≡ apparent frequency of sound,
n0 ≡ actual frequency of sound
v ≡ speed of sound in air and
vs ≡ speed of the source of sound
(i) The apparent frequency when the source is moving towards (approaching) the stationary listener is
n = n0 \([\frac{v}{v-v_s}]\)
(ii) The apparent frequency when the source is moving away (receding) from the stationary listener is
n = n0 \([\frac{v}{v+v_s}]\)
(xvii) Explain what is meant by phase of a wave.
Let us consider propagation of a mechanical wave. We shall consider a simple case where the wave travels along the positive x-axis and the displacement (y) of a particle of the medium from its equilibrium position is given by
y(x,t) = a sin\((\frac{2π}{λ}x+2πnt+Φ)\)
Here, a is the amplitude, A is the wavelength and n is the frequency of wave motion. x denotes the equilibrium position of the particle and t denotes time. is a constant. y may be along the x axis or perpendicular to it.
In this case, the state of oscillation of a particle of the medium is called the phase of the particle and also of the wave.
The quantity \((\frac{2π}{λ}x+2πnt+Φ)\) is the phase of the particle at time t.
To describe the phase of a particle at a place, its displacement, direction of velocity and oscillation number are required.

In above Fig. particles O and E or Q and L or H and D or P and K or G and C, etc. have the same displacement I as well as direction of velocity. These particles are said to be in phase during their respective oscillations. Particles O and G, Q and P, have the same displacement but the directions of their velocity are opposite. These particles are said to be out of phase during their respective oscillations.
Successive particles having the same phase differ by 1 in their oscillation number. Thus, if particle F is at its nth oscillation, particle B is at its (n + 1)th oscillation.
(xviii) Define progressive wave. State any four properties.
(a) Progressive wave : A wave motion or a progressive wave is a state of disturbance in which energy is propagated from one place to another at a finite speed without propagation of matter. It is also called a travelling wave.
(b) Properties of a progressive wave : Amplitude, wavelength, period, double periodicity, frequency and wave speed are the properties of a progressive wave.
(xix) Distinguish between transverse waves and longitudinal waves.
| Transverse Waves | Longitudinal Waves |
| The medium's particles vibrate perpendicular to the wave's propagation direction. | The particles of the medium vibrate along the direction of propagation of the
wave. |
| Typical alternate crests and troughs are formed. | Typical alternating areas of compression and rarefaction are generated. |
| There are no pressure and density variations in the medium. | Periodic compressions and rarefactions in space and time cause periodic pressure and density fluctuations in the medium. |
| For propagation of a transverse wave, the medium must be able to resist shear, i.e., it must possess the modulus of rigidity. | For propagation of a longitudinal wave, the medium must be able to resist change in volume, i.e., it must possess the bulk modulus. |
| They can travel through solids and on surfaces of liquids only. They cannot travel through liquids and gases. | They can travel through any material medium i.e., solid, liquid or gas. |
| Transverse waves exhibit polarization and can be polarized. | The question of polarization does not
arise. |
(xx) Explain Newton’s formula for velocity of sound. What is its limitation?
(a) Newton (in 1687) derived the relation between the speed of sound, and the inertia and the elastic property of the medium:
v = \(\sqrt{\frac{K}{ρ}}\)
where v is the wave speed ‘(speed of sound) and ρ and K are respectively the density and the bulk modulus of the medium.
Assumptions: For a theoretical estimate of the speed of sound in air, Newton assumed that the air obeyed Boyle's law and that the pressure variations caused by the passage of the waves are slow and take place isothermally. Newton's formula: Newton, therefore, used the isothermal bulk modulus, which, for an ideal gas, is equal to the pressure p of the gas. So, the expression he deduced for the speed of sound in air is
v = \(\sqrt{\frac{K_{isothermal}}{ρ}}\) = \(\sqrt{\frac{p}{ρ}}\)
This is Newton's formula for the speed of sound in an ideal gas.
(b) At NTP, p = 1.013 x 105 Pa and
pair = 1.293 kg/m3, so that
v = \(\sqrt{\frac{1.013×10^5\,Pa}{1.293\,kg/m^3}}\) = 280 m/s
Limitation: At NTP, the value of speed of sound given by Newton's formula (280 m/s) is significantly less (by about 16%) than the experimental value of 331.3 m/s.
Question 3. Solve the following problems.
(i) A certain sound wave in air has a speed 340 m/s and wavelength 1.7 m for this wave, calculate (a) the frequency (b) the period.
Given: v = 340 m/s, λ = 1.7 m
(1) The frequency of the wave, n = \(\frac{v}{λ}\) = \(\frac{340}{λ}\) = 200 Hz
(2) The period of the wave, T = \(\frac{1}{n}\) = \(\frac{1}{200}\) = 5 x 10-3 s
(ii) A tuning fork of frequency 170 Hz produces sound waves of wavelength 2 m. Calculate speed of sound.
Given : n =170 Hz, λ = 2 m
The speed of sound, v = nλ = 170 x 2 = 340 m/s
(iii) An echo-sounder in a fishing boat receives an echo from a shoal of fish 0.45 s after it was sent. If the speed of sound in water is 1500 m/s, how deep is he shoal?
Given : Total time, 2t = 0.45 s ∴ t = 0.225 s, v = 1500 m/s
s = v t = (1500) (0.225) = 337.5 m
The shoal is 337.5 m deep.
(iv) A girl stands 170 m away from a high wall and claps her hands at a steady rate so that each clap coincides with the echo of the one before.
(a) If she makes 60 claps in 1 minute, what value should be the speed of sound in air?
(b) Now, she moves to another location and finds that she should now make 45 claps in 1 minute to coincide with successive echoes. Calculate her distance for the new position from the wall.
(a) 60 claps in 1 minute, ∴ 1 clap in 1 second
In Fig.
S = GW = 170 m
v = \(\frac{distance}{time} = \frac{GW+WG}{time}\) = \(\frac{170+170}{1}\) = 340 m/S
This is the speed of sound in air.

(b) Let G’ correspond to the location in part (b)
Her 45 claps in 1 minute ∴ 1 clap corresponds to \(\frac{60}{45}\)s = \(\frac{4}{3}\)s
In this case, G‘W + WG' = 2G‘W = vt
= 340 × \(\frac{4}{3}\) = \(\frac{340×4}{3}\) m
G‘W = \(\frac{340×4}{3×2}\) = \(\frac{340×2}{3}\) = \(\frac{680}{3}\) = 226.7 m
This is the required distance.
(If we take 40 claps in 1 minute then answer = 255m as per textbook)
(v) Sound wave A has period 0.015 s, sound wave B has period 0.025. Which sound has greater frequency?
Given : TA = 0.015 s, TB = 0.025 s
Frequency, n = \(\frac{1}{T}\)
Here, TA < TB ∴ nA > nB
Sound wave A has greater frequency
(vi) not given in textbook.
(vii) At what temperature will the speed of sound in air be 1.75 times its speed at N.T.P?
Given : v = 1.75v0, T0= 273 K
v = \(\sqrt{\frac{rRT}{M}}\) and v0 = \(\sqrt{\frac{rRT_0}{M}}\)
\(\frac{v}{v_0}\)= \(\sqrt{\frac{T}{T_0}}\)
∴ \(\frac{T}{T_0}\) = \((\frac{v}{v_0})^2\)
∴ T = \(T_0(\frac{v}{v_0})^2\)
= 273(1.75)2 = 836.1 K
= 836.1 − 273 = 563.1 °c
(viii) A man standing between 2 parallel cliffs fires a gun. He hears two echoes one after 3 seconds and other after 5 seconds. The separation between the two cliffs is 1360 m, what is the speed of sound?
Given : 2t1 = 3 s, ∴ t1 = 1.5 s, 2t2 = 5 s, ∴ t2 = 2.5 s,
s1+ s2 = 1360 m
s1 = vt1 = 1.5 v and s2 = vt2 = 2.5v
∴ s1 + s2 = 1.5 v+ 2.5 v = 4v
v = \(\frac{s_1+s_2}{4}=\frac{1360}{4}) = 340m/s
340 m/s is the speed of sound in air.
(ix) If the velocity of sound in air at a given place on two different days of a given week are in the ratio of 1:1.1. Assuming the temperatures on the two days to be same what quantitative conclusion can your draw about the condition on the two days?
Given : \(\frac{v_1}{v_2}\) = \(\frac{1}{1.1}\)
v = \(\sqrt{\frac{γp}{ρ}}\), v1 = \(\sqrt{\frac{γp}{ρ_1}}\) and v2 = \(\sqrt{\frac{γp}{ρ_2}}\)
for the same pressure
∴ \(\frac{v_2}{v_1}\) = \(\sqrt{\frac{ρ_1}{ρ_2}}\)
∴ \(\sqrt{\frac{ρ_1}{ρ_2}}\) = (1.1)2 = 1.21
Thus, ρ1 = 1.21ρ2, where ρ1 and ρ2 are the densities of air on the two days.
(x) A police car travels towards a stationary observer at a speed of 15 m/s. The siren on the car emits a sound of frequency 250 Hz. Calculate the recorded frequency. The speed of sound is 340 m/s.
Given : vs = 15 m/s, v = 340 m/s, n0 = 250 Hz
n = n0\((\frac{v}{v-v_s})\) = (250)\((\frac{340}{340-15})\)
= \(\frac{250×340}{325}\) = \(\frac{3400}{13}\)
= 261.54 Hz
This is the recorded (apparent) frequency.
(xi) The sound emitted from the siren of an ambulance has frequency of 1500 Hz. The speed of sound is 340 m/s. Calculate the difference in frequencies heard by a stationary observer if the ambulance initially travels towards and then away from the observer at a speed of 30 m/s.
Given : n0 = 1500 Hz, v = 340 m/s, vs = 30 m/s
n = n0\((\frac{v}{v-v_s})\) = (1500)\((\frac{340}{340-30})\)
= \(\frac{1500×340}{310}\) = 1645 Hz
(as the ambulance moves towards the stationary observer)
n = n0\((\frac{v}{v+v_s})\) = (1500)\((\frac{340}{340+30})\)
= \(\frac{1500×340}{370}\) = 1378 Hz
(as the ambulance moves away from the stationary observer)
The difference in frequencies
= n1 − n2 = 1645 − 1378
= 267 Hz
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 7: Thermal Properties of Matter – Online Solution
Next Chapter : Chapter 9: Optics – Online Solution
We reply to valid query.