Notes-Part-2
Topics to be Learn : Part-2
|
Absorption, Reflection and Transmission of Heat Radiation
Modes of heat transfer : The three modes of heat transfer are conduction, convection and radiation.
Conduction : Conduction is the mode of heat transfer within a body or between two bodies in contact, from a region of high temperature to a region of lower temperature without the migration of the particles of the medium.
Convection : Convection is the mode of heat transfer from one part of a fluid to another by the migration of the particles of the fluid.
Radiation : Radiation is the mode of heat transfer by electro-magnetic waves / quanta. Example : The transfer of heat and light from the Sun to the earth and to us.
The first two modes of heat transfer require a material medium for transmission of heat but radiation does not need a material medium.
Thermal radiation or heat radiation : Radiation is the mode of heat transfer or in general, energy transfer by electromagnetic waves / quanta.
Thermal radiation or heat radiation is the radiation produced by thermal agitation of the particles of a body, and its spectrum, i.e., frequency distribution or wavelength distribution, is continuous from the far infrared to the extreme ultraviolet region depending on the temperature of the body.
Properties :
- Thermal radiations are electromagnetic waves/quanta extending from the far infrared to the extreme ultraviolet region. In this spectrum, the infrared waves (wavelengths ranging from about 700 nm to about 1 mm) are sensed as heat.
- They have the same speed in free space as that of light, nearly 3x108 m/s, which makes radiation the most rapid mode of heat transfer.
- They exhibit all the optical phenomena of light, viz. reflection, absorption, refraction, interference, diffraction and polarization.
- Radiation incident on a body is, in general, partly reflected, partly absorbed and partly transmitted.
- Thermal radiation obeys the inverse-square law of intensity, i.e., the intensity at a point is inversely proportional to the square of its distance from a point source of radiation.
Coefficients of absorption : The coefficient of absorption or absorptive power or absorptivity of a body is the ratio of the quantity of radiant energy absorbed by the body to the quantity of radiant energy incident on the body in the same time.
Coefficient of reflection : The coefficient of reflection or reflectance or reflective power of the surface of a body is the ratio of the quantity of radiant energy reflected by the surface to the quantity of radiant energy incident on the surface in the same time.
Coefficient of transmission : The coefficient of transmission or transmittance or of a bod is the ratio of the transmissive power quantity of radiant energy transmitted by the body to the quantity of radiant energy incident on the body in the same time.
Relation between the coefficients of absorption, reflection and transmission :
Let Q be the quantity of radiant energy incident on a body and Qa, Qr and Qt be the quantities of radiant energy absorbed, reflected and transmitted by the body respectively, in the same time. Since the total energy is conserved, we have,
Qa + Qr + Qt = Q
∴ \(\frac{Q_a}{Q}+\frac{Q_r}{Q}+\frac{Q_t}{Q}\) = 1
∴ \(\frac{Q_a}{Q}\) = a ……. coefficient of absorption
∴ \(\frac{Q_r}{Q}\) = r …….. coefficient of reflection
∴ \(\frac{Q_t}{Q}\) = t ………… coefficient of transmission
Hence + r + t =1 This is the required relation.
Since all the three quantities a, r and t are ratios of thermal energies, they are dimensionless quantities.
- If r = 0 and a = 0, then t = 1, all the incident energy is transmitted through the object i.e., it is a perfect transmitter. The object is said to be completely transparent to the radiation.
- If t = 0 and a = 0, then r = 1, all the incident energy is reflected by the object i.e., it is a perfect reflector. A good reflector is a poor absorber and a poor transmitter.
- If r = 0 and t = 0 then a = 1, all the incident energy is absorbed by the object. Such an object is called a perfect blackbody.
| The coefficients of absorption, reflection and transmission are, respectively, the measures of the body or material to absorb, reflect or transmit radiation.
They are dimensionless quantities and have no units. They depend on the material and physical conditions of the body as well as on the Frequency of the incident radiation. |
Athermanous substances : A substance which is largely opaque in radiations, i.e., a substance which does not transmit heat radiations incident on it is known as an athermanous substance.
Examples : Water, wood, iron, copper, moist air, benzene are athermanous substances.
Diathermanous substances : A substance through which heat radiations can pass is known as a diathermanous substances.
Examples : Quartz, sodium chloride, hydrogen, oxygen, dry air, carbon tetrachloride are diathermanous substances.
Explain : A Substance may be athermanous or diathermanous for certain wavelength ranges while good absorber for other wavelength ranges.
For interaction of light with matter, it is necessary to consider the atomic nature of matter. Interaction of an atom with light depends on the frequency or equivalently on the photon energy. An atom absorbs light if the photon’s energy equals one of the excitation energies of the atom. In the dense atomic neighbourhood of ordinary gases at pressures above 100 Pa, solids and liquids, the discrete atomic energy states widen into bands. Thus, bulk matter, depending on its nature, possesses absorption bands in specific regions within the electromagnetic frequency spectrum. Radiant energy of other frequencies is elastically scattered so that the material is transparent at these frequencies.
Perfect blackbody : A perfect blackbody or simply a blackbody is defined as a body which absorbs all the radiant energy incident on it.
Fery’s Blackbody: Fery designed a spherical blackbody which consists of a hollow double—walled, metallic sphere provided with a tiny hole or aperture on one side,
See Fig.
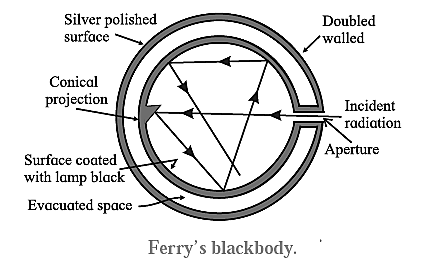
The inside wall of the sphere is blackened with lampblack while the outside is silver-plated. The space between the two walls is evacuated to minimize heat loss by conduction and convection. Any radiation entering the sphere through the aperture suffers multiple reflections where about 97% of it is absorbed at each incidence by the coating of lampblack. The radiation is almost completely absorbed after a number of internal reflections. A conical projection on the inside wall opposite the hole minimizes probability of incident radiation escaping out.
- When the sphere is placed in a bath of suitable fused salts, so as to maintain it at the desired temperature, since the hole in Fery’s blackbody is very small, the radiations from the inner surface are well mixed up by reflection before they can escape. Hence, when Fery’s blackbody is placed in a high-temperature bath of fused salts, the hole serves as the source of blackbody radiation. The intensity and the nature of the radiation depend only on the temperature of the walls.
- The outer surface of Fery’s blackbody is made highly reflective and lampblack too has a small coefficient of reflection. Hence, neither of them alone is a blackbody.
- A blackbody, by definition, has coefficient of absorption equal to 1. Hence, its coefficient of reflection and coefficient of transmission are both zero.
- The radiation from a blackbody, called blackbody radiation, covers the entire range of the electromagnetic spectrum. Hence, a blackbody is called a full radiator.
Cavity radiator : A cavity radiator is a block of material with internal cavity. The inner and outer surfaces of the block are connected by a small hole. Most of the radiant energy entering the block through the hole cannot escape from the hole. The block, therefore, acts almost like a blackbody.
Cavity radiation : When the cavity radiator is heated to high temperature, radiation coming out from the hole resembles blackbody radiation. It is called cavity radiation.
It depends only on the temperature of the radiator and not on the shape and size of the cavity as well as the material of the walls of the cavity.
Prevost’s theory of exchange of heat : In 1792, Pierre Prevost put forward a theory of exchange of heat. According to this theory, all bodies at all temperatures above the absolute zero temperature (0K) radiate thermal energy to the surroundings and at the same time receive radiant energy from the surroundings. Thus, there is continuous exchange of radiant energy between a body and its surroundings.
The quantity of radiant energy (thermal energy) emitted by a body per unit time depends upon the nature of the emitting surface, the area of the surface and the temperature of the surface. The quantity of radiant energy absorbed by a body per unit time depends upon the nature of the absorbing surface, the area of the surface and the time rate at which the radiant energy is incident on the body.
- If the time rate of emission of thermal energy is greater than the time rate of absorption of thermal energy, the temperature of the body falls.
- If the emission rate is less than the absorption rate, the temperature of the body increases.
- If the emission rate equals the absorption rate, the temperature of the body remains constant.
A body appears red if its temperature is around 800°C, and white hot if its temperature is around 3000 °C.
Emissive power or radiant power : Emissive power or radiant power of a body (symbol, R) : The emissive power of a body at a given temperature is defined as the quantity of radiant energy emitted by the body per unit time per unit surface area of the body at that temperature.
Coefficient of emission (or emissivity) of a body (symbol, e) : The coefficient of emission (or emissivity) of a body is defined as the ratio of the emissive power of the body (R) to the emissive power of a perfect blackbody (Rb) at the same temperature as that of the body.
e=R/Rb
The SI unit and dimensions of emissive power are the watt per square metre (W/m2 Or Js-1m-2) and [M1L0T-3]. The coefficient of emission is a dimensionless and unit less quantity. For a perfect blackbody, e =1 and for a perfect reflector, e = 0.
Q. Why are the bottom of cooking utensils blackened and tops polished?
The bottoms of cooking utensils are blackened to increase the rate of absorption of radiant energy and tops are polished to increase the reflection of radiation.
Q. A car is left in sunlight with all its windows closed on a hot day. After some time it is observed that the inside of the car is warmer than outside air. Why?
The air inside the car is trapped and hence is a bad conductor of heat.
Q. If surfaces of all bodies are continuously emitting radiant energy, why do they not cool down to 0 K ?
Bodies absorb radiant energy from the surroundings.
Kirchhoff’s law of heat radiation: At a given temperature, the ratio of the emissive power to the coefficient of absorption of a body is equal to the emissive power of a perfect blackbody at the same temperature for all wavelengths. OR
For a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity.
Proof : Consider an ordinary body A and perfectly black body B of the same dimension suspended in a uniform temperature enclosure as shown in the figure.
At thermal equilibrium, both the bodies will have the same temperature as that of the enclosure.
Let, E = emissive power of ordinary body A
Eb = emissive power of perfectly black body B
a = coefficient of absorption of A
e = emissivity of A
Q = radiant energy incident per unit time per unit area on each body Quantity of heat absorbed per unit area per unit time by body
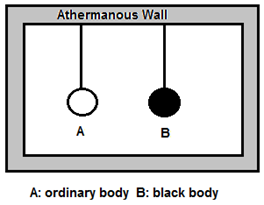
Body A will absorb the quantity aQ per unit time per unit surface area and radiate the quantity R per unit time per unit surface area. Since there is no change in its temperature, we must have,
aQ = E .. (1)
As body B is a perfect blackbody, it will absorb the quantity Q per unit time per unit surface area and radiate the quantity R, per unit time per unit surface area.
Since there is no change in its temperature, we must have,
Q=Eb ... (2)
From Eqs. (1) and (2), we get,
a = E/Q = E/Eb …….. (3)
From Eq. (3), we get, E/a= Eb
But by definition of coefficient of emission
e =E/Eb …….. (4)
from eq. 3 & 4 we get
e=a
Hence the proof of kirchoff’s law of radiation
Spectral distribution of blackbody radiation :
Blackbody radiation is the electromagnetic radiation emitted by a blackbody by virtue of its temperature. It extends over the whole range of wavelengths of electromagnetic waves.
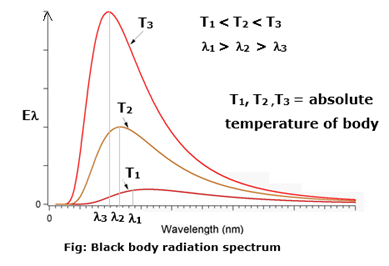
The distribution of energy over this entire range as a function of wavelength or frequency is known as the spectral distribution of blackbody radiation or blackbody radiation spectrum see Fig.
If Eλ is the emissive power of a blackbody in the wavelength range λ and λ+dλ, the energy it emits per unit area per unit time in this wavelength range depends on its absolute temperature T, the wavelength l and the size of the interval dl.
Characteristics of blackbody radiation spectrum :
- The emissive power R; for every wavelength λ increases with increasing temperature.
- Each curve has a characteristic form with a maximum for Rλ at a certain wavelength λm.
- λm depends on the absolute temperature of the body and, with increasing temperature, shifts towards shorter wavelengths, i.e., towards the ultraviolet end of the spectrum.
- λmT = a constant.
- The area under each curve gives the total radiant power per unit area of a blackbody at that temperature and is proportional to T4, (Stefan-Boltzmann law).
| The idea of quantization of energy was first proposed by Planck to explain the blackbody spectrum or the cavity radiations. Planck proposed a model in terms of the atomic processes. He considered the atoms of the walls of the cavity as tiny electromagnetic oscillators with characteristic frequencies that exchange energy with the cavity. This energy was supposed to have only specific values E = nhν, where ν is the frequency of oscillator, h is a universal constant that has a value 6.626 × 10-34 J s and n can take only positive integral values. The oscillators
would not radiate energy continuously but only in “jumps” or “quanta” corresponding to transitions from one quantized level of energy to another of lower energy. As long as the oscillator is in one of the quantized states, it does not emit or absorb energy. This model of Planck turned out to be the basis for Einstein’s theory to explain the observations of experiments on photoelectric effect, as you will learn in Chapter 14. |
Wien’s displacement law : The wavelength for which the emissive power of a blackbody is maximum, is inversely proportional to the absolute temperature of the blackbody.
OR
For a blackbody at an absolute temperature T, the product of T and the wavelength λm corresponding to the maximum radiation of energy is a constant.
Tλm = b, is constant.
(**The value of the constant b in Wien’s displacement law is 2.898 x 10-3 m-K)
Significance of Wien's displacement law :
- It can be used to estimate the surface temperature of stars.
- It explains the common observation of the change of colour of a solid on heating from dull red (longer wavelengths) to yellow (smaller wavelengths) to white (all wavelengths in the visible region).
The Stefan-Boltzmann law : The rate of emission of radiant energy per unit area or the power radiated per unit area of a perfect blackbody is directly proportional to the fourth power of its absolute temperature. OR
The quantity of radiant energy emitted by a perfect blackbody per unit time per unit surface area of the body is directly proportional to the fourth power of its absolute temperature.
The power per unit area radiated from the surface of a blackbody at an absolute temperature T is its emissive power or radiant power Rb at that temperature. According to the Stefan-Boltzmann law,
Rb ∝ T4 , ∴ Rb = σT4
where the constant σ is called Stefan's constant.
If A is the surface area of the body, its radiant power, i.e., energy radiated per unit time, is AσT4 (σ=5.67 x 10-8 W/m2.K4 )
Q. Derive an expression for the net rate of loss of heat per unit area by a perfect blackbody in a cooler surroundings.
Consider a perfect blackbody at absolute temperature T. We assume its surroundings also to act as a perfect blackbody at absolute temperature T0, where To < T. The power per unit area radiated from the surface of a blackbody at temperature T is its emissive power Rb at that temperature. According to the Stefan-Boltzmann law, Rb = σT4 where s is the Stefan constant. At the same time, the body absorbs radiant energy from the surroundings. The radiant energy absorbed per unit time per unit area by the black-body is σT04 Therefore, the net rate of loss of radiant energy per unit area by the blackbody is σ(T4— T04). If the body at temperature T has emissivity e < 1, (i.e. it is not a perfect blackbody ) the net rate of loss of radiant energy per unit area is eσ (T4— T04).
Useful notes