Chapter-5-Chemical Bonding
Maharashtra State Board-Class-11-Science-Chemistry-Chapter -5
Notes Part-3
Topics to be Learn : Part-3
|
Molecular orbital theory :
In some cases valence bond theory gives to incorrect electronic description. Therefore another bonding description called Molecular Orbital Theory (MO) has been introduced.
Features of molecular orbital theory (MOT):
- In a molecule, the electrons are present in various molecular orbitals similar to the electrons in atoms which are present in various atomic orbitals.
- The atomic orbitals of proper symmetry and comparable energies combine to form the molecular orbitals.
- An electron in an atomic orbital is influenced by one nucleus hence atomic orbital is monocentric. While the electron in a molecular orbital is influenced by two or more nuclei depending upon the number of atoms in the molecule, hence, the molecular orbital is polycentric.
- The number of molecular orbitals formed is equal to the number of combining atomic orbitals.
- Two combining atomic orbitals result in the formation of two molecular orbitals, of which one is known as bonding orbital having higher energy and the other is known as antibonding orbital having lower energy.
- The molecular orbitals like atomic orbitals are filled in accordance with the aufbau principle,
- Pauli’s exclusion principle and Hund’s rule of maximum multiplicity.
Formation of molecular orbitals :
According to the MO theory the formation of molecular orbitals from atomic orbitals is expressed in terms of Linear Combination of Atomic Orbitals (LCAO).
Formation of molecular orbitals by a method of linear combination of atomic orbitals (LCAO method) :
- According to wave mechanics, the atomic orbitals can be expressed by wave functions (Ψ).
- The nature of a molecular orbital can be obtained by combining the atomic orbitals of bonding atoms forming a molecule.
- Due to nuclear attraction, the bonding electrons are most likely in the vicinity of the nuclei.
- Consider the atomic orbitals ΨA and ΨB of comparable energies and same symmetry of two bonding atoms A and B respectively.
- By combining these atomic orbitals, (hence, called linear combination) two molecular orbitals Ψa and Ψb are obtained.
- Two atomic orbitals combine in two ways to form molecular orbitals. (i) By addition of their wave functions. (ii) By subtraction of their wave functions, mathematically described as follows :
Ψb = ΨA + ΨB
Ψa = ΨA − ΨB
- Where, Ψb and Ψa are the wave functions of bonding molecular orbital and antibonding molecular orbital respectively.
- For bonding process, two atoms come closer to one another. The atomic orbitals overlap forming two molecular orbitals (M.O.s) one with the lower energy and the other with higher energy than the combining atomic orbitals.

- The molecular orbital with lower energy gives rise to attractive state and more stability and it is called bonding molecular orbital, Ψb
- The molecular orbital with higher energy gives rise to a repulsive state, hence decreases the stability and it is called antibonding molecular orbital, Ψa.
Conditions for the combination of Atomic Orbitals :
Atomic orbitals can be combined linearly which give molecular orbitals only if following conditions are fulfilled.
(i) The combining atomic orbitals must have comparable energies.
- So 1s orbitals of one atom can combine with 1s orbital of another atom but not with 2s orbital, because energy of 2s orbital is much higher than that of 1s orbital.
(ii) The combining atomic orbitals must have the same symmetry along the molecular axis. Conventially z axis is taken as the internuclear axis. So even if atomic orbitals have same energy but their symmetry is not same they cannot combine.
- For example, 2pz orbital of an atom can combine only with 2pz orbital of another atom, and not with 2px or 2py orbital of that atom because the symmetries are not same. pz is symmetrical along z axis while px is symmetrical along x axis.
(iii) The combining atomic orbitals must overlap to the maximum extent. Greater the overlap, greater is the electron density between the nuclei and so stronger is the bond formed.
Formation of Bonding molecular orbital (BMO) :
- Every atomic orbital is represented by a wave function Ψ which may have + ve or −ve sign. Ψ2 represents the probability of electron density in the region near nuclei. Ψ2 is always positive.
- This molecular orbital (M.O.) is formed by (linear) combination of two atomic orbitals represented by ΨA and ΨB with the same sign, from two bonding atoms A and B respectively and represented as ΨMO or Ψb or σ.
- This may be represented mathematically as the addition of two wave functions.
ΨMO = σ = ΨA + ΨB
- In bonding molecular orbital, the overlapping of the atomic orbitals takes place in the region between two nuclei along the internuclear axis.
- The energy of the bonding molecular orbital is lower than that of the parent bonding atoms.

Formation of Antibonding molecular orbital (AMO) :
- This molecular orbital is formed by (linear) combination of two atomic orbitals represented by ΨA and ΨB with opposite signs from two bonding atoms A and B respectively and represented as ΨAMO or Ψa or σ*.
- This is mathematically represented as the subtraction of two wave functions.
ΨAMO = σ* = ΨA + ΨB
- This molecular orbital splits into two lobes with a nodal plane at the centre.
- The electrons lie in the region in space where they are not under attraction of both nuclei.
- The energy of the antibonding molecular orbital is higher than that of parent bonding atoms.
Types of molecular orbitals :
In diatomic molecules, molecular orbitals formed by combination of atomic orbitals are of two types (i) σ (ii) π.
(i) Sigma molecular orbital (σ) :
- When the atomic orbitals overlap along the line joining the two nuclei (head-on) a sigma molecular orbital (σ) is formed.
- The sigma molecular orbital is cylindrically symmetrical along the internuclear axis.

Pi molecular orbital (π) :
- When the atomic orbitals overlap collaterally, a pi (π) molecular orbital is formed.
- These molecular orbitals have internuclear axis lying in a nodal plane.

Energy levels and electronic configuration :
- We know on combination of two 1s orbitals; two molecular orbitals σ1s and σ*1s are formed. Similarly two 2s orbitals yield σ*2s and σ2s molecular orbitals.
- The three 2p orbitals on one atom combine with three 2p orbitals on another atom forming six molecular orbitals, designated as σ2pz, πpx, πpy and σ*2pz, π*px, π*py
Variation in energy levels for molecular orbitals in homonuclear diatomic molecules :
The molecular orbitals in homonuclear diatomic molecules have been determined experimentally.
- For diatomic molecules of second row elements except O2 and F2 the rank order of energies is : σ1s < σ*1s < σ2s < σ*2s < π2px = π2py > < σ2pz < (π*2py = π*2px) < σ*2pz
- For O2 and F2 increasing order of energies was found to be : σ1s < σ*1s < σ2s < σ*2s < σ2pz < (π 2px = π2py) < (π*2px = π*2py) < σ*2pz
The sequence of filling the molecular orbitals (MO) give electronic configuration of molecules. The electronic configuration of molecules provides the following information.
- Stability of molecules
- Magnetic nature of molecules
- Bond order of a molecule.
(i) Stability of molecules : If in a molecule the number of electrons in bonding MOs is greater than the number of electrons in antibonding MOs, then the molecule is stable.
(ii) Magnetic nature of molecules : If all MOs in a molecule are completely filled with two electrons each with opposite spins, then their spin moments are cancelled and the molecule is diamagnetic and repelled by magnetic field. However if one or more MOs are half filled with one electron, then the molecule is paramagnetic and attracted by magnetic field.
(iii) Bond order of a molecule : Bond order is defined as one half the difference between the number of electrons present in the bonding (Nb) and the antibonding (Na) molecular orbitals.
Bond order = \(\frac{N_b-N_a}{2}\)
A positive value of bond order indicates a stable molecule while zero or negative bond order indicates an unstable molecule.
Key ideas of MO theory :
- Molecular orbitals (MOs) are formed by combining AOs of different atoms of comparable energies and proper symmetry.
- Molecular orbital describes the region of space in the molecule representing the probability of an electron.
- MOs those are lower in energy than AOs are bonding (σ) MOs while those higher in energy are antibonding (σ*) MOs.
- Only two electrons with opposite spins occupy each MO.
- The electrons are filled in increasing order in MOs beginning with the lowest energy.
- The bond order of the molecule can be calculated from the number of bonding and antibonding electrons.
- The stability of the molecule can be explained.
MO description of simple diatomic Molecules :
Formation of H2 molecule on the basis of MOT :
- Hydrogen atom has electronic configuration, 1H = 1s1.
- H2 molecule is formed by linear combination of two 1s atomic orbitals of two H atoms, each containing one unpaired electron with opposite spins.

- Two molecular orbitals (bonding) σ1s and (anti-bonding) σ*1s are formed by linear combination of atomic orbitals.
- Two electrons in H2 are present in bonding molecular orbital, σ1s of lower energy. Hence the electronic configuration of H2 is σ1s2.
- There are no electrons in the antibonding molecular orbital σ*1s.
- Bond order = \(\frac{N_b-N_a}{2}\)=\(\frac{2-0}{2}=1\), Hence, two H atoms are bonded by a single bond.
*Q. Helium is always monoatomic. Explain on the basis of MOT.
- He atom has electronic configuration, 2He = 1s2.
- Each He atom has 2 electrons, hence He2 molelecule would have 4 electrons.
- Two molecular orbitals namely bonding σ1s and antibonding σ*1s are formed.
- Out of 4 electrons, bonding molecular orbital σ1s will accommodate 2 electrons and antibonding olecular orbital σ*1s will accommodate 2 electrons with opposite spins.
- The electronic configuration of He2 will be He2 σ1s2, σ*1s2.

- Bond order = \(\frac{N_b-N_a}{2}\)=\(\frac{2-0}{2}=1\)
- Since the bond order is zero, He; molecule is unstable and hence it does not exist. Therefore, He is always monoatomic.
Stability of Li2 molecule and its diamagnetic character :
- Li atom has electronic configuration, Li(3) = 1 s2, 2s2.
- Each Li atom has 3 electrons, hence, Liz molecule has 6 electrons.
- Formation of molecular orbitals (MOS) : Linear combination of two atomic orbitals give two molecular orbitals namely bonding σ and antibonding σ* :
- Linear combination of atomic orbitals gives four molecular orbitals σ1s, σ*1s, σ2s, σ*2s

- σ1s and σ*1s being inner MOs, do not contribute towards net chemical bonding hence they are also designated as KK shells. Therefore, the electronic configuration of Li2 molecule is represented as Li2 σ1s2. σ*1s2 σ2s2 OR KK σ2s2
- Bond order=(4-2)÷2=1,
- This means in Li2 molecule there is one bond between the two Lithium atoms.
- Such Li2 molecules are found in the vapour state. As there are no unpaired electrons the molecule is diamagnetic.
Formation of N2 molecule on the basis of MOT :
- N atom has electronic configuration N(7) = 1s2 2s2 2px1 2py1 2pz1
- Each N atom has 7 electrons, hence N2 molecule has 14 electrons.
- Formation of molecular orbitals : Linear combination of atomic orbitals give molecular orbitals namely bonding σ or π and antibonding σ* or π*.

- Since N is a light atom, the energy of degenerate MOs, π2py and πpz is lower than σ2px. Hence, the electronic configuration of N2 molecule is, (σ1s2 σ*1s2) (σ2s2 σ*2s2) (π2py2=π2pz2) σpx2
- Bond order=(10-4)÷2=3,
- Hence N2 molecule has the highest bond order of 3 and there is a triple bond, one sigma and two π bonds between two N atoms. Therefore, N2 is the most stable molecule among the series.
- Since there is no unpaired electron, N2 molecule is diamagnetic.
| Know This :
Among diatomic molecules the bond order and bond enthalpy of N2 is highest. Bond order = 3, Bond enthalpy = 946 kJ mol-1. |
Formation of O2 molecule with the help of MOT OR Paramagnetic character of O2 molecule :
- Oxygen atom has electronic configuration, O(=8) = 1s2 2s2 2px2 2py1 2pz1
- Each O atom has 8 electrons, hence O2 molecule has 16 electrons.
- Formation of molecular orbitals (MOs) : Linear combination of two molecular orbitals give two molecular orbitals namely bonding σ or π and antibonding σ* or π*.
- 8 electrons in inner MO, namely σ1s2 σ*1s2 σ2s2 σ*2s2 do not contribute for net chemical bonding. The electronic configuration of O2 molecule is,
O2 : (σ1s2 σ*1s2) (σ2s2 σ*2s2) σ2px2 (π2py2=π2pz2) (π*2py2=π*2pz2)
- [Note : MOs π2py and π2pz as well as π*2py and π*2pz are degenerate]

- Since O2 molecule has 2 unpaired electrons in π*2py2 π*2pz2 orbitals, it is paramagnetic.
- Bond order = (6—2)/2 = 2
- Hence, O2 molecule has a double bond i.e. one sigma and one pi bond.
Formation of F2 molecule with the help of MOT
9F : 1s2 2s2 2p5
The electronic configuration of F2 molecule (18 electrons) is
F2 : (σ1s2 σ*1s2)(σ2s2 σ*2s2) σ2px2 (π2py2=π2pz2) (π*2py2=π*2pz2)

- Bond order of F2 molecule = (10-8)/2= 1
- Since there is no unpaired electron in F2 molecule, it is diamagnetic.
Parameters of covalent bond :
A covalent bond is characterised by different parameters.
The parameters of a covalent bond are : (i) Bond angle (ii) Bond enthalpy (iii) Bond length (iv) Bond order.
(i) Bond angle :
- In a covalent bond, the electrons involved in bond formation are present in orbitals.
- The angle between the orbitals holding the bonding electrons is called the bond angle.

- The value of bond angle gives an idea about the arrangement of orbitals around the central atom and the shape of the molecule.
- Bond angle can be determined experimentally by spectroscopic techniques.
(ii) Bond enthalpy :
- It is the amount of energy (or enthalpy charge) required to break one mole of a particular bond present between two atoms in the gaseous state.
- Bond enthalpy of a diatomic molecule is equal to its dissociation energy.
- Bond enthalpy is a measure of strength of the bond between two atoms.
- Larger the bond dissociation energy stronger is the bond.
- In case of polyatomic molecules, the bond enthalpy is the average of the sum of successive bond dissociation energies.
For example,
H2O(g) → H(g) + OH(g) ΔH1 = 502 kJ mol-1
OH(g) → H(g) + O(g) ΔH2 = 427 kJ mol-1
Hence average bond enthalpy of O—H bond is
ΔH = (502+427)/2 = 464.5 kJ mol-1
(iii).Bond length :
- Bond length implies the equilibrium distance between the nuclei of two covalently bonded atoms in a molecule.
- Bond lengths are measured by X-ray and Electron diffraction techniques.
- Each atom of the bonded pair contributes to the bond length. Bond length depends upon the size of atoms and multiplicity of bonds.
- It increases with increase in size of atom and decreases with increase in multiplicity of bond.
- It is generally measured in picometre (pm) or in Angstrom unit (Å)
(iv) Bond order :
- It is equal to the number of bonds between two atoms in a molecule.
- Isoelectronic molecules and ions have identical bond order, for example H2, F2 have bond order 1 while H2, O2 and N2 have bond order 1, 2 and 3 respectively.
- As bond order increases, bond enthalpy increases and bond length decreases.
Polarity of a covalent bond :
- When a covalent bond is formed between two atoms differing in electronegativity, the electron bond pair is pulled towards more electronegative atom resulting in separation of charges.
- The more electronegative atom acquires a partial negative charge and the less electronegative atom or electropositive atom acquires equal partial positive charge developing a polar covalent bond or a dipole.
- More the bond polarity, stronger is the bond.
- When the difference in electronegativities is about 10%, the covalent bond has about 50% ionic character.
The examples of polar molecules include. HF, HCl etc.
H : F δ+H−Fδ- ….H-F (Polar covalent bond)
Dipole moment :
Definition : Dipole moment (μ) is the product of the magnitude of charge and distance between the centres of +ve and -ve charges.
μ = Q × r
Q : charge ; r : distance of separation.
unit of dipole moment is Debye (D)
1 D = 3.33564 × 10-30 Cm
C : coulomb ; m : meter
Dipole moment being a vector quantity is represented by a small arrow with the tail on the positive centre and head pointing towards the negative centre.
![]()
The crossed arrow above the Lewis structural indicates the direction of the shift of electron density towards the more electronegative atom
Dipole moments of polyatomic molecules :
- Each polar bond in a polyatomic molecule, each polar bond has its own dipole and dipole moment.
- Since dipole moment is a vector quantity, the resultant dipole moment of the molecule is decided by (i) shape of the molecule and (ii) contribution of each dipole moment of a polar bond in the molecule.
- Hence the resultant dipole moment of the polyatomic molecule is the vector sum of the dipole moments of various bonds and lone pairs.
- For example, consider BeF2 molecule. It is a linear molecule ad the bond moments of two Be — F bonds are equal in strength and opposite in direction. Hence the net dipole moment of BeF2 is zero.
![]()
Dipole moment of BF3 molecule :
BF3 is a planar, symmetrical trigonal molecule with bond angle 120°.

Since three B-F polar bonds are oriented at 120° with each other, the sum of any two bond moments is equal and opposite to the third, therefore sum of three B—F dipole moments is zero.
Lone pairs and dipole moment :
- In some molecules, the central atom carries an unshared lone pairs of electrons.
- These lone pairs also contribute to the resultant dipole moment of the molecule. For example, NH3 molecule in which N has one lone pair of electrons.
Examples :
NH3 : In NH3, there are three N—H polar bonds and one lone pair of electrons. Hence NH3 has a net dipole moment.

H2O : In H2O, there are two O—H polar bonds and two lone pairs/of electrons. Hence H2O has a net dipole moment.
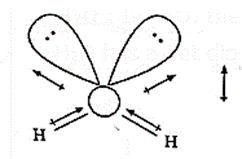
NF3 : NF3 molecule has three N—F polar bonds and one lone pair of electrons. Hence NF3 molecule has a resultant dipole moment.

CH4 : CH4molecule is non—polar and it does not have a lone pair of electrons. Hence it does not have a net dipole moment.

CHCl3 : In CHCl3 molecule there are three C—Cl and one C-H bonds and their dipole moments are not equal. Hence CHCl3 has a resultant dipole moment.

Covalent character of ionic bond :
Several ionic compounds possess partial covalent character and show properties similar to covalent compounds.
To explain the partial covalent character in ionic bonds Fajans put forth the following rules :
- The smaller the size of a cation and larger the size of an anion, greater is covalent character of an ionic compound. For example, LiCl is more covalent than NaCl.
- Greater the charge on cation, more is covalent character of the ionic compound. For example, covalent character decreases as,
3 + − 2 + − + −
AlCl3 > MgCl2 > NaCl
- A cation with outer electronic configuration s2p6d10 possesses greater polarising power than a cation having outer electronic configuration size and same size and charge, since d-electrons have less screening effect than s, p-electrons.
Phenomenon of resonance :
- Many polyatomic molecules can be represented by more than one lewis structures.
- Each structure differs from the other only in position of electrons without changing the position of atoms.
- None of these individual structures explains the properties adequately.
- For example, CO32-

- The actual structure of CO32- is a combination of three Lewis structures and it is called resonance hybrid.
- Resonance signifies that there is more than one possible arrangement of electrons around the atoms in the molecule or more than one Lewis structures. These are also called canonical structures.
Resonance energy :
- Many polyatomic ions and molecules can be represented by different canonical forms and each form has a different energy.
- The energy of resonating structures is different than the energy of the most stable structure or resonance hybrid.
- The difference in energy of the most stable resonating structure or resonance hybrid and different resonating forms is called resonance energy.
Main Page : – Maharashtra Board Class 11th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-4-Structure of Atom – Online Notes
Next Chapter : Chapter-6-Redox Reactions – Online Notes
We reply to valid query.