Notes-Class-10-Mathematics-2-Chapter-6-Trigonometry-Maharashtra Board

Topics to be learn  Trigonometric ratios Trigonometric identities Application of trigonometry

Trigonometric ratios :

Let’s understand :

Consider Δ ABC, where ∠ ABC = 90° and ∠ ACB = θ.

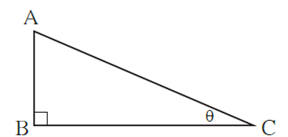
We knew the sine, cosine and tangent ratios of the acute angles of the right angled triangle.

sin θ = \(\frac{\text{Opposite side of angle θ}}{Hypotenuses}=\frac{AB}{AC}\)

cos  θ = \(\frac{\text{Adjacent side of angle θ}}{Hypotenuses}=\frac{BC}{AC}\)

tan θ = \(\frac{\text{Opposite side of angle θ}}{\text{Adjacent side of angle θ}}=\frac{AB}{BC}\)

Relations in ratios are :

(i) \(\frac{sin\,θ}{cos\,θ}\)= tan θ

(ii) sin θ = cos (90 – θ)

(iii) cos θ = sin (90 – θ)

(iv) tan θ × tan (90 – θ) = 1

(v) sin² θ + cos² θ = 1

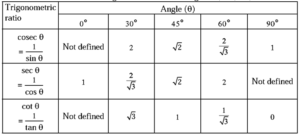
Values of the trigonometric ratios of angles 0°,30°,45°,60° and 90°:

cosec, sec and cot ratios :

Consider Δ ABC, where ∠ ABC = 90° and ∠ ACB = θ.

Here, sin θ = \(\frac{AB}{AC}\) its multiplicative inverse or reciprocal is called ‘cosecant ratio’. Cosecant ratio of θ is written as cosec θ = \(\frac{AC}{AB}{AC}\)

The multiplicative inverses or reciprocals of sine, cosine and tangent ratios are called cosecant, secant and cotangent ratios respectively.

Thus, the definition of the cosecant, secant and cotangent ratios of acute angle θ are as follows :

cosec θ = \(\frac{Hypotenuses}{\text{Opposite side of angle θ}}\)

sec  θ = \(\frac{Hypotenuses}{\text{Adjacent side of angle θ}}\)

cot θ = \(\frac{\text{Adjacent side of angle θ}}{\text{Opposite side of angle θ}}\)

The relation between the trigonometric ratios :

According to the definitions of cosec, sec and cot ratios

(i) sin θ = \(\frac{1}{cosec\,θ}\) ∴ sin θ × cosec θ = 1

(ii) cos θ = \(\frac{1}{sec\,θ}\)  ∴ cos θ × sec θ = 1

(iii) tan θ = \(\frac{1}{cot\,θ}\) ∴ tan θ × cot θ = 1

(iv) tan θ = \(\frac{sin\,θ}{cos\,θ}\)

(v) cot θ = \(\frac{cos\,θ}{sin\,θ}\)

The table of the values of trigonometric ratios of angles 0°,30°,45°,60° and 90° :

Trigonometric identities :

Consider Δ ABC, where ∠ B = 90° and ∠ A = θ.

(i) sin θ = \(\frac{BC}{AC}\) ,  (ii) cos θ = \(\frac{BA}{AC}\)

(iii) tan θ = \(\frac{BC}{AB}\) ,  (iv) cosec θ = \(\frac{AC}{BC}\)

(v) sec θ = \(\frac{BA}{AC}\),  (vi) cot θ = \(\frac{AB}{BC}\)

By Pythagoras therom,

BC² + AB² = AC² . . . . .(1)

Dividing both the sides of (1) by AC²

 \(\frac{BC^2+AB^2}{AC^2}=\frac{AC^2}{AC^2}\)

∴  \(\frac{BC^2}{AC^2}+\frac{AB^2}{AC^2}=1\)

∴ (sin θ)² + (cos θ)² = 1 .... [(sin θ)² is written as sin² θ and (cos θ)² is written as cos² θ.]

sin² θ + cos² θ = 1 .......... (2)

Now dividing both the sides of equation (2) by sin² θ

\(\frac{sin^2\,θ}{sin^2\,θ}+\frac{cos^2\,θ}{sin^2\,θ}=\frac{1}{sin^2\,θ}\)

∴ 1 + cot² θ = cosec² θ .......... (3)

Dividing both the sides of equation (2) by cos² θ

\(\frac{sin^2\,θ}{cos^2\,θ}+\frac{cos^2\,θ}{cos^2\,θ}=\frac{1}{cos^2\,θ}\)

∴ tan² θ + 1 = sec² θ

1 + tan² θ = sec² θ .......... (4)

Relations (2), (3), and (4) are fundamental trigonometric identities.

Application of trigonometry :

Trigonometric ratios can be used in estimating the distance between two inaccessible points or heights of points too high to determine by direct measurement.

For the purpose of computation we shall treat ‘trees’, 'hills‘ or ‘towers’ as ideal vertical objects. We shall represent them in diagram, by segments perpendicular to the ground. Unless there is a mention of observer's height, we shall always regard observers eye to be in the plane of the ground.

Let us study a few related terms.

(i) Line of Vision : If the observer at the location P is looking at an object Q, then the line PQ is called line of vision.

 (ii) Angle of elevation: If an observer at A, observes the point B which is at a level higher than A and AM is the horizontal line, then ∠ BAM is called the angle of elevation.

(iii) Angle of depression : If an observer at A, observes the point C which is at a level lower than A and AM is the horizontal line, the ∠ MAC is called the angle of depression.

• When we see above the horizontal line, the angle formed is the angle of elevation.
• When we see below the horizontal line, the angle formed is the angle of depression.

Example : From the top of a building, an observer is looking at a scooter parked at some distance away, makes an angle of depression of 30°. If the height of the building is 40m, find how far the scooter is from the building. (\(\sqrt{3}\)= 1.73)

Solution:

In the below figure, AB is the building. A scooter is at C which is ‘x’ m away from the building. ‘A’ is the position of the observer.

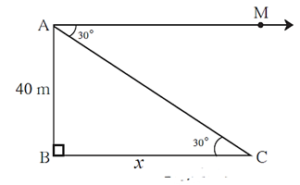
AM is the horizontal line and ∠ MAC is the angle of depression.

∠ MAC and ∠ ACB are alternate angles.

from fig, tan30° = \(\frac{AB}{BC}\)

 \(\frac{1}{\sqrt{3}}=\frac{40}{x}\)

∴ x = 40 × \(\sqrt{3}\) = 40 × 1.73 = 69.20 m.

∴ the scooter is 69.20 m. away from the building.