Electrostatics
Maharashtra Board-Class-11-Science-Physics-Chapter-10
Notes Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Electrostatics : The study of electric charges at rest (called static charges), the forces between them, and the electric field and potential associated with them is known as electrostatics.
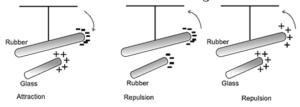
Electrification by friction :
- Many materials may be charged by rubbing them together. An uncharged body is electrically neutral because it has equal amounts of positive and negative charge.
- When two bodies are rubbed against one other, friction transfers some of the loosely bound electrons from one substance to the other; the one that obtains electrons is said to be negatively charged. The second body that loses electrons has a negative charge deficit and is considered to be positively charged.
- Materials can be arranged in an ordered list such that when any two of these are rubbed against each other, the one ahead in the list becomes positively charged while the other becomes negatively charged.
- Examples, (1) fur (2) glass (3) silk (4) human body (5) metals (6) ebonite (7) sealing wax (8) amber (9) resin (10) sulphur. Thus, glass becomes positively charged when rubbed with silk but negatively charged when rubbed with fur.
- That the charges on the two bodies being rubbed are of two different kinds was discovered by Charles Dufay. The terminology, positive and negative (or plus and minus) is due to Benjamin Franklin. Dufay also showed that like charges repel while unlike charges attract each other.
Examples of electrification by friction :
- When we wear or remove our woollen sweater or a synthetic dress on a dry day, electric charges are produced by friction between wool or the fabric and our body. This produces crackling sound and the sweater or dress appears to stick to our body.
- Electric charges develop on clouds due to friction. This results in thunder and lightning under suitable conditions.
- When a glass rod is rubbed with silk, both get charged due to friction.
Electric Charges :
Electrostatic induction :
Electrostatic induction is the process by which an uncharged conductor is brought close to a charged body such that the charge opposing the body's is formed on the nearer side of the conductor and the charge similar to the body's is developed on the far side of the conductor.
Explanation :

- When a charged body is brought near an uncharged conductor, charges are separated to the two ends of the conductor Fig. (a). The charges at the end nearer to the charged body are called bound charges while those at the other end are called free charges.
- When the conductor is grounded, i.e., connected to the earth with a metal wire, electrons flow from the earth to that end and neutralize the free positive charge there. The bound negative charge remains on the conductor, Fig. (b),
- When the grounding is removed, the negative bound charges remain on the conductor, Fig. (c).
- Now, if the charged body is removed, the negative charge on the conductor is distributed, Fig. (d).
Example of use :
When a petrol or a diesel tanker is emptied into a tank, it is grounded. Or A thick chain hangs from a petrol or a diesel tanker and it is in contact with the ground when the tanker is moving. Because, a grounding chain is used to discharge any static charges that may accumulate throughout the voyage so that the charge does not ignite the gasoline when it is loaded or unloaded.
Basic Properties of Electric Charge
Additive Nature of Charge:
Electric charge, like mass, is additive. To compare the additive property of charge with that of mass.
(i) Mass is always positive, while electric charge on a particle is positive or negative. For example, the proton is positively charged and the electron is negatively charged.
(ii) Ignoring binding energy, the total mass of a body is the sum of the masses of its constituents, and is always positive. The total or net charge on a body is the algebraic sum of the charges on its constituent particles. The net charge can be positive, negative or zero.
- It is positive if the number of protons exceeds the number of electrons
- It is negative if the number of protons is less than the number of electrons
- It is zero if the number of protons equals the number of electrons.
(iii) Electric charge, like mass, is a scalar quantity.
Gold Leaf Electroscope:
- This is a classic instrument for detecting presences of electric charge.
- A metal disc is connected to one end of a narrow metal rod and a thin piece of gold leaf is fixed to the other end. The whole of this part of the electroscope is insulted from the body of the instrument. A glass front prevents air draughts but allows to observe the effect of charge on the leaf.
- When a charge is put on the disc at the top it spreads down to the plate and leaf moves away from the plate. This happens because similar charges repel. The more the charge on the disc, more is the separation of the leaf from the plate.
- The leaf can be made to fall again by touching the disc. This is done by earthing the electroscope. An earth terminal prevents the case from accumulating any stray charge.
The electroscope can be charged in two ways :

(a) By contact- a charged rod is brought in contract with the disc and charge is transferred to the electroscope. This method gives the gold leaf the same charge as that on the conductor. This is not a very effective method of charging the electroscope.
(b) By induction- a charged rod is brought close to the disc (not touching it) and the electroscope is earthed. The rod is then removed. This method give the gold leaf opposite charges.
Quantization of Charge:
- The smallest magnitude e of electric charge observable as an isolated charge is that of the charge on an electron or a proton, e ≈6 x 10—19 C.
- The natural unit of negative charge is that on an electron, and a proton has an equal amount of positive charge.
- A macroscopic body that has equal numbers of electrons and protons is electrically neutral. If the body has an excess of electrons, it is negatively charged while deficit of electrons results in a positive charge.
- Thus, electrically charged large scale matter always possesses a charge that is an integral multiple of the natural unit e, i.e., q = ± ne, where n is an integer. Hence, charge is said to be quantized.
Know This :
|
Conservation of Charge:
Law or principle of conservation of charge : In any closed or isolated system, the algebraic sum of all the electric charges is constant, i.e., the net charge cannot be created or destroyed.
Explanation :
- Charges are neither created nor destroyed in any charging process; the two bodies involved in the changing process form a system, and charges are only transferred from one body to another.
- An uncharged body is electrically neutral because its positive and negative charges are equal.
- When two uncharged bodies rub together, one receives electrons from the other, resulting in a net negative charge. The second body, which loses those electrons, has a negative charge deficit and gains a net positive charge of the same size as the first. Their algebraic total of charges remains zero.
- If a charged body is used to charge an uncharged body then the sum of their charges after the charging process is equal to the initial charge on the first body.
- Though charged particles are produced in nature, there is no production of net charge. For example, a gamma ray photon of energy greater than 1.02 MeV, in the presence of a heavy nucleus such as lead, can produce a pair of charged particles — positron (antielectron ≡ positively charged electron) and electron — but there is no net production of charge.
- Conservation of charge is a universal law. Violation of this law has never been observed.
Forces between Charges:
When charged objects are brought close to one another without touching, they feel force. This force can be attractive or repulsive. Like charges repel each other and unlike charges attract each other.
Coulomb’s Law
Coulomb's law: The electrostatic force of attraction or repulsion between two static point charges is directly proportional to the product of the magnitudes of the charges, inversely proportional to the square of their separation and acts along the line joining them.
Coulomb’s law in scalar form :
If q1 and q2 are two point charges separated by a distance r, the magnitude F of the Coulomb force of attraction or repulsion between them is
F ∝ \(\frac{q_1q_2}{r^2}\) ……(1)
∴ F = K\(\frac{q_1q_2}{r^2}\) ……(2)
where K is the constant of proportionality; K depends upon the surrounding medium. For charges in free space, K = \(\frac{1}{4πε_0}\) in SI, where ε0 is the absolute permittivity of free space.
Coulomb force between two point
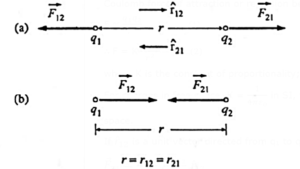
(a) like charges (b) unlike charges
Coulomb’s Law in Vector Form:
If \(\hat{r}_{12}\) is a unit vector directed from q1 to q2, force \(\vec{F}_{21}\) exerted on q2 by q1 is
\(\vec{F}_{21}\) = \(\frac{1}{4πε_0}.\frac{q_1q_2}{r_{12}^2}\,\hat{r}_{12}\) ……(3)
where the charges are taken to be in vacuum and r12 is the distance between the charges.
r12 = \(|\vec{r}_{21}|\) If q1 and q2 are like charges, \(\vec{F}_{21}\) is directed away from q1 and hence, repulsive. If q1 and q2 are unlike charges, \(\vec{F}_{21}\) is towards q1 i.e., attractive.
Similarly, force \(\vec{F}_{12}\) on q1 by q2 is
\(\vec{F}_{12}\) = \(\frac{1}{4πε_0}.\frac{q_1q_2}{r_{12}^2}\,\hat{r}_{21}\)……(4)
where \(\hat{r}_{21}\) is a unit vector directed from q2 to q1;
\(\hat{r}_{21}\) = \(-\hat{r}_{12}\) and \(\vec{F}_{12}\) = \(-\vec{F}_{21}\) , i.e., \(\vec{F}_{12}\) and \(\vec{F}_{21}\) are an action-reaction pair.
r21 = \(|\vec{r}_{21}|\), r12 = \(|\vec{r}_{12}|\) and r21 = r12
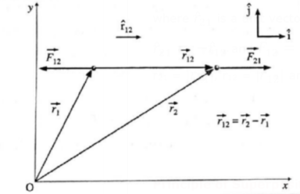
Coulomb's law in vector form : q1 and q2 are like charges
If the charges are kept in a medium (such as mica) of absolute permittivity ε, ε0 is replaced by ε so that Eqs. (3) and (4) become, respectively,
\(\vec{F}_{21}\) = \(\frac{1}{4πε}.\frac{q_1q_2}{r_{12}^2}\,\hat{r}_{12}\) …(5)
and
\(\vec{F}_{12}\) = \(\frac{1}{4πε}.\frac{q_1q_2}{r_{12}^2}\,\hat{r}_{21}\) …..(6)
Know This :
|
Relative Permittivity or Dielectric Constant :
When the charges are kept in a material medium, such as water, mica or parafined paper, the medium affects the force between the charges. The force between the two charges placed in a medium may be written as,
Fmed = \(\frac{1}{4πε}(\frac{q_1q_2}{r^2})\) …..(1)
where ε is called the absolute permittivity of the medium. The force between the same two charges placed in free space or vacuum at distance r is given by,
Fvac = \(\frac{1}{4πε_0}(\frac{q_1q_2}{r^2})\) …..(2)
Dividing Eq. (1) by (2)
\(\frac{F_{med}}{F_{vac}}\) = \(\frac{\frac{1}{4πε}(\frac{q_1q_2}{r^2})}{\frac{1}{4πε_0}(\frac{q_1q_2}{r^2})}\) = \(\frac{ε}{ε_0}\)
The ratio ε/ε0 is the relative permittivity or dielectric constant of the medium and is denoted by εr or K.
K or εr = \(\frac{ε}{ε_0}\) = \(\frac{F_{med}}{F_{vac}}\)
- The relative permittivity (εr) ( ≡ dielectric constant) of a medium is the ratio of the absolute permittivity of the medium (ε) to the absolute permittivity of free space (≡ vacuum (ε0)).
- εr is the ratio of the force between two point charges placed a certain distance apart in free space or vacuum to the force between the same two point charges when placed at the same distance in the given medium. εr is a dimensionless quantity.
- εr is also called specific inductive capacity.
SI unit and dimensions of absolute permittivity :
(1) In the usual notation, F = \(\frac{1}{4πε}(\frac{q_1q_2}{r^2})\)
∴ ε = \(\frac{q_1q_2}{4πFr^2}\)
The SI unit of charge is the coulomb, that of force is the newton, and that of distance is the metre.
Hence the SI unit of absolute permittivity ε is \(\frac{coulomb^2}{newton.metre^2}\) usually written as C2/N.m2.
(2) We have [ε] = \(\frac{[q_1q_2]}{[F][r^2]}\) as 4π is a pure number.
Now, [q] = [IT], [F] =[MLT—2] and [r] = [L]
∴ [ε] = \(\frac{[I^2T^2]}{[MLT^{-2}][L^2]}\) = [M—1L—3T4I2]
Thus, the dimensions of ε are —1 in mass, —3 in length, 4 in time and 2 in current I.
Definition of Unit Charge from the Coulomb’s Law::
- The SI unit of charge is the coulomb (C).
- Using Coulomb's law, it is defined as follows : One coulomb is the amount of charge, which placed at a distance of one metre from another charge of the same magnitude in vacuum, experiences a force of 9.0 x 109
| Know This :
Comparison of gravitational and electrostatic forces: Similarities :
Differences :
|
Principle of Superposition :
The electrostatic force between two point charges is given by Coulomb's law, irrespective of the presence of other similar point charges in the vicinity.
Principle of superposition of forces : The resultant, i.e., the net force on a point charge due to its interaction with other point charges in its vicinity the vector sum of the forces simultaneously exerted on it by the individual charges at a given instant.
Consider, for example, two point charges q1 and q2 in free space exerting forces simultaneously on a third point charge q3 (see Fig.).
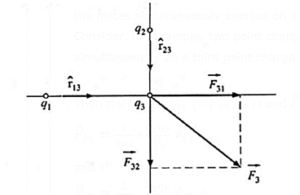
Then the forces \(\vec{F}_{31}\) (≡ \(\vec{F}\) on 3 by 1) and \(\vec{F}_{32}\) ((≡ \(\vec{F}\) on 3 by 2) are
\(\vec{F}_{31}\) = \(\frac{1}{4πε_0}.\frac{q_1q_3}{r_{13}^2}\,\hat{r}_{13}\)
and
\(\vec{F}_{32}\) = \(\frac{1}{4πε_0}.\frac{q_2q_3}{r_{23}^2}\,\hat{r}_{23}\)
where r13 is the distance between q1 and q3, r23 is that between q2 and q3,
\(\hat{r}_{13}\) is a unit vector directed from q1 to q3, \(\hat{r}_{23}\) is a unit vector directed from q2 to q3.
The resultant force on q3 is \(\vec{F}_3\)
\(\vec{F}_3 = \vec{F}_{31} + \vec{F}_{32}\)
= \(\frac{1}{4πε_0}[\frac{q_1q_3}{r_{13}^2}\hat{r}_{13}+\frac{q_2q_3}{r_{23}^2}\hat{r}_{23}]\)
This can be extended to any number of point charges.
In general, if there are N charges,
\(\vec{F}_1 = \vec{F}_{12} + \vec{F}_{13}+\vec{F}_{14}+ ....+\vec{F}_{1N}\) is the resultant force on q1.
and is the resultant force on q1.
and
\(\vec{F}_i = \sum_{j=1}^{N}\vec{F}_{ij}\) .... j ≠ i
= \(\frac{1}{4πε_0} \sum_{j=1}^{N}\frac{q_iq_j}{r_{ij}^2}\hat{r}_{ij}\)
is the resultant force on qi
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 9: Optics – Online Notes
Next Chapter : Chapter 11: Electric Current Through Conductors – Online Notes
We reply to valid query.