Notes-Part-1-Class-12-Physics-Chapter-5-Oscillations-MSBSHSE

Spring-and-block oscillator :

Consider a spring-and-block oscillator as shown in Fig. in which the block slides on a frictionless horizontal surface. The spring has a relaxed length when the block is at rest at the position B, Fig.(b).  The block is then displaced to A by an amount x measured from the equilibrium position B, Fig.(a). Upon releasing, the unbalanced force \(\vec{F}\) = \(−k\vec{x}\) toward left accelerates the block and its speed increases. As x gets smaller, |\(\vec{F}\) | and the acceleration decrease proportionately.

k is the elastic constant of the spring called the force constant or spring constant.

At the instant the block passes through the point B, |F | = 0 because x = 0; although there is no acceleration, the speed is maximum.

As soon as the block passes B going to the left, the force on the block and its acceleration increases to the right, because the spring is now compressed.

Eventually, the block is brought to rest momentarily at the point C. Then on, the subsequent motion is the same as the motion from A to C, with all directions reversed.

The acceleration of the block is a = F/m = \(−\frac{k}{m}x\) , where m is the mass of the block. This shows that the acceleration is also proportional to the displacement and its direction is opposite to that of the displacement, i.e., the force and acceleration are both directed towards the mean or equilibrium position. The motion repeats causing the block to oscillate about equilibrium or mean position O. This oscillatory motion along a straight path is called linear simple harmonic motion (SHM).

The points A and C are called the extreme positions or the turning points of the motion. One oscillation is a complete to-and-fro motion of the oscillating body (block, in this case) along its path (the motion from B to A, A to C and C to B), i.e., two consecutive passages of the body through the point B in the same direction.

Differential Equation of S.H.M. : When a particle performs linear SHM, the force acting on the particle is always directed towards the mean position. The magnitude of the force is directly proportional to the magnitude of the displacement of the particle from the mean position. Thus, if F is the force acting on the particle when its displacement from the mean position is x,

F = − kx

According to Newton’s second law of motion,

F = ma   ∴ ma = − kx   ….. (1)

The velocity of the particle is, v = dx/dt

and its acceleration, a = dv/dt = d²x/dt²

Substituting it in Eq. (1), we get

\(m\frac{d^2x}{dt^2}\) = − kx  

\(∴ \frac{d^2x}{dt^2}+\frac{k}{m}x=0\)  ….. (2)

Substituting k/m = ω², where ω is the angular frequency,

\(∴ \frac{d^2x}{dt^2}+ω^2x=0\)   This is the differential equation of linear S.H.M.

Acceleration (a), Velocity (v) and Displacement (x) of S.H.M. :

The differential equation of linear SHM is\(\frac{\vec{d^2x}}{dt^2}+ω^2\vec{x}=0\) 

where m = mass of the particle performing SHM

\(\frac{d^2x}{dt^2}\) = acceleration of the particle when its displacement from the mean position is x and k = force constant. For linear motion, we can write the differential equation in scalar form \(\frac{d^2x}{dt^2}+ω^2x=0\) 

 Let k/m = ω² , a constant.

∴ acceerat1on, a = d²x/dt² = −ω²x …....(1)

The minus sign shows that the acceleration and the displacement have opposite directions. Writing

v = dx/dt  as the velocity of the particle.

Hence, Eq. (1) can be written as

\(a=\frac{d^2x}{dt^2}=\frac{dv}{dt}=\frac{dv}{dx}⋅\frac{dx}{dt}=\frac{dv}{dx}⋅v =v⋅\frac{dv}{dx}\)= −ω²x

∴ v.dv = −ω²x  dx

Integrating this expression, we get,

\(\frac{v^2}{2}=−\frac{ω^2x^2}{2}+C\)

where the constant of integration C is found from a boundary condition.

At an extreme position (a turning point of the motion), the velocity of the particle is zero. Thus, v = 0 when x = ± A, where A is the amplitude.

∴ 0 =(−\frac{ω^2A^2}{2}+C\)

∴ C =(\frac{ω^2A^2}{2}\)

∴\(\frac{v^2}{2}=−\frac{ω^2x^2}{2}+\frac{ω^2A^2}{2}\)

∴ v² = ω²(A² - x²)

∴ v = ±ω\(\sqrt{A^2-x^2}\)    ….. (2)

This equation gives the velocity of the particle in terms of the displacement, x. The velocity towards right is taken to be positive and that towards left as negative.

Since, v = dx/dt, we can write Eq. (2) as follows :

\(\frac{dx}{dt}\)= ω\(\sqrt{A^2-x^2}\)  ..... (considering only the plus sign)

∴ \(\frac{dx}{\sqrt{A^2-x^2}}\)= ωdt

Integrating this expression, we get,

sin⁻¹(x/A) = ωt + α  …… (3)

where the constant of integration, α, is found from the initial conditions, i.e., the displacement and the velocity of the particle at time t = 0.

From Eq. (3), we have

x/A = sin(ωt + a)

∴ Displacement as a function of time is,

x = A sin(ωt + a)

Expressions for the displacement when the particle starts from (i) the mean position (ii) an extreme position :

The displacement of a particle performing linear SHM is a specified distance of the particle from the mean position in a specified direction along its path. The general expression for the displacement is

x = A sin(ωt + α) ….. (1)

where A and w are respectively the amplitude or maximum displacement and the angular frequency of the motion, and a is the initial phase.

\(v=\frac{dx}{dt}=\frac{d}{dt}[A sin(ωt + α)]\)

∴ ωt + α = sin^-1(x/A) ….. (2)

Case (i)  When the particle starts from the mean position, x = 0 at t= 0. Then, from Eq.(2),

α = sin⁻¹0 = 0 or π  …..(3)

Substituting for α into Eq. (1),

x = A sin ωt   ... for α = 0

and   x= − A sin ωt    ....for α = π

∴ x = ± A sin ωt  ….(4)

where the plus sign is taken if the particle's initial velocity is to the right, while the minus sign is taken when the initial velocity is to the left.

Case (ii) If the particle starts S.H.M. from the extreme position :

x= ± A at t = 0  when the particle starts from the right or left extreme position, respectively.

Then, from Eq. (2),

α = sin^-11 = π/2  or  α = sin^-1(-1) = 3π/2  ……..(5)

Substituting for α into Eq. (1),

x = A sin(ωt + π/2) = A cos ωt   …for α = π/2

x = A sin(ωt + 3π/2) = − A cos ωt  …..for α = 3π/2

∴ x = ± A cos ωt  ……..(6)

where the plus sign is taken when the particle starts from the positive extreme, while the minus sign is taken when the particle starts from the negative extreme.

Obtaining expression for (a) velocity (b) acceleration in SHM, by using the differential equation of linear SHM :

The general expression for the displacement of a particle in SHM at time t is

x = A sin(ωt + α) ….. (1)

where A and ω is a constant in a particular case and α is the initial phase.

The velocity of the particle is 

\(v=\frac{dx}{dt}=\frac{d}{dt}[A sin(ωt + α)]\)

= ωA cos(ωt + α)

= \(ωA\sqrt{1-sin^2(ωt + α)}\)

From Eq. (1), sin(ωt + α) = x/A

\(v=ωA\sqrt{1-\frac{x^2}{A^2}}\)

∴ \(v=ω\sqrt{A^2-x^2}\)  …… (2)

Equation (2) gives the velocity as a function of x

The acceleration of the particle is

a= \(\frac{dv}{dt}=\frac{d}{dt}\)[Aω cos(ωt + α)]

∴ a = − ω²A sin(ωt + α)

But from Eq. (1),  A sin(ωt + α) = x

∴ a = − ω²x  ……. (3)

Equation (3) gives the acceleration as a function of x. The minus sign shows that the direction of the acceleration is opposite to that of the displacement.

Extreme values of  velocity (v) and acceleration (a):

Velocity: According to Eq. (2) from above the magnitude of velocity of the particle performing S.H.M. is

v = ±\(ω\sqrt{A^2−x^2}\)

At the mean position, x = 0,  ∴ v_max = ωA

Thus, the velocity of the particle in S.H.M. is maximum at the mean position.

At the extreme position,  x = ± A , ∴ v_min = 0

Thus, the velocity of the particle in S.H.M. is minimum at the extreme positions.

Acceleration: The magnitude of the acceleration of a particle performing SHM is

a =  ω²x   ……(1)

where w is a constant related to the system.

From Eq. (1), the acceleration has a maximum value a_max when displacement x is maximum, |x| =A, i.e., the particle is at the extreme positions.

∴ a_max = ω²A

Also from Eq. (1), the acceleration has a minimum value a_min when x is minimum, x = 0, i.e., the particle is at the mean position.

∴ a_min = 0

Expressions for the period of SHM in terms of (1) angular frequency (2) force constant (3) acceleration. :

The general expression for the displacement (x) of a particle performing SHM is

x = A sin(ωt + α)

(1) Let T be the period of the SHM and x₁ the displacement after a further time interval T.

Then

x₁ = A sin[ω(t+T) + α]

 = A sin(ωt + ωT + α)

= A sin(ωt + α + ωT)

Since T ≠ 0 , for x₁ to be equal to x, we must have (ωT)_min = 2π

Hence, the period (T) of SHM is T =  2π/ω

This is the expression for the period in terms of the constant ω, the angular frequency.

(2) If m is the mass of the particle and k is the force constant, ω = \(\sqrt{\frac{k}{m}}\)

∴ T = 2π/ω = \(\frac{2π}{\sqrt{k/m}}\)

This is the expression for the period in terms of the force constant.

(3) The acceleration of a particle performing SHM has a magnitude

a = ω²x

∴ ω = \(\sqrt{a/x}\) = \(\sqrt{\text{acceeration per unit displacement}}\)

∴ T = 2π/ω = \(\frac{2π}{\sqrt{\text{acceeration per unit displacement}}}\)

Frequency of an SHM vary with (i) the force constant k (ii) the mass of the particle performing SHM :

The frequency of a particle of mass m performing SHM is

η = 1/T = \(\frac{1}{2π}\sqrt{k/m}\)

(i) ∴ η  ∝ \(\sqrt{k}\)

Thus, the frequency of an SHM is directly proportional to the square root of the force constant of the motion.

(ii) ∴ η  ∝ \(\sqrt{1/m}\)

Thus, the frequency of an SHM is inversely proportional to the square root of the mass of the particle performing SHM.

Parallel combination (Figure B): In such a combination, all the springs are connected between same two points, one of them is the support and at the other end, the stretching force F is applied at a suitable point.

Irrespective of their spring constants, each spring will now have the same extension x.

The springs now share the force such that in the equilibrium position, the total restoring force is equal and opposite to the stretching force F.

Let F₁ = k₁x, F₂ = k₂x………. be the individual restoring forces.

If k_P is the effective spring constant, a single spring of this spring constant will be stretched by the same extension x, by the same stretching force F.

∴ F = k_Px  = F₁+F₂+ ….. = k₁x+ k₂x +….

∴ k_P = k₁ + k₂ +…. = \(\sum k_i\)

For N such identical massless springs of spring constant k each, in parallel, k_P = Nk

Linear SHM is the projection of a uniform circular motion on its diameter :

Consider a particle which moves anticlockwise around a circular path of radius r with a constant angular speed w (Fig).

Let the path lie in the x-y plane with the centre at the origin O. The instantaneous position P of the particle is called the reference point and the circle in which the particle moves as the reference circle.

The perpendicular projection of P onto the y-axis is Q. Then, as the particle travels around the circle, Q moves to-and-fro along the y-axis. Line OP makes an angle a with the x-axis at t= 0. At time t, this angle becomes θ = ωt + α.

The projection Q of the reference point is described by the y-coordinate,

y = OQ = OP sin ∠OPQ, Since  ∠OPQ = ωt + α.

y = r sin(ωt + α.)

which is the equation of a linear SHM of amplitude A. The angular frequency w of a linear SHM can thus be understood as the angular velocity of the reference particle.

Projection of velocity: The tangential velocity of the reference particle is

v = ωr. Its y-component at time t is‘

v_y = ωr sin (90°− θ) = ωr cos θ

v_y = ωr cos (ωt + α)

Projection of acceleration: The centripetal acceleration of the reference particle is a_r = ω²r , so that its y-component at time t is

a_x = a_r sin ∠OPQ

∴ a_x = − ω²r sin (ωt + α) = − ω²y

Special cases: [θ= (ωt + α)]

• Phase θ = 0 indicates that the particle is at the mean position, moving to the positive, during the beginning of the first oscillation. Phase angle 360⁰ or 2π rad is the beginning of the second oscillation, and so on for the successive oscillations.
• Phase θ = 180⁰ or π rad indicates that during its first oscillation, the particle is at the mean position and moving to the negative.

• Similar state in the second oscillation will have phase θ = (360 + 180)⁰ or (2π + π) rad, and so on for the successive oscillations.

• Phase θ = 90⁰ or π/2 indicates that the particle is at the positive extreme position during first oscillation. For the second oscillation it will be θ = (360 + 90)⁰ or (2π + π/2) rad, and so on for the successive oscillations.
• Phase θ = 270⁰ or 3π/2 rad indicates that the particle is at the negative extreme position during the first oscillation. For the second oscillation it will be θ = (360 + 270)⁰ or (2π + 3π/2) rad, and so on for the successive oscillations.

(a) Particle executing S.H.M., starting from mean position, towards positive:

Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where w is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are

x = A sin ωt = A sin\(\frac{2π}{T}t\)     (...ω = 2π/T)

v = dx/dt = ωA cosωt = ωA cos\(\frac{2π}{T}t\) 

a = dv/dt = − ω²A sin ωt = − ω²A sin\(\frac{2π}{T}t\) 

as the initial phase α = 0

Using these expressions, the values of x, v and α at the end of every quarter of a period, starting from t = 0, are tabulated below.

Using the values in the table we can plot graphs of displacement, velocity and acceleration with time (see Fig below).

Fig-Graphs of displacement, velocity and acceleration with time for a particle in SHM starting from the mean position

Conclusions from the graphs:

• Displacement, velocity and acceleration of S.H.M. are periodic functions of time.
• Displacement time curve and acceleration time curves are sine curves and velocity time curve is a cosine curve.
• There is phase difference of π/2 radian between displacement and velocity.
• There is phase difference of π/2 radian between velocity and acceleration.
• There is phase difference of π radian between displacement and acceleration.
• Shapes of all the curves get repeated after 2π radian or after a time T.

• The phase differences are independent of the initial phase

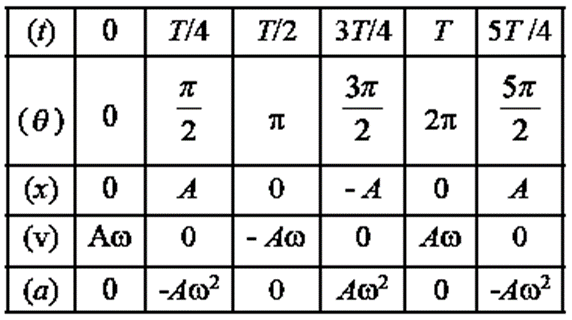
(b) Particle performing S.H.M., starting from the positive extreme position :

Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where w is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are (α = π/2)

x = A sin (ωt+π/2) = A cos ωt = A cos    (ω = 2π/T)

v = dx/dt = −ωA sin ωt = −ωA sin

a = dv/dt = −ω²A cos ωt = −ω²A cos

Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.

[…θ= (ωt + α), at ωt=0, θ=(0+π/2)= π/2 …….]

Using the values in the table we can plot graphs of displacement, velocity and acceleration with time (see Fig below).

Conclusions :

• The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x—t and a—t graphs are cosine curves; the v—t graph is sine curve.
• There is a phase difference of π/2 radians between x and v, and between v and a.
• There is a phase difference of π radians between x and a.
• The phase differences are independent of the initial phase

Explanations :  

(1) v—t graph : It is a sine curve, i.e., the velocity is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π/2 rad between a and v.

v is minimum (equal to zero) at the extreme positions (i.e., at x=±A) and v is maximum ( = ±ωA) at the mean position (x = 0).

(2) a—-t graph : It is a cosine curve, i.e., the acceleration is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of p rad between v and a.

a is minimum (equal to zero) at the mean position (x = 0) and a is maximum (=±ω²A) at the extreme positions (x = ± A).

Composition of two S.H.M.s having same period and along the same path:

Consider a particle subjected simultaneously to two S.H.M.s having the same period and along same path (let it be along the x-axis), but of different amplitudes and initial phases. The resultant displacement at any instant is equal to the vector sum of its displacements due to both the S.H.M.s at that instant.

Equations of displacement of the two S.H.M.s along same straight line (x-axis) are

x₁ = A₁ sin (ωt + α) and x₂ = A₂ sin (ωt + β),

where A₁ and A₂ are the amplitudes, and αand β are the initial phases of the two SHMs.

According to the principle of superposition, the displacement of the particle at any instant t is the algebraic sum _x = x₁ + x₂.

 x = A₁ sin (ωt + α) + A₂ sin (ωt + β)),

= A₁ sin ωt cos α + A₁ cos ωt sin α + A₂ sin ωt cos β + A₂ cos ωt sin β

= (A₁ cos α + A₂ cos β) sin ωt + (A₁ sin α + A₂ sin β) cos ωt

Let A₁ cos α+ A₂ cos β = R cos δ……(1)

And A₁ sin α + A₂ sin β = R sin δ ...(2)

  x = R cos δ sin ωt + R sin δ cos ωt

 x = R sin (ω + δ) …..(3)

Equation (3), which gives the displacement of the particle, shows that the resultant motion is also simple harmonic, along the same path as the SHMs superposed, with the same mean position, and amplitude R and initial phase d but having the same period as the individual SHMs.

Amplitude R of the resultant motion : The resultant amplitude R is found by squaring and adding Eqs. (1) and (2).

R² = R² cos²δ + R² sin²δ

= (A₁ cos α + A₂ cos β)² + (A₁ sin α + A₂ sin β)²

= A₁² cos²α + A₂² cos² β +2A₁A₂ cos α cos β +A₁² sin²α +A₂² sin²β +2A₁A₂ sin α sin β

= A₁² (cos²α + sin²α) + A₂²(cos² β + sin² β) + 2A₁A₂(cos α cos β + sin α sin β)

∴ R² = A₁² + A₂² + 2A₁A₂(cos α − β)

∴ R = \(\sqrt{A_1^2+A_2^2+2A_1A_2(cosα − β)}\)  ……(4)

Initial phase d of the resultant motion : The initial phase of the resultant motion is found by dividing Eq. (2) by Eq. (1).

\(\frac{Rsinδ}{Rsinδ} = tanδ = \frac{A_1sinα+A_2sinβ}{A_1cosα+A_2cosβ}\)

δ = \(tan^{-1}(\frac{A_1sinα+A_2sinβ}{A_1cosα+A_2cosβ})\) ……..(5)

Now, consider Eq. (4) for R.

Case (1) : Phase difference, or α − β = 0°

∴ cos (α − β) = 1

∴ R = \(\sqrt{A_1^2+A_2^2+2A_1A_2}\) =  A₁ + A₂

Case (2) : Phase difference, α − β =π/3 rad

∴ cos (α − β) = 1/2

∴ R = \(\sqrt{A_1^2+A_2^2+A_1A_2}\)

Case (3) : Phase difference, α − β =π/2 rad

∴ cos (α − β) = 0

∴ R = \(\sqrt{A_1^2+A_2^2}\)

∴Case (4) : Phase difference, α − β =π rad

∴ cos (α − β) = −1

∴ R = \(\sqrt{A_1^2+A_2^2-2A_1A_2}\)

∴ R = |A₁ − A₂|

• Since the displacements due to the superposed linear SHMs are along the same path, their vector sum can be replaced by the algebraic sum.
• To determine d uniquely, we need to know both sin d and cos d.