Notes
| Topics to be learn :
Methods of solving Linear Equations in Two Variables
Equations that can be transformed in Linear Equations in Two Variables. Application of Simultaneous Equations. |
Linear Equation in Two Variables :
An equation in two variables with the degree of the variables 1, is called a linear equation in two variables.
Example : (i) 6x + 2y = 12 (ii) 5x - 5y = 2 are linear equations in two variables x and y. The degree of the variables x and y is 1.
| Note :
(1) \(\frac{2}{x}+\frac{2}{y}= 7\) is not a linear equation in two variables, because the degree of the variables x and y is —1. But by proper substitution, it can be converted into linear equation in two variables. Substituting m for \(\frac{1}{x}\) and n for \(\frac{1}{y}\) the given equation becomes, 3m + 2n = 7, which is a linear equation. (2) 3x2 + 2y2 = 10 is not a linear equation in two variables, because the degree of the variables x and y is 2. Such equation cannot be converted into linear equation. |
General Form of a Linear Equation in Two Variables :
ax+by+c=0 is the general form of a linear equation in two variables. Here, a, b and c are real numbers.
e.g. 3x + 5y - 15 = 0 is the general form of the equation 3x + 5y = 15.
[If a = 0 or b = 0, then the equation is a linear one in one variable]
Activity : Through this activity, we can recognize linear equations in two variables.
| Sr. | Equation | Is the equation a linear equation in 2 variables ? |
| 1 | 4m + 3n = 12 | Yes- (Two variables each with degree 1) |
| 2 | 3x2 - 7y = 13 | No- (The degree variable x is 2) |
| 3 | \sqrt{2}x-\sqrt{5}y = 16 | Yes- (Two variables each with degree 1) |
| 4 | 0x + 6y - 3 = 0 | No-(Only one variable y) |
| 5 | 0.3x + 0y -36 = 0 | No-(Only one variable x) |
| 6 | \(\frac{4}{x}+\frac{5}{y}= 4\) | No-(The degree of variables is – 1)
[This can be converted into a linear equation by making proper substitutions.] |
| 7 | 4xy - 5y - 8 = 0 | No-(The degree of xy is 2) |
Simultaneous linear equations : If Two linear equations involving two variables taken together form a system of simultaneous linear equations.
Example
- 7x - 4y = 5; 3x+3y = 9
- 4s + 3t = 12; 4s - 5t = 2
- 5x - 3y = 8; 3x + y = 2
Methods of Solving Simultaneous Equations :
(1) The method of elimination by equating the coefficients
(2) The method of elimination by substitution
(3) By graphical method
(4) By Cramer’s rule (Determinant method)
Note : While solving an equation, the solution of a linear equation is not affected when
|
Text Book Example.
Solve : 3x + 2y = 29; 5 x - y = 18
3 x + 2 y = 29. . . (1) and 5 x - y = 18 . . . (2) Solving simultaneous equations by the method of elimination Multiplying equation (2) by 2. 5x × [2] – y × [2] = 18 ´ [2] ∴ 10 x – 2y = [36] …..(3) Adding equations (1) and (3) \(\begin{array}{rrrrrrr} ∴ x = 5 .... (Dividing both the sides by 13) Substituting x = 5 in equation (1), 3x + 2y = 29 3 × [5] + 2y = 29 [15] + 2y = 29 2y = 29 – [15] ∴ 2y = [14] ∴ y = 7 (x, y) = ([5],[7]) is the solution
& 3x & + & 2y & = & 29 &\text{…..(1)}\\
+ & & & & & & \\
& [10x] & - & [2y] & = & [36] &\text{…..(3)} \\ \hline
& 13x & & & = & [65] & \\
\end{array}\)
Graph of 3 Linear Equation in Two Variables :
- The graph Of 3 linear equation in two variables is a line.
- The ordered pair which satisfies the equation is a solution of that equation.
- The ordered pair represents a point on that line.
Steps to follow for drawing a Graph of Linear Equation in two variables :
- Choose at least three to four convenient values of x and find the corresponding values of y satisfying the given equation.
- Write the values of x and y in tabular form. -
- Draw X-axis, Y-axis on graph paper and plot the points.
- See that all the points lie on a line.
- The coordinates of the point of intersection of the two lines is the solution of the given equations.
| Note : Two points are sufficient to represent a line, but if co-ordinates of one of the two points are wrong then you will not get a correct line.
If you plot three points and if they are non collinear then it is understood that one of the points is wrongly plotted. But it is not easy to identify the incorrect point. If we plot four points, it is almost certain that three of them will be collinear. |
Activity (I) (Text Book) :
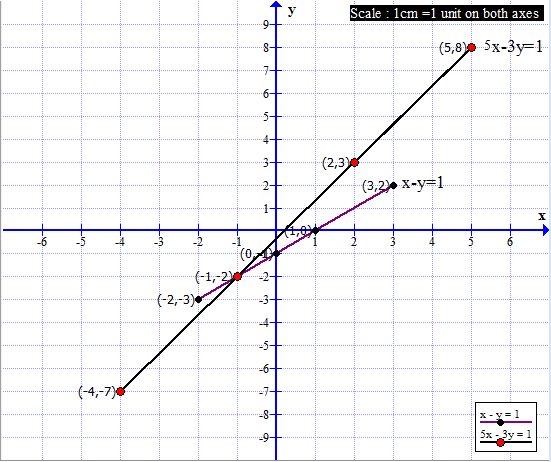
Q. Solve the following simultaneous equations by graphical method.
- Complete the following tables to get ordered pairs.
x - y = 1
|
5x - 3y = 1
|
- Plot the above ordered pairs on the same co-ordinate plane.
- Draw graphs of the equations.
- Note the co-ordinates of the point of intersection of the two graphs.
- Write solution of these equations.
The coordinates of the point of intersection are ( – 1, – 2). (x, y) = ( – 1, – 2) is the solution.
x – y = 1
x
0
1
3
–2
y
–1
0
2
-3
(x, y)
(0,–1)
(1,0)
(3,2)
(–2,–3)
5x – 3y = 1
x
2
5
–1
–4
y
3
8
–2
–7
(x, y)
(2,3)
(5,8)
(–1,–2)
(–4,–7)
Activity II (Text Book) :
Solve the above equations by method of elimination. Check your solution with the solution obtained by graphical method.
x – y =1 ……(1) 5x – 3y = 1 …….(2) Multiplying equation (1) by 3, 3x – 3y = 3 ……..(3) Subtracting equation (3) from equation (2), \(\begin{array}{rrrrrrr} ∴ x = –1 ….(Dividing both the sides by 2) Substituting x = -1 in equation (1), –1 – y = 1 –y = 1 + 1; ∴ –y = 2 ∴ y = –2 (–1, –2) is the solution of the given equations The solution in both the methods is the same.
& 5x & - & 3y & = & 1 &\text{…..(2)}\\
- & & & & & & \\
&3x & - & 3y & = & 3 &\text{…..(3)} \\
-& & +& & &-& \\ \hline
& 2x & & & = & -2 & \\
\end{array}\)
|
Let’s think (Textbook) The following table contains the values of x and y coordinates for ordered pairs to draw the graph of 5x – 3y = 1.
(1) Is it easy to plot these points? (2) Which precaution is to be taken to find ordered pairs so that plotting of points becomes easy?
(1) It is difficult to plot these points except (–1/5, 0). The others have 3 in the denominators. These numbers are non-terminating recurring decimals. Hence, their values are to be taken approximately. We can’t mark points accurately on the graph. (2) The values of x and y should be selected in such a way that the coordinates are integers and not fractional numbers having denominators other than 2 or 5.
|
Let’s discuss. (Text Book)
To solve simultaneous equations x + 2y = 4 ; 3x + 6y = 12 graphically, following are the ordered pairs.
x + 2y = 4
| x | –2 | 0 | 2 |
| y | 3 | 2 | 1 |
| (x,y) | (–2,3) | (0,2) | (1,2) |
3x + 6y = 12
| x | –4 | 1 | 8 |
| y | 4 | 1.5 | –2 |
| (x,y) | (–4,4) | (1,1.5) | (8,–2) |
Plotting the above ordered pairs, graph is drawn. Observe it and find answers of the following questions.
(1) Are the graphs of both the equations different or same ?
(2) What are the solutions of the two equations x + 2y = 4 and 3x + 6y = 12 ? How many solutions are possible ?
(3) What are the relations between coefficients of x, coefficients of y and constant terms in both the equations ?
(4) What conclusion can you draw when two equations are given but the graph is only one line ?
(1) The graphs of both the equations are same. (2) The solutions of the given equations are ( –4, 4), ( –2, 3), (0, 2), (1, 1.5), (2, 1), (8, –2). Infinite solutions are possible. (3) The ratio of the coefficients of x = \(\frac {a_1}{a_2}\) = \(\frac 13\) ….(1) The ratio of the coefficients of y = \(\frac {b_1}{b_2}\) = \(\frac 26\) = \(\frac 13\) …..(2) The ratio of the constants = \(\frac {c_1}{c_2}\) = \(\frac{4}{12}\) = \(\frac 13\) ….(3) All these ratios are the same. (4) If a1x + b1y = c1 and a2x + b2y = c2 are the given equations and if \(\frac {a_1}{a_2}\) = \(\frac {b_1}{b_2}\) = \(\frac {c_1}{c_2}\) , then the graph of the given two equations is only one line, having infinite solutions.
Let us consider another example (Text Book) :
Draw graphs of x - 2y = 4, 2x - 4y = 12 on the same co-ordinate plane.
Observe it. Think of the relation between the coefficients of x, coefficients of y and the constant terms and draw the inference.
x - 2y = 4 \ y = x-4/2 2x - 4y = 12 \ y= 2x-12/4 The graphs of the given equations are parallel lines. The ratio of the coefficients of Considering the given equations as a1x + b1y = c1 and a2x + b2y = c2, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}≠\frac{c_1}{c_2}\) Inference : If \(\frac{a_1}{a_2}=\frac{b_1}{b_2}≠\frac{c_1}{c_2}\) then the graphs of the given two equations are parallel lines having no solution.
x
–2
0
2
4
y
–3
–2
–1
0
(x,y)
(–2,–3)
(0,–2)
(2,–1)
0
x
–4
–2
0
4
y
5
–4
–3
–1
(x,y)
(–4,5)
(–2,-4)
(0,–3)
(4,–1)
Determinant : \(\begin{vmatrix} a &b \\ c& d \end{vmatrix}\) is a determinant of four numbers a, b, c, d.
(a, b), (c, d) are rows and \(\begin{pmatrix} a\\c \end{pmatrix},\begin{pmatrix} b\\d \end{pmatrix}\) are columns.
The degree of this determinant is 2, because there are 2 elements in each column and 2 elements in each row. The determinant represent a number which is (ad-bc).
= (ad-bc).
ad - bc is the value of the determinant \(\begin{vmatrix} a &b \\ c& d \end{vmatrix}\)
Determinants are usually represented with capital letters A, B, C, etc.
Determinant Method (Cramer’s Rule) :
Determinant method of solving simultaneous equations was first given by a Swiss mathematician Gabriel Cramer. So, it is also known as Cramer’s rule.
To use Cramer’s rule, the equations are written as a1x + b1y = c1 and a2x + b2y = c2
Coefficient of x is a1 and a2, coefficient of y is b1 and b2, coefficient of constant terms is c1 and c2 then
D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\) - In D the column of constants \(\begin{pmatrix} c_1\\c_2 \end{pmatrix}\) is omitted
Dx = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\) - In Dx the column of the coefficients of x, \(\begin{pmatrix} a_1\\a_2 \end{pmatrix}\) is replaced by \(\begin{pmatrix} c_1\\c_2 \end{pmatrix}\)
Dy = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\)- In Dy the column of the coefficients of y, \(\begin{pmatrix} b_1\\b_2 \end{pmatrix}\) is replaced by \(\begin{pmatrix} c_1\\c_2 \end{pmatrix}\)
\(x=\frac{D_x}{D}\) and \(y=\frac{D_y}{D}\)
Cramer’s method to solve simultaneous equations :
Write given equations in the form ax + by = c .
Find the values of determinants D using D = \(\begin{vmatrix} a_1 &b_1 \\ a_2& b_2 \end{vmatrix}\)
Find the values of determinants Dx using Dx = \(\begin{vmatrix} c_1 &b_1 \\ c_2& b_2 \end{vmatrix}\)
and Find the values of determinants Dy using Dy = \(\begin{vmatrix} a_1 &c_1 \\ a_2& c_2 \end{vmatrix}\)
Using, \(x=\frac{D_x}{D}\) and \(y=\frac{D_y}{D}\) find values of x, y.
Activity : (Textbook page)
To solve the simultaneous equations by determinant method, fill in the blanks :
y + 2x – 19 = 0; 2x – 3y + 3 = 0.
Solution : Write the given equations in the form ax + by = c. 2x + y = 19 2x – 3y = –3 D = \(\begin{vmatrix} 2 & 1 \\ 2& -3 \end{vmatrix}\) = ([2]x-3)-(2x[1]) = [-6] – [2] = [–8] Dx = \(\begin{vmatrix} 19 & 1 \\ -3& -3 \end{vmatrix}\) = (19 x[-3])-([-3]x[1]) = [–57] – [–3] = [–54] Dy = \(\begin{vmatrix} 2 & 19 \\ 2& -3 \end{vmatrix}\) = ([2]x[-3])-([2]x[19]) = [–6] – [38] = [–44] By Cramer’s Rule – \(x=\frac{D_x}{D} = \frac{-54}{-8} = \frac{27}{4}\) and \(y=\frac{D_y}{D}=\frac{-44}{-8}=\frac{11}{2}\) ∴ \((x,y)=(\frac{27}{4},\frac{11}{2})\) is the solution of the given equation
Activity 2 : Complete the following activity –
3x – 2y = 3, 2x + y = 16
Find the values of determinants in the given equations
D = \(\begin{vmatrix} 3 & -2 \\ 2& 1 \end{vmatrix}\) = (3x1)–(2x–2) = [7] Dx = \(\begin{vmatrix} 3 & -2 \\ 16& 1 \end{vmatrix}\) = (3x1)–(16 x –2) = [35] Dy = \(\begin{vmatrix} 3 & 3 \\ 2&16 \end{vmatrix}\) = (3x16)–(2 x 3) = [42] Values according to Cramer’s Rule \(x=\frac{D_x}{D} = \frac{35}{7}\) = [5] \(y=\frac{D_y}{D}=\frac{42}{7}\) = [6] ∴ (x,y) = ([5], [6]) is the solution.
Let’s think (Textbook)
Q What is the nature of the solution if D = 0?
D = \(\begin{vmatrix} a_1 & b_1 \\ a_2& b_2 \end{vmatrix}\) If D = 0, then a1b2 – b1a2 = 0. Or \(\frac{a_1}{a_2}= \frac{b_1}{b_2}\) ∴ The two simultaneous equations have either no solution or infinite solutions. It means the two simultaneous equations do not have a unique solution.
Q What can you say about lines if common solution is not possible?
If the common solution about the lines is not possible, then the lines are parallel to each other or coincide.
Equations reducible to a pair of linear equations in two variables :
Activity : Complete the following table.
In the above table the equations are not linear. We can create new variables making a proper change in the given variables. Substituting the new variables in the given non-linear equations, we can convert them in linear equations. Remember that the denominator of any fraction of the form \(\frac mn\) cannot be zero.
Equation
No. of variables
whether linear or not
\(\frac{3}{x}-\frac{4}{y}\)= 8
2
Not linear
\(\frac{6}{x-1}+\frac{3}{y-2}\)= 0
2
Not linear
\(\frac{7}{2x+1}+\frac{13}{y+2}\)= 0
2
Not linear
\(\frac{14}{x+y}+\frac{3}{x-y}\)= 5
2
Not linear
Let’s Study the following example :
\(\frac{4}{x}+\frac{5}{y}\)= 7; \(\frac{3}{x}+\frac{4}{y}\)= 5
\(4(\frac{1}{x})+5(\frac{1}{y})\)= 7 .....(1) \(3(\frac{1}{x})+4(\frac{1}{y})\)= 5 ....(2) Substituting a for \(\frac{1}{x}\) and b for \(\frac{1}{y}\) , 4a + 5b = 7 …..(3) 3a + 4b = 5 …..(4) These are linear equations in variables a and b. Multiplying both the sides of equation (3) by 4 and equation (4) by 5, And subtracting equation (6) from equation (5) \(\begin{array}{rrrrrrr} Substituting a = 3 in equation (3), 4(3) + 5b = 7 ∴ 12 + 5b = 7 ∴ 5b =7 – 12; \ 5b = –5 b = –1. Now, a = \(\frac{1}{x}\) = 3 ∴ x = \(\frac{1}{3}\); b = \(\frac{1}{y}\) = –1 ∴ y = –1 Answer- (x, y) = \((\frac{1}{3},-1)\) is the solution of the given simultaneous equations.
& 16a & + & 20b & = & 28 &\text{…..(2)}\\
- & & & & & & \\
&15a & + & 20b & = & 25 &\text{…..(3)} \\
-& & -& & &-& \\ \hline
& a & & & = & 3 & \\
\end{array}\)
Activity : To solve given equations fill the boxes below suitably.
\(\frac{5}{x-1}+\frac{1}{y-2}\)= 2; \(\frac{6}{x-1}-\frac{3}{y-2}\)= 1
Replacing \(\frac{1}{x-1}\) by m \(\frac{1}{y-2}\) by n ∴ 5m + n = 2; 6m - n = 1 New equations on solving : Multiplying (5m + n = 2) by 3 ∴ 15m + 3n = 6 \(\begin{array}{rrrrrrr} ∴ m = \(\frac{7}{21}\) ∴ m = = \(\frac{1}{3}\) 15m + 3n = 6 ∴ 15 \(\frac{1}{3}\) + 3n = 6 ∴ 5 + 3n = 6, ∴ 3n = 6-5 = 1 ∴ n = \(\frac{1}{3}\) m = \(\frac{1}{3}\) ; n = \(\frac{1}{3}\) Replacing m,n by their original values \(\frac{1}{x-1}\) = \(\frac{1}{3}\) \(\frac{1}{y-2}\) = \(\frac{1}{3}\) On solving x – 1 = 3, ∴ x = 3 + 1 = 4 y – 2 = 3, ∴ y = 3 + 2 = 5 ∴ x = 4, y = 5 Answer- (x, y) = (4,5) is the solution of the given simultaneous equations.
& 15m & + & 3n & = & 6 &\text{…..(2)}\\
+ & & & & & & \\
&6m & - & 3n & = & 1 &\text{…..(3)} \\
& & & & && \\ \hline
& 21m & & & = & 7 & \\
\end{array}\)
Application of Simultaneous Equations :
Use of simultaneous equations is common in Science and Mathematics. The simultaneous equations are used to solve word problems.
To solve the problem, apply the following steps :
- Read the problem carefully. Identify the unknown quantities about which some information is supplied. Denote these quantities by variables like x, y, a, b, etc.
- Concentrate on each phrase of the problem one by one. Write the equation in terms of the variables which these phrases suggest.
- Solve the equations and find the values of the variables and write the answer.
Activity : (Textbook )
There are some instructions given below. Frame the equations from the information and write them in the blank boxes shown below by arrows .
We reply to valid query.