Optics
Maharashtra Board-Class-11-Science-Physics-Chapter-9
Solutions
Question 1. Choose the correct option
(i) As per recent understanding light consists of
(A) rays
(B) waves
(C) corpuscles
(D) photons obeying the rules of waves
(D) photons obeying the rules of waves
(ii) Consider optically denser lenses P, Q, R and S drawn below. According to Cartesian sign convention which of these have positive focal length?

(A) Only P
(B) Only P and Q
(C) Only P and R
(D) Only Q and S
(B) Only P and Q
(iii) Two plane mirrors are inclined at angle 400 between them. Number of images seen of a tiny object kept between them is
(A) Only 8
(B) Only 9
(C) 8 or 9
(D) 9 or 10
(C) 8 or 9
(iv) A concave mirror of curvature 40 cm, used for shaving purpose produces image of double size as that of the object. Object distance must be
(A) 10 cm only
(B) 20 cm only
(C) 30 cm only
(D) 10 cm or 30 cm
(D) 10 cm or 30 cm
(v) Which of the following aberrations will NOT occur for spherical mirrors?
(A) Chromatic aberration
(B) Coma
(C) Distortion
(D) Spherical aberration
(A) Chromatic aberration
(vi) There are different fish, monkeys and water on the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
(A) 6/5
(B) 5/4
(C) 4/3
(D) 7/5
(B) 5/4
Explanation :
(vii) Consider following phenomena/applications:
P) Mirage, Q) rainbow, R) Optical fibre and S) glittering of a diamond. Total internal reflection is involved in
(A) Only R and S
(B) Only R
(C) Only P, R and S
(D) all the four
(A) Only R and S
(viii) A student uses spectacles of number -2 for seeing distant objects. Commonly used lenses for her/his spectacles are
(A) bi-concave
(B) double concave
(C) concavo-convex
(D) convexo-concave
(A) bi-concave
(ix) A spherical marble of refractive index 1.5 and curvature 1.5 cm, contains a tiny air bubble at its centre. Where will it appear when seen from outside?
(A) 1 cm inside
(B) at the centre
(C) 5/3 cm inside
(D) 2 cm inside
(C) 5/3 cm inside
(x) Select the WRONG statement.
(A) Smaller angle of prism is recommended for greater angular dispersion.
(B) Right angled isosceles glass prism is commonly used for total internal reflection.
(C) Angle of deviation is practically constant for thin prisms.
(D) For emergent ray to be possible from the second refracting surface, certain minimum angle of incidence is necessary from the first surface.
(A) Smaller angle of prism is recommended for greater angular dispersion.
(xi) Angles of deviation for extreme colours are given for different prisms. Select the one having maximum dispersive power of its material.
(A) 7°, 10°
(B) 8°, 11°
(C) 12°, 16°
(D) 10°, 14°
(A) 7°, 10°
Explanation :
(xii) Which of the following is not involved in formation of a rainbow?
(A) refraction
(B) angular dispersion
(C) angular deviation
(D) total internal reflection
(C) angular deviation
(xiii) Consider following statements regarding a simple microscope:
(P) It allows us to keep the object within the least distance of distant vision.
(Q) Image appears to be biggest if the object is at the focus.
(R) It is simply a convex lens.
(A) Only (P) is correct
(B) Only (P) and (Q) are correct
(C) Only (Q) and (R) are correct
(D) Only (P) and (R) are correct
(D) Only (P) and (R) are correct
Question 2. Answer the following questions.
(i) As per recent development, what is the nature of light? Wave optics and particle nature of light are used to explain which phenomena of light, respectively?
As per recent development,
- Physical or wave optics is used to explain phenomena that are specifically attributable to the wave nature of light, e.g., interference, diffraction, polarization, double refraction and Doppler effect.
- Quantum optics is used to describe phenomena associated with the quantum or particle nature of light, such as spectral line emission, the photoelectric effect, the Compton effect, lasers, and LEDs.
(ii) Which phenomena can be satisfactorily explained using ray optics? State the assumptions on which ray optics is based.
Geometrical or ray optics can satisfactorily explain reflection, refraction, total internal reflection and dispersion.
Ray optics is based on the following assumptions:
- Rectilinear propagation : In a homogeneous and isotropic medium, light travels in a straight line.
- When two rays cross each other, they interpenetrate without disturbing each other.
(iii) What is focal power of a spherical mirror or of a lens? What may be the reason for using P = \(\frac{1}{f}\) as its expression?
The focal power of a spherical mirror gives the degree to which a mirror can converge or diverge a parallel beam of light and is defined as the negative reciprocal of its focal length P = \(-\frac{1}{f}\)
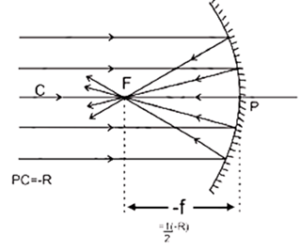
The reciprocal, \(\frac{1}{f}\) actually represents curvature of a spherical surface of which f is the radii. Figure shows plane waves reflected by a concave mirror toward its focal point F.
The lines represent the crests of light waves that are everywhere perpendicular to the corresponding light rays that could have been drawn from object at infinity to the image point at F.
The shorter the focal length f, the greater is the curvature of the reflected waves, i.e., the more is the converging power of the mirror. That is, P ∝ \(\frac{1}{f}\).
The power of a converging mirror is taken to be positive. The minus sign is included because, by sign convention, f of a concave (converging) mirror is negative.
(iv) At which positions of the objects do spherical mirrors produce
(i) diminished image, (ii) magnified image?
(i) Amongst the two types of spherical mirrors, convex mirror always produces a diminished image at all positions of the object.
Concave mirror produces diminished image when object is placed:
- Beyond radius of curvature (i.e., u > 2f)
- At infinity (i.e., u = ∞)
(ii) Concave mirror produces magnified image when the object is placed:
- between centre of curvature and focus (i.e., 2f > u > f)
- between focus and pole of the mirror (i.e., u < f)
(v) State the restrictions for having images produced by spherical mirrors to be appreciably clear.
Spherical aberration can be reduced by allowing only paraxial rays. This can be achieved by
- using a mirror of small size
- using a circular iris diaphragm, called an aperture.
With any of these two restrictions, sharp images of objects at any distance greater than the focal length may be formed on a screen, since bundles of parallel rays close to the axis and making only small angles with it are brought to a sharp focus in the focal plane.
If, however, the light is not confined to the paraxial region, parallel incident rays at
increasing distances from the principal axis cross the axis closer to the mirror, as shown in below Fig. If a small screen is placed at the paraxial focal plane F and then moved toward the mirror, a point is reached where the size of the circular image spot is a minimum. This circular spot is indicated in Fig. and is called the circle of least confusion.

(vi) Explain spherical aberration for spherical mirrors. How can it be minimized? Can it be eliminated by some curved mirrors?
(a) A spherical mirror produces a sharp image when its aperture is small compared to its focal length. But if the mirror size is large, the peripheral or abaxial rays reflected from the outer edges are brought to a focus closer to the pole than the paraxial rays. This focusing defect is called spherical aberration.
The distance between the paraxial and abaxial foci is called the longitudinal spherical aberration (LSA).
(b) Spherical aberration can be reduced by allowing only paraxial rays. This can be achieved by
- using a mirror of small size
- using a circular iris diaphragm, called an aperture.
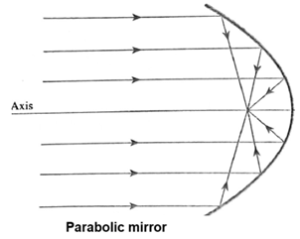
(c) As for elimination, spherical aberration can be completely removed by using mirrors with a different shape, such as a parabolic mirror.
Parabolic mirrors have a shape that causes all parallel rays (light coming from a distance) to reflect through a single focal point, thus eliminating the blurriness associated with spherical aberration. This is why parabolic mirrors are often used in telescopes and other high-precision optical instruments to produce sharp, clear images.
(vii) Define absolute refractive index and relative refractive index. Explain in brief, with an illustration for each.
(a) Absolute refractive index of a medium : Absolute refractive index, or the refractive index of a medium relative to free space, is defined as the ratio of the speed of light in free space to that in the medium.
n = \(\frac{\text{speed of light in free space}}{\text{speed of light in medium}}=\frac{c}{v}\)
(b) Relative refractive index : When a monochromatic light passes from medium 1 (in which its speed is v1) into medium 2 (in which its speed is v2), the refractive index of medium 2 relative to medium 1 is defined as the ratio of the speed of light in medium 1 to that in medium 2.
1n2 = \(\frac{\text{speed of light in in medium 1}}{\text{speed of light in medium 2}}=\frac{v_1}{v_2}\) …..(1)
The speed of light in free space (or air), c = 3 x 108 m/s. The speeds of yellow light in water and glass are 2.25 x 108 m/s and 2 x 108 m/s, respectively.
∴ The absolute refractive index, for yellow light, for water,
nw = \(\frac{c}{v_w}=\frac{3×10^8}{2.25×10^8}=\frac{3}{9/4}=\frac{3}{4}\)
and for glass ng = \(\frac{c}{v_g}=\frac{3×10^8}{2×10^8}=\frac{3}{2}\)
The refractive index of glass w.r.t. water is
wng = \(\frac{v_w}{v_g}=\frac{2.25×10^8}{2×10^8}=\frac{9/4}{2}=\frac{9}{8}\)
Also wng = \(\frac{n_g}{n_w}=\frac{3/2}{4/3}=\frac{9}{8}\)
(viii) Explain ‘mirage’ as an illustration of refraction.
Mirage: A mirage is an illusion where a pond of water appears ahead on a sunny day, but upon physical reach, the pond appears dry.
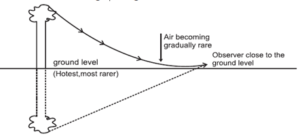
Reason :
- This occurs because the Sun heats the Earth's surface, creating a layer of hot air with a lower mass density and refractive index.
- When the vertical temperature gradient is steep, the optically rarer patch of hot air above the Earth's surface may constantly refract a beam of light back into the denser air above.
- This inverted picture, produced beneath the true location of the object, creates the illusion of the object being reflected in a pool of water.
- To see a mirage, one must be looking down a featureless surface like a desert or asphalt pavement on a calm sunny day.
(ix) Under what conditions is total internal reflection possible? Explain it with a suitable example. Define critical angle of incidence and obtain an expression for it.
Conditions for total internal reflection:
- The light ray must travel from denser medium to rarer medium.
- The angle of incidence in the denser medium must be greater than critical angle for the given pair of media.
Total internal reflection in optical fibre:
- Consider an optical fibre made up of the core of refractive index n1 and cladding of refractive index n2 such that, n1 > n2.
- When a ray of light is incident from a core (denser medium), the refracted ray is bent away from the normal.
- At a particular angle of incidence ic in the denser medium, the corresponding angle of refraction in the rarer medium is 90°.
- For angles of incidence greater than ic, the angle of refraction becomes larger than 90° and the ray does not enter into the rarer medium at all but is reflected totally into the denser medium as shown in the figure.

Critical angle : When a light ray travelling in a denser medium (of refractive index n1) meets an interface with a rarer medium (of refractive index n2), the angle of incidence in the denser medium for which the beam just emerges into the rarer medium, i.e., the angle of refraction in the rarer medium is 90°, is called the critical angle for the two mediums.
If i and r are the angles of incidence and refraction, then
n1 sin i = n2 sin r ….[Snell's law ]
At the critical angle, i = ic and r =90°, so that
n1 sin ic = n2 …[∵ sin r = sin 90 = 1]
∴ sin ic = n2/n1 = 1n2 = \(\frac{1}{_2n_1}\)
Here 2n1 is the refractive index of the denser medium relative to the rarer medium.
Hence sin ic = \(\frac{1}{_2n_1}\)
(x) Describe construction and working of an optical fibre. What are the advantages of optical fibre communication over electronic communication?

Construction :
- An optical fibre is a flexible 'light pipe' in which light is limited to move due to repeated total internal reflections.
- An optical fibre is made up of a transparent core filament and a plastic matrix known as cladding (Fig.).
- The core has a diameter of a few thousandths of a millimeter and is often composed of glass.
- The cladding's refractive index is lower than that of glass.
- Each composite filament, known as an optical fibre, is extremely flexible, and an optical transmission line is made up of a bundle of these optical fibres wrapped in a protective plastic jacket.
Working : Because the refractive index of the core is more than that of the cladding, light travels along the core by total internal reflections if it strikes the interface between the core and the cladding at an angle of incidence more than the critical angle.
Advantages of optical fibre communication :
- Large bandwidth: Uses optical carrier waves in high frequency (>100 GHz) microwave to ultraviolet regions, allowing for the transmission of several thousand different signals.
- Immunity from electromagnetic and radio frequency interferences.
- Low transmission loss: <0.2 dB/km, reducing the need for repeaters and increasing system reliability.
- High signal security: No significant radiations from optical fibres, making it ideal for military, banking, and computer network applications.
- Reliability to theft: Made of glass, not expensive metals, making it unlikely to be stolen.
- Space-saving: Small size, small bending radius, and light weight make it suitable for aircrafts.
(xi) Why is a prism binoculars preferred over traditional binoculars? Describe its working in brief.
(a) A prism binocular offers several advantages over traditional binoculars.
- It minimizes light loss, enhances objective separation, and doubles-backs light rays.
- It allowing long focus objective lenses to be used in short tubes, resulting in higher magnifying power.
- This allows for better depth perception and stereoscopic effect.
(b) Working of prism binocular :

- A prism binocular is a pair of monocular terrestrial telescopes mounted side by side, one for each of the two eyes.
- The objective lenses in front and the eyepieces at the rear are converging lenses and each tube has a pair of totally reflecting erecting prisms, Fig.
- Rays of light entering through the objectives undergo two total reflections in each prism. Each prism turns a ray by 180°, the second prism of a pair effectively turning it towards the eyepiece.
- The two prisms are mounted, with their cross sections perpendicular to each other such that the 180° turn by each produces left-right and top-down lateral inversions, thereby giving an erect final image.
(xii) A spherical surface separates two transparent media. Derive an expression that relates object and image distances with the radius of curvature for a point object. Clearly state the assumptions, if any.
- Consider a convex spherical surface APB separating two transparent mediums 1 and 2. Their absolute refractive indices are n1 and n2, respectively, with n2 > n1.
- Let O be a luminous point object on the principal axis in the rarer medium, as shown in Fig.

- The ray OP along the principal axis is incident normally on the spherical surface and passes into the denser medium undeviated.
- A second ray OD is incident obliquely on the surface at an angle of incidence i with the normal CN.
- Let the angle of refraction r for this ray be such that the refracted ray meets the ray OP forming a real point image I on the principal axis.
- The angles made by the incident ray OD, the refracted ray DI and the normal CN with the principal axis are ∝, β and γ, respectively.
Assumption : To make small angle approximations (sin θ ≈ θ and tan θ ≈ θ, θ in
radian), we consider the ray OD to be a paraxial ray (i.e., close to and almost parallel to the axis). Then, i, r, ∝, β and γ may be treated as very small angles.
Derivation : By Snell's law,
n1 sin i = n2 sin r or n1 i = n2 r
In triangles DOC and DIC, i and ν are the respective exterior angles.
∴ i = α + ν
And ν = β + r or r = ν − β
∴ n1(α + ν)= n2(ν − β)
∴ n1α + n2β = (n2 − n1)ν
Now α = \(\frac{arc\,PD}{PO}\), β = \(\frac{arc\,PD}{PI}\), ν = \(\frac{arc\,PD}{PC}\)
∴ n1\(\frac{arc\,PD}{PO}\) + n2\(\frac{arc\,PD}{PI}\) = (n2 — n1)\(\frac{arc\,PD}{PC}\)
∴ \(\frac{n_1}{PO}+\frac{n_2}{PI}=\frac{n_2-n_1}{PC}\)
According to the Cartesian Sign convention,
object distance PO= −u, image distance PI = +v and radius of curvature PC = +R
∴ \(\frac{n_1}{-u}+\frac{n_2}{v}=\frac{n_2-n_1}{R}\)
∴ \(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\)
- Note : Although this relation has been derived by considering a particular case, the application of the sign conventions makes this a general relation for refraction at a spherical surface. It is true for both convex and concave surfaces, n1 > n2 or n2 > n1, real or virtual images, and real or virtual object’s.
(xiii) Derive lens makers’ equation. Why is it called so? Under which conditions focal length f and radii of curvature R are numerically equal for a lens?
(a) Consider a thin convex lens (refractive index n2) placed in a rarer medium (refractive index n1,). Let R1 and R2 be the radii of curvature of the two spherical surfaces of the lens.
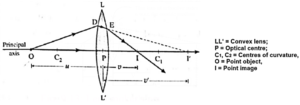
Consider a luminous point object O on the principal axis in front of the lens at a distance u from the optical centre P (Fig.).
The ray OP incident on the lens along its principal axis passes through uncleviated.
A paraxial ray OD suffers two refractions, at the two spherical surfaces of the lens.
For refraction at a spherical surface,
\(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\) ……(1)
Now, for the refraction at the first surface, the refracted ray is DE.
If there was no second surface, the ray DE would have proceeded in the denser medium and met the ray OP, thus forming a real image at I’.
Let PI’ = v’.
Thus, in this case, the object distance is u, the image distance is v’ and the radius of curvature is R1.
Substituting these values in Eq. (1),
\(\frac{n_2}{v'}-\frac{n_1}{u}=\frac{n_2-n_1}{R_1}\) ……(2)
But the denser medium does not extend far beyond the first surface so that the ray DE suffers another refraction at the second surface and emerges out into the rarer medium.
This emergent ray meets the ray OP at I which is the image produced by the lens. Let PI = v.
Thus, for the refraction at the second surface, the incident ray DE is in a medium of refractive index n2, the refracted ray is in a medium of refractive index n1, and I’ acts as the virtual object with object distance PI’ = v’.
Accordingly, Eq. (1) for this case becomes
\(\frac{n_1}{v}-\frac{n_2}{v'}=\frac{n_1-n_2}{R_2}=-\frac{n_2-n_1}{R_2}\)……(3)
Adding Eqs. (2) and (3) eliminates v’ and we get,
\(\frac{n_1}{v}-\frac{n_1}{u}\) = \((\frac{n_2}{n_1})(\frac{1}{R_1}-\frac{1}{R_2})\)
or, dividing by n1,
\(\frac{1}{v}-\frac{1}{u}\) = (n2-n1)\((\frac{1}{R_1}-\frac{1}{R_2})\) ……(4)
The focal length of a lens is the image distance when the object is at infinity, i.e., v = f for u = ∞. Substituting these values in Eq. (4),
\(\frac{1}{f}\) = (1n2 − 1)\((\frac{1}{R_1}-\frac{1}{R_2})\) ……(5)
Where 1n2 = \(\frac{n_2}{n_1}\)
Equation (5) is called the lens makers’ equation.
(b) Makers of lenses for spectacles and optical instruments use the equation to decide the radii of curvature of a lens for the chosen type of glass or acrylic, i.e., after choosing a medium of certain refractive index. Hence is called the lens makers’ equation.
(c) Conditions for focal length f and radii of curvature R are numerically equal for a lens :
The focal length and radii of curvature are numerically equal for a thin, symmetric lens — either double convex or double concave — made of the common crown glass, whose refractive index, n ≈ 1.5.
For an equiconvex lens, by the sign convention, R1= R and R2 = −R (R>0). Then, by lens makers’ formula,
\(\frac{1}{f}\) = (n − 1)\((\frac{1}{R_1}-\frac{1}{R_2})\)
= (n − 1)\((\frac{1}{R}-\frac{1}{-R})\)
= \(\frac{2(n-1)}{R}\)
∴ For n = 1.5, \(\frac{1}{f}\) = (n − 1)\(\frac{2(1.5-1)}{R}=\frac{1}{R}\)
∴ f = R
For an equiconcave lens, R1 = − R and R2 = R
∴ \(\frac{1}{f}\) = (n — 1)\((\frac{1}{-R}-\frac{1}{R})\) = \(-\frac{2(n-1)}{R}\)
∴ For n = 1.5 , \(\frac{1}{f}=-\frac{1}{R}\)
∴ f = −R
Question 3. Answer the following questions in detail.
(i) What are different types of dispersions of light? Why do they occur?
Types of dispersions of light :
(a) Angular dispersion : The angular separation between the two extreme rays of different colours in the dispersed beam of a polychromatic light is called the angular dispersion.
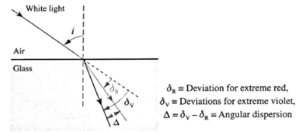
(b) Lateral dispersion : When a monochromatic ray of light, obliquely incident on one surface of a parallel-plate glass slab, the ray emerges through the opposite surface parallel to the incident direction but laterally displaced.
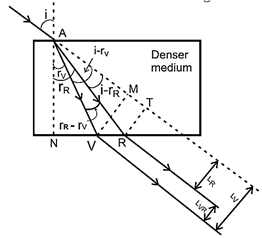
Reasons for occurrence :
- When a narrow collimated beam of white light in free space or air is obliquely incident on such a glass slab, it passes into the glass with its constituent colours angularly dispersed, (see above Fig.)
- But as the refracted rays emerge into air through the parallel surface, they undergo deviations equal and opposite to those at the first surface.
- Hence, the emergent rays of all the colours are parallel to each other and to the incident direction, but laterally displaced with different lateral displacements.
(ii) Define angular dispersion for a prism. Obtain its expression for a thin prism. Relate it with the refractive indices of the material of the prism for corresponding colours.
Angular dispersion for a prism : If a polychromatic beam is an incident upon a prism, the emergent beam consists of all the individual colours angularly separated. This phenomenon is known as angular dispersion for a prism.
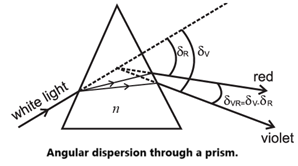
Expression : Suppose, for two colours 1 and 2, the material of a thin prism has refractive indices n1 and n2 with n2 > n1. Let the deviations for the two colours be δ1 and δ2, respectively. For a thin prism,
δ = A(n - 1)
δ2 > δ1 for n2 > n1
∴ Angular dispersion for the two colours,
δ21 = δ2 — δ1 = A(n2—1) — A(n1—1)
= A(n2 — n1)
For White light :
δVR = δV — δR
= A(nV — 1) — A(nR — 1) = = A(nV — nR)
(iii) Explain and define dispersive power of a transparent material. Obtain its expressions in terms of angles of deviation and refractive indices.
Dispersive power:
- Ability of an optical material to disperse constituent colours is its dispersive power.
- It is measured for any two colours as the ratio of angular dispersion to the mean deviation for those two colours.
Expressions for dispersive power of a transparent material in terms of angles of deviation and refractive indices :
When white light is dispersed, the deviation is maximum for the extreme violet ray (δV) and minimum for the extreme red ray (δR). The deviation for yellow ray δY is approximately intermediate between them. Then, the angular dispersion between the rays of the extreme colours is Δ = δV — δR
∴ The dispersive power of the material of the prism is
ω = (angular dispersion)/(angle of deviation of mean colour)
= \(\frac{Δ}{δ_Y}=\frac{δ_V-δ_R}{δ_Y}\) …..(1)
Let nV, nR and nY be the refractive indices of the material of the prism for violet, red and yellow light, and δV, δR and δY be the corresponding angles of minimum deviation, respectively.
For a thin prism, δ = A(n — 1)
∴ δV = A(nV — 1), δR = A(nR — 1) and δY = A(nY — 1)
Then, from Eq. (1),
ω = \(\frac{Δ}{δ_Y}=\frac{δ_V-δ_R}{δ_Y}\)
∴ ω = \(\frac{A(n_V-n_g)}{A(n_Y-1)}=\frac{n_V-n_g}{n_Y-1}\) …..(2)
Equations (1) and (2) give the required expressions.
(iv) (a) State the conditions under which a rainbow can be seen.
(b) Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
(c) Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
(d) Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
(a) Conditions for observing a rainbow from the ground :
- Dark rain-bearing clouds with relatively large raindrops.
- The sun must not be more than 42° above the horizon. Thus, it is possible to see a rainbow in the morning a few hours before noon and in the afternoon a few hours afternoon.
- The sun must be behind the observer and not obscured by clouds.
(b) A rainbow is caused by the dispersion of the sunlight into its constituent colours by the water droplets present in the clouds. The brighter rainbow usually seen is the primary rainbow. At each water drop, the sunlight refracts into it, gets internally reflected once and emerges out with a second refraction.
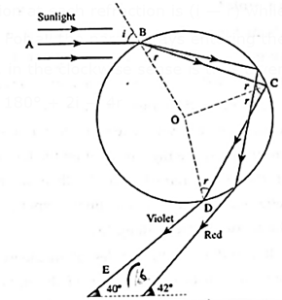
As shown in Fig. the deviation at each refraction is (i - r) while at each internal reflection it is (180° - 2r). For all the parallel rays entering the upper half of the drop, the total deviation, δ, in the clockwise sense is thus given by
δ = 2 (i- r) + (180° - 2r) = 180° + 2i - 4r
- The value for this deviation is 137°42' for red light and 139°37' for violet light. Thus, an observer standing with his back to the Sun receives these rays for the red light at an angle of 180° - 137°42' = 42°18' with the line joining the Sun to him, and those for the violet light at 180° - 139°37' = 40°23' with this line.
- Therefore, this primary bow is violet in colour on the lower side and red on the upper, the other colours falling in between. The rainbow appears curved like a bow because this phenomenon is the same in all planes passing through the line.
- For a primary bow to be visible to an observer on the ground, the Sun must not be more than 42° above the horizon.
(c) Formation of a secondary rainbow :
Sometimes, when a primary rainbow is seen, a fainter secondary bow is seen higher in the sky. It is formed by the sunrays undergoing two refractions and two internal reflections at each water drop, Fig.
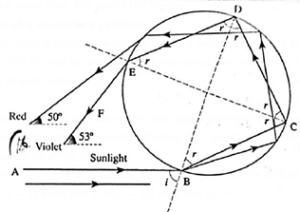
The secondary rainbow is produced by the rays incident on the lower half of the drop, refracted at B, then internally reflected at C and D, and finally emerges into
the air downwards along EF.
If i and r are the angles of incidence and refraction at B, the deviation of the light at B and E is (i — r) each and (180° — 2r) at C and D.
Sometimes, when a primary rainbow is seen, a fainter secondary bow is seen higher in the sky. It is formed by the sunrays undergoing two refractions and two internal reflections at each water drop, Fig.
The secondary rainbow is produced by the rays incident on the lower half of the drop, refracted at B, then internally reflected at C and D, and finally emerges into the air downwards along EF.
If i and r are the angles of incidence and refraction at B, the deviation of the light at B and E is (i — r) each and (180° — 2r) at C and D.
For all the parallel rays entering the lower half of the drop, the total deviation, δ, in the anticlockwise sense is thus given by
δ = 2(i — r) + 2(180°—2r)
= 360° + 2i — 6r
The deviation is such that the observer, looking away from the Sun, sees the red colour in an arc subtending an angle of 50°34’ and the violet at an angle of 54° with the line joining the Sun to the observer.
Therefore, the secondary or the outer bow is violet on the outside and red on the inside, in reverse order of the colours as compared with the primary bow.
(d) Yes it is possible,
Conditions :
- A primary rainbow can sometimes be seen alongside a fainter secondary rainbow.
- The primary rainbow is formed by sunlight entering the tops of properly located drops and undergoing internal reflection before refracting out.
- The secondary rainbow, on the other hand, arises from sunlight entering the lower halves of the drops and undergoes two internal reflections before refracting out.
- To see both rainbows simultaneously, dark rain-bearing clouds in the 40°-55° range must be visible and sufficiently intense sunlight must be incident on them from behind the observer.
(v) (a) Explain chromatic aberration for spherical lenses. State a method to minimize or eliminate it.
(b) What is achromatism? Derive a condition to achieve achromatism for a lens combination. State the conditions for it to be converging.
(a) Chromatic aberration : Chromatic aberration is a lens defect caused by the refractive index of the lens, resulting in violet light being deviated more than red light, and other colours being centered at different points. This defect causes constituent colors of a collimated white light beam to be focused at different points.
If the collimated beam is parallel to the principal axis, the axial distance between two focal points for extreme colours is called the axial or longitudinal chromatic
aberration (ACA).
ACA = fR — fV
Since violet light deviates the most, fV is closer to the lens than fR. For a positive lens (convex), ACA is positive; for a negative lens (concave), ACA is negative.
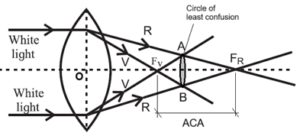
For a distant point object, a convex lens casts a real image surrounded by a circular halo. If the screen is moved nearer the lens, the image is blurred with a orange-red halo. Moving the screen away from the lens — beyond the best image — the image is again blurred but with a blue-violet halo. The position of the best image is the location of the circle of least confusion.
The image of an off-axis point for different colours will be formed at different distances from the principal axis. The vertical distance between two such points for extreme colours is called the lateral chromatic aberration (LCA).
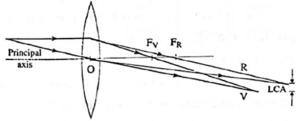
Eliminating chromatic aberration :
Elimination of chromatic aberration for all colours is impossible. However, a combination of two thin lenses in contact, one convex and one concave and of two materials forming the lenses, can be used to eliminate the total dispersion for two specific colours. Such an arrangement is said to be achromatized for those two specific colours and is called an achromat.
(b) Achromatism is the condition for a combination of two thin lenses so as to eliminate the chromatic aberration for two specific colours.
Condition for achromatism :
An achromatic combination aims to eliminate the total dispersion for two specific colours by using materials of different dispersive powers, ω1 and ω2 forming the lenses.
By the lens—makers’ formula,
\(\frac{1}{f}\) = (n—1)\(9\frac{1}{R_1}-\frac{1}{R_2})\) = (n—1)K
Abbreviating the notation for brevity, for the two lenses,
\(\frac{1}{f_1}\) = (n1 — 1)K1 and \(\frac{1}{f_2}\) = (n2 — 1)K2
For each lens of the combination, n and f vary with colour while K is constant. For two lenses in contact,
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\) = (n1 — 1)K1 + (n2 — 1)K2
= (n1K1 + n2K2) — (K1 + K2)
This expression will give the focal length of the achromatic doublet for red (fR) and violet (fV) when the appropriate refractive indices are used. For fR = fV,
\(\frac{1}{f_{1R}}+\frac{1}{f_{2R}}=\frac{1}{f_{1V}}+\frac{1}{f_{2V}}\)
∴ (n1RK1 + n2RK2) — (K1 + K2) = (n1VK1 + n2VK2) — (K1 + K2)
∴ (n1RK1 + n2RK2) = (n1VK1 + n2VK2)
∴ n1RK1 — n1VK1 = n2VK2 — n2RK2
∴ (n1R — n1V)K1 = (n2V — n2R)K2
∴ — (n1V — n1R)K1 = (n2V — n2R)K2
\(\frac{K_1}{K_2}=-\frac{n_{2V}-n_{2R}}{n_{1V}-n_{1R}}\) ……(1)
The focal length of the doublet can conveniently be specified as fY the focal length
for yellow light, which is roughly midway between the red and violet extremes.
\(\frac{1}{f_{1Y}}\) = (n1Y — 1)K1 and \(\frac{1}{f_{2Y}}\) = (n2Y — 1)K2
∴ \(\frac{f_{2Y}}{f_{1Y}}=\frac{n_{1Y}-1}{n_{2Y}-1}.\frac{K_1}{K_2}\) ……(2)
∴ \(\frac{f_{2Y}}{f_{1Y}}=\frac{n_{2V}-n_{2R}}{n_{2Y}-1}.\frac{n_{1Y}-1}{n_{1V}-n_{1R}}\) …..[from eq(1)]
= \(-\frac{ω_2}{ω_1}\) ……(3)
Equation (3) is the condition for achromatism.
Since dispersive powers are always positive, one lens of the achromatic doublet must be a positive or converging lens and the other a negative or diverging lens.
If the second lens is a concave lens, f2Y is negative.
∴ \(\frac{1}{f_Y}=\frac{1}{f_{1Y}}+\frac{1}{f_{2Y}}\)
For the combination to be converging, i.e., for fY > 0, f1Y < f2Y so that, from Eq.(3),
ω2 > ω1
Thus, in an achromat, the first lens is a convex lens of lower dispersive power than the second lens which is a concave lens.
(vi) Describe spherical aberration for spherical lenses. What are different ways to minimize or eliminate it?
Spherical aberration :
Longitudinal spherical aberration, transverse spherical aberration and circle of least confusion are defined in the same manner as that for spherical mirrors.
- Spherical aberration of a spherical lens is a focusing defect due to its spherical surfaces.
- A spherical lens forms reasonably sharp image if its aperture is small compared with its focal length and object and image distances. But if the aperture is large, the peripheral or abaxial rays refracted from the outer edges are brought to a focus closer to the optical centre than the paraxial rays, with varying focal lengths for rays in between. This focusing defect is called spherical aberration.
- It causes the image to look hazy due to lack of sharpness.
Figure shows rays incident parallel to the optical axis from a very distant on-axis point object.
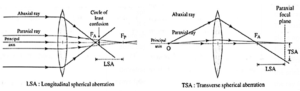
- On refraction, the paraxial rays meet at the paraxial focal point F2, while the abaxial rays fall short by a large amount.
- Rotating this diagram about the principal axis reveals a very blurry circular image in the paraxial plane.
- The least blurry image is produced a short distance to the left of the paraxial focal plane and is called the circle of least confusion.
- Figure shows how the spherical aberrations are quantitatively defined.
- The distance between the paraxial focal plane and the point where the ray crosses the principal axis is called the longitudinal spherical aberration (LSA). The distance of the ray from the principal axis at the pamxial focal plane is called the transverse spherical aberration (TSA).
Methods to reduce/eliminate spherical aberration of lenses:
- Cheapest method to reduce the spherical aberration is to use a planoconvex or planoconcave lens with curved side facing the incident rays (real object). Reversing it increases the aberration appreciably.
- Certain ratio of radii of curvature for a given refractive index almost eliminates the spherical aberration. For n = 5, the ratio is
\(\frac{R_1}{R_2}=\frac{1}{6}\) and for n = 2, it is \(\frac{1}{5}\)
- Use of two thin converging lenses separated by distance equal to difference between their focal lengths with lens of larger focal length facing the incident rays considerably reduces spherical aberration.
- Spherical aberration of a convex lens is positive (for real image), while that of a concave lens is negative. Thus, a suitable combination of them (preferably a double convex lens of smaller focal length and a planoconcave lens of greater focal length) can completely eliminate spherical aberration.
(vii) Define and describe magnifying power of an optical instrument. How does it differ from linear or lateral magnification?
Magnifying power: The magnifying power of a microscope (simple and compound) is defined as the ratio of the visual angle subtended by the image at the eye to that subtended by the object held at the least distance of distinct vision and viewed directly.
The magnifying power (M) of a simple microscope is given by
M = β/α
The lateral magnification produced by a lens is the factor by which the image size is changed from the object size.
Lateral magnification, m = hi/ho = v/u
where ho = object height, hi = image height, u = object distance, and v =image distance.
If the object is positioned at the focal point of the lens (u = f), the virtual image is at ∞ (v = ∞).
Thus, m approaches infinity as u → f.
In marked contrast, the angular magnification or magnifying power of a single lens merely decreases by 1 under the same circumstances.
(viii) Derive an expression for magnifying power of a simple microscope. Obtain its minimum and maximum values in terms of its focal length.
If a small object is seen directly without any strain on the eye, it subtends the maximum visual angle at the eye when it is at the least distance of distinct vision. Let this angle of α, as shown in Fig. (a).
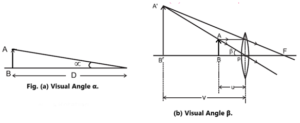
A simple microscope is a convex lens of short focal length placed between the object and the eye such that the object lies just within the focal length of the lens and the magnified virtual image is formed at the least distance of distinct vision.
The image subtends an angle β at the lens, Fig. (b). However, as the image is observed by keeping the eye close to the lens, β is also the angle subtended by the image at the eye.
The magnifying power (M) of a simple microscope is given by
M = β/α
Since the object being viewed is very small. the angles α and β are also small. With the angles measured in radian, we can use the small angle approximation. Therefore,
α ≈ tan α = BA/D ……[from fig (a)]
β = tan β = B’A’/v = BA/PB = BA/u ……[from fig (b)]
∴ M = \(\frac{β}{α}=(\frac{BA}{u})(\frac{D}{BA})=\frac{D}{u}\)
Maximum and minimum value in terms of focal length :
The focal length of a convex lens is given by
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
In this case, f is positive and u and v are both negative as per the Cartesian sign convention.
∴ \(\frac{1}{f}=-\frac{1}{v}-(-\frac{1}{u})\)
∴ \(\frac{1}{u}=\frac{1}{v}+\frac{1}{f}\)
∴ magnifying power, M = \(\frac{D}{u}=\frac{D}{v}+\frac{D}{f}\) ….(1)
Case (i) : For maximum magnifying power (Image is near point of the eye), the image should be nearest possible, i.e., at D.
When the image is formed at the least distance of distinct vision, v = D.
∴ M = \(\frac{D}{v}+\frac{D}{f}=\frac{D}{D}+\frac{D}{f}\) = \(1+\frac{D}{f}\) ….(2)
This is the maximum value of the magnifying power
Case (ii) : For minimum magnifying power (Image is far point of the eye), v = ∞ i.e., u = f (numerically)
∴ M = \(\frac{D}{v}+\frac{D}{f}=\frac{D}{∞}+\frac{D}{f}\) = \(\frac{D}{f}\) …..(3)
This is the minimum value of the magnifying power.
(ix) Derive the expressions for the magnifying power and the length of a compound microscope using two convex lenses.
Expressions for the magnifying power and length of a compound microscope using two convex lenses :
Derivation: Let at be the visual angle subtended by a small object AB when it is held at the near point of the eye and viewed directly.
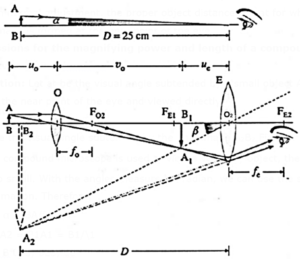
Let β be the visual angle subtended by the final image A2B2 Fig.
Since a compound microscope is used to view a very tiny object, the angles α and β are also small. With the angles measured in radian, we can use the small angle approximation.
Therefore,
α ≈ tan α = \(\frac{BA}{D}\) and
β ≈ tan β = \(\frac{B_2A_2}{O_2B_2}=\frac{B_1A_1}{O_2B_1}=\frac{B_1A_1}{u_e}\)
where D = least distance of distinct vision, and ue = distance of the intermediate image A1B1 from the eyepiece.
Let uo and vo be the object and image distances for the objective. The magnifying power M of the compound microscope is given by,
M = \(\frac{β}{α}= \frac{B_1A_1/u_e}{AB/D}=\frac{A_1B_1}{AB}×\frac{D}{u_e}\)
In this case, \(\frac{A_1B_1}{AB}=\frac{v_0}{u_0}\) = m0 = lateral magnification produced by the objective and
\(\frac{D}{u_e}\) = Me = magnifying power of the eyepiece.
∴ M = m0 x Me
Thus, the magnifying power of a compound microscope is equal to the product of
(i) the lateral magnification produced by the objective and
(ii) the magnifying power of the eyepiece, acting as a simple microscope.
Case (I) : Final image at the near point of the eye (Normal adjustment) :
Me = 1 + \(\frac{D}{f_e}\)
∴ M = m0 x Me = \(\frac{v_0}{u_0}(1+\frac{D}{f_e})\)
This is the maximum value of the magnifying power.
Case (II) : Final image at the far point of the eye :
Me = \(\frac{D}{f_e}\), ∴ M = m0 x Me = \(\frac{v_0}{u_0}×\frac{D}{f_e}\)
This is the minimum value of the magnifying power.
The length of a compound microscope = the distance between the objective and eyepiece = v0 + ue
(x) What is a terrestrial telescope and an astronomical telescope?
Terrestrial telescopes :
- A terrestrial telescope is one which is used for viewing distant objects on the Earth.
- For terrestrial telescopes the objects to be seen are on the Earth, like mountains, trees, players playing a match in a stadium, etc.
- In such case, the final image must be erect. Eye lens used for this purpose must be concave and such a telescope is popularly called a binocular.
- A variety of binoculars use three convex lenses with proper separation. The third lens again inverts the second intermediate image and makes final image erect with respect to the object.
Astronomical telescope :
- An astronomical retracting telescope consists of two converging lenses or lens systems mounted coaxially at the two ends of a metal tube.
- One of the lens systems, called the objective, has a large focal length, fo, and large aperture and is aimed at faint astronomical objects.
- The second converging lens system, called the eyepiece or ocular, has a much smaller focal length, fe, and smaller aperture.
(xi) Obtain the expressions for magnifying power and the length of an astronomical telescope under normal adjustments.
Since the object distance is practically infinite, the visual angle subtended by the object at the unaided eye, α is the same as that subtended by the parallel rays at the objective. A celestial object at an astronomical distance appears very small and so α is very small.
Also, the parallel rays from the object are brought to a focus at the focal plane of the
objective. Therefore, O1B1 = fo and, in the small angle approximation,
α ≈ tan α = \(\frac{B_1A_1}{O_1B_1}=\frac{B_1A_1}{f_o}\)
In the normal adjustment, O2B1 = fe the focal length of the eyepiece. The angle β subtended by the final image at the far point of the eye is very small and the same as that subtended by the intermediate image AIB1.
β ≈ tan β = \(\frac{B_1A_1}{O_2B_1}=\frac{B_1A_1}{f_e}\)
Therefore, the magnifying power of a telescope in normal adjustment is
M = \(\frac{β}{α}=\frac{B_1A_1}{f_e}×\frac{f_o}{B_1A_1}=\frac{f_o}{f_e}\)
Thus, the magnifying power of a telescope is equal to the ratio of the focal length of the objective to that of the eyepiece. Therefore, for greater magnifying power, the focal length of the objective must be large and that of the eyepiece small.
The length of an astronomical refracting telescope for normal adjustment = fo + fe.
(xii) What are the limitations in increasing the magnifying powers of (i) simple microscope (ii) compound microscope (iii) astronomical telescope?
(1) The magnifying power (MP) of a simple microscope is inversely proportional to its focal length. Therefore, greater MP requires and radii to be small, resulting in a thick lens, small field of view and large spherical and chromatic aberrations. The simplest single-lens magnifiers are limited by aberrations to MP of 2 to 3.
Highly corrected, high-power magnifiers (10 to 20) have achromatic doublet or triplet lenses, but are small and expensive.
(2) MP of a compound microscope is the product of the lateral magnification (m.) of the objective and the magnifying power (Me) of the eyepiece.
M = m0 x Me = \(\frac{v_0}{u_0}(1+\frac{D}{f_e})\)
Therefore, greater M requires increase in mo and / or Me.
mo may be increased by decreasing u0, but then v0 also increases correspondingly. Since the tube length of a compound microscope, L = v0 + ue, increase in mo is limited by L. Both magnification (e.g. 10 x , 20 x , etc.) and the tube length for which the objective was designed (usually 160 mm or ∞) are inscribed on the
objective barrel.
(3) MP of a telescope is equal to the ratio of the focal length of the objective to that of the eyepiece.
M = \(\frac{f_0}{f_e}\)
Therefore, for greater MP, f0 must be large and fe must be small. f0 and fe fix the length of the telescope : L = f0 + fe.
Question 4. Solve the following numerical examples
(i) A monochromatic ray of light strike the water (n = 4/3) surface in a cylindrical vessel at angle of incidence 530. Depth of water is 36 cm. After striking the water surface, how long will the light take to reach the bottom of the vessel? [Angles of the most popular Pythagorean triangle of sides in the ratio 3:4:5 are nearly 370, 530 and 900]
Given : anw = \(\frac{4}{3}\), i = 530 , D = 36 cm, c = 3 × 108 m/s
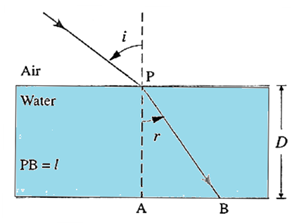
anw = \(\frac{sin\,i}{sin\,r}\)
∴ sin r = \(\frac{sin\,i}{_an_w}=\frac{sin\,53^0}{4/3}\)
∴ sin r = \(\frac{3}{4}\) × 0.7686 = 0.5765
∴ r = sin-1 0.5765 = 35012’
From fig. l cos r = D
If v is the speed of light in water,
l = vt = \(\frac{D}{cos\,r}\) …..(1)
Also anw = \(\frac{c}{v}\), ∴ v = \(\frac{c}{_an_w}\) …..(2)
∴ From eqs. (1) and (2)
t = \(\frac{_an_wD}{c\,cos\,r}\) = \(\frac{4}{3}×\frac{0.36}{(3×10^8)cos\,35^012'}\)
= \(\frac{0.16×10^{-8}}{0.8171}\) ≈ 0.2 × 10−8 = 2 × 10−9 = 2 ns
(ii) Estimate the number of images produced if a tiny object is kept in between two plane mirrors inclined at 350, 360, 400 and 450.
Given: θ1 = 35°, θ2 = 36°, θ3 = 40°, θ4 = 45°
(1) n1 = \(\frac{360^0}{θ_1}=\frac{360^0}{35^0}\) = 10.28
Since n1 is not an integer, m1 = floor (n1)
= floor (10.28) = 10,
The number of images, N1 = 10.
(1) n2 = \(\frac{360^0}{θ_2}=\frac{360^0}{36^0}\) = 10
Since n2 is an even integer, N2 = n2 — 1 = 9.
(3) n3 = \(\frac{360^0}{θ_3}=\frac{360^0}{40^0}\) = 9
Since n3 is an odd integer,
N3 = n3 = 9 (for an object on the angle bisector)
or N3 = n3 -1 = 8 (for an object off the angle bisector)
(4) n4 = \(\frac{360^0}{θ_1}=\frac{360^0}{45^0}\) = 8
Since n4 is an even integer, N4 = n4 — 1 = 7.
Answer : 10, 9, 9 or 8, 7 images respectively
(iii) A rectangular sheet of length 30 cm and breadth 3 cm is kept on the principal axis of a concave mirror of focal length 30 cm. Draw the image formed by the mirror on the same ray diagram, as far as possible on scale.
Note : Since the exact position and orientation of the object are not given, the question is vague and has no unique answer.
(iv) A car uses a convex mirror of curvature 1.2 m as its rear-view mirror. A minibus of cross section 2.4 m × 2.4 m is 6.6 m away from the mirror. Estimate the image size.
Given : R = 1.2 m, u = - 6.6 m, ho = 2.2 m
f = \(\frac{R}{2}\) = 0.6 m
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
∴ \(\frac{u}{f}=\frac{u}{v}+1\)
∴ \(\frac{u}{v}=\frac{u}{f}-1=\frac{u-f}{f}\)
∴ \(\frac{v}{u}=\frac{f}{u-f}\)
Lateral magnification, m = \(\frac{h_1}{h_0}=-\frac{v}{u}\)
∴ \(\frac{h_1}{h_0}=-\frac{f}{u-f}=\frac{f}{f-u}\)
∴ h1 = \(h_0\frac{f}{f-u}=2.2\frac{0.6}{0.6-(-6.6)}=\frac{2.2×0.6}{7.2}=\frac{2.2}{12}\) = 0.2 m
Answer : A square of edge 0.2 m
(v) A glass slab of thickness 2.5 cm having refractive index 5/3 is kept on an ink spot. A transparent beaker of very thin bottom, containing water of refractive index 4/3 up to 8 cm, is kept on the glass block. Calculate apparent depth of the ink spot when seen from the outside air.
Given : ang = \(\frac{5}{3}\), thickness of glass (D1) = 2.5 cm, anw = \(\frac{4}{3}\), Depth of water = 8 cm

When observed from water,
wng = \(\frac{D_1}{d_1}\) and the apparent depth of the ink spot is
d1 = \(\frac{D_1}{_wn_g}=\frac{D_1}{_an_g/_an_w}\)
= \(\frac{_an_w}{_an_g}D_1\) = \(\frac{4/3}{5/3}(2.5)\) = 2 cm
∴ When observed from air,
the real depth, D2 = depth of water + d1 = 8 cm + 2 cm = 10 cm
∴ The apparent depth, d2 = \(\frac{D_2}{_an_w}=\frac{10}{4/3}\) = 7.5 cm
(vi) A convex lens held some distance above a 6 cm long pencil produces its image of SOME size. On shifting the lens by a distance equal to its focal length, it again produces the image of the SAME size as earlier. Determine the image size.
The given conditions are possible only if a virtual image is formed in the first case and an inverted image of the same size is formed in the second case, as illustrated in Fig. below.

In the first case, Fig. (a), u = −u1 and v = −v1. The magnification,
m1 = \(\frac{v}{u}=\frac{-v_1}{-u_1}=\frac{v_1}{u_1}\)
and \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{-v_1}-\frac{1}{-u_1}=-\frac{1}{v_1}+\frac{1}{u_1}\) ….(1)
In the second case, Fig. (b), u = u2 = — (u1 + f) and v = v2. The magnification,
m2 = \(\frac{v}{u}=\frac{v_2}{-u_2}\)
and \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{v_2}+\frac{1}{u_2}\) ….(2)
Given : | m1 | = | m2|
∴ m1 = - m2
∴ \(\frac{v_1}{u_1}=-(-\frac{v_2}{u_2})=\frac{v_2}{u_2}\)
∴ \(\frac{v_1}{v_2}=\frac{u_1}{u_2}=\frac{u_1}{u_1+f}\) ….(3)
From Eqs. (1) and (2), equating the right hand sides,
\(\frac{1}{u_1}-\frac{1}{v_1}=\frac{1}{v_2}+\frac{1}{u_2}\)
∴ \(\frac{1}{v_1}+\frac{1}{v_2}=\frac{1}{u_1}-\frac{1}{u_2}\) = \(\frac{1}{u_1}-\frac{1}{u_1+f}\)
∴ \(1+\frac{v_1}{v_2}=\frac{fv_1}{u_1(u_1+f)}\)
∴ \(1+\frac{u_1}{u_1+f}=\frac{fv_1}{u_1(u_1+f)}\) …[from eq.(3)]
∴ \(\frac{2u_1+f}{u_1+f}=\frac{fv_1}{u_1(u_1+f)}\)
∴ 2u12 + fu1 = fv1
∴ \(\frac{2u_1^2}{u_1v_1f}+=\frac{fv_1}{u_1(u_1+f)}\)
∴ \(\frac{2u_1}{v_1f}+\frac{1}{v_1}=\frac{1}{u_1}\)
∴ \(\frac{2u_1}{v_1f}=\frac{1}{u_1}-\frac{1}{v_1}=\frac{1}{f}\) …[from eq.(1)]
∴ 2u1 = v1 , ∴ m1 = \(\frac{v_1}{u_1}\) = 2
\(\frac{h_1}{h_0}\) = 2 , ∴ h1 = 2h0 = 2(6 cm ) = 12 cm
The image size is 12 cm
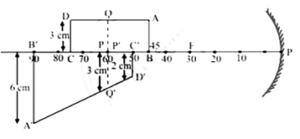
(vii) Figure below shows the section ABCD of a transparent slab. There is a tiny green LED light source at the bottom left corner B. A certain ray of light from B suffers total internal reflection at nearest point P on the surface AD and strikes the surface CD at point Q. Determine refractive index of the material of the slab and distance DQ. At Q, the ray PQ will suffer partial or total internal reflection? [You may use the approximation given in Q 1 above].
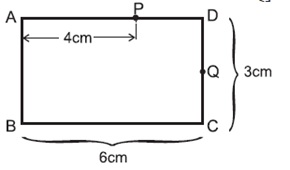
Given : AB = 3 cm, AP = 4 cm

BP = 5 cm (from the Pythagorean triad 3-4-5)
Since the ray BP suffers total internal reflection at P,
∠ BPE = iC (critical angle for the pair of mediums)
∴ sin iC = \(\frac{BE}{BP}=\frac{4}{5}\) = 0.8 …..(1)
∴ The refractive index of the material of the slab is
n = \(\frac{1}{sin\,i_C}\) =\(\frac{5}{4}\)
From Eq. (1), iC = sin—1 (0.8) = 53°8’
From the figure, the angle of incidence at Q is
i = 90° — iC = 90° — 53°8' = 36°52’
which is less than the critical angle for the pair of mediums. Hence the ray PQ will suffer partial internal reflection at Q.
(viii) A point object is kept 10 cm away from one of the surfaces of a thick double convex lens of refractive index 1.5 and radii of curvature 10 cm and 8 cm. Central thickness of the lens is 2 cm. Determine location of the final image considering paraxial rays only. Hint : Single spherical surface formula to be used twice.
Since the lens is thick, the thin lens equation cannot be applied. Refractions at the
two surfaces must be considered separately.
For the refraction at the first surface,
n1 = 1 (air), n2 = 1.5 (glass), u = − 10 cm,
image distance P1I1 = v’, R1 = 10 cm
\(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\)
∴ \(\frac{n_2}{v'}=\frac{n_2-n_1}{R_1}+\frac{n_1}{u}\)
∴ \(\frac{1.5}{v'}=\frac{1.5-1}{10}+\frac{1}{(-10)}=\frac{0.5}{10}-\frac{1}{10}=-\frac{1}{20}\)
∴ v’ = −1.5 × 20 = −30 cm
For the refraction at the Second surface,
the object distance u = P2I1 = P1I1 − P1P2 = −30 − 2 = −32 cm
image distance = v, R2 = − 8 cm, n1 = 1.5, n2 = 1
∴ \(\frac{n_2}{v}=\frac{n_2-n_1}{R_2}+\frac{n_1}{u}\)
∴ \(\frac{1}{v}=\frac{1-1.5}{-8}+\frac{1.5}{-32}=\frac{0.5}{32}=\frac{1}{64}\)
∴ v = 64 cm
Since v is positive, the final image is real.
∴ A real image is formed at 64 cm on the right hand side of the second surface.
(ix) A monochromatic ray of light is incident at 370 on an equilateral prism of refractive index 3/2. Determine angle of emergence and angle of deviation. If angle of prism is adjustable, what should its value be for emergent ray to be just possible for the same angle of incidence.
Given : i = 370, n = \(\frac{3}{2}\), A = 600
(i) n = \(\frac{sin\,i}{sin\,r_1}=\frac{sin\,e}{sin\,r_2}\)
∴ sin r1 = \(\frac{sin\,i}{n}=\frac{sin\,37^0}{3/2}=\frac{3}{2}\) × 0.6018 = 0.4012
∴ r1 = sin−1 0.4012 = 23033’
∴ r2 = A − r1 = 600 − 23033’ = 36027’
∴ sin e = n sin r2 = \(\frac{3}{2}\)sin 36027’ = \(\frac{3}{2}\)(0.5941) = 0.8912
The angle of emergence,
e = sin−1(0.8912) = 63°1'
The angle of deviation,
δ = i + e − A=37° + 63°1' − 60° = 40°1'
(ii) For just emergence, e = 90°.
In this case, sin r'2 = \(\frac{sin\,e}{n}=\frac{sin\,90^0}{3/2}=\frac{3}{2}\) = 0.6667
∴ r'2 = sin−1 (0.6667) = 41049’
∴ The angle of the prism for just emergence should be
= A’ = r1 + r'2 = 23°33’ + 41°49’ = 65°22’
Answer : e = 63°1', δ = 40°1', A = 65°22' for e = 90° (just emerges)
(x) From the given data set, determine angular dispersion by the prism and dispersive power of its material for extreme colours. nR = 1.62 nV = 1.66, δR = 3.1°
Given : nR = 1.62 nV = 1.66, δR = 3.1°
Since δR is small (<5°), the prism must be thin
For a thin prism, δV = A(nV — 1) and δR = A(nR — 1)
∴ \(\frac{δ_V}{δ_R}=\frac{n_V-1}{n_R-1}\) = \(\frac{1.66-1}{1.62-1}=\frac{0.66}{0.62}\)
∴ δV = 3.1° x \(\frac{33}{31}\) = 3.3°
∴ The angular dispersion,
δVR = δV — δR = 3.3° — 3.1° = 0.2°
The dispersive power,
ωVR = \(\frac{n_V-n_R}{\frac{n_V+n_R}{2}-1}\) = \(\frac{1.66-1.62}{\frac{1.66+1.62}{2}-1}\)
= \(\frac{0.04}{0.64}\) = 0.0625
Answer: δVR = 0.2°, ωVR = 0.0625
(xi) Refractive index of a flint glass varies from 1.60 to 1.66 for visible range. Radii of curvature of a thin convex lens are 10 cm and 15 cm. Calculate the chromatic aberration between extreme colours.
Given : ng = 1.60, nV = 1.66, R1 = 10 cm, R2 = -15 cm
\(\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})\)
∴ \(\frac{1}{f_R}=(1.6-1)(\frac{1}{10}-\frac{1}{15})=0.6(\frac{6+4}{60}) = \frac{1}{10}\)
∴ fR = 10 cm
\(\frac{1}{f_V}=(1.66-1)(\frac{1}{10}-\frac{1}{15})=0.66(\frac{6+4}{60}) = \frac{0.66}{6}\)= 0.11 cm
∴ fV = \(\frac{100}{11}\) cm
∴ the chromatic aberration between extreme colours,
fR - fV = \(10-\frac{100}{11}=\frac{110-100}{11}=\frac{10}{11}\) cm = 0.91 cm
(xii) A person uses spectacles of ‘number’ 2.00 for reading. Determine the range of magnifying power (angular magnification) possible. It is a concavoconvex lens (n = 1.5) having curvature of one of its surfaces to be 10 cm. Estimate that of the other.
Given : P = 2.00 D, n = 1.5, R1 =10 cm = 0.1 m D = 25 cm = 0.25 m
The minimum magnifying power,
Mmin = DP = (0.25)(2) = 0.5
The maximum magnifying power,
Mmax = 1 + DP = 1 + 0.5 = 1.5
By lens makers’ formula,
\(\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})\)
∴ \(\frac{1}{R_1}-\frac{1}{R_2}=\frac{1}{f(n-1)}=\frac{P}{n-1}=\frac{2}{1.5-1}=\frac{1}{0.25}\)
∴ (\frac{1}{R_2}= \frac{1}{R_1}-\frac{1}{0.25}\) = \(\frac{1}{0.1}-\frac{1}{0.25}\) = 10 – 4 = 6
∴ The radius of curvature of the other surface is
R2 = \(\frac{1}{6}\) m = (\frac{100}{6}\) cm ≈ 16.67 cm
Answer: Mmin = 0.5, Mmax = 1.5, R2 = 16.67 cm
(xiii) Focal power of the eye lens of a compound microscope is 6 dioptre. The microscope is to be used for maximum magnifying power (angular magnification) of at least 12.5. The packing instructions demand that length of the microscope should be 25 cm. Determine minimum focal power of the objective. How much will its radius of curvature be if it is a biconvex lens of n = 1.5.
Given : Pe = 6 D, M.P. = 12.5 (maximum), L = 25 cm, n = 1.5
Pe = 6D ∴ \(\frac{1}{f_e}\) = 6 m−1 = 0.06 cm−1
For maximum magnifying power, the final image is formed at the near point of the eye.
∴ ve = − 25 cm, ∴ \(\frac{1}{v_e}\) = − 0.04 cm−1
\(\frac{1}{f_e}=\frac{1}{v_e}-\frac{1}{u_e}\)
∴ \(\frac{1}{u_e}=\frac{1}{v_e}-\frac{1}{f_e}\) = −0.04 − (+0.06) = − 0.1 cm−1
∴ ue = −10 cm
v0 = L − |ue| = 25 – 10 = 15 cm …...(1)
M.P., Mmax = \(\frac{v_0}{|u_0|}\)(1 + PeD)
∴ \(\frac{v_0}{|u_0|}\)[1 + (6)(0.25)] = 12.5
∴ \(\frac{v_0}{|u_0|}\)(2.5) = 12.5
∴ \(\frac{v_0}{|u_0|}\) = 12.5/2.5 = 5
∴ |u0| = \(\frac{v_0}{5}\) = 3 cm …. From eq. (1)
∴ u0 =− 3 cm
\(\frac{1}{f_0}=\frac{1}{v_0}-\frac{1}{u_0}\) = \(\frac{1}{15}-\frac{1}{3}\)
= \(\frac{2}{5}\) cm−1 = \(\frac{200}{5}\) m−1
∴ The minimum focal power of the objective,
P0 = 200/5 = 40 D
For equiconvex lens
\(\frac{1}{f_0}\) = (n-1)\((\frac{2}{R})\)
∴ \(\frac{2}{5}\) cm−1 = (1.5 – 1)\((\frac{2}{R})\)
∴ \(\frac{2}{5}\) = \(\frac{1}{2}×\frac{2}{R})\)
∴ R = 5/2 = 2.5 cm
The radii of curvature of the equiconvex objective lens should be 2.5 cm.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 8: Sound – Online Solutions
Next Chapter : Chapter 10: Electrostatics – Online Solutions
We reply to valid query.