Magnetic Materials
Maharashtra Board-Class-12th-Physics-Chapter-11
Solutions
Question 1. Choose the correct option.
(i) Intensity of magnetic field of the earth at the point inside a hollow iron box is.
(A) less than that outside
(B) more than that outside
(C) same as that outside
(D) zero
(D) zero
(ii) Soft iron is used to make the core of transformer because of its
(A) low coercivity and low retentivity
(B) low coercivity and high retentivity
(C) high coercivity and high retentivity
(D) high coercivity and low retentivity
(A) low coercivity and low retentivity
(iii) Which of the following statements is correct for diamagnetic materials?
(A) μr < 1
(B) χ is negative and low
(C) χ does not depend on temperature
(D) All of above
(D) All of above
(iv) A rectangular magnet suspended freely has a period of oscillation equal to T. Now it is broken into two equal halves (each having half of the original length) and one piece is made to oscillate freely. Its period of oscillation is T′, the ratio of T′/T is…..
(A) \(\frac{1}{2\sqrt{2}}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(v) A magnetising field of 360 Am-1 produces a magnetic flux density (B) = 0.6 T in a ferromagnetic material. What is its permeability in TmA-1 ?
(A) 1/300
(B) 300
(C) 1/600
(D) 600
(C) 1/600
Question 2 Answer in brief.
(i) Which property of soft iron makes it useful for preparing electromagnet?
An electromagnet should become magnetic when a current is passed through its coil but should lose its magnetism once the current is switched off. Hence, the ferromagnetic core (usually iron-based) used for an electromagnet should have high permeability and low retentivity, i.e., it should be magnetically 'sofť.
(ii) What happens to a ferromagnetic material when its temperature increases above curie temperature?
- A ferromagnetic substance is made up of tiny sections called domains. Within each domain, the atomic magnetic moments of nearest-neighbor atoms interact strongly via exchange interaction, a quantum mechanical process, and align parallel to one another even in the absence of an external magnetic field. As a result, a domain becomes magnetically saturated on its own.
- The material preserves its domain structure only at a specific temperature. Heating causes greater thermal agitation, which acts against spontaneous domain magnetization. Finally, at a crucial temperature known as the Curie point or Curie temperature, thermal agitation overcomes exchange forces, allowing the atomic magnetic moments to remain randomly oriented. So, above the Curie point, the material becomes paramagnetic. The shift from ferromagnetic to paramagnetic is characterized by an increase in disorder. When cooled below the Curie point, the material regains its ferromagnetic properties.
(iii) What should be retentivity and coercivity of permanent magnet?
A permanent magnet should have a large zero-field magnetization and should need a very large reverse field to demagnetize. In other words, it should have a very broad hysteresis loop with high retentivity and very high coercivity.
(iv) Discuss the Curie law for paramagnetic material.
Curie’s law : The magnetization of a paramagnetic material is directly proportional to the external magnetic field and inversely proportional to the absolute temperature of the material.
If a paramagnetic material at an absolute temperature T is placed in an external magnetic field of induction the magnitude of its magnetization
Mz ∝ Bext/T, ∴ Mz = \(c\frac{B_{ext}}{T}\)
where the proportionality constant C is called the Curie constant.
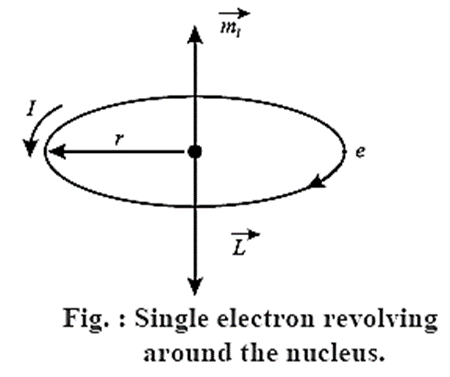
(v) Obtain and expression for orbital magnetic moment of an electron rotating about the nucleus in an atom.
In the Bohr model of a hydrogen atom, the electron of charge —e performs a uniform circular motion around the positively charged nucleus.
Let r, v and T be the orbital radius, speed and period of motion of the electron. Then,
T = 2πr/v …….(1)
Therefore, the orbital magnetic moment associated with this orbital current loop has a magnitude,
I = e/T = \(\frac{ev}{2πr}\)
Therefore, the magnetic dipole moment associated with this electronic current loop has a magnitude
M0 = current x area of the loop = I(πr2) = \(\frac{ev}{2πr}×πr^2\)=\(\frac{1}{2}evr\) ……..(3)
Multiplying and dividing the right hand side of the above expression by the electron mass me
M0 =\(\frac{e}{2m_e}(m_evr)\) = \(\frac{e}{2m_e}L_0\) …..(4)
where L0 = mevr is the magnitude of the orbital angular momentum of the electron. \(\vec{M_0}\) is opposite to \(\vec{L_0}\)
∴ \(\vec{M_0}\) = \(\frac{e}{2m_e}\vec{L_0}\) …..(5)
which is the required expression
According to Bohr’s second postulate of stationary orbits in his theory of hydrogen atom, the angular momentum of the electron in the nth stationary orbit is equal to \(n\frac{h}{2π}\) , where h is the Planck constant and n is a positive integer. Thus, for an orbital electron,
L0 = mev r = \(\frac{nh}{2π}\)
Substituting for L0 in Eq. (4),
M0 = \(\frac{enh}{4πm_e}\)
For n = 1 M0 = \(\frac{enh}{4πm_e}\)
The quantity \(\frac{enh}{4πm_e}\) is a fundamental constant called the Bohr magneton, μB.
μB = 9.274 x 10−24 I/T (or A-m2) = 5.788 x 10−5 eV/T.
(vi) What does the hysteresis loop represents?
A magnetic hysteresis loop is a closed curve obtained by plotting the magnetic flux density B of a ferromagnetic material against the corresponding magnetizing field H when the material is taken through a complete magnetizing cycle. The area enclosed by the loop represents the hysteresis loss per unit volume in taking the material through the magnetizing cycle.
(vii) Explain one application of electromagnet.
Applications of an electromagnet :
- Electromagnets are used in electric bells, loud speakers and circuit breakers.
- Large electromagnets are used in junkyard cranes and industrial cranes to lift iron scraps.
- Superconducting electromagnets are used in MRI and NMR machines, as well as in particle accelerators of cyclotron family.
- Electromagnets are used in data storage devices such as computer hard disks and magnetic tapes.
Question 3.
When a plate of magnetic material of size 10 cm × 0.5 cm × 0.2 cm (length , breadth and thickness respectively) is located in magnetising field of 0.5 × 104 Am-1 then a magnetic moment of 5 Am2 is induced in it. Find out magnetic induction in rod.
Given : l = 10 cm, b = 0.5 cm, h = 0.2 cm, H = 0.5 × 104 Am-1, M = 5 A.m2
The volume of the plate,
V = 10 × 0.5 × 0.2 = 1cm2 = 10-6 m2
B = μ0(H + Mz) = μ0 \((H+\frac{M}{V})\)
The magnetic induction in the plate,
∴ B = 4π x 10-7 \((0.5×10^4+\frac{5}{10^{-6}})\)
= 6.290 T
Question 4.
A rod of magnetic material of cross section 0.25 cm2 is located in 4000 A.m-1 magnetising field. Magnetic flux passing through the rod is 25 × 10−6 Wb. Find out
(a) relative permeability
(b) magnetic susceptibility and
(c) magnetisation of the rod
Given : A = 0.25 cm2 = 25 x 10-6 m2, H = 4000 A.m-1, ø = 25 x 10−6 Wb
Magnetic induction is
B = \(\frac{Φ}{A}\) = 1 Wb/m2
(a) Β = μ0μrΗ
∴ The relative permeability of the material,
μr = \(\frac{B}{μ_0H}\) = \(\frac{1}{4×3.142×10^{-7}×4000}\) = 198.9 = 199
(b) μr = 1 + χm
∴ The magnetic susceptibility of the material,
χm = μr – 1 = 199 – 1 = 198
(c) χm = \(\frac{M_z}{H}\)
The magnetization of the rod,
Mz = χmH = 198 x 4000 = 7.92 × 105 A/m
Question 5.
The work done for rotating a magnet with magnetic dipole moment m, through 90° from its magnetic meridian is n times the work done to rotate it through 60°. Find the value of n.
Given : θ0 = 0°, θ1 = 90°, θ2 = 60°, W1 = nW2
The work done by an external agent to rotate the magnet from 00 to 0 is
W = MB (cos θ0 - cos θ)
∴ W1 = MB (cos θ0 - cos θ1)
= MB (cos 0° - cos 90°)
= MB (1 - 0)
= MB
∴ W2 = MB (cos 0° - cos 60°)
= MB
= 0.5 MB
∴ W1 = 2W2 = MB
Given W1 = nW2 . Therefore n = 2
Question 6.
An electron in an atom is revolving round the nucleus in a circular orbit of radius 5.3 × 10−11 m, with a speed of 2 × 106 m/s. Find the resultant orbital magnetic moment and angular momentum of electron. (charge on electron e = 1.6 × 10−19 C, mass of electron m = 9.1 × 10−31 kg.)
Given : r = 5.3 x 10−11 m, v = 2 x 106 m/s, e = 1.6 x 10−19 C, me = 9.1 x 10−31 kg
The orbital magnetic moment of the electron is
M0 = \(\frac{1}{2}\)evr
= \(\frac{1}{2}\)(1.6 x 10−19) (2 x 106) (5.3 × 10−11)
= 8.48 x 10−24 A.m2
The angular momentum of the electron is
L0 = mevr
= (9.1 × 10−31)(2 × 106)( 5.3 × 10−11)
= 96.46 × 10−36 = 9.646 × 10−35 kg-m2/s
Question 7.
A paramagnetic gas has 2.0 × 1026 atoms/m with atomic magnetic dipole moment of 1.5 × 10−23 A m2 each. The gas is at 27° C. (a) Find the maximum magnetization intensity of this sample. (b) If the gas in this problem is kept in a uniform magnetic field of 3 T, is it possible to achieve saturation magnetization? Why?
(Hint: Find the ratio of Thermal energy of atom of a gas ( 3/2 kBT) and maximum potential energy of the atom (mB) and draw your conclusion)
Given : \(\frac{N}{V}\) = 2.0 × 1026 atoms/m3,
μ = 1.5 × 10-23 A.m2, T = 27 + 273 = 300 K, B = 3 T, kB = 1.38 × 10-23 J/K,
1 eV = 1.6 × 10-19 J
(a) The maximum magnetization of the material,
MZ = \(\frac{N}{V}\)μ = (2.0 × 1026)(1.5 × 10-23) = =3 × 103 A/m
(b) The maximum orientation energy per atom is
Umax = −μB cos 180° = μB
= (1.5 × 10-23)(3) = 4.5 × 10-23 J = eV = 2.8 × 10-4 eV
The average thermal energy of each atom,
E = \(\frac{3}{2}\)kBT
where kB is the Botzmann constant.
∴ E = 1.5(1.38 x 10−23)(300)
= 6.21 x 10−21 J = \(\frac{6.21×10^{-21}}{1.6×10^{-19}}\) eV = 3.9 × 10−2 eV
Since the thermal energy of randomization is about two orders of magnitude greater than the magnetic potential energy of orientation, saturation magnetization will not be achieved at 300 K.
Question 8.
A magnetic needle placed in uniform magnetic field has magnetic moment of 2 × 10-2 A.m2, and moment of inertia of 7.2 × 10-7 kg m2. It performs 10 complete oscillations in 6 s. What is the magnitude of the magnetic field ?
Given : M = 2 × 10−2 A.m2, I = 7.2 × 10−7 kg m2, T = 6/10 = 0.6 s
T = 2π\(\sqrt{\frac{I}{MB}}\)
The magnitude of the magnetic field is
B = \(\frac{4π^2I}{MT^2}\) = \(\frac{(4)(3.14)^2(7.2×10^{-7}}{(2×10^{-2})(0.6)^2}\) = 3.943 × 10−3T = 3.943 mT
Question 9.
A short bar magnet is placed in an external magnetic field of 700 guass. When its axis makes an angle of 30° with the external magnetic field, it experiences a torque of 0.014 Nm. Find the magnetic moment of the magnet, and the work done in moving it from its most stable to most unstable position.
Given : B = 700 gauss = 0.07 tesla, θ = 30°, τ = 0.014 N·m,
τ = MB sin θ
The magnetic moment of the magnet is
M = \(\frac{τ}{B\,sin\,θ}=\frac{0.014}{(0.07)(sin\,30^0)}\) = 0.4 A.m2
The most stable state of the bar magnet is for θ = 0°.
It is in the most unstable state when θ = 180°.
Thus, the work done in moving the bar magnet from 0° to 180° is
W = MB (cos θ0 − cos θ)
= MB (cos 0° − cos 180°)
= MB [1 − (−1)]
= 2MB = (2)(0.4)(0.07)
= 0.056 J
This the required work done.
Question 10.
A magnetic needle is suspended freely so that it can rotate freely in the magnetic meridian. In order to keep it in the horizontal position, a weight of 0.2 g is kept on one end of the needle. If the pole strength of this needle is 20 Am , find the value of the vertical component of the earth's magnetic field. (g = 9.8 m/s2)
Given : M = 0.2 g = 2 × 10−4 kg, qm = 20 A·m, g = 9.8 m/s2
Without the added weight at one end, the needle will dip in the direction of the resultant magnetic field inclined with the horizontal. The torque due to the added weight about the vertical axis through the centre balances the torque of the couple due to the vertical component of the Earth's magnetic field.
∴ (Mg)\(\frac{L}{2}\) = (qm Bv)L
The vertical component of the Earth's magnetic field,
Bv = \(\frac{Mg}{2q_m}\) = \(\frac{2×10^{-4}×9.8}{2×20}\) = 4.9 × 10−5 T
Question 11.
The susceptibility of a paramagnetic material is χ at 27° C. At what temperature its susceptibility be χ/3 ?
Given : χm1 = χ T1 = 27 0C = 300 K, χm2 =
By Curie's law,
Mz = \(C\frac{B_0}{T}\)
Since Mz = χmH and B0 = μ0H
χmH = \(C\frac{μ_0H}{T}\)
∴ χm = \(C\frac{μ_0}{T}\)
∴ χm ∝ \(\frac{1}{T}\)
∴ \(\frac{χ_{m1}}{χ_{m2}}\) = \(\frac{1}{T}\)
∴ T2 = \(\frac{χ_{m1}}{χ_{m2}}\)×T1 = 3\(\frac{χ}{χ}\) x 300 = 900 K = 627°C
This gives the required temperature.
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-10-Magnetic Fields due to Electric Current –Online Solution Next Chapter :Chapter-12- Electromagnetic Inductions – Online Solution
We reply to valid query.