Gravitation
Maharashtra Board-Class-11-Science-Physics-Chapter-5
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction:
- Everybody's bodies are drawn to the Earth with a constant acceleration.
- The phenomenon that keeps planets in their orbits around the Sun is gravity. Due to gravity, the moon likewise rotates around the Earth.
- Every massive object in the universe experiences gravitational force. It is the force of attraction that any two objects have to one another as a result of their relative masses.
- It is a constant force of attraction with limitless potential. It is independent of any intermediary medium.
- Compared to other fundamental forces, it is much weaker. Gravitational force is 10-39 times weaker than strong nuclear force.
Kepler’s Laws:
Kepler analysed the huge data meticulously recorded by Tycho Brahe and established three laws of planetary motion.
(1) Law of orbits : All planets move in elliptical orbits around the Sun with the Sun at one focus of the ellipse.
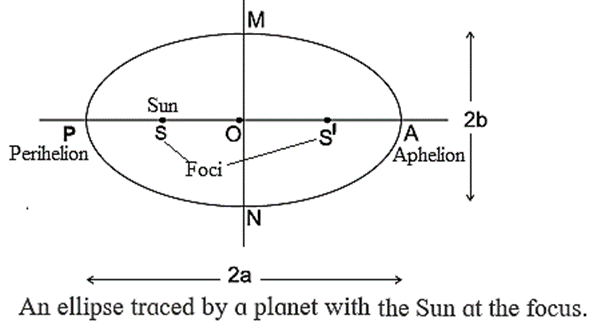
The orbit of a planet around the Sun is shown in below Fig.
- S, S′ = foci of the ellipse. Sun at S.
- P = Perihelion- Closest point along the orbit from S
- A = Aphelion - Farthest point from S .
- PA = Major axis = 2a. PO, AO = Semimajor axes = a.
- MN = Minor axis =2b.MO, ON = Semiminor axes = b
(2) Law of areas : The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
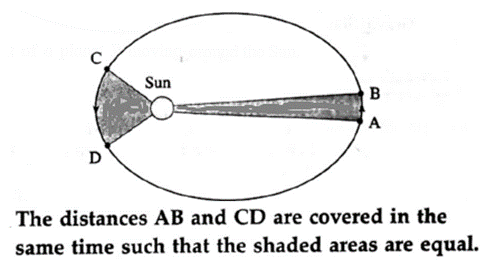
Proof :
Assume that the force exerted on a planet by the Sun is a central force. Kepler ’s law of areas is a consequence of conservation of angular momentum.

Let P be a planet in an elliptical orbit with the Sun S at one of the foci of the ellipse. Let m be the mass of the planet, \(\vec{r}\) be the position vector of the planet with respect to the Sun, \(\vec{v}\) be the velocity of the planet and \(\vec{p}\) be the momentum of the planet (see above fig ).
\(\vec{p}\) = \(m\vec{v}\) , ∴ \(\vec{v}= \frac{\vec{p}}{m}\) ...(l)
Angular momentum of the planet,
\(\vec{L}=\vec{r}×\vec{p}\) ...(2)
Let ΔA be the area swept out by the planet in space in time interval Δt.
ΔA = \(\frac{1}{2}|\vec{r}×\vec{v}Δt|\)
∴ The time rate of change of area,
\(\frac{ΔA}{Δt}\) = \(\frac{1}{2}|\vec{r}×\vec{v}|\)
= \(\frac{1}{2}(\vec{r}×\frac{\vec{p}}{m})\)
= \(\frac{1}{2m}(\vec{r}×\vec{p})\)
∴\(\frac{ΔA}{Δt}\) = \(|\frac{\vec{L}}{2m}|\)
The angular momentum is conserved for a central force. As the angular momentum and mass of the planet remain constant, the quantity \(\frac{\vec{L}}{2m}\) remains constant.
∴ \(\frac{ΔA}{Δt}\) = \(\frac{\vec{L}}{2m}\) = constant …. (4)
which proves Kepler's law of areas.
(3) Law of periods : The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
If r is length of semimajor axis then, this law states that
T2 ∝ r3
Or
T2/r3 = constant
Universal Law of Gravitation:
Newton's law of universal gravitation : Every particle of matter in the universe attracts every other particle with a force which is directly proportional to the product of their masses, inversely proportional to the square of the distance between them and acts along the line joining them.

The force on particle 2 by particle 1 is \(\vec{F}_{21}\) . The force on particle 1 by particle 2 is \(\vec{F}_{12}\)
\(\vec{F}_{12}\) = \(−\vec{F}_{21}\) . The forces and equal in magnitude and opposite in direction, form the action-reaction pair.
Gravitational constant :
According to Newton's law of universal gravitation, the force of attraction between two particles is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
F ∝ m1m2/r2 ∴ F = \(G\frac{m_1m_2}{r^2}\)
The constant of proportionality G is called gravitational constant. It is a universal constant. The order of magnitude of G is 10−10 N.m2/Kg2 which makes the gravitational force a very weak force.
SI unit of G : \(\frac{newton(metre)^2}{(kilogram)^2}\) or N.m2/Kg2 .
CGS unit of G : \(\frac{dyne(centimetre)^2}{(gram)^2}\) or dyn.cm2/g2
Dimensions of G :
[G]= \(\frac{[F][r^2]}{[m_1m_2]}\) =\(\frac{[M^1L^1T^{-2}][M^0L^2T^0]}{[M^2L^0T^0]}\) = [M—1L3T—2]
Centripetal acceleration of the Moon :
It was known that the moon completes one revolution about the Earth in 27.3 days. The distance from the Earth to the moon is 3.85 × 105 km.
The Moon revolves around the Earth in almost a circular orbit with constant angular speed ω. If m is the mass of the Moon, r is the distance from the centre of the Moon to the centre of the Earth, the centripetal force F acting on the Moon is given by;
F = mω2r ……(1)
According to Newton's second law of motion, we have :
F = m a ….(2)
From (1) and (2), we get :
ma = mω2r
∴ a = ω2r ….(3)
∴ a = \((\frac{2π}{T})^2r\) ...(as ω = 2π/T)……(4)
Substituting the values of r and T, the centripetal acceleration of the Moon is
a = \(\frac{4π^2(3.85×10^8)}{(27.3×8.64×10^4)^2}\)
∴ a = 0.0027 m/s2 = 2.7 x 10−3 m/s2
This is the acceleration of the moon which is towards the centre of the Earth, i.e., centre of orbit in which the moon revolves.
Q. How did Newton use the motion of the Moon around the Earth to test his universal law of gravitation :
By using an analytical approach, Newton had demonstrated that if a body's route is a conic section, it must be subject to a central force, and that the magnitude of the force must be inversely proportional to the square of the distance of the body from the conic section's centre (the inverse square law).
The force that keeps a planet in its orbit is of the same nature as that of the force of gravity at the surface of the Earth, he suggested, and the same natural results must be attributed to the same sources (the principle of universal gravitation).
Consequently, to test his inverse square law, Newton extended the Earth's gravity to the orbit of the Moon and compared the centripetal acceleration of the Moon (aM) with the acceleration due to gravity near the Earth's surface (g). He assumed the Moon to be in a nearly circular orbit around the Earth and that the acceleration due to the Earth's gravity at the Moon's orbit provides exactly the correct amount of centripetal acceleration to keep the Moon in orbit.
Let r, vM and T be the orbital radius, speed and period of the Moon, and RE be the radius of the Earth. Then,
vM = 2πr/T and aM = vM2 /r = 4π2r/T2 ....(1)
Also, it follows from the inverse square law,
g/aM = (r/RE)2 ....(2)
In Newton's days the following values were known :
g = 32 ft/s2, RE ≈ 4000 miles, r ≈ 60RE, T ≈ 27 days.
On converting to SI units, using
1 ft ≈ 0.305 m and 1 mi = 1.60 km, g = 9.76 m/s2 and RE ≈ 6400 km
From Eq. (1), aM = 2.786 x 10−3 m/s2 and
g/aM = \(\frac{9.76}{2.78×10^3}\) = 3503
and from Eq. (2), g/aM = (r/RE)2 = (60)2 = 3600
which was a remarkable agreement, keeping in mind that the Moon's orbit is slightly elliptical and that the above values are only approximate.
[Note : The gravitational force of the Earth on the Moon could not be determined because their masses and the gravitational constant were not known in Newton's days.]
Know This :
- The gravitational force on a particle inside any hollow closed object is zero.
- The gravitational force of attraction between a hollow spherical shell or solid sphere of uniform density and a point mass situated outside is just as if the entire mass of the shell or sphere is concentrated at the centre of the shell or sphere.
- The value of acceleration due to gravity can be assumed to be constant when we are dealing with objects close to the surface of the Earth. This is because the difference in their distances from the centre of the Earth is negligible.
Measurement of the Gravitational Constant (G):
The magnitude of the gravitational constant G can be found by measuring the force of gravitational attraction between two bodies of masses m1 and m2 separated by certain distance ‘L’. This can be measured by using the Cavendish balance.
Structure and working of the Cavendish balance :
The Cavendish torsion balance has a light rigid rod, of length L, suspended horizontally by a thin wire about 100 cm long.
Two small lead spheres s1 and s2 — each of mass m and diameter 5 cm — are attached at the two ends of the rod.
Two large lead spheres 1 and 2 — each of mass M and diameter 20 cm — are brought close to the small spheres and on opposite sides of the rod.

The mutual gravitational attraction between 1 and s1 and between 2 and s2 exerts a deflecting torque on the rod and causes the vertical suspension wire to twist by a measurable amount.
Due to the elastic property of the wire, the twisted wire exerts a restoring torque on the rod tending it to turn in the opposite sense.
The rod stops turning when the restoring torque equals the deflecting torque in magnitude.
If r is the initial distance between the centre of a large sphere and the small sphere near to it, then the magnitude of the gravitational form between them,
F = \(\frac{GMm}{r^2}\) ….(1)
The magnitude of the deflecting torque is
τ = FL = \(\frac{GMm}{r^2}L\) ...(2)
The restoring torque produced in the wire is Kθ, where K is the restoring torque per unit angle and θ is the angle of twist.
At equilibrium,
\(\frac{GMm}{r^2}L\) = Kθ ……(3)
The angle θ is measured with a beam of light reflected from a small mirror fixed to the suspension wire. The reflected beam is observed on a ground-glass scale, the light beam serving as a weightless pointer.
Thus, from the measured values of m, M, L, r and θ, the value of gravitational constant G can be calculated using Eq. (3).
Acceleration due to Gravity:
Consider a body of mass m on the surface of the Earth. By definition, the weight of the body is the gravitational force exerted on it by the Earth, so that
Fg = mg ….(1)
where g is the acceleration due to gravity on the surface of the Earth.
By Newton's law of gravitation,
Fg = \(\frac{GMm}{R^2}\) …..(2)
where G is the universal gravitational constant, M is the mass of the Earth and
R ≡ radius of the Earth is the distance between the centre of the Earth and the body.
From Eqs. (1) and (2),
mg = \(\frac{GMm}{R^2}\)
∴ g = \(\frac{GM}{R^2}\) ……(3)
This is the required relation.
| Know This :
An object of mass m (much smaller than the mass of the Earth) is attracted towards the Earth and falls on it. The Earth is also attracted by the same force (magnitude) toward the mass m. However, its acceleration towards m will be aEarth = \(\frac{\frac{GMm}{r^2}}{M}\) = \(\frac{Gm}{r^2}\) ∴ aEarth /g = \(\frac{Gm}{r^2}\)/\(\frac{GM}{r^2}\) = \(\frac{m}{M}\) .... (as g = \(\frac{GM}{r^2}\) ) As m << M, aEarth<< g and is nearly zero. Thus, practically only the mass m moves towards the Earth. |
Variation in the Acceleration due to Gravity with Altitude, Depth, Latitude and Shape:
(A) Variation in g with Altitude:
The acceleration due to gravity on the Earth’s surface is given by,
g = \(\frac{GM}{R^2}\) ….(1)
Here M and R is the mass and radius of the Earth, g is the acceleration due to gravity at the Earth's surface and G the gravitational constant.

Consider a body of mass m at an altitude h above the Earth’s surface. Then, its distance from the centre of the Earth is R + h. If gh is the acceleration due to gravity at the altitude h. Then, the weight of the body there is mgh and the gravitational force acting on it is
Fg = \(\frac{GMm}{(R+h)^2}\) ∴ mgh = \(\frac{GMm}{(R+h)^2}\)
∴ gh = \(\frac{GM}{(R+h)^2}\) ….(1)
Dividing Eq. (2) by Eq. (1), we get;
∴ gh = \(\frac{R^2}{(R+h)^2}\) = \(g(\frac{R}{(R+h)})^2\) ……(3)
This is the expression for the gravitational acceleration at an altitude h.
For low altitudes, i.e. for h/R << 1, we can write
gh = \(g(\frac{R+h}{R})^{-2}\) = \(g(1+\frac{h}{R})^{-2}\)
Expanding the bracketed term on the right hand side and retaining only the first order term,
∴ gh = \(g(1-\frac{2h}{R})\) …[….as (1+x)−2 = 1 − 2x + 3x2 − 4x3]
This equation shows that, the acceleration due to gravity gh goes on decreasing with increase in altitude of body from the surface of the Earth.
(B) Variation in g with Depth:
The acceleration due to gravity on the Earth’s surface is given by,
g = \(\frac{GM}{R^2}\) ….(1)
Here M and R is the mass and radius of the Earth, g is the acceleration due to gravity at the Earth's surface and G the gravitational constant.
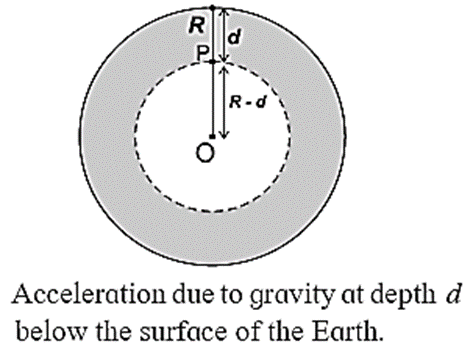
Let the Earth be a solid sphere with uniform density.
Density (ρ) = \(\frac{mass(M)}{volume(V)}\) = \(\frac{M}{\frac{4}{3}πR^3}\)
∴ M = \(\frac{4}{3}πR^3ρ\)
Thus, Eq. (1) becomes
g = \(\frac{G}{R^2}×\frac{4}{3}πR^3ρ\) = \(\frac{4}{3}πRρG\) ….(2)
Consider a body of mass m at a depth d below the Earth's surface. Then, its distance from the Earth's centre is R − d. Let gd be the acceleration due to gravity at the depth d. Then,
gd = \(\frac{GM'}{(R-d)^2}\) …..(3)
Where M’ = volume of the inner sphere x density
M’ = \(\frac{4}{3}π(R-d)^3ρ\)
Thus, Eq. (3) becomes
gd = \(\frac{\frac{4}{3}π(R-d)^3ρG}{(R-d)^2}\)
∴ gd = \(\frac{4}{3}π(R-d)ρG\) …..(4)
Dividing Eq. (4) by Eq. (2), we get
\(\frac{g_d}{g}\) = \(\frac{\frac{4}{3}π(R-d)ρG}{\frac{4}{3}πRρG}\)
∴ gd = \(g(1-\frac{d}{R})\) ….(5)
This is the required expression.
The expression shows that gd decreases with increasing depth. At the centre of the Earth, d = R, gd = 0
Hence, a body of mass m if taken to the centre of Earth, will not experience the force of gravity due to the Earth.
Conclusion :
Thus, the value of acceleration due to gravity is maximum at the surface of the Earth. The value goes on decreasing with
1) increase in depth below the Earth’s surface. (varies linearly with (R-d) = r)
2) increase in height above the Earth’s surface. (varies inversely with (R+h)2 = r2)
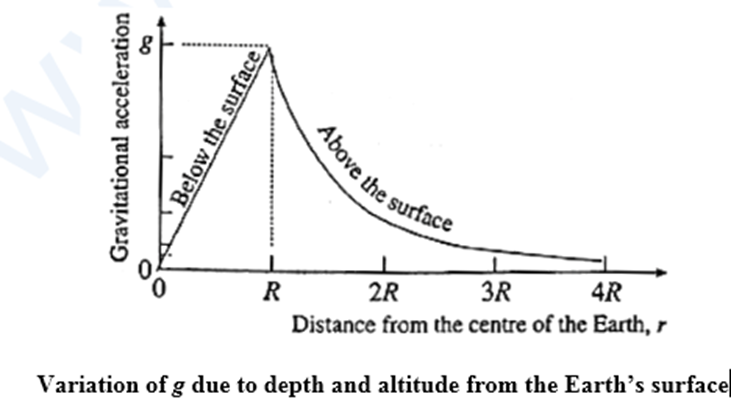
Graphically the variation of acceleration due to gravity according to depth and height can be expressed as follows.
Graph of the variation of gravitational acceleration due to the depth and altitude from the Earth's surface :
The expressions for the gravitational acceleration at a depth d and at an altitude h are, respectively,
gd = \(g(1-\frac{d}{R})=g(\frac{r}{R})\) …. (1)
and gh = \(g(\frac{R}{R+h})^2=g(\frac{R}{r})^2\) …. (2)
where R is the radius of the Earth, and r is the distance from the centre of the Earth. In Eq. (1) r = R−d, while in Eq.(2) r = R+h.
Using these expressions, the values of gd and gh for a few values of r are tabulated below.
| r = R−d | gd | r = R+h | gh |
| 0 | 0 | R | g |
| R/4 | g/4 | 2R | g/4 |
| R/2 | g/2 | 3R | g/9 |
| R | g | 4R | g/16 |
Using the values in the table we can plot the graph of g versus r.
(C) Variation in g with Latitude and Rotation of the Earth:
Latitude is an angle made by radius vector of any point from centre of the Earth with the equatorial plane. Obviously it ranges from 00 at the equator to 900 at the poles.
The Earth rotates about its polar axis from west to east with uniform angular velocity ω. Hence every point on the surface of the Earth (except the poles) moves in a circle parallel to the equator.
Expression : Consider a body of mass m at point P on the Earth's surface. The latitude of P is θ. The body is at a distance R from the centre of the Earth, where R is the radius of the Earth. As the Earth rotates about its axis, the body performs uniform circular motion with a radius r and angular speed ω. ∠ EOP, ∠ OPO’ = θ In Δ OPO’, cos θ = PO’/PO = r/R ∴ r = R cos θ The centripetal acceleration of the body directed along PO’ has a magnitude a = ω2r = ω2R cos θ ...(1) Its component towards the centre of the Earth (i.e., along PO) is ar = a cos θ = ω2R cos θ.cos θ = ω2R cos2θ …..(2) Now, the effective acceleration g’ due to gravity at P directed towards the centre of the Earth is, g’ = (gravitational acceleration) − (component of centrifugal acceleration) = g − ar = g − ω2R cos2θ This is the required expression

Effective acceleration due to gravity at equator and poles :
At the equator θ = 0°
cos θ = cos 0°= 1
Now, ω = 2π/T where T is the time taken by the Earth to complete one rotation about its axis.
∴ ω = \(\frac{2×3.14}{24×60×60}\) = 7.27 x 10−5 s−1
g’ = g − (7.27 x 10−5)2 (6.4 x 106) ….[Radius of the Earth = 6.4 x 106 m]
= g − 0.0338 m/s2
This means that, the effective acceleration due to gravity at the equator is minimum.
At the poles θ = 90°
cos θ = cos 90° = 0O
.'.g’ = g − ω2R cos2θ = g − 0
g' = g
This means that, the effective acceleration due to gravity at the poles is maximum.
There is no reduction in acceleration due to gravity at poles, due to the rotation of the Earth as the poles are lying on the axis of rotation and do not revolve.
Effect of the shape of the Earth:
(i) Effect on acceleration : The gravitational acceleration is maximum at the poles.
The gravitational acceleration on the Earth's surface is g g = GM/R2, where G, M and R are respectively the universal gravitational constant, mass of the Earth and radius of the Earth.
The equatorial radius of the Earth is bigger than the polar radius because it is an oblate spheroid with an equatorial bulge. The gravitational acceleration also varies with latitude as a result of the planet's rotation around its axis. g on the surface of the Earth is minimum near the equator and largest at the poles as a result of the combined impacts of these two forces.
(ii) Effect on weight :
Weight of an object is the force with which the Earth attracts that object. Thus, weight W = mg where m is the mass of the object. As the value of g changes with altitude, depth and latitude, the weight also changes. Weight of an object is minimum at the equator. Similarly, the weight of an object reduces with increasing height above the Earth’s surface and with increasing depth below the its surface.
Variation of the weight of an object due to variation in the gravitational acceleration :
The weight of an object is the force with which the Earth attracts that object. If m is the mass of an object and g is the gravitational acceleration, the weight W of the object is
W = mg
(a) Above / below the Earth's surface :
- If an object is raised to an altitude h above the Earth's surface, the gravitational acceleration decreases and hence the weight of the object reduces.
- If an object is taken to a depth d below the Earth's surface, the gravitational acceleration decreases and hence the weight of the object reduces.
(b) On the Earth's surface :
- The gravitational acceleration at the equator is minimum and hence the weight of the object there is also minimum.
- The gravitational acceleration is maximum at the poles and hence the weight of the object there is also maximum.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 4: Laws of Motion – Online Notes
Next Chapter : Chapter 6: Mechanical Properties of Solids – Online Notes
Notes are so helpful thank you so much for your support 😊