Gravitation
Maharashtra Board-Class-11-Science-Physics-Chapter-5
Notes-Part-2
Topics to be Learn : Part-2
|
Gravitational Potential and Potential Energy:
Potential energy : Potential energy is the work done against a conservative force in achieving a certain position or configuration of a given system.
Gravitational potential : The gravitational potential at a point in a gravitational field is defined as the work done per unit mass to bring a particle from infinity to that point, the work being done by an external agent against the gravitational force on particle, keeping the particle in equilibrium.
Gravitational potential energy : Gravitational potential energy of a particle is defined as the work done by an external agent in bringing the particle from infinity to a given point against the gravitational force, keeping the particle in equilibrium.
Expression for Gravitational Potential Energy:
The gravitational force due to the Earth on a body of mass m is
\(\vec{F}_g=-\frac{GM_Em}{r^2}\hat{r}\)
where G is the universal gravitational constant, ME is the mass of the Earth, r is the distance of the body from the centre of the Earth and \(\hat{r}\) the unit vector in the direction of \(\vec{r}\)

If \(\vec{F}_{ext}\) is the force exerted by an external agent to move the body against the gravitational force, keeping it in equilibrium at every instant,
\(\vec{F}_{ext}\) = \(\vec{F}_g\)
The infinitesimal work dW done by the external agent for the displacement \(d\vec{r}\) is
dW = (\vec{F}_{ext}.(d\vec{r}\)
= \(-(-\frac{GM_Em}{r^2}\hat{r}).d\vec{r}\)
= \(\frac{GM_Em}{r^2}.dr\)
The total work done by the external agent in moving the body from P(\(\vec{r}\)) to Q(\(\vec{r}\)) is,
W = \(\int_{r_i}^{r_f}\frac{GM_Em}{r^2}.dr\) = \(-GM_Em(\frac{1}{r_f}-\frac{1}{r_i})\)
Change in potential energy corresponds to the work done against conservative forces :
The change in potential energy is the work done by the external agent.
.'.W = ΔU = Uf − Ui
Choosing Ui = 0 for ri = ∞
Uf = \(-\frac{GM_Em}{r_f}\)
We usually drop the subscript f, so that at a distance r from the centre of the Earth, the gravitational potential energy of the Earth—body system is
U = \(-\frac{GM_Em}{r}\)
This is the required expression.
Connection of potential energy formula with mgh :
When a body of mass m is on the surface of the Earth of mass M and radius R, the gravitational potential energy of the system is
U1 = \(-\frac{GMm}{R}\) …..(1)
When the body is lifted to an altitude h, r = R + h and the gravitational potential energy is,
U2 = \(-\frac{GMm}{R+h}\) …..(2)
The increase in the potential energy;
ΔU = U2 − U1
= \(-\frac{GMm}{R+h}-(-\frac{GMm}{R})\)
= \(GMm[-\frac{1}{R+h}-(-\frac{1}{R})]\)
= \(GMm[\frac{h}{R(R+h)}]\) = \(\frac{GMmh}{R(R+h)}\)
If g is the acceleration due to gravity on the surface of the Earth,
g = GM/R2 ∴ GM = gR2
∴ ΔU = \(\frac{gR^2mh}{R(R+h)}\) = \(mgh(\frac{R}{R+h})\)
For h << R, R + h ≅ R
∴ ΔU = mgh
This is the required expression
Thus, mgh is increase in the gravitational potential energy of the Earth -mass system if an object of mass m is lifted to a height h, provided h is negligible compared to radius of the Earth (up to a few kilometers).
Concept of Potential:
The gravitational potential at a point at a distance r from a point mass M is
V = −GM/r
where G is the constant of gravitation.
If a particle of mass m is placed in a gravitational field at a point where the gravitational potential is V, the gravitational potential energy of the particle is
PE = mass x gravitational potential
= mV = − GMm/r
Escape speed : The minimum speed with which a body should be projected from the surface of the Earth so that it escapes the Earth's gravitational field is called the escape speed of the body.
Consider a body of mass m projected from the Earth's surface with escape speed ve.
The kinetic and potential energies of the body, just after throwing it,
KE = \(\frac{1}{2}\)mve2
PE = − GMm/R
where G is the gravitational constant, M is the mass of the Earth and R is the radius of the Earth.
Thus, the total energy of the object just after projection,
= KE + PE
= \(\frac{1}{2}\)mve2 − GMm/R …..(1)
Under the Earth's gravitational pull, the speed of the body decreases with time. So, when the body reaches infinity, its speed becomes zero.
Thus, kinetic and potential energies of the body at infinity,
KE = 0
PE = − GMm/∞ = 0
Thus, the total energy of the body at infinity,
= KE + PE = 0 ……(2)
As the total energy is conserved,
\(\frac{1}{2}\)mve2 − GMm/R = 0
∴ \(\frac{1}{2}\)mve2 = GMm/R
∴ ve = \(\sqrt{\frac{2GM}{R}}\)
This is the required expression.
- Thus, the escape speed is independent of the mass of the body and the direction of projection.
- It depends on the gravitational potential at the point of launching. Since this potential depends slightly on the latitude and height of the point, the escape speed depends slightly on these factors.
If m is the mass of the body, its weight mg is the gravitational force on it by the Earth.
∴ mg = GMm/R2 ∴ GM = gR2
Substituting this value in the expression ve = \(\sqrt{\frac{2GM}{R}}\) we get,
∴ ve = \(\sqrt{\frac{2gR^2}{R}}\) = \(\sqrt{2gR}\)
If ρ is the density of the Earth
Density = \(\frac{mass}{volume}\) ∴ ρ = \(\frac{M}{\frac{4}{3}πR^3}\)
∴ M = \(\frac{4}{3}πR^3ρ\)
Escape speed, ve = \(\sqrt{\frac{2GM}{R}}\)
∴ ve = \(\sqrt{\frac{2G}{R}×\frac{4}{3}πR^3ρ}\) = = \(2R\sqrt{\frac{2πρG}{3}}\)
Earth Satellites:
An Earth satellite is a body which revolves around the Earth in a circular or elliptical orbit under the influence of the Earth's gravitational attraction.
Artificial satellite : A man-made satellite that revolves around the Earth in a circular or elliptical path is called an artificial satellite.
Geostationary satellite :
- A geostationary satellite is a man-made satellite that has been propelled into a circular orbit around the Earth in the equatorial plane, rotating at the same rate as the planet.
- The orbital period of a geostationary satellite is equal to the rotational period of the earth.
- Above a specific geographic longitude, it looks stationary because its revolution is synchronised with the Earth's rotation.
- It is also known as a geosynchronous satellite because of this.
Communication satellite :
- These are geostationary satellites. They revolve around the Earth in equatorial plane
- Up to 76° latitude above and below the equator, a geostationary satellite with radio transponders receives radio signals from a transmitting station and broadcasts them back to Earth.
- Three such satellites uniformly spaced in a geosynchronous orbit provide global communication. Such a satellite is called a communication satellite or Synchronous Communication Satellite (acronym SYNCOMS).
Applications of a communication satellite :
These are used for,
- Telephones and radio wave signal transmission
- Communication of TV signals over a large distance on Earth's surface
- Geological survey
- Weather forecasting
- e.g., INSAT group of satellites launched by India.
Polar satellite : A polar satellite is an artificial satellite in a low-altitude orbit (altitude about 500 km to 800 km), which passes over the poles of the Earth.
Uses of a polar satellite :
- Geological survey
- Telecommunications
- Global positioning system (GPS)
- Astronomical observations, study of solar radiation.
Projection of Satellite:
For the projection of an artificial satellite, it is necessary for the satellite to have a certain velocity and a minimum two stage rocket.
Launching of artificial satellite :
- An artificial satellite is launched by a launch vehicle consisting of a multistage rocket of at least two stages.
- The satellite is mounted in a capsule atop the launch vehicle.
- A rocket is a reaction engine whose basic driving principle is Newton's third law of motion.
- Hot gases of the burning fuel mix leave the rocket at very high speed in the downward direction. The reaction of this ejecting gas propels the satellite and the launch vehicle vertically up.
- When a two—stage rocket is used, the first-stage is used to provide a high initial thrust straight up which gets the satellite through the thickest part of the atmosphere to the desired altitude.
- The empty first-stage is detached and the remaining launch vehicle is rotated through 90°. Then, a controlled and lower thrust by the second-stage imparts the correct horizontal velocity, called the critical velocity, to the satellite to put it into a stable circular orbit. This velocity is determined by the altitude of the satellite.
Reason for minimum two-stage rocket using for launching of a satellite :
- A rocket is a reaction engine that propels itself forward using the exhaust gases that escape from its back.
- A single-stage rocket launch vehicle would only provide a vertically upward thrust to a satellite. The satellite reaches its maximum speed when all of the rocket fuel has been expended. The greater this speed, the greater the maximum height reached by the satellite. Then gravity will pull it down to the ground. However, if the satellite achieves a high enough speed, it 'escapes' Earth's gravity and floats into space. In any case, it would not become an Earth satellite. As a result, a single-stage rocket is useless.
- Using a two-stage rocket, the empty first-stage is detached and the remaining launch vehicle is rotated through 90°. Then, a controlled and lower thrust by the second—stage gives the correct horizontal velocity, called the critical velocity, to the satellite to put it into a stable circular orbit. This velocity is determined by the altitude of the satellite.
- Hence, a minimum two-stage rocket is necessary to launch a satellite into an orbit around the Earth.
Critical orbital velocity : The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbit round the Earth is called the critical velocity or orbital velocity (vc)
Expression for critical speed
Consider a satellite of mass m revolving round the Earth at height h above its surface.

Let M be the mass of the Earth and R be its radius. If the satellite is moving in a circular orbit of radius (R+h) = r, its speed must be the magnitude of critical velocity vc.
The centripetal force necessary for circular motion of satellite is provided by gravitational force exerted by the Earth on the satellite.
∴ Centripetal force = Gravitational force
∴ \(\frac{mv_{c}^{2}}{r}\)=\(\frac{GmM}{r^2}\)
∴ vc2 = \(\frac{GM}{r}\)
∴ vc2 = \(\frac{GM}{R+h}\)
∴ vc = \(\sqrt{\frac{GM}{R+h}}\)
This is the expression for critical velocity for an orbital radius r = R + h.
The expression shows that critical velocity vc ;
- depends on the orbital radius and the mass of the planet but not on the mass of a satellite
- decreases as altitude increases.
Special case :
When the satellite is revolving close to the surface of the Earth, the height is very small as compared to the radius of the Earth. Hence the height can be neglected and radius of the orbit is nearly equal to R (i.e R>>h, R+h ≈ R)
∴ vc = \(\sqrt{\frac{GM}{R}}\) …..(1)
If g is the acceleration due to gravity,
g = GM/R2
∴ GM = gR2 …..(2)
From Eqs. (1) and (2),
vc = \(\sqrt{gR}\)
If we consider the Earth to be a sphere of average density ρ, then
ρ = mass/volume
∴ ρ = \(\frac{M}{\frac{4}{3}πR^3}\)
∴ M = \(\frac{4}{3}πR^3ρ\) …..(3)
Substituting this value of M in Eq. vc = \(\sqrt{\frac{GM}{R}}\)
∴ vc = \(\sqrt{\frac{G(\frac{4}{3}πR^3ρ)}{R}}\)
= \(\sqrt{\frac{4πρGR^2}{3}}\) = \(2R\sqrt{\frac{πρG}{3}}\)
which is the required expression.
Conditions for various possible orbits of satellite depending upon the horizontal speed of projection :
To put a satellite in an orbit around the Earth, it is raised to some altitude beyond the Earth's atmosphere and then projected horizontally with a velocity v. The path of the satellite depends on the value of v relative to the critical orbital velocity vc and the escape velocity ve.
(i) v < vc : If tangential velocity of projection v is less than the critical velocity, the orbit of satellite is an ellipse with point of projection as apogee (farthest from the Earth) and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere, it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
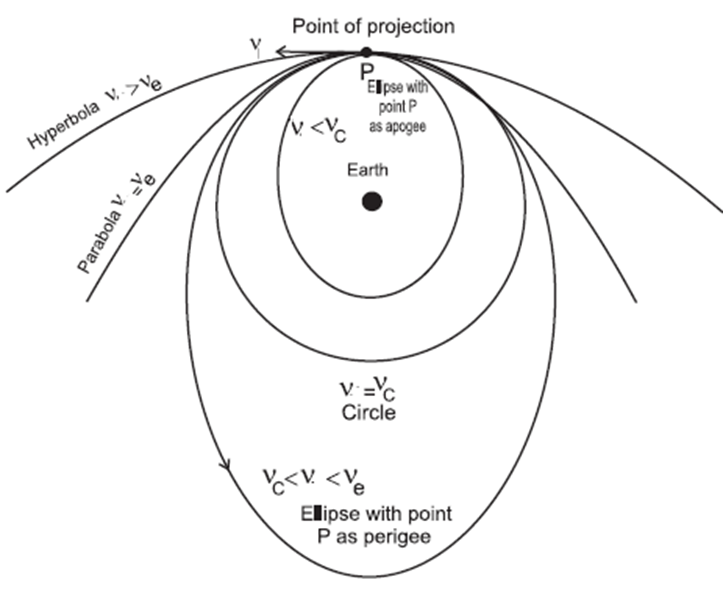
(ii) v = vc : The satellite enters into a circular orbit around the Earth and its motion is a uniform circular motion.
(iii) vc < v < ve : The satellite moves in an elliptical orbit with the centre of the Earth at one focus.
(iv) v > ve : The path of the satellite is no longer a closed curve and it escapes the Earth's gravitational influence.
(v) v = ve : If horizontal speed of projection is equal to the escape speed at that height, the satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
(vi) v > ve : (total energy positive), If horizontal velocity is greater than the escape velocity, the satellite escapes from gravitational influence of Earth transversing a hyperbolic path.
Weightlessness in a Satellite:
According to Newton’s second law of motion, F = ma , where F is the net force acting on an object having acceleration a.
Let us consider the example of a lift or elevator from an inertial frame of reference.
(i) In a lift a person experiences gravitational force in vertically downward direction and normal reaction force in vertically upward direction.
(ii) If a person is standing on a weighing machine in a lift moving with zero acceleration : The lift has zero acceleration. Thus, the magnitude of the net force
F = 0 = N − mg where mg is the gravitational force directed downwards and N is the normal reaction force directed upwards. Thus, the weight of the person recorded by the weighing machine is N = mg.
(iii) If a person is standing on a weighing machine in a lift having net upward acceleration a : The net acceleration in the upward direction means that the upward force N is greater than the downward force mg. Thus, the net force
F = ma = N − mg
∴ N = mg + ma
Thus, the weight of the person recorded by the weighing machine N, is greater than mg.
(iv) If a person is standing on a weighing machine in a lift having net downward acceleration a : The net acceleration in the downward direction means that the downward force mg is greater than the downward force N. Thus, the
F = ma = mg − N
N = mg − ma
Thus, the weight of the person recorded by the weighing machine, N, is less than mg.
(v) If a person is standing on a weighing machine in a lift which is the state of free fall : In this case, the downward acceleration a is equal to the acceleration due to gravity g. Thus, the net force
F = ma = mg − N
N = mg − ma = 0
Thus, the weight of the person recorded by the weighing machine, N, is zero.
Weightlessness experienced by an astronaut in an orbiting satellite :
- The weight of a body is defined as the gravitational force exerted on the body by the Earth. It is directed towards the centre of the Earth.
- When the astronaut is on the surface of the Earth, his weight acts vertically downward. At the same time, the surface of the Earth exerts a force of reaction which is equal in magnitude and opposite in direction to the weight of the astronaut. It is due to this reaction that the astronaut feels his weight.
- When the astronaut is in a spaceship orbiting around the Earth, he feels weightless although the gravitational force acting on the astronaut is not zero.
- The spaceship is an accelerated frame of reference. The spaceship as well as the astronaut are attracted towards the centre of the Earth.
- They have the same centripetal acceleration, equal to the acceleration due to gravity at that height. In this case, a = g, or the satellite (along with the astronaut) is in the state of free fall. Therefore, the astronaut cannot produce any action on the floor of the spaceship. The floor also does not exert a force of reaction on the astronaut. In the absence of the reaction, the astronaut feels weightless.
Q. In spite of free fall, why is the satellite not falling on the earth?
Ans : The revolving satellite is having a tangential velocity which manages to keep it moving in a circular orbit at that height.
Time Period of a Satellite:
Period of revolution of a satellite : The period of revolution of a satellite is the time it takes to complete one revolution around the Earth or any other planet.
The period of revolution of
- the natural satellite of the Earth—the Moon is nearly 27.3 d.
- a geostationary satellite is 1 d, i.e., 24 h.
- a polar satellite is nearly 85 min.
Expression for the period of a satellite in a circular orbit :
Let M and R ≡ mass and radius of the planet (here Earth),
G ≡ gravitational constant,
h ≡ altitude of an orbit,
r = R + h ≡ radius of the circular orbit,
vc ≡ critical orbital speed
T ≡ period of revolution of the satellite.
The critical speed for the circular orbit of radius r is
vc = \(\sqrt{\frac{GM}{r}}\) ….(1)
In one period ( T), the satellite travels a distance equal to the circumference of its circular orbit.
∴ T = circumference/critical speed = 2πr/vc
Substituting for vc from Eq. (1),
T = \(\frac{2πr}{\sqrt{\frac{GM}{r}}}\) = \(2π\sqrt{\frac{r^3}{GM}}\) ...(2)
∴ T = \(2π\sqrt{\frac{(R+h)^3}{GM}}\) ….(3)
This is the required expression for the period of revolution of a satellite.
Squaring both sides of Eq. (2), we get,
T2 = \((\frac{4π^2}{GM})r^3\)
Since the bracketed term is a constant for a given planet,
T2 ∝ r3 …..(4)
Thus, the square of the period of revolution of a satellite is proportional to the cube of the orbital radius.
From the Eq. (3) shows that the period of revolution
- depends on the orbital radius of the satellite and the mass of the planet, but not on the mass of the satellite
- increases as altitude increases.
Period of the satellite in terms of acceleration due to gravity :
The period of revolution of a satellite
T = \(2π\sqrt{\frac{(R+h)^3}{GM}}\) …..(1)
where R = radius of the Earth,
h = altitude of an orbit,
G = universal gravitational constant,
M = mass of the Earth.
Let gh be the acceleration due to gravity at altitude h.
gh = \(\frac{GM}{(R+h)^2}\)
∴ GM = gh(R+h)2 ……(2)
From Eqs. (1) and (2),
T = \(2π\sqrt{\frac{(R+h)^3}{g_h(R+h)^2}}\) = \(2π\sqrt{\frac{(R+h)}{g_h}}\)
Let r = R + h = radius of the circular orbit.
T = \(2π\sqrt{\frac{r}{g_h}}\)
This is the required expression for the period of revolution of a satellite in terms of acceleration due to gravity.
Special case :
When satellite revolves close to the surface of the Earth :
The period of revolution of a satellite in terms of the acceleration due to gravity, in the usual notations,
T = \(2π\sqrt{\frac{(R+h)}{g_h}}\)
When satellite revolves close to the surface of the Earth, R + h ≈ R and gh ≈ g. Hence the minimum period of revolution is
T = \(2π\sqrt{\frac{R}{g}}\) [Such an orbit is called a low-altitude orbit or a Low Earth Orbit (LEO)]
Formula for period of the satellite in terms of density ρ and radius R of planet, when an artificial satellite revolves around a planet in circular orbit close to its surface :
Consider a satellite in a circular orbit of radius r = R + h around a planet, where R is the radius of the planet and h the altitude of the orbit. Let M and ρ be the mass and mean density of the planet. If G is the gravitational constant, the period of revolution of the satellite is
T = \(2π\sqrt{\frac{r^3}{GM}}\) ∴ T2 = \(\frac{4π^2r^3}{GM}\) ...(1)
For a low altitude orbit, h<< R, so that r = R + h ≈ R and
T2 ≈ \(\frac{4π^2R^3}{GM}\) …..(2)
Now, mean density of the planet, ρ = mass/volume
∴ ρ = \(\frac{M}{\frac{4}{3}πR^3}\)
∴ M = \(\frac{4}{3}πR^3ρ\) …….(3)
Substituting this value of M in Eq. (2), we get,
T2 = \(\frac{4π^2r^3}{G(\frac{4}{3}πR^3ρ)}\) =\(\frac{3π}{ρG}\)
∴ T = \(\sqrt{\frac{3π}{ρG}}\) …(4)
which is the required expression.
Binding Energy of an orbiting satellite:
Binding Energy of body :
- Every body in the gravitational field of the Earth is bound to the Earth by the gravitational force of attraction.
- In order to separate this bound system, the body must be given sufficient energy so that it can become free of the Earth's gravity and escape to infinity. The minimum energy required for this is called the binding energy of the body.
Expression for Binding Energy of body rest on the Earth’s surface :
Consider a body of mass m at rest on the Earth's surface, so that its kinetic energy (KE) is zero.
Let M and R be the mass and radius of the Earth and G the gravitational constant.
The gravitational potential at a point on the Earth’s surface = −GM/R
Then, the gravitational potential energy (PE) of the body = \(-\frac{GM}{R}×m\) = \(-\frac{GMm}{R}\)
Total energy of the body, E = PE + KE
∴ E = \(-\frac{GMm}{R}\) + 0 = \(-\frac{GMm}{R}\)
The minus sign in the above expression shows that the body is bound to the Earth.
If we provide the energy \(\frac{GMm}{R}\) to the body, its total energy will become zero, i.e., it will become just free from the gravitational influence of the Earth.
Therefore, the binding energy of the body,
BE = − E = \(\frac{GMm}{R}\)
Binding energy of a satellite : It is defined as the minimum energy that should be provided to the satellite to make it free from the gravitational influence of the Earth.
Expression for binding energy of a satellite revolving around the Earth at a certain altitude :
Consider a satellite performing uniform circular motion around the Earth.
Let m = mass of the satellite,
M = mass of the Earth,
R = radius of the Earth,
h = height of the satellite from the surface of the Earth,
r ( = R + h) = radius of the orbit of the satellite,
vc = critical orbital speed of the satellite.
G = gravitational constant.
The gravitational potential at a point at a distance r from the centre of the Earth
= \(-\frac{GM}{r}\) [for r ≥ R ] ...(1)
Gravitational potential energy (PE) of the satellite = \(-\frac{GM}{r}×m\) = \(-\frac{GMm}{r}\) ...(2)
Kinetic energy (KE) of the satellite = \(\frac{1}{2}\)mvc2
And vc2 = GM/r
∴ KE = \(\frac{1}{2}\)m x \(\frac{GM}{r}\) = \(\frac{GMm}{2r}\)
Total energy of the satellite, E = PE + KE
∴ E = \(-\frac{GMm}{r}\) + \(\frac{GMm}{2r}\) = \(-\frac{GMm}{2r}\) = \(-\frac{GMm}{2(R+h)}\)
The minus sign in the expression for the total energy shows that the satellite is bound to the Earth.
If we provide the energy \(\frac{GMm}{2r}\) to the satellite, its total energy will become zero, and hence, it will become free from the gravitational influence of the Earth.
∴ Binding energy of the satellite = −E = \(\frac{GMm}{2r}\) = \(\frac{GMm}{2(R+h)}\)
It shows that the binding energy of a satellite depends
- directly on the mass of the satellite
- directly on the mass of the Earth
- inversely on its distance r = R + h from the centre of the Earth.
Escape velocity of a satellite : The escape velocity of a satellite is the minimum velocity with which it should be projected vertically upwards from the surface of the Earth so that it escapes from the Earth's gravitational field.
Expression for Escape speed of a satellite :
Suppose a satellite of mass m is in a circular orbit of radius r = R + h around the Earth, where R is the radius of the Earth and h the altitude of the orbit. The critical orbital speed for the orbit is
vc = \(\sqrt{\frac{GM}{r)}}\) …..(1)
where M is the mass of the Earth and G the gravitational constant.
The satellite has a potential energy
PE = \(\frac{GMm}{r}\) …..(2)
It just escapes the gravitational influence of the Earth when its total energy E is zero. If ve is its escape speed from the orbit, then it must have a kinetic energy mve2 such that
E = \(\frac{1}{2}\)mve2 + PE = 0
∴ \(\frac{1}{2}\)mve2 = −PE = \(\frac{GMm}{r}\)
∴ ve = \(\sqrt{\frac{2GM}{r)}}\) ….(3)
This is the required equation.
Dividing Eq. (3) by Eq. (1), we get,
ve = \(\sqrt{2}\)vc ……(4)
Therefore, the escape speed of a satellite from its orbit is times its critical orbital speed.
Since, the satellite already has a speed vc, Eq. (4) shows that it requires an additional speed of 0.414 vc to escape from its orbit and the gravitational influence of the Earth.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 4: Laws of Motion – Online Notes
Next Chapter : Chapter 6: Mechanical Properties of Solids – Online Notes
We reply to valid query.