Solid State
Maharashtra Board-Class-12-Chemistry-Chapter-1
Solution
Question 1.
Choose the most correct answer.
i. Molecular solids are
a. crystalline solids
b. amorphous solids
c. ionic solids
d. metallic solids
a. amorphous solids
ii. Which of the following is n-type semiconductor?
a. Pure Si
b. Si doped with As
c. Si doped with Ga
d. Ge doped with In
b. Si doped with As
iii. In Frenkel defect
a. electrical neutrality of the substance is changed.
b. density of the substance is changed.
c. both cation and anion are missing
d. overall electical neutrality is preserved.
d. overall electical neutrality is preserved.
iv. In crystal lattice formed by bcc unit cell the void volume is
a. 68 %
b. 74 %
c.32 %
d. 26 %
c.32 %
v. The coordination number of atoms in bcc crystal lattice is
a. 2
b. 4
c. 6
d. 8
d. 8
vi. Which of the following is not correct?
a. Four spheres are involved in the formation of tetrahedral void.
b. The centres of spheres in octahedral voids are at the apices of a regular tetrahedron.
c. If the number of atoms is N the number of octahedral voids is 2N.
d. If the number of atoms is N/2, the number of tetrahedral voids is N.
c. If the number of atoms is N the number of octahedral voids is 2N.
vii. A compound forms hcp structure. Number of octahedral and tetrahedral voids in 0.5 mole of substance is respectively
a. 3.011×1023, 6.022×1023
b. 6.022×1023, 3.011×1023
c. 4.011×1023, 2.011×1023
d. 6.011×1023, 12.022×1023
a. 3.011×1023, 6.022×1023
viii. Pb has fcc structure with edge length of unit cell 495 pm. Radius of Pb atom is
a. 205 pm
b. 185 pm
c. 260 pm
d. 175 pm
d. 175 pm
Question 2.
Answer the following in one or two sentences
i. What are the types of particles in each of the four main classes of crystalline solids ?
In each of the four main classes of crystalline solids, the smallest constituents or particles of various solids are atoms, ions or molecules.
ii. Which of the three types of packing used by metals makes the most efficient use of space and which makes the least efficient use?
fcc has the most efficient packing of particles while scc has the least efficient packing.
iii. The following pictures show population of bands for materials having different electrical properties. Classify them as insulator, semiconductor or a metal.

Picture A represents metal conductor, Picture B represents insulator, Picture C represents semiconductor.
iv. What is the unit cell?
Unit cell : It is the smallest repeating structural unit of a crystalline solid (or crystal lattice) which when repeated in different directions produces the crystalline solid (lattice).
v. How does electrical conductivity of a semiconductor change with temperature? Why?
vi. The picture represents bands of MOs for Si. Label valence band, conduction band and band gap.

vii. A solid is hard, brittle and electrically nonconductor. Its melt conducts electricity. What type of solid is it?
A solid crystalline electrolyte like NaCl is having above properties. NaCl is hard, brittle and electrically nonconductor. But its melt conducts electricity.
viii. Mention two properties that are common to both hcp and ccp lattices.
In hcp and ccp ciystal lattices coordination number is 12 and packing efficiency is 74%.
ix. Sketch a tetrahedral void.

x. What are ferromagnetic substances?
Question 3.
Answer the following in brief.
i. What are valence band and conduction band?
ii. Distinguish between ionic solids and molecular solids.

iii. Calculate the number of atoms in fcc unit cell.
Number of atoms in face-centred cubic (fcc) unit cell : In this unit cell, there are 8 atoms at 8 corners and 6 atoms at 6 face centres. Each comer contributes 1/8th atom to the unit cell, hence due to 8 corners, ∴ Number of atoms present in the unit cell = (1/8) X 8 = 1 Each face centre contributes half of the atom to the unit cell, hence due to 6 face centres, Number of atoms =1/2 x 6 = 3. Total number of atoms present in fcc unit cell = 1 + 3 = 4. Hence the volume of the unit cell is equal to the volume of four atoms.

iv. How are the spheres arranged in first layer of simple cubic close-packed structures? How are the successive layers of spheres placed above this layer?
Three dimensional crystal structures are obtained by stacking of two dimensional layers. Simple cubic lattice is obtained by stacking of two dimensional square layers. The stacking of two dimensional hexagonal close packed layers gives two structures namely hexagonal close packed (hcp) structure and face centred (fcc) structure. (i) Stacking of square close packed layers : In this arrangement, the two dimensional AAAA type square closed packed layers are placed one over the other in such a way that the crests of all spheres are in contact with successive layers in all directions. All spheres of different layers are perfectly aligned horizontally and vertically forming unit cells having primitive or simple cubic structure. Since all the layers are identical and if each layer is labelled as layer A, then whole three dimensional crystal lattice will be of type. Each sphere is in contact with six surrounded spheres, hence the co-ordination number of each sphere is six. (ii) Stacking of two hexagonal close packed layers : A close packed three dimensional structure can be generated by arranging hexagonal close packed layers in a particular manner. In this the spheres of second layer are placed in the depression of the first layer. In this if first layer is labelled as A then second layer is labelled as B since they are aligned differently. In this, all triangular voids of the first layers are not covered by the spheres of the second layer. The triangular voids which are covered by second layer spheres generate tetrahedral void which is surrounded by four spheres. The triangular voids in one layer have above them triangular voids of successive layers. The overlapping triangular voids from two layers together form an octahedral void which is surrounded by six spheres.


v. Calculate the packing efficiency of metal crystal that has simple cubic structure.
Packing efficiency of metal crystal in simple cubic lattice : Step 1 : Radius of sphere : In simple cubic unit cell, particles (spheres) are at the corners and touch each other along the edge. A face of simple cubic unit cell is shown in Fig. It is evident that a = 2r or r = a/2 ………(1) where r is the radius of atom and ‘a’ is the length of unit cell edge. Step 2 : Volume of sphere : Volume of a sphere = .\(\frac{4π}{3}×r^3\) Substitution for r from Eq. (1) ∴ Volume of one particle = \(\frac{4π}{3}(\frac{a}{2})^3\) = \(\frac{πa^3}{6}\) Step 3 : Total volume of particles : Because simple cubic unit cell contains only one particle, volume occupied by particle in unit cell = \(\frac{πa^3}{6}\) Step 4 : Packing efficiency Packing efficiency = \(\frac{\text{Volume occupied by particles in unit cell}}{\text{total volume of unit cell}}×100\) = \(\frac{πa^3/6}{a^3}×100 = \frac{π}{6}×100=\frac{3.142}{6}×100 \) = 52.36% Thus, in simple cubic lattice, 52.36 % of total space is occupied by particles and 100−52.36 = 47.64 % is empty space, ∴ void volume or a percentage of void space=.47.64 %

vi. What are paramagnetic substances? Give examples.
Paramagnetic substances : The magnetic properties of a substance arise due to the presence of electrons. An electron while revolving around the nucleus, also spins around its own axis and generates a magnetic moment and magnetic properties.
vii. What are the consequences of Schottky defect?
Consequences of Schottky defect :
viii. Cesium chloride crystallizes in cubic unit cell with Cl- ions at the corners and a Cs+ ion in the centre of the cube. How many CsCl molecules are there in the unit cell?
Number of Cs+ ion at body centre = 1 A Number of Cl- ions due to 8 comers = \(\frac{1}{8}×8\) = 1 Hence unit cell contains 1 CsCl molecule.
ix. Cu crystallizes in fcc unit cell with edge length of 495 pm. What is the radius of Cu atom?
Given : a = 495 pm Radius, r = ? For fcc structure, Radius = r = \(\frac{a}{2\sqrt{2}}= \frac{495}{2\sqrt{2}}\) = 175pm Ans. Radius of Cu atom = 175 pm.
x. Obtain the relationship between density of a substance and the edge length of unit cell.
Consider edge length of cubic unit cell is a, the ∴ Volume of unit cell = a3. Suppose that mass of one particle is m and that there are n particles per unit cell. ∴ Mass of unit cell = m × n The density of unit cell (ρ), which is same as density of the sub-substance is given by Density of Unit Cell = \(\frac{\text{mass of unit cell}}{\text{volume of unit cell}}\) ∴ ρ = \(\frac{m×n}{a^3}\)
Question 4.
The density of iridium is 22.4 g/cm3. The unit cell of iridium is fcc. Calculate the radius of iridium atom. Molar mass of iridium is 192.2 g/mol.
Given : Crystal structure of iridium = fcc Molar mass of iridium = 192.2 gmol-1 Density = ρ = 22.4 gcm-3 Radius of iridium = ? In fcc structure, there are 8 Ir atoms at 8 corners and 6 Ir atoms at 6 face centres. Total number of Ir atoms = \(\frac{1}{8}×8 +\frac{1}{2}×6 \) = 1+3 = 4 Mass of Ir atom = = 31.92 x 10-23 g ∴ Mass of 4 Ir atoms = 4 x 31.92 x 10-23 g = 1.277 x 10-21 g Mass of unit cell = 1.277 x 10-21 g Density of unit cell = \(\frac{\text{mass of unit cell}}{\text{volume of unit cell}}\) 22.4 = \(\frac{1.277×10^{-21}}{a^3}\) a3 = \(\frac{1.277×10^{-21}}{22.4}\) = 57 x 10-24 cm3 ∴ a = \((57×10^{-24})^{\frac{1}{3}}\) = 3.848 x 10-8 cm If r is the radius of iridium atom, then for fcc structure, r = \(\frac{a}{2\sqrt{2}}=\frac{3.848×10^{-8}}{2\sqrt{2}}\) = 1.36 x 10-8 cm = 136 pm Ans: Radius of iridium atom = 136 pm.
Question 5.
Aluminium crystallizes in cubic close packed structure with unit cell edge length of 353.6 pm. What is the radius of Al atom? How many unit cells are there in 1.00 cm3 of Al?
Given : Structure of Al = Cubic close packed structure = ccp structure Edge length of unit cell = a = 353.6 pm = 3.536 x 10-8 cm r = ? Number of unit cells in 1.00 cm3 of Al = ? (...V= 1.00 cm3 ) Radius of Al atom = r = \(\frac{a}{2\sqrt{2}}=\frac{353.6}{2\sqrt{2}}\) = 125 pm Ans. Radius of Al atom = 125 pm Volume of one unit cell = a3 = (3.536 x 10-8)3 = 4.421 x 10-23 cm3 Number of unit cells = \(\frac{V}{a^3}=\frac{1.00}{4.421×10^{-23}}\) = 2.26 X 1022 Ans. Number of unit cells = 2.26 x 1022.
Question 6.
In an ionic crystalline solid atoms of element Y form hcp lattice. The atoms of element X occupy one third of tetrahedral voids. What is the formula of the compound ?
In the given hcp lattice, Y atoms are present at 12 corners and 2 face centres. ∴ Number of Y atoms = \(\frac{1}{6}×12 +\frac{1}{2}×2 \) = 2+1= 3 There are 6 tetrahedral voids, the number of X atoms = \(\frac{1}{3}×6\) = 2 ∴ Formula of the compound is X2Y3.
Question 7.
How are tetrahedral and octahedral voids formed?
Tetrahedral void: All triangular voids of the first layers are not covered by the spheres of the second layer. The triangular voids that are covered by spheres of the second layer generate tetrahedral void. The vacant space or void among four constituent particles having tetrahedral arrangement in the crystal lattice is called tetrahedral void. The arrangement of four spheres around the void is tetrahedral. A tetrahedral void is formed when a triangular void made by three coplanar spheres is in contact with fourth sphere above or below it. Octahedral void : The overlapping triangular voids from the two layers together form an octahedral void which is surrounded by six spheres. The vacant space or void at the centre of six spheres (or atoms) which are placed octahedrally is called octahedral void. 

Question 8.
Third layer of spheres is added to second layer so as to form hcp or ccp structure.
What is the difference between the addition of third layer to form these hexagonal close-packed structures?
In the formation of hexagonal closed-packed (hcp) structure, the first one dimensional row shows depressions between neighbouring atoms. When a second row is arranged so that spheres fit in these depressions then a staggered arrangement is obtained. If the first row is A then the second row is B. When third row is placed in staggered manner in contact with second row then A type arrangement is obtained. Similarly, the spheres in fourth row can be arranged as B type layer. This results in ABAB type setting of the layers. This gives hexagonal close packing (hcp) structure.

Question 9.
An element with molar mass 27 g/mol forms cubic unit cell with edge length of 405 pm. If density of the element is 2.7 g/cm3. What is the nature of cubic unit cell?
Given : Molar mass = M= 27 g m0l_‘ Nature of crystal = cubic unit cell Edge length = a = 405 pm = 4.05 x 10-8 cm Density = ρ = 2.7 g cm-3 Nature of unit cell = ? ρ = \(\frac{m×n}{a^3×N_A}\) ∴ n = \(\frac{ρa^3×N_A}{m}\) = \(\frac{2.7(4.05×10^{-8})^3×6.022x10^{23}}{27}\) = 3.997 ≅ 4 Hence the nature of unit cell is face-centred cubic, unit cell Ans. The nature of cubic unit cell is fcc.
Question 10.
An element has a bcc structure with unit cell edge length of 288 pm. How many unit cells and number of atoms are present in 200 g of the element?
(Density of element 7.2 gm/cm3 )
Given: Types of unit cell = bcc, for bcc unit cell n = 2 Edge length (a) = 288 pm = 2.88 x 10-8 cm3 Mass of element (x) =200g Density of element (r) = 7.2 gm/cm3 Number of unit cell in x g of element = \(\frac{x}{ρa^3}\) = \(\frac{200}{7.2×(2.88×10^{-8})^3}\) = 1.16 x 1024 Number of atoms in x g of element = \(\frac{nx}{ρa^3}\) = \(\frac{2x}{ρa^3}\)= 2 × 1.16 x 1024 = 2.32 x 1024 Ans. Number of unit cell in x g of element = 1.16 x 1024 Number of atoms in x g of element = 2.32 x 1024
Question 11.
Distinguish with the help of diagrams metal conductors, insulators and semiconductors from each other.
Conductor : 1) A substance which conducts heat and electricity to a greater extent is called conductor. 2) In this, conduction bands and valence bands overlap or are very closely spaced. 3) There is no energy difference or very less energy difference between valence bands and conduction bands. 4) There are free electrons in the conduction bands. 5) The conductance decreases with the increase in temperature. 6) The conducting properties can’t be improved by adding third substance. 7) E.g., Metals, alloys. Insulator : 1) A substance which cannot conduct heat and electricity under any conditions is called insulator. 2) In this, conduction bands and valence bands are far apart. 3) The energy difference between conduction bands and valence bands is very large. 4) There are no free electrons in the conduction bands and electrons can’t be excited from valence bands to conduction bands due to large energy difference. 5) No effect of temperature on conducting properties. 6) No effect of addition of any substance. 7) E.g., Wood, mbber, plastics. Semiconductor: 1) A substance which has poor electrical conductance at low temperature but higher conductance at higher temperature is called semiconductor. 2) In this, conduction bands and valence bands are spaced closely. 3) The energy difference between conduction bands and valence bands is small. 4) The electrons can be easily excited from valence bands to conduction bands by heating. 5) Conductance increases with the increase in temperature. 6) By doping, conducting properties improve. E.g. n-type, p-type semiconductors. 7) E.g., Si, Ge.



Question 12.
What are n-type semiconductors? Why is the conductivity of doped n-type semiconductor higher than that of pure semiconductor? Explain with diagram.
n-type semiconductor :
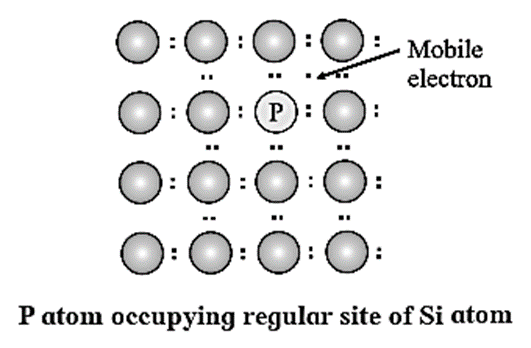
Question 13.
Explain with diagram, Frenkel defect. What are the conditions for its formation? What is its effect on density and electrical neutrality of the crystal?
Frenkel defect : This defect arises when an ion of an ionic compound is missing from its regular site and occupies interstitial vacant position between lattice points. Conditions for the formation of Frenkel defect : Consequences of Frenkel defect : 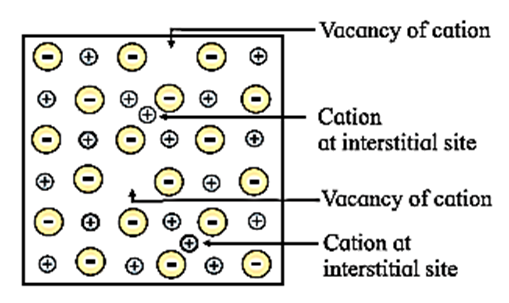
Question 14.
What is an impurity defect? What are its types? Explain the formation of vacancies through aliovalent impurity with example.
Impurity defect : This defect arises when foreign atoms, that is, atoms different from the host atoms are present in the crystal lattice. There are two types of impurity defects namely (1) Substitutional defects and (2) Interstitial defects. i. Substitutional impurity defect : In this defect, the foreign atoms are found at the lattice sites in place of host atoms. The regular atoms are displaced from their lattice sites by impurity atoms. For example : Solid solutions of metals (alloys) : Brass is an alloy of Cu and Zn. In brass, host Cu atoms are replaced by impurity of Zn atoms. The Zn atoms occupy regular sites of Cu atoms as shown in Fig. ii. Interstitial impurity defect : A defect in solid in which the impurity atoms occupy interstitial vacant spaces of lattice structure is called interstitial impurity defect. For example, in steel, normal lattice sites are occupied by Fe atoms but interstitial spaces are occupied by carbon atoms. . Vacancy through aliovalent impurity : (By addition of impurities of aliovalent ions) When aliovalent ion like Sr2+ in small amount is added by adding SrCl2 to NaCl during its crystallisation, each Sr2+ ion (oxidation state 2 +) removes 2 Na+ ions from their lattice points, to maintain electrical neutrality. Hence one of vacant lattice site is occupied by Sr2+ ion while other site remains vacant.



PDF : Class-12-Chemistry-Chapter-1-Solid State-Text Book
PDF : Class-12-Chemistry-Chapter-1-Solid State- Notes
PDF : Class-12-Chemistry-Chapter-1-Solid State- Solution
All 16 Chapters Notes -Class-12-Chemistry (16-PDF)
All 16 Chapters Solutions -Class-12-Chemistry (16-PDF)
All 16 Chapters Notes+Solutions -Class-12-Chemistry (32-PDF)
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Solutions – Online Notes
We reply to valid query.