States of Matter
Maharashtra State Board-Class-11-Science-Chemistry-Chapter -10
Solutions
Question 1. Select and write the most appropriate alternatives from the given choices.
(A) The unit of viscosity is
(a) dynes
(b) newton
(c) gram
(d) poise
(d) poise
(B) Which of the following is true for 2 moles of an ideal gas ?
(a) PV = nRT
(b) PV = RT
(c) PV = 2RT
(d) PV = T
(c) PV = 2RT
(C) Intermolecular forces in liquid are -
(a) greater than gases
(b) less than solids
(c) both (a) and (b)
(d) greater than solids
(c) both (a) and (b)
(D) Interactive forces are .......... in ideal gas.
(a) nil
(b) small
(c) large
(d) same as that of real gases
(a) nil
(E) At constant temperature the pressure of 22.4 dm3 volume of an ideal gas was increased from 105 kPa to 210 kPa, New volume could be
(a) 44.8 dm3
(b) 11.2 dm3
(c) 22.4 dm3
(d) 5.6 dm3
(b) 11.2 dm3
Question 2. Answer in one sentence.
(A) Name the term used for mixing of different gases by random molecular motion and frequent collision.
Different gases can be mixed by diffusion.
(B) The pressure that each individual gas would exert if it were alone in the container, what do we call it as ?
The pressure that each individual gas would exert if it were alone in the container containing gaseous mixture is called partial pressure.
(C) When a gas is heated the particles move more quickly. What is the change in volume of a heated gas if the pressure is kept constant ?
When the gas heated at constant pressure the volume of the gas increases.
(D) A bubble of methane gas rises from the bottom of the North sea. What will happen to the size of the bubble as it rises to the surface ?
As a bubble of methane gas rises from the bottom of the sea, the pressure above the
bubble due to water level decreases hence the size of the bubble increases.
(E) Convert the following temperatures from degree celcius to kelvin.
(a) -15° C
(b) 25° C
(c) -197° C
(d) 273° C
(a) T = 273 - 15 = 258 K
(b) T = 273 + 25 = 298 K
(c) T = 273 - 197 = 76 K
(d) T = 273 + 273 = 546 K.
(F) Convert the following pressure values into Pascals.
(a) 10 atmosphere
(b) 1 kPa.
(c) 107000 Nm-2
(d) 1 atmosphere
(a) Pressure = 10 x 101325 Pa = 1013250 Pa
(b) Pressure = 1 kPa = 1 x 103 Pa
(c) Pressure = 107000 Nm-2 = 107000 Pa
(d) Pressure = 1 atmosphere = 101325 Pa.
(G) Convert :
(a) Exactly 1.5 atm to pascals
(b) 89 kPa to newton per square metre (Nm-2)
(c) 101.325 kPa to bar
(d) -100 °C to kelvin
(e) 0.124 torr to standard atmosphere
(a) Pressure = 1.5 x 101325 Pa = 151987.5 Pa
(b) Pressure = 89 kPa = 89 x 103 Pa = 89 x 103 Nm-2
(c) Pressure = 101.325 kPa = 101.325 x 103 Pa
= \(\frac{101.325×10^3}{1×10^5}\) bar
= 101.325 × 10-2 bar
= 1.01325 bar
(d) Temperature = 273 + (-100) = 173 K
(e) Pressure = 0.124 torr = \(\frac{0.124}{760}\) atm = 1.631 x 10-4 atm.
(H) If density of a gas is measured at constant temperature and pressure then which of the following statement is correct ?
(a) Density is directly proportional to molar mass of the gas.
(b) Greater the density greater is the molar mass of the gas.
(c) If density, temperature and pressure is given ideal gas equation can be used to find molar mass.
(d) All the above statements are correct.
(a) Correct (b) Correct (c) Correct. (d) Correct.
(I) Observe the following conversions.

Which of the above reactions is in accordance with the principle of stoichiometry ?
The reaction represented in (a) is in accordance with the principle of stoichiometry.
(J) Hot air balloons float in air because of the low density of the air inside the balloon. Explain this with the help of an appropriate gas law.
The air inside the balloons has low density due to low pressure and high volume. Hence the air balloons float in air. This can be explained by Boyle's law.
Question 3. Answer the following questions.
(A) Identify the gas laws from the following diagrams.

(a) Boyle's law
(b) Charles law
(c) Avogadro law.
(B) Consider a sample of a gas in a cylinder with a movable piston.

Show digramatically the changes in the position of piston, if -
(a) Pressure is increased from 1.0 bar to 2.0 bar at constant temperature.
(b) Temperature is decreased from 300 K to 150 K at constant pressure
(c) Temperature is decreased from 400 K to 300 K and pressure is decreased from 4 bar to 3 bar.
(a) At constant temperature since the pressure is doubled, the volume will become half.

(b) At constant pressure temperature is decreased 1 times i.e. 300 K to 150 K. Hence, the volume of the gas will become half, as shown in (a).
(c) Let the initial volume of the gas be V.
P1 = 4 bar, P2 = 3 bar, T1 = 400 K, T2 = 300 K
If V' is the final volume then,
\(\frac{P_1V}{T_1}=\frac{P_2V'}{T_2}\)
∴ \(\frac{V'}{V}=\frac{P_1×T_2}{P_2×T_1}\) = \(\frac{V'}{V}=\frac{4×300}{3×400}\) = 1
∴ V’ = V
Since the volume of the gas remains the same the piston will remain at the same position.
(D) List the characteristic physical properties of the gases.
The gaseous state is characterized by the following physical properties :
- Gases are lighter than solids and liquids, resulting in lower density.
- Gases occupies entire space and takes container shape.
- Gas molecules are widely separated and in continuous motion, exerting equal pressure.
- Intermolecular forces are weakest in gases.
- Gases possesses diffusion property, a spontaneous homogenous intermixing of gases.
- Gases are highly compressible.
(E) Define the terms:
(a) Polarizability
The distortion in the electron cloud caused by the attractive and repulsive interactions between the nuclei of two approaching non-polar molecules is known as polarizability.
- More electrons in a molecule increase polarisability.
- Defines how external electric field can alter an atom's or molecule's electron cloud.
(b) Hydrogen bond
A hydrogen bond is a special type of dipole-dipole attraction which occurs when a hydrogen atom is bonded to a strongly electronegative atom or an atom with a lone pair of electrons.
(c) Aqueous tension
Aqueous tension : In case of pure water or an aqueous solution, there exists saturated water vapour in equilibrium with it on its surface and the pressure of this vapour is called aqueous tension.
(d) Dipole moment
Dipole moment (μ) of al polar molecule is the product of the magnitude of the charge (Q) and the distance (r) between the centres of positive and negative charges. It is designated by a Greek Letter (u) and its unit is Debye (D).

It is represented as, μ = Q × r
- Dipole moment is a vector quantity and represented by a small arrow with tail at the positive centre and head towards the negative centre.
- The polar molecules have permanent dipole moment.
(F) Would it be easier to drink water with a straw on the top of the Mount Everest or at the base ? Explain.
Atmospheric pressure is crucial for the process of drinking water through a straw. It reduces the pressure inside the straw, allowing the liquid to be pushed up to the mouth. However, the pressure difference on the top of Mount Everest is very low, making it difficult to drink water with a straw compared to the base.
(G) Identify type of the intermolecular forces in the following compounds.
(a) CH3 - OH
(b) CH2 - CH2
(c) CHCl3
(d) CH2Cl2
(a) Hydrogen bonding
(b) London dispersion forces
(c) Dipole-dipole interactions
(d) Dipole-dipole interactions.
(H) Name the types of intermolecular forces present in Ar, Cl2, CCl4 and HNO3
(a) London dispersion forces
(b) London dispersion forces
(c) Dipole-dipole interactions
(d) Hydrogen bonding.
(I) Match the pairs of the following :
| ‘A’ | ‘B’ |
| a. Boyle’s law | i. at constant pressure and volume |
| b. Charles’ law | ii. at constant temperature |
| iii. at constant pressure |
(a) Boyle's law-at constant temperature
(b) Charles' law-at constant pressure.
(J) Write the statement for :
(a) Boyle’s law (b) Charles’ law
(a) Boyle’s law : For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of a gas is inversely proportional to the volume (V) of gas.
(b) Charles’ law : It states that at constant pressure, the volume of the given mass of a gas is directly proportional to its absolute temperature.
- It states that at constant pressure the volume of a given mass of a gas increases or decreases by \(\frac{1}{273.15}\) of its volume at 0 °C for every degree rise or fall of temperature.
(K) Differentiate between Real gas and Ideal gas.
| Real gas | Ideal gas |
| A gas which does not obey gas laws or an ideal gas equation is called a real gas.
Practically almost all gases are real gases but they tend towards an ideal behaviour at low pressure and high temperature. |
A gas that follows strictly all the three laws; Boyle's law, Charles' law and Avogadro law and ideal gas equation (PV = nRT) is an ideal gas.
|
| Molecules are not perfectly elastic. | Molecules are perfectly elastic. |
| Intermolecular attraction is present, hence, collision takes place with loss of kinetic energy. | No attraction or repulsion between the gas molecules i.e. collision without loss of kinetic energy (K.E.) |
| Actual volume of individual gas molecule is significant at high pressure and low temperature. | Actual volume of the gas molecules is negligible as compared to total volume of the gas. |
| Undergoes liquefaction at low temperature when cooled and compressed. | It doesn't liquify even at low temperature but continues to obey Charles’ law and finally occupies zero volume at — 273 °C. |
| Gases that exist in nature like H2, O2, CO2, N2, He, etc. | Such a gas does not exist. |
Question 4. Answer the following questions
(A) State and write mathematical expression for Dalton’s law of partial pressure and explain it with suitable example.
Statement : The total pressure of a mixture of two or more unreactive gases is the sum of the partial pressures of the individual gases in the mixture.
Example : If P1, P2, P3, .... .. are partial pressures of constituent gases in the mixture at constant volume and temperature then by Dalton’s law, total pressure is,
PTotal = P1 + P2 + P3 + .... ..
This is mathematical statement of Dalton’s law.
(B) Derive an Ideal gas equation. Mention the terms involved in it. Also write how it is utilised to obtain combined gas law.
Derivation of Ideal Gas Equation :
The three gas laws, namely, Boyle’s law, Charles law and Avogadro law, are combined mathematically to obtained what is called ideal gas equation.
Consider n moles of a gas occupying volume V at pressure P and temperature T.
(i) By Boyle's law, at constant temperature,
V ∝ 1/P (at constant n and T)
(ii) By Charles’ law, at constant pressure,
V ∝ T (at constant n and P)
(iii) By Avogadrds law, at constant pressure and temperature,
V ∝ n (at constant P and T)
Hence,
V ∝ \(\frac{n×T}{P}\)
∴ V = \(\frac{nRT}{P}\) OR PV = nRT
where R is a proportionality constant and called gas constant or universal gas constant.
The equation, PV = nRT is called an ideal gas equation or an equation of state.
- If m is the mass of the gas then, number of moles, n = m/M Hence, ideal gas equation can be written as, PV = \(\frac{mRT}{M}\).
Combined Gas law :
Consider n moles of a gas. By ideal gas equation,
PV = nRT
\(\frac{PV}{T}\) = nR = constant. (Since n and R are constant)
Hence, for a given gas,
\(\frac{P_1V_1}{T_1}\) = \(\frac{P_2V_2}{T_2}\)
This equation is also called Combined gas law or combined gas equation.
(C) With the help of graph answer the following –

At constant temperature,
(a) Graph shows relation between pressure and volume. Represent the relation mathematically.
(b) Identify the law.
(c) Write the statement of law.
(a) P ∝ \(\frac{1}{V}\)
(b) Boyle's law
(c) Statement : For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of a gas is inversely proportional to the volume (V) of gas.
(D) Write Postulates of kinetic theory of gases.
- Gases consist of tiny particles (molecules or atoms).
- On average, gas molecules remain far apart from each other. Therefore, the actual volume of the gas molecules is negligible as compared to the volume of the container. Hence, gases are highly compressible.
- The attractive forces between the gas molecules are negligible at ordinary temperature and pressure. As a result, the gas expands to occupy the entire volume of the container.
- Gas molecules are in constant random motion and move in all possible directions in straight lines. They collide with each other and with the walls of the container.
- Pressure of the gas is due to the collision of gas molecules with the walls of the container.
- The collisions of the gas molecules are perfectly elastic in nature, which means that the total energy of the gaseous particle remains unchanged after the collision.
- The different gas molecules move with different velocities at any instant and hence have different kinetic energies.
- However, the average kinetic energy of the gas molecules is directly proportional to the absolute temperature.
(E) Write a short note on -
(a) Vapour pressure.
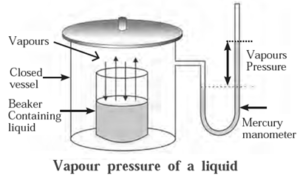
The pressure exerted by the vapour in equilibrium with the liquid is known as saturated vapour pressure or simply vapour pressure.
The vapour pressure of water is also called Aqueous Tension.
Explanation :
- All liquids have a tendency of evaporation, during which liquid molecules escape into a gaseous state (vapour).
- If the vessel is closed then the vapour molecules get accumulated on the liquid surface.
- These molecules due to random motion collide with each other and on the walls of a container and get condensed back into the liquid.
- When an equilibrium is attained between evaporation and condensation the number of vapour molecules remain constant giving a definite vapour pressure at constant temperature.
- Mercury manometer may be used to measure the vapour pressure of a‘ liquid as shown in below Fig.
(b) Surface tension
Surface Tension :
The force acting per unit length perpendicular to the line drawn on the surface of liquid is called surface tension.
- Unit : Surface tension is measured in SI Unit, Nm-1, denoted by Greek letter “γ’’ (Gamma)
Explanation:
- In the bulk of a liquid, every molecule is surrounded equally and symmetrically by other neighbouring molecules of the liquid. Hence, all bulk molecules experience balanced forces.
- But on the surface, the molecules experience downward attractive forces from the molecules in the bulk.
- Since there are no molecules above the liquid surface they experience net force of attraction in the downward direction towards the bulk of the liquid. Therefore, the liquid surface behaves like a ‘stretched membrane which is always under a tension. This gives rise to a surface tension on the liquid surface.

Application of surface tension :
- Cleaning action of soap and detergent is due to the lowering of interfacial tension between water and oily substances. Due to lower surface tension, the soap solution penetrates into the fibre, surrounds the oily substance and washes it away.
- The effective use of toothpastes, mouth washes and nasal drops is due to the presence of substances having lower surface tension. This increases the efficiency of their penetrating action.
(c) Viscosity.
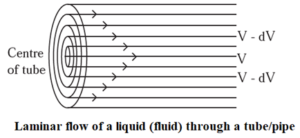
Viscosity is the force of friction between the successive layers of a flowing liquid.
OR It is the resistance to the flow of a liquid.
Explanation :
- When a liquid flows, it is considered to be moving in different layers in contact with one another.
- There is a force of friction between the adjacent layers of a moving liquid which opposes the motion of the liquid.
- When a liquid flows over a fixed surface, the layer of the molecules in the immediate contact of the surface experiences maximum friction and it is considered stationary.
- As the distance of upper layers increases from the fixed layer the velocity increases. Hence, there is a regular gradation of velocity of moving liquid layers from one layer to the next, and this flow is called laminar flow.
Question 5. Solve the following
(A) A balloon is inflated with helium gas at room temperature of 25 0C and at 1 bar pressure when its initial volume is 2.27 L and allowed to rise in air. As it rises in the air external pressure decreases and the volume of the gas increases till finally it bursts when external pressure is 0.3 bar. What is the limit at which volume of the balloon can stay inflated ?
T = 273 + 25 = 298 K
P1 = 1 bar; V1 = 2.27 L, P2 = 0.3 bar; V2 = ?
P1 × V1 = P2 × V2
∴ V2 = \(\frac{P_1V_1}{P_2}\) = \(\frac{1×2.27}{0.3}\) = 7.567 L
Limit of volume of balloon that can stay inflated = 7.567 L
(B) A syringe has a volume of 10.0 cm3 at pressure 1 atm. If you plug the end so that no gas can escape and push the plunger down, what must be the final volume to change the pressure to 3.5 atm?
V1 = 10 cm3; P1 = 1 atm, P2 = 3.5 atm; V2 =?
P1 × V1 = P2 × V2
∴ V2 = \(\frac{P_1V_1}{P_2}\) = \(\frac{1×10}{3.5}\) = 2.857 atm
Final pressure = 2.857 atm.
(C) The volume of a given mass of a gas at 0 0C is 2 dm3. Calculate the new volume of the gas at constant pressure when
(a) The temperature is increased by 10 0C.
(b) The temperature is decreased by10 0C.
(a) V1 = 2 dm3; T1 = 273 + 0 = 273 K, T2 = 273 + 10 = 283 K; V2 =?
\(\frac{V_2}{T_2}\) = \(\frac{V_1}{T_1}\)
∴ V2 = \(\frac{V_1T_2}{T_1}\) = \(\frac{2×283}{273}\) = 2.073 dm3
Volume of a gas = 2.073 dm3.
(b) V1 = 2 dm3; T1 = 273 K, T2 = 273 - 10 = 263 K; V2 =?
\(\frac{V_2}{T_2}\) = \(\frac{V_1}{T_1}\)
∴ V2 = \(\frac{V_1T_2}{T_1}\) = \(\frac{2×263}{273}\) = 1.927 dm3
Volume of a gas = 1.927 dm3.
(D) A hot air balloon has a volume of 2800 m3 at 99 0C. What is the volume if the air cools to 80 0C?
V1 = 2800 m3; T1 = 273 + 99 = 372 K, T2 = 273 + 80 = 353 K; V2 =?
\(\frac{V_2}{T_2}\) = \(\frac{V_1}{T_1}\)
∴ V2 = \(\frac{V_1T_2}{T_1}\) = \(\frac{2800×353}{372}\) = 2657 m3
(E) At 0 0C, a gas occupies 22.4 liters. How nuch hot must be the gas in Celsius and in kelvin to reach volume of 25.0 literes?
V1 = 22.4 L; T1 = 273 + 0 = 273 K, V2 = 25 L T2 =?
\(\frac{V_2}{T_2}\) = \(\frac{V_1}{T_1}\)
∴ T2 = \(\frac{V_2T_1}{V_1}\) = \(\frac{25×273}{22.4}\) = 304.7 K
∴ t2 = 304.7 - 273 = 31.7 C
T2 = 304.7 K; t2 = 31.7 C.
(F) A 20 L container holds 0.650 mol of He gas at 37 0C at a pressure of 628.3 bar. What will be new pressure inside the container if the volume is reduced to 12 L. The temperature is increased to 177 0C and 1.25 mol of additional He gas was added to it?
Initial conditions:
Volume V1 = 20 L, Temperature T1 = 37 0C = 273 + 37 = 310 K
Moles of He gas n1 = 0.650 mol, Pressure P1 = 628.3 bar
Final conditions:
Volume V2 = 12 L, Temperature T2 = 177 0C = 273 + 177 = 450 K
Total moles of He gas n2 = 0.650 mol + 1.25 mol = 1.9 mol
Using the ideal gas law PV=nRT, we can write:
P1V1 = n1RT1 and P2V2 = n2RT2
Since R (the gas constant) is the same, we get:
\(\frac{P_1V_1}{n_1T_1}\) = \(\frac{P_2V_2}{n_2T_2}\)
Now, solving for the final pressure P2:
P2 = \(\frac{P_1V_1n_2T_2}{n_1T_1V_2}\)
Substituting the values:
P2 = \(\frac{628.3×20×1.9×450}{0.650×310×12}\)
P2 ≈ 4443 bar = 4443 x 0.987 atm = 4385 atm
The new pressure inside the container would be approximately 4443 bar = 4385 atm.
(G) Nitrogen gas is filled in a container of volume 2.32 L at 32 0C and 4.7 atm pressure. Calculate the number of moles of the gas.
V = 2.31 L; T = 273 + 32 = 305 K, P = 4.7 atm; n = ?
PV = nRT
∴ n = \(\frac{PV}{RT}\) = \(\frac{4.7×2.31}{0.0821×305}\) = 0.4354 mol
Number of moles of the gas = 0.4354 mol.
(H) At 25 0C and 760 mm of Hg pressure a gas occupies 600 mL volume. What will be its pressure at the height where temperature is 10 0C and volume of the gas 640 mL ?
P1 = 760 mm, V1 = 600 mL, T1 = 273 + 25 = 298 K
V2 = 640 mL; T2 = 273 + 10 = 283 K; P2 = ?
\(\frac{P_1V_1}{T_1}\) = \(\frac{P_2V_2}{T_2}\)
∴ P2 = \(\frac{P_1V_1T_2}{T_1V_2}\) = \(\frac{760×600×283}{298×640}\) = 676.6 mm Hg
Pressure of gas = 676.6 mm Hg.
(I) A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5 g neon. If pressure of the mixture of the gases in the cylinder is 25 bar. What is the partial pressure of dioxygen and neon in the mixture?
mO2 = 70.6 g, MO2 = 32 g mol-1;
mNe = 167.5g, MNe = 20.18 g mol-1
PTotal = 25 bar
PO2 = ? PNe =?
nO2 = \(\frac{m_{O_2}}{M_{O_2}}\) = \(\frac{70.6}{32}\) = 2.206 mol
nNe = \(\frac{m_{Ne}}{M_{Ne}}\) = \(\frac{167.5}{20.18}\) = 8.3 mol
Total number of moles = 2.206 + 8.3 = 10.506 mol
Mole fractions :
xO2 = \(\frac{2.206}{10.506}\) = 0.2099
xNe = \(\frac{8.3}{10.506}\) = 0.79
Partial pressures :
PO2 = xO2 x PTotal = 0.2099 x 25 = 5.247 bar
PNe = xNe x PTotal = 0.79 x 25 = 19.75 bar
Partial pressure of O2(g) = 5.247 bar.
Partial pressure of Ne(g) = 19.75 bar.
(J) Calculate the pressure in atm of 1.0 mole of helium in a 2.0 dm3 container at 20.0 0C.
n = 1 mol; V = 2.0 dm3; T = 273 + 20 = 293 K P = ?
PV = nRT
∴ P = \(\frac{nRT}{V}\) = \(\frac{1×0.0821×293}{2.0}\) = 12.02 atm
Pressure = 12.02 atm.
(K) Calculate the volume of 1 mole of a gas at exactly 20 0C at a pressure of 101.35 kPa.
n = 1 mol; T = 273 + 20 = 293 K, P = 101.35 kPa = 101.35 x 103 Pa,
V =?
PV = nRT
V = \(\frac{nRT}{P}\) = \(\frac{1×8.314×293}{101.35}\) = 24.035 × 10-3 m3
= 24.035 dm3
Volume of the gas = 24.035 dm3.
(L) Calculate the number of molecules of methane in 0.50 m3 of the gas at a pressure of 2.0 × 102 kPa and a temperature of exactly 300 K.
P = 2 x 102 kPa = 2 x 105 Pa; V = 0.50 m3 , T = 300 K; n = ?
Number of molecules = ?
PV = nRT
∴ nCH4 = \(\frac{PV}{RT}\) = \(\frac{2×10^2×0.50}{8.314×300}\) = 40 mol
∴ Number of molecules = nCH4 x NA
= 40 × 6.02 × 1023
= 2.408 × 1025
Number of molecules of CH4 = 2.408 x 1025
PDF : Class-11-Chemistry-Chapter-10-States of Matter : Gaseous and Liquid States- Notes
PDF : Class-11-Chemistry-Chapter-10-States of Matter : Gaseous and Liquid States-Solution
All 16 Chapters Notes -11-Chemistry-(16 PDF) Rs.132
All 16 Chapters-Solutions-11-Chemistry- (16 PDF) Rs.128
All 16 Chapters-Notes+Solutions-11-Chemistry- (32 PDF) Rs.228
Main Page : – Maharashtra Board Class 11th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-9-Elements of Group 13, 14 and 15 – Online Solutions
Next Chapter : Chapter-11-Adsorption and Colloids – Online Solutions