Laws of Motion
Maharashtra Board-Class-11-Science-Physics-Chapter-4
Notes-Part-1
|
Topics to be Learn : Part-1
|
| Let’s recall :
Different types of motions : Linear motion
Non-linear motion
Kinematics : Motion with respect to space and time, ignoring the cause of that motion, is known as kinematics. Kinematics equations are a set of equations that can derive an unknown aspect of a body’s motion if the other aspects are provided. These equations link five kinematic variables: Displacement (Δx), Initial velocity (v0 ), Final velocity (v), Time interval (t) Constant acceleration (a) There are four basic kinematics equations: v = v0 + at Δx = \((\frac{v+v_0}{2})t\) Δx = v0t + ½ at2 v2 = v02 + 2a Δx |
Introduction to dynamics:
Science of mechanics : Mechanics or classical mechanics or Newtonian mechanics is the branch of Physics that deals with the motion of bodies in space, and with the forces of nature which cause or tend to cause this motion.
Branches of mechanics :
There are basically two branches of mechanics
- Statics : It is the study of objects at rest or in equilibrium under the action of balanced forces
- Kinetics : It is the study of bodies with actual motion.
Kinetics can be further divided into two branches
- Kinematics — It is the study of motion of bodies without reference to the forces affecting the motion
- Dynamics — It is the study of the relationship of motion to the forces that cause it.
Motion is a relative concept : Motion is a relative concept. In saying that something is moving, what is meant or implied is that its position relative to something else is changing with time. It should always be described in context to a reference frame.
Trajectory of a particle :
Trajectory of any motion is decided by acceleration \(\vec{a}\) and the initial velocity \(\vec{u}\) .
(i) Trajectory of a particle when, the particle is at rest and is given an acceleration which is constant in direction :
- Rectilinear, i.e., one-dimensional, motion. The particle will move with an increasing speed in the direction of the acceleration.
(ii) Trajectory of a particle when, the particle has a non-zero velocity \(\vec{u}\) and is given an acceleration along ± \(\vec{u}\) :
- Rectilinear, i.e., one-dimensional, motion. If the acceleration \(\vec{a}\) is in the direction of \(\vec{u}\) the particle will move with an increasing speed in the direction of the acceleration. If \(\vec{a}\) is in the direction of \(-\vec{a}\), the particle will decelerate, come to a momentary stop and move in the opposite direction with increasing speed.
(iii) Trajectory of a particle when, the particle has a non-zero velocity and an acceleration that is always perpendicular to the velocity and constant in magnitude :
- Uniform circular motion, in the plane containing the velocity and acceleration vectors.
(iv) Trajectory of a particle when, the particle has a non-zero velocity that is not along its acceleration which is constant in magnitude and direction :
- Parabolic motion, in the plane containing the velocity and acceleration vectors.
Aristotle’s Fallacy:
Aristotle stated that “an external force is required to keep a body in uniform motion”.
Explanation : From our daily experience, we know that a push is required to roll a ball, or to slide a heavy object, on a horizontal surface. Aristotle taught that an external force presumably acts on the object for as long as it continues its motion, and the motion stops when the force ceases. That is, a force is the cause of, or necessary for, continued motion.
Q. Was Aristotle correct? If correct, explain his statement with an illustration. If wrong, give the correct modified version of his statement.
Ans. Aristotelian doctrine that an external force is the cause of continued motion against "natural tendency” was incorrect. Since it is a wrong opinion based on a flawed reasoning, it is called a fallacy.
In the observation of a ball rolling on a horizontal floor eventually coming to a stop, correct explanation to Aristotle’s fallacy was first given by Galileo, which was later used by Newton in formulating laws of motion. Galileo showed that all the objects stop moving because of some resistive or opposing forces like friction, viscous drag, etc. Thus, an external force is not the cause of motion of an object but for a change in its motion. For its continued motion, an external force is required to overcome these resistive forces.
Newton’s Laws of Motion:
First Law : Every material body continues in its state of rest, or of uniform motion in a straight line, unless it is acted upon by an external force.
Second Law : The rate of change of momentum of a body is proportional to the resultant applied force, and takes place in the direction of the force.
Third Law : To every action (force) there is always an equal (in magnitude) and opposite (in direction) reaction (force). OR
Action and reaction are always equal in magnitude and opposite in direction, and act on contrary parts.
Inertia : Inertia is the property of matter that causes it to resist any change in its motion. The mass of a body is a measure of its inertia. The greater the mass of a body, the greater is its inertia (i.e., the smaller the acceleration it has for a given force).
- The first law is also called the law of inertia because it ascribes to bodies the properties of being inert, i.e., of requiring the action of a force for their acceleration
Momentum : Momentum of a body is defined as the product of its mass and velocity.
- It is a vector quantity.
- Dimensions: [LMT-1]
- SI unit : kg-m/s
Discussion : Newton's first law of motion defines force while the second law measures it.
Newton's first law of motion gives, qualitatively, the relation between force and motion.
We know that there is a force \(\vec{F}\) at work (more precisely, a resultant or unbalanced force) only when a particle's velocity changes, i.e., it has an acceleration \(\vec{a}\). Thus, force is that physical quantity which causes acceleration.
An acceleration of one body is to be associated with the presence of one or more other bodies mutually interacting with it.
Then, according to Newton's first law of motion, if \(\vec{F}\) = 0, \(\vec{a}\) = 0. In other words, if a body is observed to be at rest or to move uniformly in a straight line, either there are no other bodies mutually interacting with it, or the other bodies are so positioned that they produce at all times a resultant acceleration of zero.
Newton's second law gives a quantitative measure of a force : \(\vec{F}=\frac{dv}{dt}\) = \(m\vec{a}\)
, where m ≡ mass of the body assumed to be constant and \(\vec{p}\) ≡ momentum.
We then define the SI unit of force, the newton, as that force which produces an acceleration of 1 m/s2 in a body of mass 1 kg.
Thus, Newton’s first law of motion defines force and the second law measures it.
Importance of Newton's first law of motion :
- It shows an equivalence between ‘state of rest’ and ‘state of uniform motion along a straight line’ as both need a net unbalanced force to change the state. Both these are referred to as ‘state of motion’. The distinction between state of rest and uniform motion lies in the choice of the ‘frame of reference’. Newton's first law thus defines inertial frames of reference in which all the three laws hold.
- It qualitatively defines force as a physical quantity that causes acceleration.
- It ascribes to a material body a fundamental property called inertia that causes the body to resist any change in its motion.
Importance of Newton's second law of motion :
- It provides a quantitative measure of force.
- Newton’s own version of the second law, \(\vec{dp}\) = \(\vec{F}dt\), where is the net force acting on a body, recognized momentum as a more useful concept in developing the science of dynamics.
Importance of Newton's third law of motion :
- Newton's laws assume that the force on a body has its origin in other bodies, i.e., bodies have an influence on one another, which we attribute to an entity called force. Newton's third law of motion says that this influence is mutual: one body cannot influence another without itself being affected by that body.
- Action and reaction forces are always on different objects, i.e. an isolated force does not exist. Forces act always in pairs, and simultaneously. Any of the pair can be called as action and the other as reaction. However, a given pair act on the two different interacting bodies; hence, they do not cancel each other.
Discussion : Newton's first law of motion can be deduced from his second law.
By Newton's second law of motion, \(\vec{dp}\) = \(\vec{F}dt\) , where \(\vec{dp}\) is the change in momentum of a body in time dt when a net force is acting on the body.
If the mass of the body is constant,
\(\vec{dp} = d(m\vec{v})\) = \(md\vec{v}\)
So that, if \(\vec{F}\) = 0, \(\vec{v}\) is constant, Hence if there is no force, velocity will not change. This is nothing but Newton’s first law of motion.
| Know This :
Mathematical expression for force must be remembered as \(\vec{F}=\frac{\vec{dp}}{dt}\) and not as \(\vec{F}\) = \(m\vec{a}\) \(\vec{F}=\frac{\vec{dp}}{dt}=\frac{d(m\vec{v})}{dt}\) = \(\frac{dm}{dt}(\vec{v})+m\frac{\vec{dv}}{dt}\) = \(\frac{dm}{dt}(\vec{v})+m\vec{a}\) For a given body, mass is constant, i.e., \(\frac{dm}{dt}\) = 0 and only in this case, \(\vec{F}\) = \(m\vec{a}\)
|
Inertial and Non-Inertial Frames of Reference :
Inertial Frames of Reference : An inertial frame of reference is one in which Newton's laws of motion hold. Newton's laws assume that bodies have mutual influence (action and reaction) on one another. Then, Newton's first law says that the natural (uninfluenced) state of every body is one of constant velocity, including zero.
Motion can only be described with respect to a frame of reference, i.e., with respect to other bodies. Therefore, a body can have constant velocity if the reference bodies forming the surrounding produce no acceleration of the body. A system of bodies providing such a frame of reference is called an inertial frame of reference, because in it the law of inertia holds.
But the first law mentions "every" body; that is, if we fix up a frame of reference for a body in which it is in its natural state, then every uninfluenced body will move uniformly in the same frame of reference.
Thus, an inertial frame of reference is one in which every free body, i.e., uninfluenced body, moves with constant velocity, including zero.
Newton's laws of motion are applicable only in an inertial frame of reference that the laws themselves define.
A frame of reference which itself has uniform motion in a straight line with respect to an inertial frame of reference is also an inertial frame. All inertial frames are equivalent, i.e., if a body has zero acceleration in one inertial frame of reference, it has zero acceleration in every other inertial frame.
Non-Inertial Frames of Reference :
An accelerated frame of reference, that is, one which has an acceleration with respect to an inertial frame of reference, is called a noninertial frame of reference.
Examples :
- A frame of reference that is moving in a straight line with an acceleration with respect to an inertial frame
- A frame of reference that is rotating with respect to an inertial frame.
Remember :
- Newton's laws are obeyed in an inertial frame.
- Newton's laws are not obeyed in a noninertial frame.
- In inertial frame, any force acting on a body is a real force.
- In a noninertial frame, the acceleration of the frame gives rise to a pseudo force.
Limitation of Newton’s laws of motion :
- Newton’s laws are applicable only in the inertial frames of reference which they define. If the body is in a frame of reference of acceleration (a), we need to use a pseudo force (−m\(\vec{a}\) ) in addition to all the other forces while writing the force equations.
- Newton’s laws are applicable for point objects.
- Newton’s laws are applicable to rigid bodies. A body is said to be rigid if the relative distances between its particles do not change for any deforming force.
- For objects moving with speeds comparable to that of light, Newton’s laws of motion do not give results that match with the experimental results and Einstein's special theory of relativity has to be used.
- Behaviour and interaction of objects having atomic or molecular sizes cannot be explained using Newton’s laws of motion, and quantum mechanics has to be used.
Types of Forces:
Fundamental Forces in Nature:
All the forces in nature are classified into following four interactions that are termed as fundamental forces.
- Gravitational force
- Electromagnetic force
- Strong nuclear force
- Weak nuclear force.
Ranges and Relative Strength :
- The gravitational force and the electromagnetic force are long-range forces, extending, in principle, to infinity.
- Both the strong nuclear force and the weak nuclear force are extremely short-range forces; the strong nuclear force becomes essentially zero for separations between neutrons and protons (collectively referred to as nucleons) greater than about 3 x 10−15 m, and the weak nuclear force within a nucleon has a range of about 10−8 m.
- In relative strength, the strong nuclear force is the strongest of the four while the gravitational force is the weakest : gravitational force < weak nuclear force < electromagnetic force < strong nuclear force.
(1) Gravitational force : The gravitational interaction is an attraction between any two bodies in the universe and has its origin in the intrinsic property of matter called mass.
Newton's law of universal gravitation states that every particle of matter in the universe attracts every other particle with a force which is directly proportional to the product of their masses, inversely proportional to the square of the distance between them and acts along the line joining them.
For two particles of masses m1 and m2 separated by a distance r, the magnitude of the gravitational force between them is
F ∝ \(\frac{m_1m_2}{r^2}\)
∴ F = \(G\frac{m_1m_2}{r^2}\)
where G is called the universal gravitational constant and is of the order of 10−10 (in SI units).
The gravitational pull of the Earth acts as if all its matter were concentrated at its centre; so, for all bodies on the Earth's surface, r in the above equation is the radius of the Earth. The gravitational pulls of the Sun and Moon cause the ocean tides.
Characteristics :
- It is an attractive force and obeys the inverse square law of distance.
- It does not depend on the intervening medium.
- Gravity is a very weak but long-range interaction. It is because G is so small that it is hard to measure it and makes gravity the weakest of the four basic forces in nature.
- Because gravity is so weak, it is of importance only when the interacting bodies are uncharged and at least one of the bodies is very massive, i.e., of astronomical size.
- Because it is always of attraction and the celestial bodies are practically uncharged it is responsible for the large scale structure of the universe.
(2) Electromagnetic force : It is an attractive or repulsive force between electrically charged particles.
- The electromagnetic interaction has its origin in an intrinsic property of matter called electric charge. The electromagnetic force has two facets, electric and magnetic. Between a pair of charged particles there are electric forces, in addition to the ever present weak force of gravity.
- Furthermore, when charges are in relative motion, an additional magnetic force comes into play. Electric forces act even when the charges are at rest. In contrast, magnetic forces arise exclusively from charges in relative motion and are velocity dependent. The electron/proton spin plays an important role in magnetic interaction.
- Majority of forces experienced in our daily life, such as force of friction, normal reaction, tension in strings, collision forces, elastic forces, viscosity (fluid friction), etc. are EM in nature.
- Under the action of these forces, there is deformation of objects that changes intermolecular distances thereby resulting into reaction forces.
Characteristics :
- Electric force can be attractive or repulsive but obeys the inverse square law of distance.
- Electromagnetic forces depend on the intervening medium.
- They are long-range forces.
- They act only when both the interacting bodies are charged and then they are enormously greater than the gravitational force between these bodies.
(3) Strong (nuclear) force: This is the strongest force that binds the nucleons together inside a nucleus.
- Though strongest, it is a short range (<10−14 m) force. Therefore is very strong attractive force and is charge independent.
- Since a nucleus consists of positively charged protons and neutral neutrons, the electric forces inside the nucleus are all repulsive, tending to break the nucleus.
- Existence of stable nuclei shows that an additional attractive charge-independent force must be present in nuclei to counteract the Coulomb repulsion between protons.
Characteristics :
- It is attractive and the strongest of the basic forces in nature.
- The strong interaction is an extremely short- range force, effective only at separations of about 10−15 m, i.e., only within a nucleus. At the subnuclear distances involved, it is the dominant force — about 102 times stronger than the electromagnetic force.
- Beyond about 3 x 10−15 m, the force is essentially zero, decreasing with distance much more rapidly than the inverse-square behavior of the gravitational and the electromagnetic interaction.
- At the subnuclear distances involved, it is an attractive force which acts between all pairs of nucleons, i.e., between proton and neutron, between proton and proton, and between neutron and neutron. That is, it is charge independent and its properties determine the structure of nuclei.
Weak (nuclear) force: This is the interaction between subatomic particles that is responsible for the radioactive decay of atoms, in particular beta emission.
Its role in the structure of matter is to make unstable nuclei, i.e., nuclei with high neutron/proton ratios, undergo beta decays reducing the n/p ratio.
Characteristics :
- The weak nuclear force is an extremely short-range force, effective only within a nucleon (~ 10−18 m).
- It exists between all pairs of subatomic particles : While it is the exclusive force between an electron and an antineutrino, the same force also exists between two protons. In the latter case, it is overwhelmed by the electric repulsion and strong nuclear attraction.
- The weak nuclear force is not as weak as the gravitational force, but much weaker than the strong nuclear and EM forces.
| Know This :
Weak interaction force:
|
Contact and Non-Contact Forces:
Forces can be grouped into two categories :
Contact forces :
- These are due to direct physical contact between interacting objects.
- Normal force (or normal reaction), forces exerted during collision, spring force, tension in a string, forces of solid and fluid friction are all examples of contact force. A normal force is the force exerted by a surface against an object that is pressing against the surface.
- Contact forces are fundamentally electromagnetic. However, in the context of Newtonian mechanics, their electromagnetic origin is not an important concern.
Non-contact forces :
- They act without the necessity of physical contact between interacting objects.
- All four fundamental forces of nature, namely, gravitational, electromagnetic, strong and weak, are non-contact interactions.
Real and Pseudo Forces:
Real force ; A real or true force is one whose origin can be traced to any of the four basic interactions between matter.
Examples ; The muscular force exerted to lift an object or to cause the usual push and pull, the frictional force that allows us to walk, the elastic force in a spring, the force that the atmosphere exerts on the mercury in a barometer, the force that the Moon exerts on the Earth to cause the tides, the electromagnetic forces that turn the fan motor, the hydraulic force that operates brakes and carlifts, the mechanical force on a ball when a batsman hits out with his bat. These are all gravitational or electromagnetic in origin.
Pseudo force : A pseudo force or a fictitious force is one which arises due, not to any of the basic interactions between matter but, to the acceleration of the observer's frame of reference.
Pseudo does not mean imaginary (because these are measurable with instruments) but just means non-real.
Examples : The outward centrifugal force on a body at rest in a rotating frame of reference, e.g., on a person in a car going around a curve.
The sideways Coriolis force appears to act on a body in a rotating reference frame only if the body is moving relative to that reference frame.
Concept of pseudo force in a non-inertial frame of reference :
Suppose a particle of mass m has an acceleration gas measured in an inertial frame of reference S. Use of Newton's laws would correctly attribute this to a real force \(\vec{F}=m\vec{a}\) .
However, the particle is at rest in a frame S’ attached to it. Newton's laws can explain the state of rest of the particle in S’ provided a force —mg (in the opposite direction to the acceleration of the frame S’ is introduced. This pseudo force exists only in frame S’ and is measurable in S’. It originates not from any interaction with another body but purely from the acceleration of the frame of reference.
For example, when a vehicle or elevator is accelerating, a person at rest inside feels a force opposite to the direction of the person's accelerated frame of reference.
Some pseudo forces are given special names.
For example, if a particle is at rest in a frame S’ which is rotating with respect to S, then the force \(-m\vec{a}\) in S’ is called the centrifugal force. If, in addition, the particle moves with a constant velocity in such a frame S’ then there is an additional sideways force on the particle called the Coriolis force.
All the above pseudo forces are also non-Newtonian forces because Newton's third law of motion does not apply to them — there is no reaction force to them, i.e., no equal and opposite force acting on some other body.
Conservative and Non-Conservative Forces and Concept of Potential Energy:
Work done by a constant force :
The work done on a body by a constant force (constant in both magnitude and direction) is defined to be the product of the magnitude of the displacement of the body times the component of the force parallel to the displacement.
Suppose a constant force acting on a body displaces it by \(\vec{s}\). Then, the work done by the force is
W = \(\vec{F}.\vec{s}\) = (F cos θ)s
where θ is the smaller angle between |(\vec{F}\) and \(\vec{s}\) and so that F cos θ is the component of the force in the direction of the displacement. In rectangular component form,
W = Fxsx + Fysy + Fzsz
- Work done is a scalar quantity.
- SI unit : the joule (J); 1 J = 1 N.m.
- CGS unit : the erg; 1 erg = 1 dyn.cm.
- Dimensions : [ML2T−2]
Concept of work done by a variable force :
Suppose a body (particle) is displaced in the + x-direction under the action of a force, also in the + x-direction but whose magnitude changes as the body moves. (see Figure) is a graph of the force as a function of the particle's coordinate x.
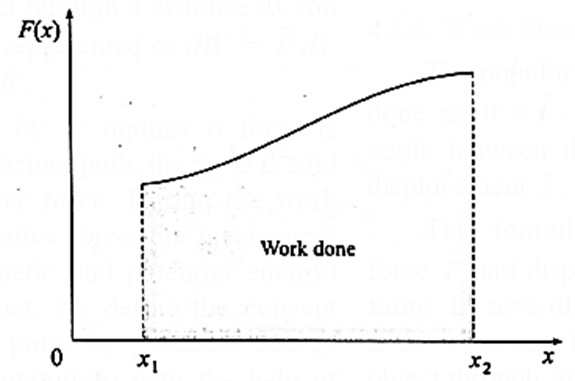
If the body moves along the x-axis from point x1 to x2, the work done by the varying force for this displacement is given by the area under the curve, as shown. In the notation of integral calculus, the work done
W = \(\int \limits_{x_1}^{x_2}Fdx\)
where the right hand side is the definite integral over the limits x = x1 and x = x2.
If the force is not in the direction of the displacement — for example, a body moving from point A to B acted on by a force \(\vec{F}\) that varies in magnitude and direction (see below Fig.), then at every instant we must consider the component of the force iin the direction parallel to the displacement
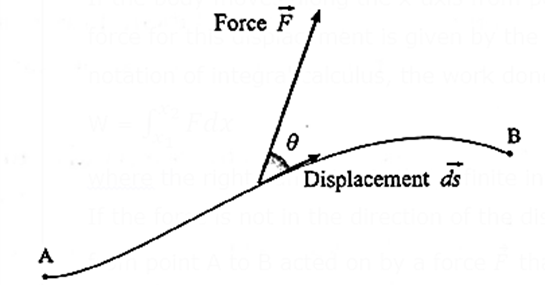
Let \(\vec{F}\) be the force at a point along the path, and let θ be the angle between \(\vec{F}\) and \(\vec{s}\) at this point. Then, the work done during the displacement \(\vec{ds}\) is
dW = (F cos θ) ds = \(\vec{F}.\vec{ds}\)
Then, W = \(\int \limits_{A}^{B} dW\) =\(\int \limits_{A}^{B}\vec{F}.\vec{ds}\)
This is the formula for calculating work done by variable force.
Note : The formula W = \(\vec{F}.\vec{ds}\) = (F cos θ)s is applicable only if \(\vec{F}\) is constant, both in magnitude and direction, over the displacement
If the force varies in magnitude and/or direction, then we must consider dW = \(\vec{F}.\vec{ds}\) during an infinitesimal displacement \(\vec{ds}\) in an infinitesimal time interval dt→0. The total work done by the variable force in moving the body from point A to point B is given by the integrating dW over the path from A to B.
W = \(\int \limits_{A}^{B} dW\) =\(\int \limits_{A}^{B}\vec{F}.\vec{ds}\)
Graphically, we plot the component of \(\vec{F}\) parallel to the direction of the motion at a point as a function of the displacement. Then, the total work is given by the area under the curve between the initial and final points.
Expression for the power delivered by the force in terms of F, m and t when a constant force \(\vec{F}\) acts on a body of mass m, initially at rest, for time t :
The power P delivered by a force is the time rate of work done by the force :
P = dW/dt
Under the action of a constant force \(\vec{F}\) if the displacement of the body in an infinitesimal time interval dt is \(\vec{ds}\) , the infinitesimal work done by the force in this time dt is
dW = \(\vec{F}.\vec{ds}\)
∴ P = \(\vec{F}.\frac{\vec{ds}}{dt}\) = \(\vec{F}.\vec{v}\) = Fv cos θ
Since F is constant, the acceleration \(\vec{a}=\frac{\vec{F}}{m}\) is also constant.
∴ \(\vec{v}=\vec{u}+\vec{a}t\) = \(\vec{a}t\) ('.'u = 0)
∴ \(\vec{v}= \frac{\vec{F}}{m}t\)
∴ P = \(\vec{F}.\frac{\vec{F}}{m}t\)=\(\frac{F^2m}{t}\) is the required expression.
Dimensions : [Power] =[work]/[time]=[ML2T-2]/[T] = ML2T-3
SI Unit : The Watt = the joule per second (1 W = 1 J/s)
Conservative force :
The force required to move a body from one point to another is called a conservative force if the work done in moving the body between these points is independent of the path taken.
Explanation :
For example, suppose only a conservative force facts on a particle as it moves from point A to point B along either path 1 or path 2, see above Fig.(a). Then the work done on the particle is the same along the two paths.
WAB, path1 = \(\int \limits_{A,path1}^{B}\vec{F}.\vec{ds}\) = WAB, path2 = \(\int \limits_{A,path2}^{B}\vec{F}.\vec{ds}\)
If the particle moves from A and eventually returns to that position, i.e., the particle moves along a closed path beginning and ending at the initial position, then the total work done by the conservative force during the round trip along this and any other closed path is zero.
Thus, the net work done by a conservative force on a particle around every closed path is zero.
W closed path = \(\oint \vec{F}.\vec{ds} \)
The above two equations are equivalent because any closed path is the sum of two paths : the first going from A to B, and the second going from B to A, Fig.(b), where
A and B are any two points on the closed path,
The work done in going along a path from B to A is the negative of the work done in going along the same path from A to B.
\(\oint \vec{F}.\vec{ds} \) = \(\int \limits_{A,path1}^{B}\vec{F}.\vec{ds}\) + \(\int \limits_{B,path2}^{A}\vec{F}.\vec{ds}\)
= \(\int \limits_{A,path1}^{B}\vec{F}.\vec{ds} - \int \limits_{A,path2}^{B}\vec{F}.\vec{ds}\)
In the field of a conservative force, the total energy of the particle — kinetic plus potential — at any two points is the same, i.e., it is conserved.
Important examples of conservative forces are gravity and the static electric force. The force of an ideal spring — fundamentally an electric force — is also conservative.
Non—conservative force :
A force that is not conservative is called a non-conservative force. A non-onservative force is a dissipative force. The work done by a non-conservative force is lost and cannot be converted into useful work later.
- Example : A kinetic frictional force and force due to air resistance are non-conservative forces.
Concept of potential energy in the field of a conservative force : Work done against a conservative force is stored in the sense that we can get it back again in the form of kinetic energy. We consider the ”stored work” as potential energy U, in the sense that it can be released as kinetic energy. Changes in potential energy are all that ever matter physically. Hence, we define change in potential energy formally in terms of the work done by a conservative force. The change in potential energy associated with a conservative force is the negative of the work done by that force as it acts over any path from point A to point B : ΔUAB = \(-\int \limits_{A}^{B}\vec{F}.\vec{ds}\) The minus sign indicates that if a conservative force does positive work (as does gravity on a falling object), then potential energy of the system must decrease, i.e., ΔU must be negative. Conversely, if a conservative force does negative work (as does gravity on an object being lifted), then energy is stored in the system and potential energy must increase, i.e., ΔU must be positive. When force and displacement are parallel or antiparallel, the above equation simplifies to ΔUAB = \(-\int \limits_{x_1}^{x_2}F(x)dx\) where x1 and x2 are the starting and ending points on the x-axis, taken to coincide with the path. If the force is constant during this displacement, ΔUAB = −F(x2 − x1) We usually drop the subscripts AB and write simply All for a change in potential energy. Keeping the subscript is important, though, when we need to be clear about whether we are going from A to B or from B to A. Since integration is the inverse operation of differentiation, we can as well start with the potential energy and take its derivative, with respect to displacement, to get the force. The infinitesimal increment of potential energy is the dot product of the force \(\vec{F}\) and the infinitesimal displacement \(d\vec{l}\) dU = \(-\vec{F}.d\vec{l}\) = −Fl dl where Fl, is the component of \(\vec{F}\) in the direction of the displacement. This equation gives the relation between force and the potential energy associated with it. That is, the component of a conservative force, in a particular direction, equals the negative of the derivative of the corresponding potential energy with respect to a displacement in that direction
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 3: Motion in a Plane – Online Notes
Next Chapter : Chapter 5: Gravitation – Online Notes
I want the notes of laws of motion class 11center of mass
I want to law of motion notes class 11 center of mass
visit pdf store to buy pdf.