Notes-Class-11-Science-Physics-Chapter-6-Mechanical Properties of Solids-Maharashtra Board

Topics to be Learn : Part-1 Introduction Elastic behaviour of solids Stress and Strain Hooke’s law Elastic constants Stress-Strain curve Strain energy Hardness Friction in solids

Introduction:

Solids : Solids are made up of atoms or groups of atoms arranged in a specific geometric configuration.

Equilibrium conditions of solids :

• Nature has determined this arrangement so that the resultant force operating on each constituent as a consequence of others is zero. This is a solid's equilibrium condition at room temperature.
• The specified equilibrium arrangement remains constant over time. It can change only when an external stimulus, like compressive force from all sides, is given to a solid.
• Even at very low temperatures, the constituents vibrate about their equilibrium places but cannot leave their fixed positions.
• This fact gives solids a definite shape and size (allows solids to keep their definite shape and size).

Effect of applied force on solids :

• When a force is applied to a solid which is not free to move, the relative positions of its constituents (atoms and molecules) change, resulting in a change in the shape or size (volume) or both of the body.

 Deformation :

• A change in the shape or size(Volume) or both of a body due to an external force is called deformation.
• External balanced forces that produce a change in the shape or size or both of a body are called deforming forces.

Elastic Behavior of Solids:

Elasticity : If a body regains its original shape and size after removal of the deforming force, it is called an elastic body and the property is called elasticity.

• Materials with strong internal restoring forces possess this property.

• Examples of elastic materials are metals, rubber, quartz, etc.

 Perfectly elastic : If a body regains its original shape and size completely and instantaneously upon removal of the deforming force, then it is said to be perfectly elastic.

Plasticity : It is the property of a body or material due to which the body (or the material) does not regain its original shape and size but retains its altered shape and size after removal of the deforming force.

• Materials with weak internal restoring forces possess this property.

Plastic body : If a body does not regain its original shape and size but partly retains its altered shape and size even after removal of the deforming force, it is called a plastic body.

• Examples of plastic materials are clay, putty, plasticine, thick mud, etc.

Remember : There is no solid which is perfectly elastic or perfectly plastic. The best example of a near ideal elastic solid is quartz fibre and that of a plastic body is putty.

Stress and Strain:

Equilibrium state of deformed body :A deformed body is in equilibrium when the deforming force and the internal restoring force are equal in magnitude and opposite in direction.

Stress : Stress is defined as the net internal restoring force per unit area of the surface of a body over which the deforming force is applied.

• Internal restoring forces cannot be measured directly. So, in all cases, stress is measured as the applied force per unit area.

∴ Stress = \(\frac{internal\,\,restoring\,\,force}{area}\)=\(\frac{applied\,\,force}{area}\)

SI unit : The SI unit of force is the newton and that of area is square metre. Hence, the SI unit of stress is the newton per square metre.

The special name of this unit in SI is the pascal, in honour of Blaise Pascal (1623-62), French mathematician, physicist and philosopher.

1 Pa = 1 N/m²

Dimensions : [stress] = \(\frac{[force]}{[area]}\) = \(\frac{[M^1L^1T^{-2}]}{[area]}\)

Hence, the dimensions of stress are [L⁻¹M¹T⁻²]

Strain : Strain is defined as the ratio of change in dimensions of the body to its original dimensions i.e Strain is a measure of the deformation of a body.

Strain = \(\frac{change\,\,in\,\,dimensions}{original\,\,dimensions}\)

• When two equal and opposite forces are applied to an elastic body, there is a change in the dimensions of the body,
• The extent of the deformation is measured as the relative change in length, volume and/or shape.
• As strain is the ratio of two similar quantities, such as length or volume, it does not have unit and dimensions

Types of stresses and corresponding strains :

(1) Normal or longitudinal stress, which changes the length of a body. Longitudinal strain is the resulting fractional change in length of the body.

Definition and explanation:

(i) Normal or longitudinal stress : The normal or longitudinal stress is the normal force per unit area of cross section applied to a body that produces a change in the length of the body.

Explanation :

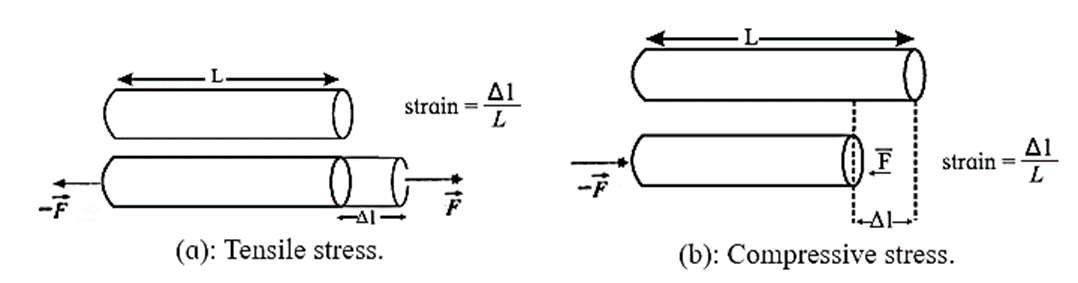
Consider a rod of uniform cross section A subjected to equal and opposite pulls \(\vec{F}\) and \(-\vec{F}\) at its ends.

• At a transverse section of the rod not too near its ends, these pulls are uniformly distributed over and perpendicular to the cross-sectional area A. Then the rod is said to be in tension.
• This produces an elongation in the rod and the length of the wire increases accordingly, as shown in Fig (a). This normal stress is called tensile stress
• If the rod is subjected to pushes at its ends, it is said to be under compression and the normal stress is called a compressive stress.

Normal (tensile or compressive) stress = F / A

(ii) The longitudinal (tensile or compressive) strain : It is the fractional change in the length of a body subjected to normal or longitudinal stress.

OR

The longitudinal strain is the ratio of the change in length to the original length of a body subjected to a normal or longitudinal stress.

Explanation :

Consider stretching (or compressing) a rod along its length which changes its length from L to L + ΔL, Fig. (a) ΔL is considered to be negative under compression, Fig. (b).

Then, tensile (or compressive) strain = \(\frac{change\,\,in\,\,length}{original\,\,length}=\frac{ΔL}{L}\)

(2) Volume stress, which changes the volume of a body without producing a change in its shape. Volume strain is the resulting fractional change in volume of the body.

Definition and explanation:

(i) Volume stress : The volume stress is the uniform force per unit surface area applied to a body that produces a change in the volume of the body.

Explanation :

Let \(\vec{F}\) be a force acting perpendicular to the entire surface of the body. It acts normally and uniformly all over the surface area A of the body. Such a stress which produces change in size but no change in shape is called volume stress.

Volume stress = F / A

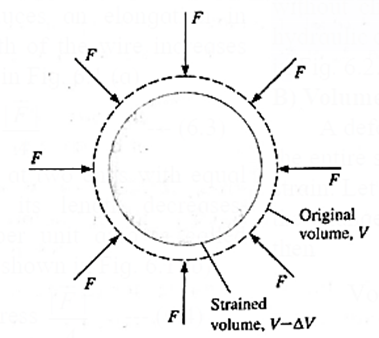
Volume stress produces change in size without change in shape of body, it is called hydraulic or hydrostatic volume stress as shown above fig

(ii) Volume strain : The volume or bulk strain is the fractional change in the volume of a body subjected to a volume stress. OR

The volume or bulk strain is the ratio of the change in volume to the original volume of a body subjected to a volume stress.

Explanation : If a body is subjected to a change in pressure from p to p + Δp, its volume will change from V to V + ΔV. If the body is submerged in a fluid and subjected to an increase in pressure (Δp positive), its volume will decrease (ΔV negative). Fig. Then,

Volume or bulk strain = \(\frac{change\,\,in\,\,volume}{original\,\,volume}=\frac{ΔV}{V}\)

(3) Shear stress, which changes the shape of a body. The corresponding strain is called the shear strain or shear.

Definition and explanation:

(i) Shear stress : The shear stress is the tangential force per unit area that tends to shear a body, i.e., to change its shape.

Explanation : Consider a rectangular block (a cuboid) with its bottom surface fixed, subjected to a force \(\vec{F}\)  tangential to the top surface of area A.

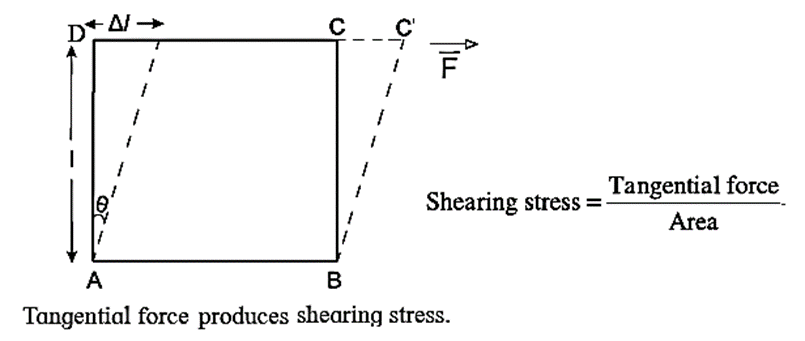
Then, each layer of the block, parallel to the top surface, is displaced in the direction of \(\vec{F}\). This changes the shape of the block.

Shear stress = F / A

(ii) Shear strain : The shear strain or shear is the ratio of the relative lateral displacement of two parallel layers of a body to the perpendicular distance between them when subjected to a shear stress.

Explanation : A rectangular block (a cuboid) subjected to shear stresses undergoes a change of shape to parallelepiped, above Fig. The resulting angular deformation (in radian), 9, at one corner is a measure of the shear.

Shear strain = \(\frac{\text{relative lateral displacement}}{\text{perpendicular distance between the two layers}}=\frac{Δl}{l}\)

= tan θ = θ  (in radian, and very small)

Remember : When a body is under a shear transformation, there is no change in area and volume. A rectangle is transformed into a parallelogram and a cuboid is transformed into a parallelepiped.

Know This : When a balloon is blown, its membrane experiences an outward pressure from within. This volume stress increases its volume. When the pressure (volume stress) exceeds the limit of bulk elasticity of the material, the balloon explodes. A gas cylinder too explodes for the same reason. A submerged submarine is under compressive volume stress and may implode if it goes to a greater depth than it is designed for.

Hooke’s Law:

Robert Hooke (1635-1703), physicist, studied the tension in a wire and strain produced in it. His study led to a law now known as Hooke’s law.

Hooke’s law : Within elastic limit, stress is directly proportional to strain.

Explanation : Within the elastic limit, stress ∝ strain, i.e. The relation between them is linear and the stress—strain graph is a straight line passing through the origin (0, 0), Fig.

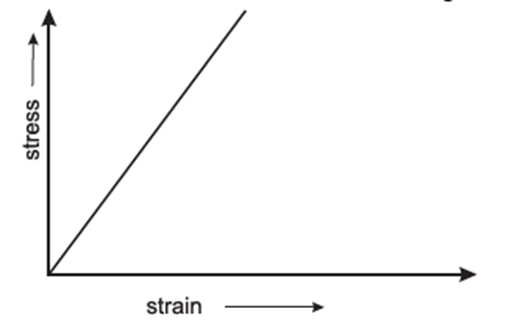
The slope of the linear region gives the constant of proportionality \(\frac{stress}{strain}\), called modulus of strain elasticity. It is a constant for a given material and for a given type of strain. Hence, a modulus of elasticity is called an elastic constant.

The conditions under which Hooke's law holds good :

• Hooke’s law holds good up to a limit till the deformation is elastic. Within this limit, the applied force (external force) is not very large.
• In an elastic deformation, the atoms/molecules of the body shift only a small fraction of an interatomic/intermolecular spacing in response to deforming forces and the internal restoring force is proportional to the strain produced by the applied force.

Elastic limit : The maximum value of stress up to which the stress developed in a body is directly proportional to the strain produced in it is called the elastic limit.

• It is slightly higher than the proportional limit, but beyond the proportional limit the stress-strain relation is no longer linear.

Modulus of elasticity : The modulus of elasticity is the ratio of stress to the corresponding strain of a material obeying Hooke’s law. It is the slope of the linear region of the stress versus strain graph.

Dimensions and SI unit of a modulus of elasticity :

Strain is a dimensionless quantity and has no unit. As such, its dimensions can be written as [M⁰ L⁰ T⁰].

∴ [modulus of elasticity] =  [ML⁻¹ T⁻²].

SI unit : the Pascal or the newton per square metre (Pa=N/m²)

Young's modulus (Y) : It is defined as the ratio of longitudinal stress to the corresponding longitudinal strain within the elastic limit.

• This modulus is named in honour of Thomas Young (1773-1829), British physiologist, physicist and Egyptologist.
• Young's modulus indicates the resistance (opposition) of an elastic solid to elongation or compression (contraction along the length).
• Young’s modulus of a material is useful for characterization of an object subjected to compression or tension.
• Young's modulus is the property of solids only.

Young's modulus of a rigid body : A perfectly rigid body cannot be deformed by any external force. Hence, there is no question of stress, strain and Young's modulus in this case.

• Remember : A perfectly rigid body does not exist in nature.

Young's modulus of some familiar materials :

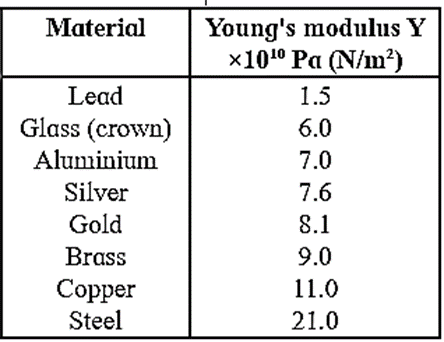
Bulk modulus : Bulk modulus is defined as the ratio of the volume stress to the corresponding volume strain.

• Bulk modulus indicates the resistance (opposition) of a solid or a liquid or a gas to compression (change in volume).
• Bulk modulus depends on temperature.

Compressibility : The reciprocal of bulk modulus of elasticity is called compressibility. OR. The ratio of the volume strain to the corresponding volume stress is called compressibility.

Compressibility, k = 1/K , where K is bulk modulus.

Dimensions : [k] = [M⁻¹LT²]

SI unit : Pa⁻¹ (=m²/N).

Shear modulus or modulus of rigidity (η) : Shear modulus or modulus of rigidity is defined as the ratio of shear stress to the corresponding shear strain, within the elastic limit.

• Modulus of rigidity indicates the resistance (opposition) of a solid to change in its shape.

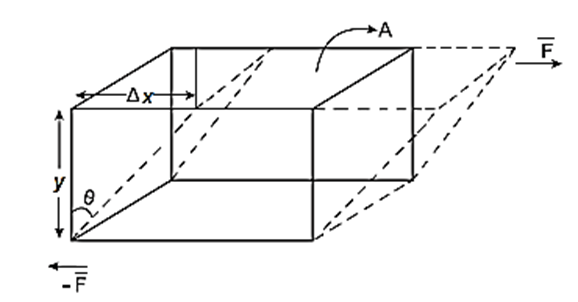
Poisson’s ratio:

Under longitudinal stress (tensile or compressive), longitudinal strain in a body is accompanied with lateral strain. Within elastic limit,

Lateral strain ∝ longitudinal strain

Lateral strain = σ. longitudinal strain

where the constant of proportionality σ is called Poisson's ratio.

Definition : Within the elastic limit, the ratio of lateral strain to the linear strain is called Poisson's ratio.

• Poisson’s ratio is so named in honour of Simeon—Denis Poisson (1781-1840). French mathematician (contributed to mathematical physics).

Explanation :

Let L and D be the original length and diameter of a rod/wire. When it is axially stretched or compressed, let ΔL and ΔD be the changes in its length and diameter, respectively.

∴ Poisson's ratio, σ = \(\frac{lateral\,\,strain}{longitudinal\,\,strain}=\frac{ΔD/D}{ΔL/L}\)

As strain is dimensionless and has no unit, Poisson’s ratio is a pure number i.e., it has no unit.

For a homogeneous isotropic solid, theoretically, −1 < σ < 0.5. For most metals, 0.2 < σ < 0.4.

Lateral strain : When a wire is axially stretched, its diameter decreases. That is, longitudinal extension causes lateral contraction. Conversely, longitudinal compression of a rod causes lateral extension.

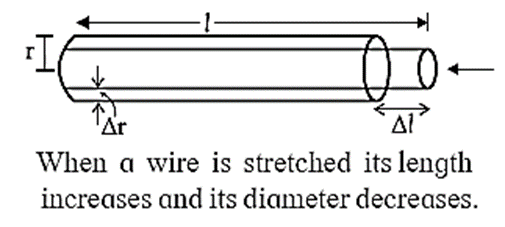
Thus, longitudinal strain is accompanied with lateral strain. Lateral strain is defined as the ratio of the change in diameter to the original diameter of a wire or rod.

Let L and D be the original length and diameter of the wire. When it is axially stretched, let the increase in its length be ΔL and the decrease in its diameter be ΔD.

Longitudinal (tensile) strain = \(\frac{\text{change in length}}{\text{original length}}=\frac{ΔL}{L}\)

Lateral strain = \(\frac{\text{change in diameter}}{\text{original diameter}}=\frac{ΔD}{D}\)

Q. When a wire is stretched, assuming the volume of the wire remaining unchanged, show that Poisson's ratio of the material of wire is 0.5.

Poisson ratio, σ of some familiar materials :

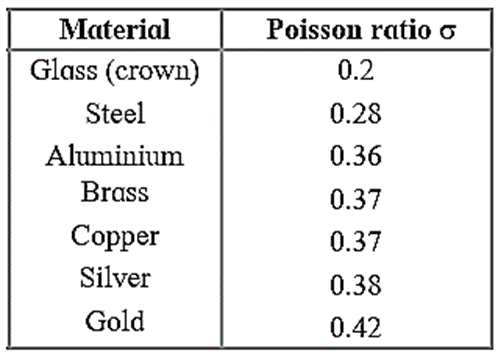
For most of the commonly used metals, the value of σ is between 0.25 and 0.35.

Many times we assume that volume is constant while stretching a wire. However, in reality, its volume also increases. Using approximations it can be shown that σ_max ≈

0.5 if volume is unchanged. In practice, it is much less. This shows that volume also increases while stretching.

Stress-Strain Curve:

Explanation of the behaviour of a metal wire under increasing load : When any stress is plotted against the appropriate strain, the resulting stress-strain graph is found to have different shapes depending on the kind of material. Even among metals there are wide variations.

• The graph (see Fig.) shown is a typical stress-strain graph for a wire of ductile metal.
• The stress is a simple tensile stress and the strain is the percentage elongation.
• During the portion of the curve, up to strain <1%, the stress and strain are proportional until the point a, the proportional limit, is reached.
• The proportional relation between stress and strain in this region is called Hooke’s law.

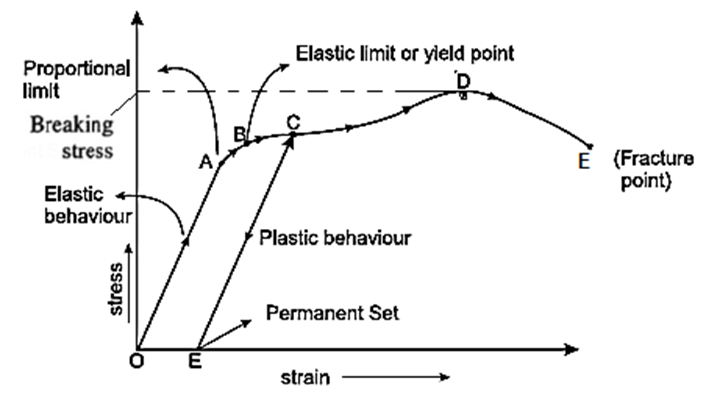
• From A to B stress and strain are not proportional, but, if the load is removed at any point between O and B, the wire is restored to its original length.
• In this region OB, the material is said to be elastic and the point B is called the elastic limit or yield point.
• If the wire is loaded further, the strain increases rapidly, but when the load is suddenly removed at some point beyond B, say at C, the wire does not regain its original length but follows the dashed line.
• The length at zero stress is now greater than the original length and the wire is said to have a permanent set.
• Further increase of load beyond C produces a large increase in strain until a point E is reached at which fracture takes place. From B to E the metal is said to undergo plastic flow or plastic deformation, during which slipping takes place within the metal along the planes of maximum shearing stress.
• Point D indicates the beginning of severe non-uniform plastic deformation as a ‘neck’ begins to form at the weakest portion of the wire.
• The actual area of cross section may be only a fraction of the original cross sectional area so that the true stress at the neck continues to increase until the wire breaks at E (fracture point).
• If large plastic deformation takes place between the elastic limit and the fracture point, the metal is said to be ductile. If fracture occurs soon after the elastic limit, the metal is said to be brittle.

Types of material :

• Brittle :Materials such as glass, ceramics, etc. break within the elastic limit. They are called brittle.
• Ductile : Metals such as copper, aluminum, wrought iron, etc. have large plastic range of extension. They lengthen considerably and undergo plastic deformation till they break. They are called ductile.
• Malleable : Metals such as gold, silver which can be hammered into thin sheets are called malleable

Elastomer : A material which can be elastically stretched to a large value of strain is called an elastomer.

• Rubber has large elastic region. It can be stretched so that its length becomes many times its original length, after removal of the stress it returns to its original state but the stress strain curve is not a straight line.
• Rubber is not perfectly elastic. With each use, a rubber band acquires a permanent increase in its length as a result of increase in intermolecular separation.

Elastic hysteresis : In case of vulcanized rubber, when the stress applied on a body decreases to zero, the strain does not return to zero immediately. The strain lags behind the stress. This lagging of strain behind the stress is called elastic hysteresis.

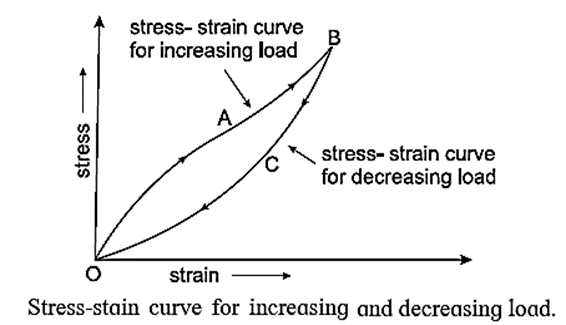
Above figure shows the stress-strain curve for increasing and decreasing load. It encloses a loop. Area of loop gives the energy dissipated during deformation of a material.

Strain Energy:

The elastic potential energy gained by a wire during elongation by a stretching force is called as strain energy.

Hardness:

Hardness : Hardness is the property of a material which enables it to resist plastic deformation.

• Hard materials have little ductility and they are brittle to some extent.
• The term hardness also refers to stiffness or resistance to bending, scratching abrasion or cutting.
• It is the property of a material which gives it the ability to resist permanent deformation when a load is applied to it.
• The greater the hardness, greater is the resistance to deformation.
• Example of the hardest material is diamond. It is incredibly difficult to scratch a diamond. Metal with very low hardness is aluminium. Softest material is plasticine clay

Toughness : The ability of a material to resist fracturing when a force is applied to it is called toughness.

A single material may be hard, strong and tough, e.g.,

• Bulletproof glass is hard and tough but not strong.
• Drill bits must be hard, strong and tough for their work.
• Anvils are very tough and strong but they are not hard.

Friction in Solids:

Friction : The property which resists the relative motion between two surfaces in contact is called friction.

Concept/nature of frictional force :

• Frictional forces are generated along the surfaces of both objects that are in contact when they move or have a tendency to move in relation to one another.
• This force operates on each body in the opposite direction from the direction in which it moves or tends to move.
• The force of static friction resists the attempt to set one body into motion across the surface of another.
• Till the relative motion begins, the force of static friction is self-adjusting, meaning that its magnitude always remains equal to that of the applied force.
• The relative motion begins once the applied force just exceeds this limiting force of static friction.
• Once the relative sliding motion begins, the force of friction that resists the subsequent relative motion is called the force of kinetic friction. This force being less than the limiting force of static friction, a smaller force is required to maintain the motion.

Origin of friction:

Friction between two surfaces of contact arises due to interlocking of the surface irregularities and electromagnetic forces of adhesion between the surfaces. This is true for static friction, kinetic friction, as well as rolling friction.

Consider two clean and smooth metal blocks in contact. Surfaces which are ‘smooth’, in the usual sense of the word, are quite rough at the microscopic level. Even a carefully polished metallic surface has microscopic 'peaks' and ‘valleys'. Hence, when two surfaces are in contact, there is always some interlocking of these surface features.

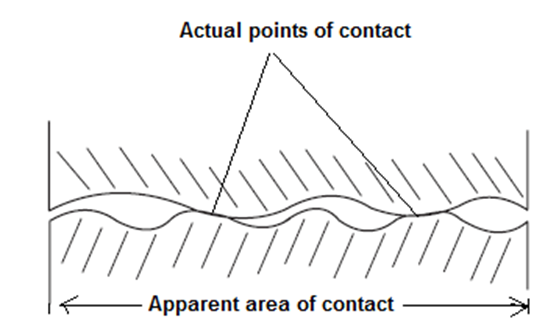
• Major contribution to friction, comes from the adhesive forces between the neutral molecules of the materials in contact.
• Due to the surface irregularities, the bodies touch each other only at few high points of the two surfaces, see above Fig.
• Because molecular attraction decreases rapidly with distance, the adhesion is maximum at these touching high points.
• Also the real or actual area of contact (Ar) at these points is much less than the apparent geometrical area of contact (A).
• It is the area A, which supports the entire normal load. Since Ar << A, the pressure at these microscopic areas of contact is high and strong molecular bonds are formed. To begin relative motion, these bonds must be broken. This is the major source of friction.
• The component of the applied force parallel to the surfaces must have certain minimum non-zero value to be able to break the bonds apart.
• When there is relative motion, there is making and breaking of bonds all the time.

Types of friction:

(i) Static friction: The frictional force which balances applied force when the body is static is called force of static friction, F_s. In other words, static friction prevents sliding motion.

• Up to a certain limit, the force of static friction changes with the applied force such that the two forces are equal in magnitude and opposite in direction, keeping the body at rest. Hence, the force of static friction is known as ’self-adjusting force’.
• Up to a certain limit, the force of static friction increases with the applied force, keeping the body at rest. As the applied force is increased, just before the relative motion begins, the frictional force becomes maximum. It is called the limiting force of friction.

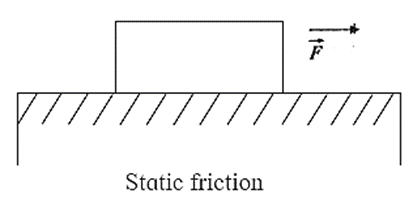
For F = F_max, the object will start moving.

For F < F_max, the force of static friction is equal to F.

For F ≥ F_max, the kinetic friction comes into play.

Laws of static friction :.

• The limiting force of static friction (F_L) is directly proportional to the magnitude of the normal reaction (N) between the two surfaces in contact : F_L ∝ N.
• The limiting force of static friction is independent of the apparent geometrical area between the surfaces in contact, so long as the normal reaction remains the same.
• The limiting force of static friction depends upon materials in contact and the nature of their surfaces.

Coefficient of static friction (μ_S) : The coefficient of static friction is defined as the ratio of the limiting force of friction (F_L) to the normal reaction (N) between the two surfaces in contact : μ_S = F_L/N.

(ii) Kinetic friction : Friction between two surfaces in contact when one body is actually sliding over the other body, is called kinetic friction or dynamic friction.

Laws of kinetic friction :

• The magnitude of the force of kinetic friction (F_k) is directly proportional to the magnitude of the normal reaction (N) between the two surfaces in contact : F_k ∝ N.
• The force of kinetic friction is independent of shape and apparent area of the surfaces in contact.
• The force of kinetic friction depends upon the nature and material of the surfaces in contact.
• The magnitude of the force of kinetic friction is independent of the relative velocity between the object and the surface provided that the relative velocity is neither too large nor too small.

Coefficient of kinetic friction (μ_k) : The coefficient of kinetic friction is defined as the ratio of the force of kinetic friction (F_k) to the normal reaction (N) between the two surfaces in contact. μ_k = F_k/N.

Remember :

• Being a ratio of two similar quantities, the coefficient of friction μ_S and μ_k has no unit and dimensions. It is a pure number.
• The coefficient of friction depends on the normal reaction between the surfaces in contact, the materials and nature of the surfaces.

Rolling friction : Friction between two bodies in contact when one body rolls over the other, is called rolling friction. In this case, the point of contact between the surfaces keeps changing.

• In general, rolling friction < kinetic friction < static friction.
• As rolling friction is the minimum, ball bearings are used to reduce friction in parts of machines to increase its efficiency.

Advantages of friction:

Friction is necessary in our daily life.

• We can walk due to friction between ground and feet.
• We can hold object in hand due to static friction.
• Brakes of vehicles work due to friction; hence we can reduce speed or stop vehicles.
• Climbing on a tree is possible due to friction.

Disadvantages of friction

• Friction opposes motion.
• Friction produces heat in different parts of machines. It also produces noise.
• Automobile engines consume more fuel due to friction.

Methods of reducing friction

• Use of lubricants, oil and grease in different parts of a machine.
• Use of ball bearings converts kinetic friction into rolling friction.
• Giving a body an aerodynamic shape.
• Using antifriction metals.

Q. Explain : lubricant use for reducing friction.

Q. Explain how friction helps us to walk.

Q. Why is it difficult to walk on dry sand?