Thermodynamics
Maharashtra Board-Class-12th-Physics-Chapter-4
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction
Thermodynamics : Thermodynamics is the branch of physics that deals with the concepts of heat and temperature and the inter-conversion of heat and other forms of energy.
Temperature : The temperature of a body is a quantitative measure of the degree of hotness or coolness of the body. According to the kinetic theory of gases, it is a measure of the average kinetic energy per molecule of the gas.
- Temperature difference determines the direction of flow of heat from one body to another or from one part of the body to the other.
- Its SI unit is the kelvin (K).
Heat : When two bodies are in thermal contact with each other, there is a transfer of energy from the body at higher temperature to the body at lower temperature. The energy in transfer is called the heat. Also when two parts of a body are at different temperatures, there is a transfer of energy from the part at higher temperature to the other part.
- The SI unit of heat is the joule.
[Rumford’s experiments showed that caloric did not exist and heat is the motion of the particles of a body. He measured the relation between work done and corresponding heat produced. The result was not accurate, but important in development of thermodynamics.]
Thermal equilibrium
Thermal equilibrium : A system is in a state of thermal equilibrium if there is no transfer of heat (energy) between the various parts of the system or between the system and its surroundings.
- We can say that when two objects are at the same temperature, they are in thermal equilibrium.
- Two systems are said to be in thermal equilibrium when they are in thermodynamic states such that, if they are separated by a diathermic (heat conducting) wall, the combined system would be in thermal equilibrium, i.e., there would be no net transfer of heat (energy) between them.
Zeroth law of thermodynamics
Zeroth law of thermodynamics : If two systems are each in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.
Explanation :
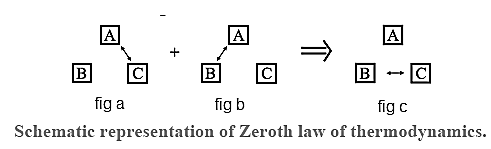
Consider three systems A, B and C. Suppose A and C are in thermal equilibrium [Fig. a], and A and B are also in thermal equilibrium [Fig.b]. Then B and C are also in thermal equilibrium. [Fig.c]. Thus, A, B and C are at the same temperature and A works as a thermometer.
| Note : The Zeroth law of thermodynamics states that systems in thermal equilibrium are at the same temperature. The zeroth law, therefore, enables us to use a thermometer to compare the temperatures of different objects. |
Heat, internal energy and work
Internal energy : Internal energy of a system is defined as the sum of the kinetic energies of the atoms and molecules belonging to the system, and the potential energies associated with the interactions between these constituents (atoms and molecules). Thus, we can say that, the internal energy of a substance is the total energy of all its atoms/molecules.
Note :
- Internal energy does not include the potential energy and kinetic energy of the system as a whole.
- In the case of an ideal gas, internal energy is purely kinetic.
- In the case of real gases, liquids and solids, internal energy is the sum of potential and kinetic energies.
- For an ideal gas, internal energy depends on temperature only.
- In other cases, internal energy depends on temperature, as well as on pressure and volume.
- According to quantum theory internal energy never becomes zero . Even at 0K. particles have energy called zero-point energy.
| Q. Calculate the internal energy of one mole of argon and oxygen?
Answer :
Argon is a monatomic gas. In this case, with three degrees of freedom, the average kinetic energy per molecule = \(\frac 32\) kBT, ( kB =Boltzmann constant and T is the absolute (thermodynamic) temperature of the gas.) Hence, the internal energy of one mole of argon = NA\(\frac 32\)kBT = \(\frac 32\)RT, where NA is the Avogadro number and R = NAkB is the universal gas constant. Oxygen is a diatomic gas. In this case, with five degrees of freedom at moderate temperatures, the internal energy of one mole of oxygen = \(\frac 52\)RT
[collapse]
|
Thermodynamic system : A thermodynamic system is a collection of objects that can form a unit which may have ability to exchange energy with its surroundings. Everything outside the system is called its surroundings or environment. For example, a gas enclosed in a container is a system, the container is the boundary and the atmosphere is the environment. (see Fig.).
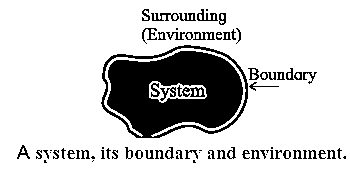
Classification of thermodynamic systems : Depending upon the exchange of energy and matter with the environment, thermodynamic systems are classified as open, closed or isolated.

- A system that can freely exchange energy and matter with its environment is called an open system. Example : water boiling in an open vessel.
- A system that can freely exchange energy but not matter with its environment’ is called a closed system. Example : water boiling in a closed vessel.
- A system that cannot exchange energy as well as matter with its environment is called an isolated system. In practice it is impossible to realize an isolated system as every object at a temperature above 0 K emits energy in the form of radiation, and no object can ever attain 0 K.
- For many practical purposes, a thermos flask containing a liquid can be considered an isolated system.
Thermodynamic process : A thermodynamic process is a process in which the thermodynamic state of a system is changed.
Example : Water contained in a vessel with a lid on it is an open system.
- When the pot is heated externally, water starts boiling after some time and steam is produced which exerts pressure on the walls of the vessel.
- In this case, the state of the water in the container is changed.
- This is because, the temperature (T), the volume (V), and the pressure (P) of the water inside the vessel change when it starts boiling i.e. there is a change in the thermodynamic states of the system.
- Thus, we can describe the state of a system by using temperature, pressure and volume as its variables.
When transfer of energy takes place between a system and its environment, we observe the following conventions.
|
Relation between heat and internal energy :
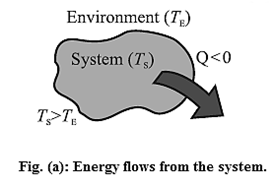
Suppose a system consists of a glass filled with water at temperature TS. Let TE be the temperature of the environment (surroundings) such as the surrounding air in the room. There is a continuous exchange of energy between the system and the surroundings.
If TS > TE, the net effect of energy exchange is the net transfer of internal energy from the system to the environment till thermal equilibrium is reached, i.e., TS and TE became equal. This internal energy in transit is called heat (Q) [Fig (a)]. The change in the temperature of the environment is usually negligible compared with the change in the temperature of the system.
For TS < TE the net effect of energy exchange is the net transfer of internal energy from the environment to the system till TS and TE become equal.
[Fig. (b)] This internal energy in transit is heat (Q).

For TS = TE, there is energy exchange between the system and the environment, but no net transfer of energy. [Fig.(c)]
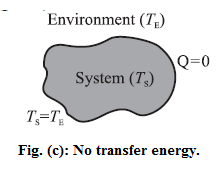
Thus, the net transfer of energy takes place only when there is temperature difference.
Change in Internal Energy of a System :
Consider a system (S) consisting of some quantity of gas enclosed in a cylinder fitted with a movable, massless, and frictionless piston (see below fig.)
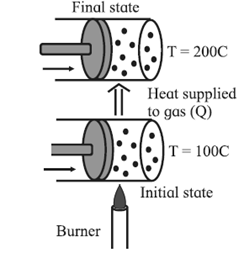
Suppose the gas is heated using a burner (source of heat, environment). Let TS = temperature of the system (gas) and TE = temperature of the environment.
Here, TE > TS. Hence, there will be a net flow of energy (heat) from the environment to the system causing the increase in the internal energy of the system.
The other way to increase the internal energy of the gas is to quickly push the piston inside the cylinder, so that the gas is compressed, as shown in below Fig.
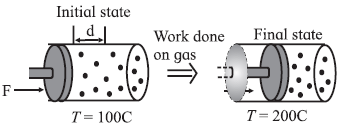
In this case, we know that the piston does some work on the system (gas) in moving it through some distance. The system gains energy and its temperature is increased. On the other hand, if the system (gas) pushes the piston out, so that the gas is expanded, some work is done by the system (gas). It loses some of its energy and the system (gas) cools down.
Q. Why is there a change in the energy of a gas when its volume changes ?
When we compress a gas, we increase the momentum of gas molecules, thereby increasing the energy of the gas. On the contrary, in the expansion of a gas, there is decrease in the momentum of gas molecules resulting in decrease in the energy of the gas.
| During the middle of nineteenth century, James Joule showed that mechanical work done and the heat produced while doing that work are equivalent. This equivalence is the mechanical equivalent of heat. The relation between the mechanical work W and the corresponding heat produced H is W = J × H. The constant J is the mechanical equivalent of heat. |
First law of thermodynamics
First law of thermodynamics : The change in the internal energy of a system (DU) is the difference between the heat supplied to the system (Q) and the work done by the system on its surroundings (W).
Mathematically, ΔU = Q − W, which is the same as Q = ΔU + W.
- if Q is positive, it means heat is added to the system. If Q is negative, it means heat is given out by the system or removed from the system.
- If ΔU is positive, it means there is increase in the internal energy of the system. If ΔU is negative, it means there is decrease in the internal energy of the system.
- If W is positive, it means it is the work done by the system on its surroundings. Negative W means work is done on the system by the surroundings.
- The first law of thermodynamics is largely due to Joule. It is essentially the law of conservation of energy applied to the systems that are not isolated, i.e., the systems that can exchange energy with the surroundings.
(i) Positive work done by a system on the basis of the kinetic theory of gases :
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. See fig.

During expansion of the gas, molecules colliding with the piston lose momentum to it. This exerts force and hence pressure on the piston, moving it outward through a finite distance. Here, the gas does a positive work on the piston. There is increase in the volume of the gas. The work done by the piston on the gas is negative.
(ii) Negative work done by a system on the basis of the kinetic theory of gases :
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. See fig.
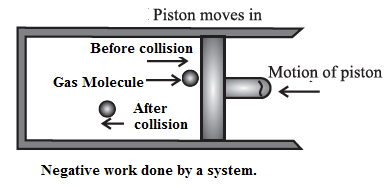
During compression of the gas, molecules colliding with the piston gain momentum from it. The piston moving inward through a finite distance exerts force on the gas. Here, the gas does a negative work on the piston. There is decrease in the volume of the gas. The work done by the piston on the gas is positive.
Expression for the work done by a gas :
Consider a system consisting of some quantity of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. See Fig.
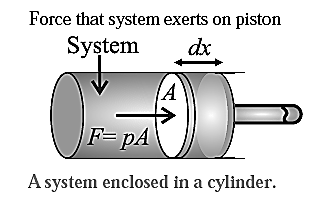
Let the cross sectional area of the cylinder (and the piston) be A, and the constant pressure exerted by the system on the piston be p.
The total force exerted by the system on the piston will be F = pA.
If the piston moves through an infinitesimal (very small) distance dx, the work done by this force is,
dW = pAdx
But Adx = dV, the infinitesimal change in the volume of the cylinder. Hence, the work done by the system in bringing out this infinitesimal change in the volume can be written as,
dW = pdV
If the initial volume of the cylinder is Vi and its volume after some finite change is Vf, then the total work done in changing the volume of the cylinder is,
W = \(\int_{V_f}^{V_i}pdV = p(V_f-V_i)\)
The change in volume in this case is small.
p-V diagram :
Positive work with varying pressure :
Consider some quantity of an ideal gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. See Fig.
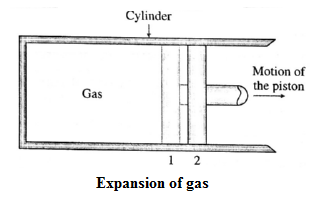
Suppose the gas is allowed to expand by moving the piston outward extremely slowly. There is decrease in pressure of the gas as the volume of the gas increases. Figure shows the corresponding p— V diagram.
In this case, the work done by the gas on its surroundings,
W = \(\int_{V_2}^{V_1}pdV\) (= area under the curve) is positive as the volume of the gas has increased from V1 to V2.
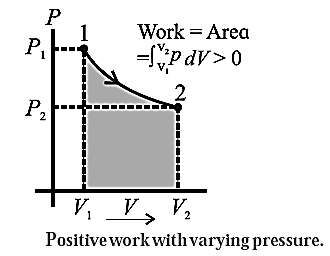
Negative work with varying pressure :
Let us now suppose that starting from the same initial condition, the piston is moved inward extremely slowly so that the gas is compressed.
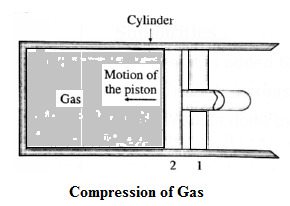
There is increase in pressure of the gas as the volume of the gas decreases.
Below figure shows the corresponding p—V diagram.

In this case, the work done by the gas on its surroundings,
W = \(\int_{V_2}^{V_1}pdV\) ( = area under the curve) is negative as the volume of the gas has decreased from V1 to V2 .
Positive work at constant pressure :
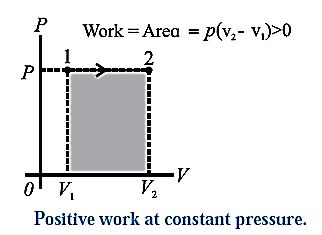
In this case, during the expansion, the work done by the gas,
W = \(\int_{V_2}^{V_1}pdV\) = P(V2—V1) is positive as V2 > V1.
Q. Verify that the area under the P— V curve has dimensions of work
Ans. Area under the P— V curve is , where P is the pressure and V is the volume.
[pressure] = \(\frac{[Force]}{[Area]}=\frac{[MLT^{-2}]}{L^2}\)
[Volume]=[M0L3T0]
[pressure] x [Volume] = \(\frac{[MLT^{-2}]}{L^2}\times [L^3]\)
=[MLT-2][L]= [Force]x[Distance] = [Work]
Thermodynamics state variables
Property of a system or a system variable : The property of a system or a system variable is any measurable or observable characteristic or property of the system when the system remains in equilibrium.
Macroscopic variables of a system : Pressure, volume, temperature, density, mass, specific volume, amount of substance (expressed in mole) are macroscopic variables of a system.
- The quantities specified above are not totally independent, e.g.,
- Density = mass/ volume
- Specific volume = 1 / density.
Intensive variable : A variable that does not depend on the size of the system is called an intensive variable. Examples : pressure, temperature, density.
Extensive variable : A variable that depends on the size of the system is called an extensive variable. Examples : internal energy, mass.
Mechanical equilibrium : A system is said to be in mechanical equilibrium when there are no unbalanced forces within the system and between the system and its surroundings. OR
A system is said to be in mechanical equilibrium when the pressure in the system is the same throughout and does not change with time.
Note : The constituents of a system, atoms, molecules, ions, etc. are never at rest, within a system, even in the condition of equilibrium, statistical fluctuations do occur, but the time of observation is usually very large so that these fluctuations can be ignored
Chemical equilibrium : A system is said to be in chemical equilibrium when there are no chemical reactions going on within the system. OR
A system is said to be in chemical equilibrium when its chemical composition is the same throughout the system and does not change with time.
Note : In this case, in the absence of concentration gradient, there is no diffusion, i.e., there is no transport of matter from one part of the system to the other.
Thermal equilibrium : A system is said to be in thermal equilibrium when its temperature is uniform throughout the system and does not change with time.
- A thermodynamic system is not always in equilibrium. For example, when an inflated ball is punctured, the air inside it suddenly expands to the atmosphere. This is not an equilibrium state. During the rapid expansion, pressure of the air may not be uniform throughout.
- Similarly, the fuel (a mixture of petrol vapour) in the cylinder of an automobile engine undergoing an explosive chemical reaction when ignited by a spark is not an equilibrium state.
- This is because its temperature and pressure are not uniform. Such system which is not in equilibrium cannot be described in terms of the state variables.
Eventually, the air in first case, and the fuel in the second case reach a uniform temperature and pressure and attain thermal and mechanical equilibrium with its surroundings. Thus it attains thermodynamic equilibrium.
Equation of state : The mathematical relation between the state variables (pressure, volume, temperature, amount of the substance) is called the equation of state.
In the usual notation, the equation of state for an ideal gas is PV = nRT.
For a fixed mass of gas, the number of moles, n, is constant. R is the universal gas constant. Thus, out of pressure (P), volume (V) and thermodynamic temperature (T), only two (any two) are independent. It could be p and V, or p and T, or V and T.
Thermodynamics process
Thermodynamic process : A procedure by which the initial state of a system changes to its final state is called a thermodynamic process. During the process, there may be
- addition of heat to the system
- removal of heat from the system
- change in the temperature of the system
- change in the volume of the system (v) change in the pressure of the system.
Quasistatic process : A quasistatic process is an idealised process which occurs infinitely slowly such that at all times the system is infinitesimally close to a state of thermodynamic equilibrium. Although the conditions for such a process can never be rigorously satisfied in practice, any real process which does not involve large accelerations or large temperature gradients is a reasonable approximation to a quasistatic process.
Work Done During a Thermodynamic Process:
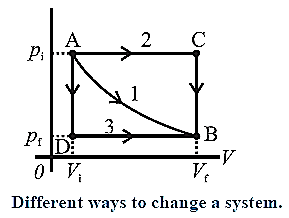
Let us understand the relation between a path and the work done along a path. In the above diagram, the initial state of a gas is characterized by (Pi,Vi) [corrosponding to point A] and the final state of the gas is characterized by (Pf,Vf) [corresponding to point B].
- Path 1 corresponds to constant temperature.
- Path 2 corresponds to the combination AC [P constant] +CB [V constant].
- Path 3 corresponds to the combination AD [V constant] + DB [P constant].
The work done by the gas (W) is the area under the curve and is different in each case.
This shows that the work done by a system depends on the process even when the initial and final states are the same.
According to the first law of thermodynamics in the usual notation,
Q = ΔU + W.
Now, change in internal energy ΔU, depends upon the change in temperature and is fixed once points A and B are fixed because PiVi = nRTi and PfVf = nRTf.W depends on the path followed.
Hence, it follows that heat transferred to the system (Q) depends on the path followed.
Reversible process : A reversible process is one which is performed in such a way that, at the conclusion of the process, both the system and its local surroundings are restored to their initial states, without producing any change in the rest of the universe. A process may take place reversibly if it is quasistatic and there are no dissipative effects. Such a process cannot be realized in practice.
Irreversible process : A process which does not fulfill the rigorous requirements of reversibility is said to be an irreversible process. Thus, in this case, the system and the local surroundings cannot be restored to their initial states without affecting the rest of the universe. All natural processes are irreversible.
Causes of irreversibility :
- Some processes such as a free expansion of a gas or an explosive chemical reaction or burning of a fuel take the system to non-equilibrium states.
- Most processes involve dissipative forces such as friction and viscosity (internal friction in fluids).
- These forces can be minimized, but cannot be eliminated.
Examples of irreversible process :
- When two bodies at different temperatures are brought in thermal contact, they attain the same temperature after some time due to energy exchange. Later, they never attain their initial temperatures.
- Free expansion of a gas.
- A gas seeping through a porous plug.
- Collapse of a soap film after it is pricked.
- All chemical reactions.
- Diffusion of two dissimilar inert gases.
- Solution of a solid in water.
- Osmosis.
Q. Explain, free expansion of gas is irreversible process
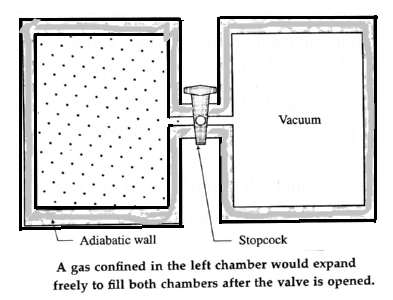
A free expansion is an adiabatic process. i.e., a process in which no heat is added to the system or removed from the system. Consider a gas confined by a valve to one half of a double chamber with adiabatic walls while the other half is evacuated.
When the gas is in thermal equilibrium, the gas is allowed to expand to fill the entire chamber by opening the valve. No interaction takes place and hence there are no local surroundings. While rushing into a vacuum, the gas does not meet any pressure and hence no work is done by the gas. The gas only changes state isothermally from a volume Vi to a larger volume Vf.
To restore the gas to its initial state, it would have to be compressed isothermally to the volume Vi an amount of work W would have to done on the gas by some mechanical device and an equal amount of heat would have to flow out of the gas into a reservoir. If the mechanical device and the reservoir are to be left unchanged, the heat would have to be extracted from the reservoir and converted completely into work. Since this last step is impossible, the process of free expansion is irreversible.
It can be shown that the diffusion of two dissimilar inert gases is equivalent to two independent free expansions. It follows that diffusion is irreversible.
Remember :
|
Isothermal process : A process in which changes in pressure and volume of a system take place at a constant temperature is called an isothermal process.
For such a system ΔT = 0. Isothermal process is a constant temperature process.
Expression for the work done by a gas in an isothermal process.
Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. Let Pi, Vi and T be the initial pressure, volume and absolute temperature respectively of the gas. Consider an isothermal expansion (or compression) of the gas in which Pf, Vf and T are respectively the final pressure, volume and absolute temperature of the gas. Assuming the gas to behave as an ideal gas,
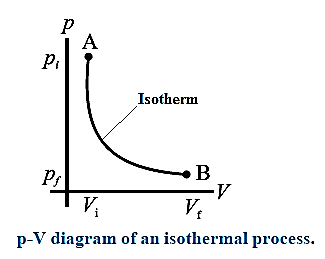
We have, its equation of state :
PV = nRT = constant as T = constant, R is the universal gas constant. The work done by the gas,
W = \(\int_{V_i}^{V_f}pdV\) =\(\int_{V_i}^{V_f}\frac{nRT}{V}dV\) = nRT(ln Vf – ln Vi )
=\(nRTln\frac{V_f}{V_i}\)
| (1) In usual notation W = \(nRTln\frac{V_f}{V_i}\) and Pi Vi = Pf Vf = nRT in an isothermal process.∴ Vf / Vi = Pi / Pf The above expression for W can be written in various forms such as
W = \(nRTln\frac{P_f}{P_i}\) etc. (2) W is positive if Vf > Vi (expansion). W is negative if Vf < Vi (contraction). (3) At constant temperature, change in internal energy, ΔU = 0, ∴ Q = ΔU +W = W. (4) Isothermal process shown in P— V diagram see above Fig.is also called an isotherm. (5) Melting of ice is an isothermal process. |
Remember for an isothermal process:
- Equation of state: pV = constant
- ΔT = 0. Constant temperature process, perfect thermal equilibrium with environment.
- ΔU = 0. No change in internal energy, energy is exchanged with the environment.
- Q = W. Energy exchanged is used to do work.
- W = p ΔV
- An isothermal change is a very slow change. The system exchanges heat with its environment and is in thermal equilibrium with it throughout the change.
- For an isothermal process, none of the quantities Q and W is zero.
- For an isothermal change, total amount of heat of the system does not remain constant.
Isobaric process : A process in which pressure remains constant is called an isobaric process.
Below figure shows the p-V diagram of an isobaric process. It is called as an isobar. The different curves shown on the maps provided by the meteorology department are isobars. They indicate the locations having same pressure in a region. For an isobaric process, none of the quantities ΔU, Q and W is zero.
Expressions for the work done, change in internal energy and heat supplied in an isobaric process in the case of a gas :
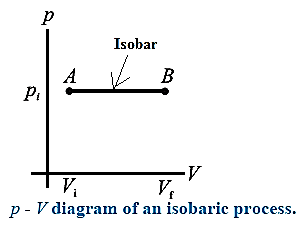
Consider n moles of a gas enclosed in a cylinder fitted with a movable, massless and frictionless piston. We assume that the gas behaves as an ideal gas so that we can use the equation of state pV = nRT.
Consider an isobaric expansion (or compression) of the gas in which the volume of the gas changes from Vi to Vf and the temperature of the gas changes from Ti to Tf when the pressure (p) of the gas is kept constant. The work done by the gas,
W = = p(Vf - Vi ) …..(1)
Now, pVi = nRTi and pVf = nRTf
pVf - pVi = nRTf - nRTi
p(Vf - Vi) = nR(Tf - Ti)
from Eq. (1), W= nR(Tf -Ti) …… (2)
The change in the internal energy of the gas,
ΔU =nCv(Tf -Ti) …… (3)
where Cv is the molar specific heat of the gas at constant volume.
From Eqs. (2) and (3), we have, the heat supplied to the gas,
Q = ΔU + W = nCv(Tf - Ti) + nR(Tf - Ti)
= n(Cv + R)(Tf - Ti)
Q= nCp(Tf - Ti) …..(4)
Where Cp (= Cv +R) is the molar specific heat of the gas at constant pressure.
Remember for an isobaric process:
|
Isochoric process : A process that takes place at constant volume is called an isochoric process (or isometric process).
- It is a constant volume process. A system does no work on its environment during an isochoric change.
- For an isochoric process, ΔV =0, and we have, from the first law of thermodynamics, ΔU = Q.
- This means that for an isochoric change, all the energy added in the form of heat remains in the system itself and causes an increase in its internal energy. Heating a gas in a constant volume container or diffusion of a gas in a closed chamber are some examples of isochoric process.
Expressions for the work done, change in internal energy and heat supplied in isochoric process :

As there is no change in volume in this case, the work done (W) by the system on its environment is zero. The change in the internal energy.
ΔU = nCp(Tf— Ti) and heat supplied, Q= ΔU = nCp(Tf— Ti)
| Remember for an isochoric process:
1. ΔV = 0. Constant volume process. 2. W = 0. No work is done because volume remains constant, ΔV = 0. 3. Q = ΔU. Energy exchanged is used to change internal energy. 4. ΔT ≠ 0. Temperature of the system changes. |
Adiabatic process : A process during which there is no transfer of heat (energy) from the system to the surroundings or from the surroundings to the system is called an adiabatic process.
For an adiabatic change, Q = 0. Heat transfer to or from the system is prevented by either perfectly insulating the system from its environment, or by carrying out the change rapidly so that there is no time for any exchange of heat.
Examples : Puncturing an inflated balloon or a tyre.
Expressions for the work done by a system (an ideal gas) in an adiabatic process :
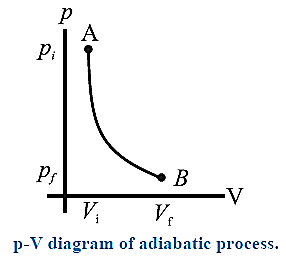
It can be shown that if an ideal gas is subjected to an adiabatic process, then,
PVγ = constant = C, where γ = Cp/Cv. γ is called the adiabatic ratio. Cp is the molar specific heat of the gas at constant pressure and Cv is the molar specific heat at constant volume.
Let Pi = initial pressure, Pf final pressure, Vi = initial volume and Vf = final volume of the gas taken through an adiabatic process.
The work done by the gas,
W = \(\int_{V_i}^{V_f}pdV = \int_{V_i}^{V_f}\frac{C}{V^\gamma }dV\)
= \(\int_{V_i}^{V_f}V^{-\gamma}dV = c(\frac{V^{-\gamma +1 }}{-\gamma+1 })^{V_f}_{V_i}\)
= \(\frac{C}{1-\gamma }(V_{f}^{-\gamma +1}-V_{i}^{-\gamma +1})\)
Now C =PiViγ = PfVfγ
∴ W = \(\frac{1}{1-\gamma }(P_fV_f^\gamma V_{f}^{-\gamma +1}-P_iV_i^\gamma V_{i}^{-\gamma +1})\)
= \(\frac{P_fV_f-P_iV_i}{1-\gamma } = \frac{P_iV_i-P_fV_f}{\gamma -1 }\)
Now, PiVi=nRTi and PfVf= nRTf, where n is the number of moles of the gas, Ti is the initial temperature of the gas, Tf is the final temperature of the gas and R is the universal gas constant.
∴ W = \(\frac{nRT_i-nRT_f}{\gamma -1 } = \frac{nR(T_i-T_f)}{\gamma -1 }\)
= \(\frac{nR(T_i-T_f)}{\frac{C_P}{C_V}-1 }=\frac{nR(T_i-T_f)}{(\frac{C_P-C_V}{C_V})}\)
= nCv(Ti-Tf) ….. as Cp - Cv = R
| Note : We have Q = ΔU + W = 0 in an adiabatic process.
W = — ΔU = —nCv(Tf—Ti) = nCV(Ti—Tf) |
Q. Explain the term free expansion of a gas.
When a balloon is ruptured suddenly, or a tyre is punctured suddenly, the air inside the balloon/ tyre rushes out rapidly to the atmosphere.
Always remember for an adiabatic process:
|
Q. Why is the P-V curve for an adiabatic process steeper than that for an isothermal process ?
Adiabatic process : PVγ = constant VγdP + gPVγ-1dV = 0 \ dP/dV= γP/V Isothermal process : PV = constant ∴ PdV + VdP = 0 ∴ dP/dV= P/-V Now γ > 1 ∴ dP/dV (adiabatic) > \ dP/dV (isotherm) dP/dV is the slope of the P—V curve. ∴ The P—V curve for an adiabatic process is steeper than that for an isothermal process.
Cyclic Process:
A thermodynamic process that returns a system to its initial state is a cyclic process.
In this process, the initial and the final state is the same. Below figure shows the p-V diagram of a cyclic process.
Path 1 shows how the state of the system (ideal gas) is changed from (Pi, Vi) [point A] to (Pf, Vf) [point B]. Path 2 shows the return of the system from point B to point A.
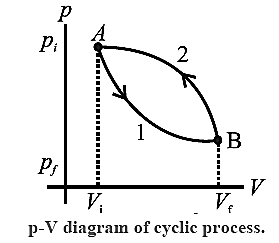
As the system returns to its initial state, the total change in its internal energy is zero. (ΔU = 0).
According to the first law of thermodynamics, Q = ΔU + W we have, for a cyclic process, Q = 0+ W = W
The area enclosed by the cycle in P— V plane gives the work done (W) by the system.
Remember : Working of a heat engine is a cyclic process.
Download PDF from store : Chapter-4-Thermodynamics-Text Book Get PDF from store : Chapter-4-Thermodynamics-Notes Get PDF from store : Chapter-4-Thermodynamics-Solution
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-3-Kinetic Theory of Gases and Radiations –Online Notes Next Chapter :Chapter-5-Oscillations – Online Notes
it was helpful
It is very useful
Great job