Notes-Part-1-Class-11-Science-Physics-Chapter-7-Thermal Properties of Matter-Maharashtra Board

Topics to be Learn : Part-1 Introduction Temperature and Heat Measurement of temperature Absolute temperature and ideal gas equation Thermal expansion Topics to be Learn : Part-2 Specific heat capacity Calorimetry Change of state Heat transfer Newton's law of cooling

Introduction :

• The sensation of hot or cold is a matter of daily experience.
• When we say a body or water is hot, we actually mean that its temperature is more than our hand. However, in this way, we can only compare the hotness or coldness of two objects qualitatively.
• Hot and cold are relative terms.
• Lukewarm water seems colder than hot water but hotter than cold water to our hands. A hand immersed in hot water for some time finds lukewarm water cooler, whereas a hand immersed in cold water for some time finds the same lukewarm water hot. Thus, the sense of touch cannot be relied upon to judge the temperature of a substance.
• We ascribe a property ‘temperature’ to an object to determine its degree of hotness.
• The higher the temperature, the hotter is the body.

Temperature and Heat:

Temperature :

• The temperature of a body is a quantitative measure of the degree of hotness or coolness of the body.
• It is a measure of the average kinetic energy per particle of the body.
• It determines the direction of heat flow from one body to another or from one part of the body to the other.
• Temperature is one of the physical quantities used to define the thermodynamic state of a system.
• The SI unit of temperature is the kelvin.
• The dimension of temperature is [L⁰M⁰T⁰K¹].

Heat :

When two bodies come into thermal contact with each other, energy is exchanged between them. This leads in a net flow of energy from the higher-temperature body to the lower-temperature body. The energy transferred is known to as heat.

• Heat is the energy transferred between two bodies, or between two parts of the same body, or, in general, between a body and its surroundings, by virtue of temperature difference.
• The direction of heat flow is from a region at higher temperature to that at lower temperature.
• Temperature is the fundamental quantity required to study the properties or phenomena related to heat in addition to length, mass and time.

Unit of Heat :

• In the CGS system, heat, being energy, is expressed in erg (called mechanical unit) as well as calorie (called heat unit).
• The SI unit of heat is the joule (J).
• The dimension of temperature is [L⁰M⁰T⁰K¹]
• The dimensions of heat are [L²M¹T²K⁰].

One Erg : One erg is the work done when a force of one dyne displaces a body through 1 cm in the direction of the force. One erg = 1 dyn.cm. One calorie : It is the amount of heat that must be transferred to 1 g of water to raise its temperature through 1 °C from 14.5 °C to 15.5 °c. 1 calorie = 4.186 x 107 ergs. One joule : It is the work done when the point of application of a force of one newton moves a distance of one metre in the direction of the force. 1 joule = 107 ergs. 1 calorie (cal) = 4.186 joules (J), 1 J = 0.2395 cal.

Thermal equilibrium :

If there is no net heat transmission between the various components of the system or between the system and its surroundings, the system is said to be in a state of thermal equilibrium.

Thermal or internal energy :

• At any particular temperature, a body's atoms or molecules are perpetually in motion. While they mostly move translationally in liquids and gases, they oscillate around their mean positions in solids. Hence, they possess kinetic energy.
• Besides, atoms or molecules in solids and liquids are closely packed due to strong interatomic and intermolecular attractive forces. Due to these forces they also possess potential energy. This is, however, negligible in gases because of the relatively large intermolecular separations.
• The sum of the kinetic and potential energies of all the constituent particles of a body is called the thermal or internal energy of the body.
• When a body receives energy in the form of heat, its thermal energy increases and its particles move faster.

Remember : Heat supplied to the substance increases the kinetic energy of molecules or atoms of the substance. The average kinetic energy per particle of a substance defines the temperature.

Solid have a definite shape but a liquid made from the same substance does not have a definite shape :

Reason :

• In the solid state of a substance, its individual particles have fixed mean positions with respect to each other. Due to thermal energy, the particles vibrate about their mean positions. But the thermal energy is not enough to overcome the intermolecular attraction. As a result, a solid has a definite shape.
• On heating, thermal energy overcomes intermolecular attraction, thus the bonds weaken. The particles move about each other while remaining in contact. This corresponds to the liquid state. In this state, the particles still remain in contact, so a liquid has a definite volume. But because the particles no longer have fixed mean positions, a liquid has no definite shape.

Gases neither have a definite volume nor shape :

Reason : As per kinetic theory of gases, for an ideal gas, there are no forces between the molecules of a gas. Hence gases neither have a definite volume nor shape.

Measurement of Temperature:

Adiabatic wall :

• An adiabatic wall is a wall or partition separating two systems, or a system and its surroundings, that does not allow any exchange of heat between them. Thus, an adiabatic wall is a perfect thermal insulator,
• g., partitions made from the materials such as plastic, glass wool, wood, etc.
• The systems separated by an adiabatic wall are said to be thermally isolated.
• An adiabatic wall is generally shown with slanting lines or as a thick cross-shaded region

Diathermic wall :

• A diathermic wall is a wall or partition between two systems, or a system and its surroundings, that allows exchange of heat between them.
• Example: A partition made of a thin sheet of copper.
• The diathermic wall is represented as a thin dark region.

Know This : Zeroth law of thermodynamics : If three systems are such that, A and B are in thermal equilibrium and also B and C are in thermal equilibrium, then A and C are also in thermal equilibrium. If TA = TB and TB = TC, then TA = TC

 Thermometry :

• Thermometry is the branch of physics concerned with the measurement of temperature and the design and use of a thermometer.
• Any property of matter which changes in a definite way with change in temperature can be used to measure temperature. The said property is called the thermometric property and the corresponding material is called the thermometric material.

Fixed points in thermometry :

• The fact that substances change state from solid to liquid to gas at fixed temperatures is used to define reference temperature called fixed point.
• In thermometry, fixed points are the temperatures that can be measured and reproduced very precisely and fairly easily.
• A fixed point is associated with the physical phenomenon of change of state (melting or boiling) of a pure substance at normal atmospheric pressure.
• Some such fixed points are used to define temperature scales and to calibrate a secondary thermometer.
• The two fixed temperatures selected for this purpose are the melting point of ice or freezing point of water and the boiling point of water.

Ice point : The temperature at which pure water freezes, or ice melts, at standard atmospheric pressure is called the ice point. It is also called the freezing point of water or melting point of ice.

Steam point: The temperature at which pure water boils at standard atmospheric pressure is called the steam point. It is also called the boiling point of water.

Different scales of temperature :

• There are three different scales of temperature namely the Celsius scale, Fahrenheit scale and absolute or thermodynamic scale.
• The units of temperature in these scales are the degree Celsius (°C), degree Fahrenheit (°F) and kelvin (K).

To measure temperature quantitatively, generally two different scales of temperature, Celsius scale and Fahrenheit scale are used. They are describe below.

Celsius scale:-

• On this scale, the ice point is marked as 0 and the steam point is marked as 100, both taken at normal atmospheric pressure (10⁵ Pa or N/m²).
• The interval between these points is divided into 100 equal parts. Each of these is known as degree Celsius and is written as ºC.
• This temperature scale is a revised version of the Centigrade scale, first proposed in 1742 by Anders Celsius (1701-44), Swedish astronomer.

Fahrenheit scale :-

• On this scale, the ice point is market as 32 and the steam point is marked as 212, both taken at normal atmospheric pressure.
• The interval between these points is divided into 180 equal parts. Each division is known as degree Fahrenheit and is written as °
• This temperature scale was invented in 1714 together with the first mercury-in-glass thermometer by Gabriel Daniel Fahrenheit (1686-1736), German physicist.

The relation between these three scales of temperature is

\(\frac{T_C}{100}=\frac{T_F-32}{180} =\frac{T_K-273.15}{100}\)  OR  \(\frac{T_C}{5}=\frac{T_F-32}{9} =\frac{T_K-273.15}{5}\)

where T_C, T_F and T_K are the temperatures in the Celsius scale, Fahrenheit scale and absolute scale, respectively.

Characteristics of an ideal thermometer :

• An important characteristic of a thermometer is its sensitivity, i.e., a thermometer should be able to sense a change in the thermometric property for a very small change in temperature of a body.
• Also, accuracy and reproducibility are the other two characteristics of an ideal thermometer.

Absolute Temperature and Ideal Gas Equation:

Absolute scale of temperature :

The absolute or thermodynamic scale of temperature was proposed in 1848 by Lord Kelvin (William Thomson, 1824-1907, British physicist and electrical engineer).

He suggested the establishment of an absolute thermometric scale which is independent of the properties of any arbitrary kind of matter, as opposed to the

Fahrenheit and Celsius scales on which the zero and each division are arbitrarily defined.

The variation of pressure at constant volume, or that of volume at constant pressure, with temperature provides a very important concept of the lower limit of temperature in the universe and of the absolute scale of temperature.

According to Charles’ law, the volume of a fixed mass of gas at t°C, under a constant pressure is

V = V₀ \((1 +\frac{t}{273.15})\)  …(1)

where V₀ is the volume at 0 °C. Also, from Charles’ law of pressure, the pressure of a fixed mass of gas at t °C, at a constant volume, is

p = p₀ \((1 +\frac{t}{273.15})\)    …(2)

where p₀ is the pressure at 0 °C. Both Eqs. (1) and (2) point to a temperature of — 273.15 °C when the volume or pressure of the gas will reduce to zero, see below Fig.

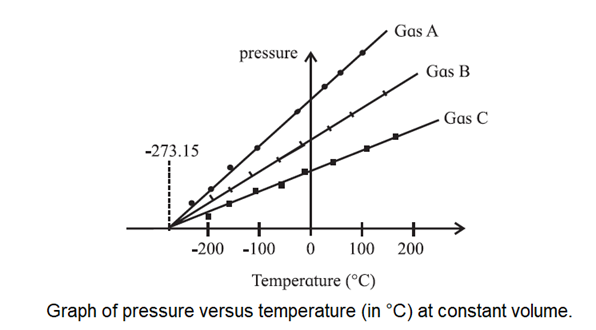
If we use constant-volume gas thermometers filled with gases of different kinds or at different pressures, we will still measure the same temperature. That is why a constant-volume gas thermometer is useful. And, an extrapolation of each of their graphs to zero pressure occurs at the same temperature, — 273.15 °C.

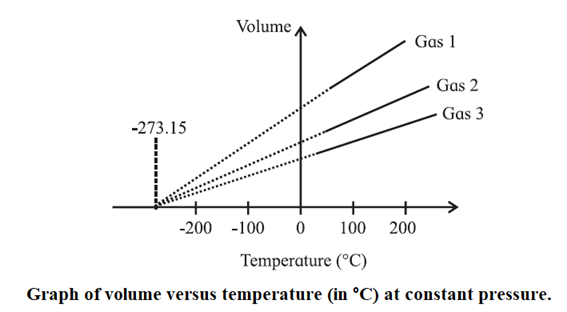
Theoretically, therefore, it is the lowest attainable temperature — the temperature at which every material in the universe will have the least energy and molecular activity. This is taken to be the zero of the absolute scale of temperature and called as the absolute zero of temperature.

Absolute or thermodynamic temperature is indicated by the symbol T, and has the unit kelvin, symbol K. The unit of thermodynamic temperature is defined to be the fraction 1/273.16 of the thermodynamic temperature of the triple point of water. Celsius temperature t is defined by the equation

t (in °C) = T (in K) −273.15

The magnitude of the degree Celsius the unit of Celsius temperature, is defined to be the same as that of the kelvin, 1 °C = 1 K.

Absolute zero of temperature : The absolute zero of temperature, or the zero

of the absolute or thermodynamic scale of temperature, is that temperature at which the energy of atoms and molecules of every material is minimum.

Since t (in °C) = T (in K) − 273.15,

For T = 0 K is

t = 0 − 273.15 = — 273.15 °C

Also, in degree Fahrenheit,

t − 32 =  \(\frac{9}{5}\)(T − 273.15)

= \(\frac{9}{5}\)(0 − 273.15) = − 491.67 °F

∴ t = − 491.67 + 32 = − 459.67 °F

Constant-volume gas thermometer :

• A constant-volume gas thermometer consists of a large glass bulb (of volume about 700 cm³), filled with a pure gas (preferably hydrogen or helium) at low pressure, and connected to a mercury manometer whose open tube is movable.
• The glass bulb is kept at different fixed point temperatures and the volume of the gas is kept constant by adjusting the open tube of the manometer.
• The gauge pressure is noted from the manometer, and hence the absolute pressure p.
• For a given mass, or number of moles, of a gas, we get from the ideal gas equation, pV ∝ T, where V is the volume and T the absolute temperature.
• Hence, for constant V, p ∝ T which is called Charles’ law of pressure (modern form). It is also called Gay-Lussac's law. Thus, the thermometric property used in a constant volume gas thermometer is the pressure of a given mass of gas at constant volume.
• By international agreement, this is one of the four standard thermometric properties.

Boyle's law : The pressure of a fixed mass of gas at constant temperature is inversely proportional to its volume.

If p is the pressure of a fixed mass of gas at a certain temperature and V is the corresponding volume, then,

p ∝ 1/V or pV = constant

when the mass of the gas and its temperature are constant.

Charles’ law : The volume of a fixed mass of gas at constant pressure is directly proportional to its absolute temperature.

Thus, V ∝ T

 ∴ V/T = constant

Ideal gas : An ideal gas is defined to be a gas which obeys all the gas laws at all pressures and temperatures.

A real gas obeys the gas laws, i.e., it can be treated as an ideal gas, only at low

pressures or densities and high temperatures, well above the boiling point of the corresponding liquid.

Equation of ideal gas :

Let p, V and T be the pressure, volume and absolute temperature of n moles of a gas. By the gas laws,

• when p and T are constant, V ∝ n,
• when n and T are constant, V ∝ 1/p,
• when n and p are constant, V ∝

∴ V ∝ \(\frac{nT}{p}\)  ∴ V = R\(\frac{nT}{p}\)

where R is a proportionality constant, called the universal gas constant.

 ∴ pV = nRT

This is the equation of state for an ideal gas or ideal gas equation. It describes the macroscopic behaviour of an ideal gas under all possible conditions.

In SI units, R = 8.314 J/mol.K

Ideal gas equation in terms of the density of the gas :

In the usual notation, pV= nRT and n = m/M ,

where m is the mass of n moles of the gas and M is its molar mass.

∴ pV = \(\frac{m}{M}\)RT

Since density, ρ = \(\frac{m}{V}\)  , p = \(\frac{ρ}{M}\) RT is the required equation.

Ideal gas equation in terms of the Boltzmann constant :

In the usual notation, pV = nRT and n = N/N_A

∴ pV = \(\frac{N}{N_A}\)RT = N\((\frac{R}{N_A})\)T = Nk_BT

Where k_B = \(\frac{R}{N_A}\) is the Boltzmann constant

Importance of a gas thermometer :

Measures of temperature that are defined to be consistent with the laws of thermodynamics are said to be thermodynamic temperatures.

A gas thermometer, constant-volume or constant-pressure, is based on the variation of pressure or volume with thermodynamic or absolute temperature, and by measuring the property, we can calculate temperature directly without any calibration.

Advantages of gas thermometer :

• The coefficient of expansion of a gas is very large, and the thermal capacity very low, in comparison to those of liquids.
• A gas thermometer is more sensitive than liquid-in-glass thermometers, i.e., small changes in temperature can be recorded more accurately. This is because the expansion of the container bulb is negligible, and can be ignored, in comparison with that of the gas, again because the coefficient of expansion of a gas is very large.
• At low densities, i.e., pressures, all gases behave identical to an ideal gas and, therefore, give consistent measures of thermodynamic temperatures.
• A gas thermometer can be used to measure very high as well as very low temperatures (above 5 K).

Thermocouple :

• Thermocouple is an instrument used to measure temperature.
• Two different metals or alloys e.g. copper and iron are joined together to form a junction. These two junctions at the two ends of two dissimilar metal rods are kept at two different temperatures.
• When these junctions experience a temperature difference, an emf is produced. The magnitude of this thermally-generated emf (thermo-emf) for given temperatures of the two junctions is different for different combinations of the metals.
• The relation between thermo-emf and temperature is used for measuring the temperature.

Thermal Expansion:

A change in the temperature of a body causes change in its dimensions. The increase in the dimensions of a body due to an increase in its temperature is called thermal expansion.

There are three types of thermal expansion: (i) Linear expansion, (ii) Areal expansion, (iii) Volume expansion.

(i) Linear expansion :

The expansion in length due to thermal energy is called linear expansion.

The linear thermal expansion of a rod/wire depends upon (i) its material (ii) its original length (iii) the rise in its temperature.

Consider a rod of length L at a certain temperature. If the rod thermally expands by

an amount AL when its temperature rises by ΔT, then ‘

ΔL ∝ L and ΔL ∝ ΔT

∴ ΔL  ∝ L ΔT

∴ ΔL = α L ΔT

where α is the coefficient of linear expansion, which depends only upon the nature of the solid.

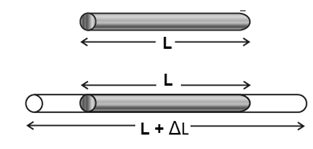
The above equation can be rewritten as

α = \(\frac{ΔL}{L}×\frac{1}{ΔT}\)

where, \(\frac{ΔL}{L}\) is the fractional or relative increase in length.

Definition of coefficient of linear expansion: The coefficient of linear expansion or a linear expansivity, of a solid is the increase in the length of the solid per unit original length at 0 °C per degree Celsius rise in temperature.

(ii) Areal expansion :

The increase ΔA, in the surface area, on heating is called areal expansion or superficial expansion.

The superficial thermal expansion of a solid surface depends upon (i) its material (ii) the original surface area (iii) the rise in its temperature of the solid.

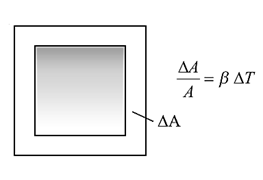
Consider a solid surface of area A at a certain temperature.

If the thermal increase in its surface area is ΔA when its temperature rises by ΔT, then

ΔA ∝ A and ΔA ∝ ΔT

∴ ΔA  ∝ A ΔT

∴ ΔA = β A ΔT

where β is the coefficient of areal or superficial expansion, which depends only upon the material.

The above equation can be written as

 β = \(\frac{ΔA}{A}×\frac{1}{ΔT}\)

where \(\frac{ΔA}{A}\) is the relative increase in surface area. OR

The coefficient of superficial or areal expansion, or areal expansivity, of a solid is defined as the increase in the surface area of the solid per unit original area at 0 °C per degree Celsius rise in temperature.

(iii) Volume expansion :

The increase in volume due to heating is called volume expansion or cubical expansion.

The cubical thermal expansion of a solid surface depends upon (i) its material (ii) its original volume (iii) the rise in its temperature.

Consider a solid of volume V at a certain temperature. If its volume increases by ΔV due to a rise in temperature ΔT, then

ΔV ∝ V and ΔV ∝ ΔT

∴ ΔV  ∝ V ΔT

∴ ΔV = γ V ΔT

where γ is the coefficient of cubical or volume expansion, which depends only upon the nature of the solid.

The above equation can be rewritten as

γ = \(\frac{ΔV}{V}×\frac{1}{ΔT}\)

where \(\frac{ΔV}{V}\) is the relative increase in volume.

Definition : The coefficient of cubical or volume expansion, or volume expansivity, of a solid is defined as the increase in the volume of the solid per unit original volume at 0 °C per degree Celsius rise in temperature.

Relation between the coefficients of linear and areal expansion of a solid :

Consider a square lamina (thin plate) of side L₀ at a temperature T₀. The area of each surface of the lamina at that temperature is A₀ = L₀².

On heating it to a temperature T, each side increases to L_T and the area of each surface to A_T, such that,

L_T = L₀ [1 + α(T − T₀)]    ….. (1)

and A_T = A₀ [1 + β(T − T₀)]     …..(2)

Where α and β are respectively the linear and areal expansion coefficients of the solid.

Also, A_T = L_T² = L₀² [1 + α(T − T₀)]²  

∴ A_T = A₀ [1 + 2α(T − T₀) + α² (T − T₀)²]

Because on is very small (of the order of 10⁻⁵ K⁻¹ to 10⁻⁶ K⁻¹), the term in α² is very

small in comparison to the first two terms in the brackets and may be ignored.

∴ A_T = A₀ [1 + 2α(T − T₀)]          …...(3)

Comparing Eqs. (2) and (3),

β = 2 α         ….(4)

Relation between the coefficients of linear and cubical expansion of a solid :

Consider a cube of side L₀ at a temperature T₀. Its volume at that temperature is

V₀ = L₀³.

On heating it to a temperature T, each side increases to L_T and the volume to V_T, such that,

L_T = L₀ [1 + α(T − T₀)]    ….. (1)

and V_T = V₀ [1 + γ (T − T₀)]    ….(2)

where α and γ are respectively the linear and cubical expansion coefficients of the solid.

Also, V_T = L_T³ = L₀³ [1 + α(T − T₀)]³  

 ∴ V_T = V₀ [1 + 3α(T − T₀)+ 3 α²(T − T₀)² + α³(T − T₀)³]

Because on is very small (of the order of 10⁻⁵ K⁻¹ to 10⁻⁶ K⁻¹), the terms in α² and α³ are very small in comparison to the first two terms in the brackets and may be ignored.

 ∴ V_T = V₀ [1 + 3α(T − T₀)]    …..(3)

Comparing Eqs. (2) and (3),

γ = 3 α    ….(4)

This is the relation between the coefficients of linear and cubical expansion of a solid

Relation between α, β and γ :

We have β = 2α  and γ = 3α    …[From above relations of eq(4)],

∴ 3β = 6α  ……(1)

and 2γ = 6α    ……(2)

Combining Eqs. (1) and (2), we get,

6α = 3β = 2γ

Also, β = 2α  and β = 2α 

Hence, the relation between α, β and γ is α = β/2 = γ/3

Thus, the three coefficients are in the ratio α : β : γ = 1 : 2 : 3

Application of thermal expansion :

• Rails of a railway track thermally expand in summer as well as when a train passes on them at a high speed. If there is no space between consecutive rails for them to expand, they get distorted during expansion, which is potentially disastrous. Hence, consecutive rails are always joined with a small gap between them. Such joints are called thermal expansion joints.
• Bridge spans are also provided with such joints, allowing them to freely expand in summer.
• In factories too, all long pipelines exposed to the elements, as also those carrying hot liquids and gases, are provided with thermal expansion joints.

Anomalous expansion of water :

Liquids, in general, expand when they are heated and contract when cooled. Water exhibits this behaviour at standard pressure between 4 °C and 100 °C. Below 4 °C, instead of contraction, water expands with fall in temperature till 0 °C when it freezes into ice. This phenomenon is called the anomalous expansion of water.

Thus, the volume of a given mass of water is the least at 4 °C, and hence its density is maximum at this temperature.

Know This : When pressure is held constant, due to change in temperature, the volume of a liquid or solid changes very little in comparison to the volume of a gas. The coefficient of volume expansion, γ, is generally an order of magnitude larger for liquids than for solids. Metals have high values for the coefficient for linear expansion, α, than non-metals. γ changes more with temperature than α and β. We know that water expands on freezing from 4 ºC to 0 ºC. Other two substances, that expand on freezing are metals bismuth (Bi) and antimony (Sb). Thus the density of liquid is more than corresponding solid and hence solid Bi or Sb float on their liquids like ice floats on water.