Solutions-Class-10-Mathematics-2-Chapter-5-Coordinate Geometry-Maharashtra Board

Suppose the coordinates of point A are (x₁, y₁) and of point B are (x₂, y₂).

x₁ = 2, y₁ = 3, x₂ = 4 and y₂ = 1

By distance formula,

AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{(4-2)^2+(1-3)^2}$

= $\sqrt{(2)^2+(-2)^2}$

= $\sqrt{4 + 4}$

= $\sqrt{8}$ = $\sqrt{4×2}$ = $2\sqrt{2}$

Answer is : Distance between points A and B is $2\sqrt{2}$ .

Suppose the coordinates of point P are (x₁, y₁) and of point Q are (x₂, y₂).

x₁ = −5, y₁ = 7, x₂ = −1 and y₂ = 3

By distance formula,

PQ = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{[-1-(-5)]^2+(3-7)^2}$

= $\sqrt{(4)^2+(-4)^2}$

= $\sqrt{16 + 16}$

= $\sqrt{32}$

= $\sqrt{16×2}$

= $4\sqrt{2}$

Answer is : Distance between points P and Q is $4\sqrt{2}$ .

Suppose the coordinates of point R are (x₁, y₁) and of point S are (x₂, y₂).

x₁ = 0, y₁ = −3, x₂ = 0 and y₂ = $\frac{5}{2}$

By distance formula,

PQ = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{(0-0)^2+[\frac{5}{2}-(-3)]^2}$

= $\sqrt{(o)^2+(\frac{5}{2}+3)^2}$

= $\sqrt{0+(\frac{5+6}{2})^2}$

= $\sqrt{(\frac{11}{2})^2}$

= $\frac{11}{2}$

Answer is : Distance between points P and Q is $\frac{11}{2}$ .

Suppose the coordinates of point L are (x₁, y₁) and of point M are (x₂, y₂).

x₁ = 5, y₁ = −8, x₂ = −7 and y₂ = −3

By distance formula,

PQ = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{(-7-5)^2+[-3-(-8)]^2}$

= $\sqrt{(-12)^2+(5)^2}$

= $\sqrt{144 + 25}$

= $\sqrt{169}$

= 13

Answer is : Distance between points P and Q is 13.

Suppose the coordinates of point T are (x₁, y₁) and of point R are (x₂, y₂).

x₁ = −3, y₁ = 6, x₂ = 9 and y₂ = −10

By distance formula,

PQ = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{[9-(-3)]^2+(-10-6)^2}$

= $\sqrt{(12)^2+(-16)^2}$

= $\sqrt{144 + 256}$

= $\sqrt{400}$

= 20

Answer is : Distance between points P and Q is 20.

Suppose the coordinates of point W are (x₁, y₁) and of point X are (x₂, y₂).

x₁ = $\frac{-7}{2}$, y₁ = 4, x₂ = 11 and y₂ = 4

By distance formula,

PQ = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{[11-(\frac{-7}{2})]^2+(4-4)^2}$

= $\sqrt{(11+\frac{7}{2})^2+(0)^2}$

= $\sqrt{(\frac{22+7}{2})^2 + 0}$

= $\sqrt{(\frac{29}{2})^2}$

= $\frac{29}{2}$

= 14.5

Answer is : Distance between points P and Q is 14.5.

Given : A(1, −3), B(2, −5), C(−4, 7)

By distance formula,

d(A, B) = $\sqrt{(2-1)^2+[(-5-(-3)]^2}$

= $\sqrt{(1)^2+(-2)^2}$

= $\sqrt{1 + 4}$

= $\sqrt{5}$        ….(i)

d(B, C) = $\sqrt{(-4-2)^2+[(7-(-5)]^2}$

= $\sqrt{(-6)^2+(12)^2}$

= $\sqrt{36+144}$

= $\sqrt{180}$

= $\sqrt{36×5}$

= $6\sqrt{5}$          ….(ii)

d(A, C) =  $\sqrt{(-4-1)^2+[(7-(-3)]^2}$

= $\sqrt{(-5)^2+(10)^2}$

= $\sqrt{25+100}$

= $\sqrt{125}$

= $\sqrt{25×5}$

= $5\sqrt{5}$           ….(iii)

Adding (i) and (iii),

d(A, B) + d(A, C)= $\sqrt{5}$  + $5\sqrt{5}$ = $6\sqrt{5}$   ... (iv)

∴ d(A, B) + d(A, C) = d(B, C)        ... [From (ii) and (iv)]

∴ points A, B and C are collinear.

Answer is: Points A(1, −3), B(2, −5) and C(−4, 7) are collinear.

Given : L(−2, 3), M(1, −3), N(5, 4)

By distance formula,

d(L, M) = $\sqrt{[1-(-2)]^2+(-3-3)^2}$

= $\sqrt{(3)^2+(-6)^2}$

= $\sqrt{9 + 36}$

= $\sqrt{45}$

= $\sqrt{9×5}$

= $3\sqrt{5}$       ….(i)

d(M, N) = $\sqrt{(5-1)^2+[4-(-3)]^2}$

= $\sqrt{(4)^2+(7)^2}$

= $\sqrt{16 + 49}$

= $\sqrt{65}$   ….(ii)

d(L, N) = $\sqrt{[5-(-2)]^2+(4-3)^2}$

= $\sqrt{(7)^2+(1)^2}$

= $\sqrt{49 + 1}$

= $\sqrt{50}$

= $\sqrt{25×2}$

= $5\sqrt{2}$         ….(iii)

Adding (i) and (iii),

d(L, M) + d(L, N) = $3\sqrt{5}$ + $5\sqrt{2}$   ….(iv)

∴ d(L, M) + d(L, N) ≠ d(M, N)   ….[From (ii) and (iv)]

∴ points L, M and N are not collinear.

Answer is: Points L(−2, 3), M(1, −3) and N(5, 4) are not collinear.

Given : R(0, 3), D(2, 1), S(3, −1)

By distance formula,

d(R, D) = $\sqrt{(2-0)^2+(1-3)^2}$

= $\sqrt{(2)^2+(-2)^2}$

= $\sqrt{4 + 4}$

= $\sqrt{8}$

= $\sqrt{4×2}$

= $2\sqrt{2}$       ….(i)

d(D, S) = $\sqrt{(3-2)^2+(-1-1)^2}$

= $\sqrt{(1)^2+(-2)^2}$

= $\sqrt{1 + 4}$

= $\sqrt{5}$         ….(ii)

d(R, S) = $\sqrt{(3-0)^2+(-1-3)^2}$

= $\sqrt{(3)^2+(-4)^2}$

= $\sqrt{9 + 16}$

= $\sqrt{25}$

= 5      ….(iii)

Adding (ii) and (iii),

d(D, S) + d(R, S) = $\sqrt{5}$ + 5    ….(iv)

∴ d(D, S) + d(R, S) ≠ d(R, D)     ... [From (i) and (iv)]

∴ points R, D and S are not collinear.

Answer is . Points R(0, 3), D(2, 1) and S(3, −1) are not collinear.

Given : P(−2, 3), Q(1, 2), R(4, 1)

By distance formula,

d(P, Q) = $\sqrt{[1-(-2)]^2+(2-3)^2}$

= $\sqrt{(3)^2+(-1)^2}$

= $\sqrt{9 + 1}$

= $\sqrt{10}$      ….(i)

d(Q, R) = (\sqrt{(4-1)^2+(1-2)^2}\)

= $\sqrt{(3)^2+(-1)^2}$

= $\sqrt{9 + 1}$

= $\sqrt{10}$        ….(ii)

d(P, R) = $\sqrt{[4-(-2)]^2+(1-3)^2}$

= $\sqrt{(6)^2+(-2)^2}$

= $\sqrt{36 + 4}$

= $\sqrt{40}$

= $\sqrt{4×10}$

= $2\sqrt{10}$      ….(iii)

Adding (i) and (ii), we get,

d(P, Q) + d(Q, R) = $\sqrt{10}$ + $\sqrt{10}$

∴ d(P, Q) + d(Q,R) = $2\sqrt{10}$      ….(iv)

∴ d(P, Q) + d(Q, R) = d(P, R)   ... [From (iii) and (iv)]

∴ points P, Q and R are collinear.

Answer is: Points P(−2, 3), Q(1, 2) and R(4, 1) are collinear.

A(−3, 4) and B(1, − 4).

Let P be the point on X−axis equidistant from points A and B.

PA = PB      …..(i)

P lies on X−axis  its y coordinate is 0.

Let P(x, 0)

Now PA = PB       ….[From (i)]

By distance formula,

d(P, A) = d(P, B)

$\sqrt{[x-(-3)]^2+(0-4)^2}$ = $\sqrt{(x-1)^2+[0-(-4)]^2}$

∴ $\sqrt{(x+3)^2+(-4)^2}$ = $\sqrt{(x-1)^2+(4)^2}$

∴ $\sqrt{(x+3)^2+16}$ = $\sqrt{(x-1)^2+16}$

Squaring both the sides,

(x + 3)² + 16 = (x − 1)² + 16

X² + 6x + 9 = x² − 2x + 1

6x + 2x = 1 — 9

8x = − 8

∴ x = −8/8

∴ x = − 1

P(−1, 0)

Answer is: The coordinates of point on X−axis equidistant from points A and B are ( −1, 0).

Given : P( −2, 2), Q(2, 2) and R(2, 7)

By distance formula,

PQ = $\sqrt{[2-(-2)]^2+(2-2)^2}$

= $\sqrt{(4)^2+(0)^2}$

= $\sqrt{16 + 0}$

= $\sqrt{16}$

= 4                         ….(i)

QR = $\sqrt{(2-2)^2+(7-2)^2}$

= $\sqrt{(0)^2+(5)^2}$

= $\sqrt{0 + 25}$

= $\sqrt{25}$

= 5   ….(ii)

PR = $\sqrt{[2-(-2)]^2+(7-2)^2}$

= $\sqrt{(4)^2+(5)^2}$

= $\sqrt{16 + 25}$

= $\sqrt{41}$

PQ² + QR² = 4² + 5² = 16 + 25 = 41   …. [From (i) and (ii)] ….(iii)

PR² = $(\sqrt{41})^2$ = 41   ….(iv)

PQ² + QR² = PR²    ….[From (iii) and (iv)]

by converse of Pythagoras theorem, Δ PQR is a right angled triangle.

i.e. P( −2, 2), Q(2, 2) and R(2, 7) are the vertices of a right angled triangle.

Given : P(2, −2), Q(7, 3), R(11, −1) and S (6, −6)

By distance formula,

PQ = $\sqrt{(7-2)^2+[3-(-2)]^2}$

= $\sqrt{(5)^2+(5)^2}$

= $\sqrt{25 + 25}$

= $\sqrt{50}$

= $\sqrt{25×2}$

= $5\sqrt{2}$       ….(i)

QR = $\sqrt{(11-7)^2+(-1-3)^2}$

= $\sqrt{(4)^2+(-4)^2}$

= $\sqrt{16 + 16}$

= $\sqrt{32}$

= $\sqrt{16×2}$

= $4\sqrt{2}$       ….(ii)

RS = $\sqrt{(6-11)^2+[-6-(-1)]^2}$

= $\sqrt{(-5)^2+(-5)^2}$

= $\sqrt{25 + 25}$

= $\sqrt{50}$

= $\sqrt{25×2}$

= $5\sqrt{2}$      ….(iii)

PS = $\sqrt{(6-2)^2+[-6-(-2)]^2}$

= $\sqrt{(4)^2+(-4)^2}$

= $\sqrt{16 + 16}$

= $\sqrt{32}$

= $\sqrt{16×2}$

= $4\sqrt{2}$        ….(iv)

ln □ PQRS.

PQ = RS  [From (i) and (iii)]

OH = PS '  [From (ii) and (iv)]

A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent.

∴ □ PQRS is a parallelogram.

P(2, −2), Q(7, 3), R(11, −1) and S(6, −6) are vertices of a parallelogram.

Given : A(−4, −7), B(−1, 2), C(8, 5) and D(5, −4)

By distance formula,

d(A, B) = $\sqrt{[-1-(-4)]^2+[2-(-7)]^2}$

= $\sqrt{(3)^2+(9)^2}$

= $\sqrt{9+81}$

= $\sqrt{90}$

= $\sqrt{9×10}$

= $3\sqrt{10}$

∴ AB = $3\sqrt{10}$        ….(i)

d(B, C) = $\sqrt{[8-(-1)]^2+(5-2)^2}$

= $\sqrt{(9)^2+(3)^2}$

= $\sqrt{81+9}$

= $\sqrt{90}$

= $\sqrt{9×10}$

= $3\sqrt{10}$

∴ BC = \(3\sqrt{10}\        ….(ii)

d(C, D) = $\sqrt{(5-8)^2+(-4-5)^2}$

= $\sqrt{(-3)^2+(-9)^2}$

= $\sqrt{9+81}$

= $\sqrt{90}$

= $\sqrt{9×10}$

= $3\sqrt{10}$

∴ CD = $3\sqrt{10}$          ….(iii)

d(A, D) = $\sqrt{[5-(-4)]^2+[-4-(-7)]^2}$

= $\sqrt{(9)^2+(3)^2}$

= $\sqrt{81+9}$

= $\sqrt{90}$

= $\sqrt{9×10}$

= $3\sqrt{10}$

∴ AD = $3\sqrt{10}$        ….(iv)

from (i), (ii), (iii) and (iv)

AB = BC = CD = AD

□ ABCD is a rhombus.

∴ A(−4, −7), B(−1, 2), C(8, 5) and D(5. −4) are vertices of rhombus ABCD.

Given : L(x, 7) and M(1, 15) d(L, M) = 10

By distance formula,

d(L, M) = $\sqrt{(x-1)^2+(7-15)^2}$

∴ 10 = $\sqrt{(x-1)^2+(-8)^2}$

Squaring both the sides, we get,

100 = (x − 1)² + 64

∴ (x − 1)² = 100 − 64

∴ (x − 1)² = 36

∴ x − 1 = ± 6      …. (Taking square roots of both the sides)

Either x – 1 = 6 or x – 1 = −6

∴ x = 6 + 1 or x = −6 + 1

∴ x = 7 or x = −5

Answer is x = 7 or x = −5.

Given : A(1, 2), B(1, 6), C(1+$2\sqrt{3}$, 4)

By distance formula,

AB = $\sqrt{(1-1)^2+(6-2)^2}$

= $\sqrt{(0)^2+(4)^2}$

= $\sqrt{0+16}$

= $\sqrt{16}$

= 4

BC = $\sqrt{(1+2\sqrt{3}-1)^2+(4-6)^2}$

= $\sqrt{(2\sqrt{3})^2+(-4)^2}$

= $\sqrt{12+4}$

= $\sqrt{16}$

= 4    ….(ii)

AC = $\sqrt{(1+2\sqrt{3}-1)^2+(4-2)^2}$

= $\sqrt{(2\sqrt{3})^2+(2)^2}$

= $\sqrt{12+4}$

= $\sqrt{16}$

= 4

∴ AB = BC = AC

∴ Δ ABC is an equilateral triangle.

∴ All, A(1, 2), B(1, 6), C(1+ , 4) are vertices of an equilateral triangle,

A(−1, 7) and B(4, −3).

Let the coordinates of point P be (x, y).

Suppose coordinates of point A are (x₁, y₁) and B are (x₂, y₂) then

x₁ = −1, y₁ = 7, x₂ = 4 and y₂ = −3.

P divides AB in the ratio 2 : 3.

∴ m : n = 2 : 3

By section formula,

x = $\frac{mx_2+nx_1}{m+n}$

∴ x = $\frac{2(4)+3(-1)}{2+3}$ = $\frac{8-3}{5}$ = $\frac{5}{5}$ = 1

y = $\frac{my_2+ny_1}{m+n}$

∴ y = $\frac{2(-3)+3(7)}{2+3}$ = $\frac{-6+21}{5}$ = $\frac{15}{5}$  = 3

P(1, 3) divides the line segment joining the points A(−1, 7) and B(4, −3) in the ratio 2 : 3.

P(−3, 7) and Q(1, − 4).

Let coordinates of point A be (x, y).

Suppose coordinates of point P are (x₁, y₁) and Q are (x₂, y₂)

then x₁ = −3, y₁ = 7, x₂ = 1 and y₂ = −4.

A divides PQ in the ratio a : b.

a : b = 2 : 1.

By section formula,

x = $\frac{ax_2+bx_1}{a+b}$

∴ x = $\frac{2(1)+1(-3)}{2+1}$ = $\frac{2-3}{3}$ = $-\frac{1}{3}$

y = $\frac{ay_2+by_1}{a+b}$

∴ x = $\frac{2(-4)+1(7)}{2+1}$ = $\frac{-8+7}{3}$ = $-\frac{1}{3}$

∴ the co−ordinates of point A are $(-\frac{1}{3},\,-\frac{1}{3})$

P(−2, −5), Q(4, 3), a : b = 3 : 4

Let coordinates of point A be (x, y).

Suppose coordinates of point P are (x₁, y₁) and Q are (x₂, y₂)

then x₁ = −2, y₁ = −5, x₂ = 4 and y₂ = 3.

A divides PQ in the ratio a : b.

a : b = 3 : 4.

By section formula,

x = $\frac{ax_2+bx_1}{a+b}$

∴ x = $\frac{3(4)+4(-2)}{3+4}$ = $\frac{12-8}{7}$ = $\frac{4}{7}$

y = $\frac{ay_2+by_1}{a+b}$

∴ y = $\frac{3(3)+4(-5)}{3+4}$ = $\frac{9-20}{7}$ = $-\frac{11}{7}$

∴ the co−ordinates of point A are $(\frac{4}{7},\,-\frac{11}{7})$

P(2, 6), Q(−4, 1), a : b = 1 : 2

Let coordinates of point A be (x, y).

Suppose coordinates of point P are (x₁, y₁) and Q are (x₂, y₂)

then x₁ = 2, y₁ = 6, x₂ = −4 and y₂ = 1.

A divides PQ in the ratio a : b.

a : b = 1 : 2.

By section formula,

x = $\frac{ax_2+bx_1}{a+b}$

∴ x = $\frac{1(-4)+2(2)}{1+2}$ = $\frac{-4+4}{3}$ = $\frac{0}{3}$ = 0

y = $\frac{ay_2+by_1}{a+b}$

∴ y = $\frac{1(1)+2(6)}{1+2}$ = $\frac{1+12}{3}$ = $\frac{13}{3}$

∴ the co−ordinates of point A are (0, $\frac{13}{3}$)

P(−3, 10), Q(6, −8) and T(−1, 6).

Suppose the coordinates of point P are (x₁, y₁), the coordinates of point Q are (x₂, y₂) and the coordinates of point T are (x, y).

Here, x₁ = −3, y₁ = 10, x₂ = 6, y₂ = −8, x = −1 and y = 6

By section formula,

x = $\frac{mx_2+nx_1}{m+n}$

∴ −1 = $\frac{m(6)+n(-3)}{m+n}$

∴ −1(m + n) = 6m – 3n

∴ −m − n = 6m – 3n

∴ 7m = 2n

∴ $\frac{m}{n}=\frac{2}{7}$

∴ m : n = 2 : 7

Answer is : T divides line segment PQ in the ratio 2 : 7.

A(2, −3) and P(−2, 0). Let B(x, y).

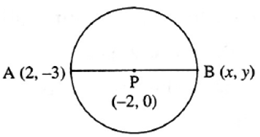
The centre of the circle is the midpoint of the diameter.

∴  by midpoint formula,

−2 = $\frac{2+x}{2}$

∴ −4 = 2 + x

∴ x = −6

and 0 = $\frac{-3+y}{2}$

∴ −3 + y = 0

∴ y = 3

Answer is: The coordinates of point B are (−6, 3).

A(8, 9), B(1, 2) and P(k, 7).

Let P divide the seg AB in the ratio m : n.

Here, x₁ = 8, y₁ = 9, x₂ = 1, y₂ = 2, x = k and y = 7

By section formula,

y = $\frac{m(2)+n(9)}{m+n}$

∴ 7 = $\frac{2m+9n}{m+n}$

∴ 7(m + n) = 2m + 9n

∴ 7m + 7n = 2m + 9n

∴ 7m − 2m = 9n − 7n

∴ 5m = 2n

∴ $\frac{m}{n}=\frac{2}{5}$

∴ m : n = 2 : 5

P divides segment AB in the ratio 2 : 5.

By section formula,

k = $\frac{2(1)+5(8)}{2+5}$ = $\frac{2+40}{7}$ = 6

Answer is: The ratio in which point P divides seg AB is 2 : 5 and value of k is 6.

Let A(22, 20) and B(0, 16).

Let P(x, y) be its midpoint of seg AB.

If A(x₁, y₁) and B(x₂, y₂)

then x₁ = 22, y₁ = 20, X₂ = 0 and y₂ = 16

By midpoint formula,

x = $\frac{x_1+x_2}{2}$ and y = $\frac{y_1+y_2}{2}$

∴ x = $\frac{22+0}{2}$ = 11  and y = $\frac{20+16}{2}$ = 18

Answer is: Coordinates of midpoint of the segment joining the points (22, 20) and (0, 16) are (11, 18).

Let A(−7, 6), B(2, −2) and C(8, 5).

Suppose the coordinates of point A are (x₁, y₁), coordinates of point B are (x₂, y₂) and coordinates of point C are (x₃, y₃).

∴ x₁ = −7, y₁ = 6, x₂ = 2, y₂ = −2, x₃ = 8 and y₃ = 5.

Let O(x, y) be the centroid.

By centroid formula,

x = $\frac{x_1+x_2+x_3}{3}$  and y = $\frac{y_1+y_2+y_3}{3}$

∴ x = $\frac{-7+2+8}{3}$ = $\frac{3}{3}$ = 1 and y = $\frac{6+(-2)+5}{3}$ = $\frac{9}{3}$ = 3

Answer is : The coordinates of the centroid are (1, 3).

Let A(3, −5), B(4, 3) and C(11, −4).

Suppose the coordinates of point A are (x₁, y₁), coordinates of point B are (x₂, y₂) and coordinates of point C are (x₃, y₃).

∴ x₁ = 3, y₁ = −5, x₂ = 4, y₂ = 3, x₃ = 11 and y₃ = −4.

Let O(x, y) be the centroid.

By centroid formula,

x = $\frac{x_1+x_2+x_3}{3}$  and y = $\frac{y_1+y_2+y_3}{3}$

∴ x = $\frac{3+4+11}{3}$ = $\frac{18}{3}$ = 6  and y = $\frac{-5+3+(-4)}{3}$ = $\frac{-6}{3}$  = −2

Answer is : The coordinates of the centroid are (6, −2).

Let A(4, 7), B(8, 4) and C(7, 11).

Suppose the coordinates of point A are (x₁, y₁), coordinates of point B are (x₂, y₂) and coordinates of point C are (x₃, y₃).

∴ x₁ = 4, y₁ = 7, x₂ = 8, y₂ = 4, x₃ = 7 and y₃ = 11.

Let O(x, y) be the centroid.

By centroid formula,

x = $\frac{x_1+x_2+x_3}{3}$  and y = $\frac{y_1+y_2+y_3}{3}$

∴ x = $\frac{4+8+7}{3}$ = $\frac{19}{3}$ and y = $\frac{7+4+11}{3}$ = $\frac{22}{3}$

Answer is : The coordinates of the centroid are ( $\frac{19}{3}$, $\frac{22}{3}$).

A(−14, −19), B(3,5) and G(−4, −7)

Suppose the coordinates of point A are (x₁, y₁), coordinates of point B are (x₂, y₂) coordinates of point C are (x₃, y₃) and coordinates of point G are (x, y).

Here, x₁ = −14, y₁ = −19, x₂ = 3, y₂ = 5, x = − 4, y = −7.

By centroid formula,

x = $\frac{x_1+x_2+x_3}{3}$

∴ −4 = $\frac{-14+3+x_3}{3}$ 

∴ −4 × 3 = −11 + x₃

∴ −12 = −11 + x₃

∴ x₃ = −1

y = $\frac{y_1+y_2+y_3}{3}$

∴ −7 = $\frac{-19+5+y_3}{3}$

∴  −7 × 3 = −14 + y₃

∴ −21 + 14 = y₃

∴ y₃ = −7

Answer is : The coordinates of C are (−1, −7).

A(h, −6), B(2,3), C(−6, k) and G(1, 5).

Suppose the coordinates of point A are (x₁, y₁), coordinates of point B are (x₂, y₂) coordinates of point C are (x₃, y₃) and coordinates of point G are (x, y).

Here, x₁ = h, y₁ =− 6, x₂ = 2, y₂ = 3, x₃ = −6, y₃ = k, x = 1 and y = 5.

By centroid formula,

x = $\frac{x_1+x_2+x_3}{3}$

∴ 1 = $\frac{h+2+(-6)}{3}$  

∴ 1 × 3 = h − 4

∴ 3 + 4 = h

∴ h = 7

y = $\frac{y_1+y_2+y_3}{3}$

∴ 5 = $\frac{-6+3+k}{3}$

∴  5 × 3 = −3 + k

∴ 15 + 3 = k

∴ k = 18

Answer is : h = 7 and k = 18

A(2,7) and B(−4, −8)

Let P(x₁, y₁) and Q(x₂, y₂) be the points of trisection.

∴ AP = PQ = QB    ….(i)

∴ $\frac{AP}{PB}$ = $\frac{AP}{PQ+QB}$         ….(P—Q—B)

∴ $\frac{AP}{PB}$ = $\frac{AP}{AP+AP}$       ….[from (i)]

∴ $\frac{AP}{PB}$ = $\frac{AP}{2AP}$

∴ AP : PB = 1 : 2

∴ P divides segment AB in the ratio 1 : 2.

By section formula for ratio m : n

x₁ = $\frac{1(-4)+2(2)}{1+2}$ = $\frac{-4+4}{3}$ = 0

and y₁ = $\frac{1(-8)+2(7)}{1+2}$ = $\frac{-8+14}{3}$ = $\frac{6}{3}$ = 2

∴ x₁  = 0 and y₁  = 2

∴ the coordinates of point P are (0, 2).

AP = PQ    ….[from (i)]

∴ P(x₁, y₁) is the midpoint of AQ.

By midpoint formula,

x₁ = $\frac{x_2+2}{2}$ and y₁ = $\frac{y_2+7}{2}$

∴ 0 = $\frac{x_2+2}{2}$ and 2 = $\frac{y_2+7}{2}$

∴ x₂ = −2  and y₂ = −3

∴ the coordinates of point Q are (−2, −3).

Answer is: The coordinates of the points of trisection of the line segment AB are (0, 2) and (−2. −3).

A(−14, −10) and B(6, −2)

Let P, Q and R be the points that divide segment AB into four equal parts.

Let P(x₁, y₁), Q(x₂, y₂) and R(x₃, y₃).

Q is the midpoint of seg AB.

∴ by midpoint formula,

x₂ = $\frac{-14+6}{2}$ = $\frac{-8}{2}$ = −4

y₂ = $\frac{-10+(-6)}{2}$ = $\frac{-12}{2}$ = −6

The coordinates of point Q are (−4, −6).

P is the midpoint of seg AQ.

∴ by midpoint formula,

x₁ = $\frac{-14+(-4)}{2}$ = $\frac{-18}{2}$ = −9

y₁ = $\frac{-10+(-6)}{2}$ = $\frac{-16}{2}$ = −8

∴ the coordinates of point P are (−9, −8).

R is the midpoint of seg QB.

∴ by midpoint formula,

x₃ = $\frac{-4+6)}{2}$ = $\frac{2}{2}$ = 1

y₃ = $\frac{-6+(-2)}{2}$ = $\frac{-8}{2}$ = −4

∴ the coordinates of point R are (1, −4).

Answer is: The coordinates of the points which divide segment AB into four equal parts are (−9, −8), (−4, −6) and (1, − 4).

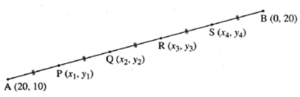
A(20, 10) and B(0, 20).

Let points P(x1, y1), Q(x2, y2), R(X3, y3) and S(x4, y4)

divide seg AB into five congruent parts.

∴ AP = PQ = QR = RS = SB     ... (1)

∴ $\frac{AP}{PB}$ = $\frac{AP}{PQ+QR+RS+SB}$         ….(P—Q—R, Q—R—S, R—S—B,)

∴ $\frac{AP}{PB}$ = $\frac{AP}{4AP}$

∴ AP : PB = 1 : 4

∴ P divides AB in the ratio 1 : 4.

By section formula,

∴ x₁ = $\frac{(1)(0)+4(20)}{1+4}$ = $\frac{80}{5}$ = 16

and y₁ = $\frac{(1)(20)+4(10)}{1+4}$ = $\frac{60}{5}$ = 12

∴ the coordinates of point P are (16, 12).

P is the midpoint of seg AQ,

∴ by midpoint formula,

∴ the coordinates of point Q are (12, 14).

R is the midpoint of seg PB.

∴ by midpoint formula,

∴ the coordinates of point R are (8, 16).

S is the midpoint of seg RB.

∴ by midpoint formula,

∴ the coordinates of point S are (4, 18).

Answer is: (16, 12), (12, 14), (8, 16) and (4, 18) are the coordinates of the points which divide segment AB into five congruent parts.

Angle made by the line with the positive direction of X−axis (θ) = 45°

Slope of the line (m) = tan θ = tan 45° = 1

Answer is: Slope of the given line is 1.

Angle made by the line with the positive direction of X−axis (θ) = 60°

Slope of the line (m) = tan θ = tan 60° =

Answer is: Slope of the given line is .

Angle made by the line with the positive direction of X−axis (θ) = 90°

Slope of the line (m) = tan θ = tan 90°

tan 90° is not defined

Answer is: Slope of the given line is not defined

A(2, 3) and B(4, 7)

Let A (x₁, y₁) and B(x₂, y₂)

then x₁ = 2, y₁ = 3, x₂ = 4, y₂ = 7

Slope of line AB = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{7-3}{4-2}$ = $\frac{4}{2}$ = 2

Answer is: Slope of line AB is 2.

P(−3, 1) and Q(5, −2)

Let P(x₁, y₁) and Q(x₂, y₂)

then x₁ = −3, y₁ = 1, x₂ = 5, y₂ = −2

Slope of line PQ = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{-2-(-1)}{5-(-3)}$ = $\frac{-3}{8}$

Answer is: Slope of line PQ is $\frac{-3}{8}$ .

C(5, −2) , D(7, 3)

Let C(x₁, y₁) and D(x₂, y₂)

then x₁ = 5, y₁ = −2, x₂ = 7, y₂ = 3

Slope of line CD = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{-3-(-2)}{7-5}$ = $\frac{5}{2}$

Answer is: Slope of line CD is $\frac{5}{2}$ .

L(−2, −3), M(−6, −8)

Let L(x₁, y₁) and M(x₂, y₂)

then x₁ = −2, y₁ = −3, x₂ = −6, y₂ = −8

Slope of line LM = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{-8-(-3)}{-6-(-2)}$ = $\frac{-5}{-4}$ = $\frac{5}{4}$

Answer is: Slope of line LM is $\frac{5}{4}$ .

E(−4, −2) , F(6, 3)

Let E(x₁, y₁) and F(x₂, y₂)

then x₁ = −4, y₁ = −2, x₂ = 6, y₂ = 3

Slope of line EF = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{3-(-2)}{6-(-4)}$ = $\frac{5}{10}$ = $\frac{1}{2}$

Answer is: Slope of line EF is $\frac{1}{2}$ .

T(0, −3), S(0, 4)

Let T(x₁, y₁) and S(x₂, y₂)

then x₁ = 0, y₁ = −3, x₂ = 0, y₂ = 4

Slope of line TS = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{4-(-3)}{0-0}$ = $\frac{7}{0}$ which is not defined

Answer is: Slope of line TS cannot determined.

A(−1, −1), B(0, 1), C(1, 3)

Slope of line AB = $\frac{1-(-1)}{0-(-1)}$ = $\frac{2}{1}$ = 2

Slope of line BC = $\frac{3-1}{1-0}$ = $\frac{2}{1}$ = 2

Slope of line AB = slope of line BC and B is the common point.

∴ points A, B and C are collinear.

Answer is: Points A(−1, −1), B(0, 1) and C(1, 3) are collinear.

D(−2, −3), E(1, 0), F(2, 1)

Slope of line DE = $\frac{0-(-3)}{1-(-2)}$ = $\frac{3}{3}$ = 1

Slope of line EF = $\frac{1-0}{2-1}$ = $\frac{1}{1}$ = 1

Slope of line DE = slope of line EF and E is the common point.

∴ points D, E and F are collinear.

Answer is: Points D(−2, −3), E(1, 0) and F(2, 1) are collinear.

L(2, 5), M(3, 3), N(5, 1)

Slope of line LM = $\frac{3-5}{3-2}$ = $\frac{-2}{1}$ = −2

Slope of line MN = $\frac{1-3}{5-3}$ = $\frac{-2}{2}$ = −1

Slope of line LM ≠ slope of line MN

∴ points L, M and N are not collinear.

Answer is: Points L(2, 5), M(3, 3) and N(5, 1) are not collinear.

P(2, −5), Q(1, −3), R(−2, 3)

Slope of line PQ = $\frac{-3-(-5)}{1-2}$ = $\frac{2}{-1}$  = −2

Slope of line QR = $\frac{3-(-3)}{-2-1}$ = $\frac{6}{-3}$ = −2

Slope of line PQ = slope of line QR and Q is the common point.

∴ points P, Q and R are collinear.

Answer is: Points P(2, −5), Q(1, −3) and R(−2, 3) are collinear.

R(1, −4), S(−2, 2), T(−3, 4)

Slope of line RS = $\frac{2-(-4)}{-2-1}$ = $\frac{6}{-3}$ = −2

Slope of line ST = $\frac{4-2}{-3-(-2)}$ = $\frac{2}{-1}$ = −2

Slope of line RS = slope of line ST and S is the common point.

∴ points R, S and T are collinear.

Answer is: Points R(1, −4), S(−2, 2) and T( −3, 4) are collinear.

A(−4, 4), K(−2, $\frac{5}{2}$), N(4, −2)

Slope of line AK = $\frac{\frac{5}{2}-4}{-2-(-4)}$ = $\frac{-3/2}{2}$ = $-\frac{3}{4}$

Slope of line KN = $\frac{-2-\frac{5}{2}}{4-(-2)}$ = $\frac{-9/2}{6}$ = $-\frac{-9}{12}$ = $-\frac{3}{4}$

Slope of line AK = slope of line KN and K is the common point.

∴ points A, K and N are collinear.

Answer is: Points A(−4, 4), K(−2,  ) and N(4, −2) are collinear.

A(1, −1), B(0, 4), C(−5, 3)

Slope of side AB = $\frac{4-(-1)}{0-1}$ = $\frac{5}{-1}$ = −5

Slope of side BC = $\frac{3-4}{-5-0}$ = $\frac{-1}{-5}$ = $\frac{1}{5}$

Slope of side AC = $\frac{3-(-1)}{-5-1}$ = $\frac{4}{-6}$ = $-\frac{1}{3}$

Answer is : Slope of side AB is −5, slope of side BC is $\frac{1}{5}$  , slope of side AC is $-\frac{1}{3}$ 

A(−4, −7), B(−1, 2), C(8, 5) and D(5, −4)

Slope of side AB = $\frac{2-(-7)}{-1-(-4)}$ = $\frac{9}{3}$ = 3      ……(i)

Slope of side BC = $\frac{5-2}{8-(-1)}$ = $\frac{3}{9}$ = $\frac{1}{3}$      ……(ii)

Slope of side CD = $\frac{-4-5}{5-8}$ = $\frac{-9}{-3}$ = 3      ……(iii)

Slope of side AD = $\frac{-4-(-7)}{5-(-4)}$ = $\frac{3}{9}$ = $\frac{1}{3}$       ……(iv)

From (i) and (iii),

Slope of line AB = slope of line CD

∴ line AB || line CD   ….(If two lines have equal slopes then they are parallel)

From (ii) and (iv),

Slope of line BC = slope of line AD

∴ line BC || line AD   ….(If two lines have equal slopes then they are parallel)

∴ □ ABCD is a parallelogram. A(−4, −7), B(−1, 2), C(8, 5) and D(5, −4) are the vertices of a parallelogram.

R(1, −1) and S(−2, k)

Slope of line RS = −2

Slope of side RS = $\frac{k-(-1)}{-2-1}$ 

∴ -2 = $\frac{k+1}{-3}$ 

∴ -2 × -3 = k + 1

∴ 6 = k + 1

∴ k = 6 – 1 = 5

Answer is: The value of k is 5

B(k, −5), C (1, 2)

Slope of the line BC = 7

Slope of the line BC = $\frac{2-(-5)}{1-k}$

∴ 7 = $\frac{7}{1-k}$

∴ 7(1 – k) = 7

∴ 1 − k = 1

∴ k = 1 – 1 = 0

Answer is: The value of k is 0

Given : Line PQ || line RS.

P(2, 4), Q (3, 6), R(3, 1), S(5, k)

Parallel lines have equal slopes,

∴  slope of line PQ = slope of line RS

∴ $\frac{6-4}{3-2}$ = $\frac{k-1}{5-3}$

∴ $\frac{2}{1}$ = $\frac{k-1}{2}$

∴ 4 = k – 1

∴ k = 4 + 1 = 5

Answer is: The value of k is 5