Electrochemistry
Maharashtra Board-Class-12-Chemistry-Chapter-5
Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Electrolysis : Electrolysis is breaking down of an ionic compound by the passage of electricity.
Electrochemistry : It is a branch of physical chemistry that studies the relationship between chemical changes and electrical energy, as well as the electrical properties of electrolytic solutions such as resistance and conductance.
- Electrolysis may be the only way to produce fluorine.
- Electrochemical processes include electro-refining (for metal purification) and electroplating (for coating one metal on the surface of another).
Electric conduction :
Electric conduction : The transfer of electric charge or electrons from one point to another is called electric conduction which results in an electric current.
Electric conductors :
The substances that allow the flow of electricity or electric charge transfer through them are called the ' electric conductors.
Flow of electricity or a transfer of electric charge :
The transfer of electrons from one point to another is involved in the flow of electricity or the transfer of electric charge through a conductor. This occurs as a result of the applied electric potential.
Types of electric conductors :
The electric conductors are classified according to the mechanism of the transfer of electrons or charge.
There are two types of conductors as follows :
(i) Electronic (or metallic) conductors : The electric conductors through which the conduction of electricity takes place by a direct flow of electrons under the influence of applied potential are called electronic conductors.
The outermost electrons of metals form conduction bond. The electrons in conduction band are free to move and hence flow under the influence of applied electrical potential. Metallic conductors are, thus, electronic conductors.
Characteristics of metallic conductors :
- The conduction does not involve the transfer of a matter.
- No chemical change is involved during conduction.
- The resistance of the conductor increases and conductivity decreases with the increase in temperature.
- The conductance of metallic conductors is very high.
- Examples are solid or molten metals, such as Al, Cu. etc.
(ii) Electrolytic conductors : Electrolytic conductors are conductors that conduct electricity through the migration of positive ions (cations) and negative ions (anions) of the electrolyte.
Characteristics of electrolytic conductors :
- The conduction involves the transfer of a matter.
- Chemical changes are always involved during the passage of an electric current.
- The resistance decreases and the conductivity increases with the increase in temperature.
- The conductance of the electrolytes is comparatively low.
- Examples are aqueous solutions of acids, bases or salts.
Information provided by measurement of conductivities of solutions :
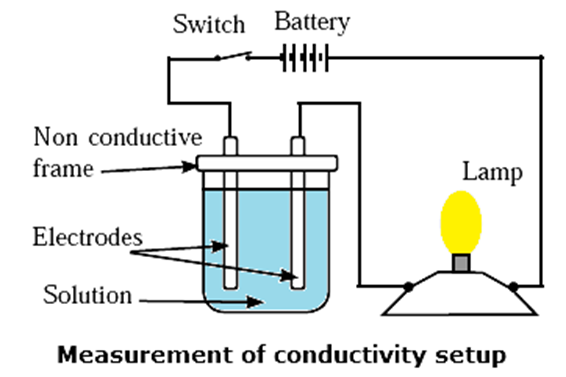
The lamp will glow when circuit is complete in above setup.
Conductivity cell : A cell or a device used to measure the conductance of a solution is called a conductivity cell.
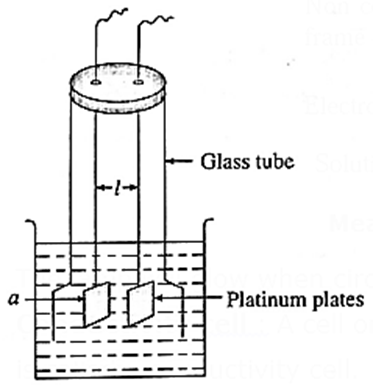
Cell constant : Cell constant of a conductivity cell is defined as the ratio of the distance between the electrodes divided by the area of cross section of the electrodes.
If a is the cross section area of two platinum plates at l distance apart in the conductivity cell, then for any given conductivity cell, the ratio, l/a is constant which is called cell constant.
∴ Cell constant = b = l/a cm-1
In SI units it is expressed as m-1
Following information is provided by measurement of conductivities of solutions :
- The conducting and nonconducting properties of solutions can be identified by the measurement of their conductivities.
- The substances like sucrose and urea which do not dissociate in aqueous solutions have same conductivity as that of water. Hence they are nonelectrolytes.
- The substances like KCl, CH3COOH, NaOH, etc. dissociate in their aqueous solutions and their conductivities are higher than water. Hence they are electrolytes.
- On the basis of high or low electrical conductivity, the electrolytes can be classified as strong and weak electrolytes. The solutions of strong electrolytes have high conductivities while solutions of weak electrolytes have lower conductivities.
Remember : Electrolyte is a compound that conducts electricity when molten or in aqueous solution and breaks down into ions during electrolysis.
Electrical conductance of solution :
Ohm’s Law : According to Ohm’s law, the electrical resistance R of a conductor is equal to the electric potential difference V divided by the electric current.
R = V/I ohm
The unit of electrical resistance is ohm denoted by the symbol Ω (omega).
The SI unit of potential is volt denoted by V.
The SI unit of electric current is ampere denoted by A.
Thus, Ω = VA−1.
Electrical conductance : The reciprocal of the electrical resistance of a solution is called the conductance. It is represented by G.
Conductance (G) = 1/Resistance = 1/R
The conductance has units of reciprocal of ohm (Ω-1, ohm-1 or mho).
In SI units, conductance has units as Siemens, (S).
1 S = 1 Ω−1 = l ohm−1 = 1 mho =AV−1 = CV−1S, where C represents electric charge in coulomb, and A represents current strength
Dependence of electrical resistance : The electrical resistance of an electronic conductor is linearly proportional to its length (l) and inversely proportional to its cross section area a.
R ∝ l, R ∝ 1/a
∴ R = ρ x l/a
where the proportionality constant ρ is called specific resistance. IUPAC recommends the term resistivity for specific resistance.
∴ Resistivity of the conductor is the resistance of conductor of unit length and unit cross sectional area.
∴ ρ = R x a/l (..Ω x m2/m = Ωm) It has SI units, ohm m and C.G.S. units, ohm cm
Conductivity (k) :
Conductivity is the electrical conductance of a conductor of unit length and unit area of cross section.
The reciprocal of specific resistance or resistivity is called specific conductance or conductivity.
If ρ is the resistivity then,
Conductivity = 1/resistivity = 1/ρ
Conductivity is denoted by k (kappa), where
It is the conductance of a conductor that is 1 m in length and 1 m2 in cross section area in SI units. (In C.G.S. units, it is the resistance of a conductor that is 1 cm in length and 1 cm2 in cross section area.)
It is the conductance of a conductor of volume 1 m3 or in C.G.S. units, the volume of 1 cm3.
Units of specific conductance or conductivity :
If ρ is a resistivity and k is conductivity or specific conductance, then
k = 1/ρ and ρ = R x a/l
∴ k = \(\frac{1}{R}×\frac{l}{a}\) ..... \(\frac{1}{Ω}×\frac{m}{m^2}=\frac{1}{Ωm}\)
In SI units the units of k are ohm−1 m−1 or S m−1 (where S is simense)
In C.G.S. system, the units of k are ohm−1 cm−1 or S cm−1

| Know This :
Use of alternating current in the measurement of conductivity of the solution : If direct Current (D.C.) by battery is used, there will be electrolysis and the concentration of the solution is changed. Hence alternating current (A.C.) with high frequency is used. |
Molar conductivity (∧) :
Molar conductivity : It is defined as a conductance of a volume of the solution containing ions from one mole of an electrolyte when placed between two parallel plate electrodes 1 cm apart and of large area, sufficient to accommodate the whole solution between them, at constant temperature. It is denoted by Λm.
Thus, the significance of molar conductivity is the conductance due to ions from one mole of an electrolyte.
The molar conductivity of an electrolytic solution is the electrolytic conductivity, k, divided by its molar concentration c.
∧ = k/c
SI units of k are S m−1 and that of c are mol m−3. Hence SI units of ∧ are
S m2 mol−1. Common units employed for molar conductivity are Ω−1 cm2 mol−1.
Remember : Conductivity is electrical conductance due to all the ions in 1 cm3 of given solution. Molar conductivity is the electrical conductance due to the ions obtained from 1 mole of an electrolyte in a given volume of solution.
Relation between conductivity (k) and molar conductivity (Λm) :
Conductivity or specific conductance (k) is the conductance of 1 cm3 of the solution in C.G.S. units, while molar conductivity is the conductance of a solution containing one mole of an electrolyte.
Consider C molar solution, i.e., C moles of an electrolyte present in 1 litre or 1000 cm3 of the solution.
‘.’ C moles of an electrolyte are present in in 1000 cm3 solution
∴ 1 mole of an electrolyte is present in 1000/C cm3 solution.
Now,
‘.’ Conductance of 1 cm3 of this solution is k,
∴ Conductance of \(\frac{1000}{C}\) cm3 of the solution is \(\frac{k×1000}{C}\)
This represents molar conductivity, Λm.
∴ Λm = Ω−1 cm2 mol−1 (in C.G.S. units)
In SI Units :
Consider C molar solution, i.e., C moles of an electrolyte present in 1 m3 of the solution.
‘.’ C moles of an electrolyte are present in in 1m3 solution
∴ 1 mole of an electrolyte is present in 1/C m3 solution.
Now,
‘.’ Conductance of 1 m3 of this solution is k,
∴ Conductance of 1000/C cm3 of the solution is
This represents molar conductivity, Λm.
∴ Λm = \(\frac{k}{C}\) Ω−1 m2 mol−1 (in SI unit)
Effect of dilution of solution on conductivity :
(i) Variation of conductivity:
- A solution's conductance is caused by the presence of ions in the solution. The higher the ion concentration, the higher the solution's conductance.
- Conductivity, also known as specific conductance, is the conductance of an electrolytic solution per unit volume (1 cm3).
- The conductivity of an electrolytic solution always decreases as the concentration of the electrolyte or the dilution of the solution decreases.
- On dilution, the concentration of the solution decreases, ‘hence the number of (current carrying) ions per unit volume decreases. Therefore the conductivity of the solution decreases, with the decrease concentration or increase in dilution.
(ii) Variation of molar conductivity :
- It is to be noted here that, molar conductivity increases with dilution.
- The molar conductivity is the electrical conductance of 1 mole of an electrolyte in a given volume of solution. The increasing number of ions produced in solution by 1 mole of the electrolyte lead to increased molar conductivity.
Variation of molar conductivity with concentration :
Variation of molar conductivity with concentration for strong and weak electrolytes :
- As an electrolytic solution's dilution (or concentration) increases, so does the dissociation of the electrolyte, and thus the total number of ions, and thus the molar conductivity.
- The increase in molar conductivity with increase in dilution or decrease in concentration is different for strong and weak electrolytes.
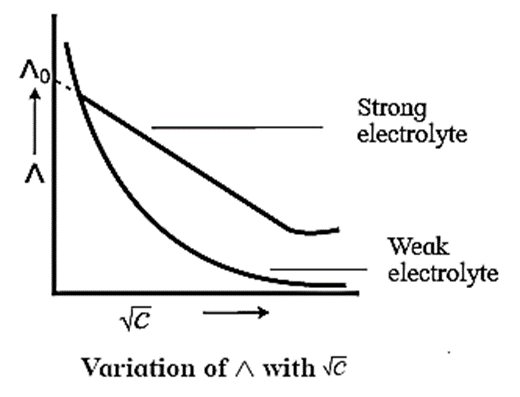
- On dilution, the molar conductivity of strong electrolytes increases rapidly and approaches to a maximum limiting value at infinite dilution or zero concentration and represented as Λ∞ or Λ0 or Λm0. In case of weak electrolytes which dissociate less as compared to strong electrolytes, the molar conductivity is low and increases slowly in high concentration region, but increases rapidly at low concentration or high dilution. This is because the extent of dissociation increases with dilution rapidly.
- Λ0 values for strong electrolytes can be obtained by extrapolating the linear graph to zero concentration (or infinite dilution). However Λ0 for the weak electrolytes cannot be obtained by this method, since the graph increases exponentially at very high dilution and does not intersect Λm axis at zero concentration.
Q. Why has the molar conductance of an electrolyte the maximum value at infinite dilution ?
Therefore the molar conductance at infinite dilute (Λ0) for a given electrolyte has the highest or limiting value. It is always constant for the given electrolyte at constant temperature.
Kohlrausch law of independent migration of ions :
The law states that at infinite dilution each ion migrates independent of co-ion and contributes to total molar conductivity of an electrolyte irrespective of the nature of other ion to which it is associated.
Explanation : Both the ions, cation and anion of the electrolyte make a definite contribution to the molar conductivity of the electrolyte at infinite dilution or zero concentration (Λ0).
If λ0+ and λ0− are the molar ionic conductivities of cation and anion respectively at infinite dilution, then
Λ0 = λ0+ + λ0−
This is known as Kohlrausch’s law of independent migration of ions.
For an electrolyte, Bx Ay giving x number of cations and y number of anions,
Λ0 = xλ0+ + yλ0−
Applications of Kohlrausch’s law :
With this law, the molar conductivity of a strong electrolyte at zero concentration can be determined. For example,
Λ0(KCl) = λ0K+ + λ0Cl−
Λ0 values of weak electrolyte with those of strong electrolytes can be obtained. For example,
Λ0(CH3COOH) = Λ0(HCl) + Λ0(CH3COONa) − Λ0(NaCl) = (λ0H+ + λ0Cl−)+( λ0CH3COOH− + λ0Na+)−( λ0Na+ + λ0Cl−)
Mathematical expression of molar conductivity of the given solution at infinite dilution :
Kohlrausch’s law of independent migration of ions is represented as
Λ0 = λ0+ + λ0−
where Λ0 is the molar conductivity of the electrolyte at infinite dilution or zero concentration while λ0+ and λ0−are the molar ionic conductivities of cation and anion respectively at infinite dilution.
Molar conductivity and degree of dissociation of weak electrolytes :
At zero concentration or at infinite dilution, the molar conductivity has a maximum value denoted by Λ0.
This is due to complete dissociation of the weak electrolyte making all the ions available from one mole of the electrolyte to carry electricity at zero concentration.
If at is the degree of dissociation, then
α = \(\frac{\text{Molar conductivity at given concentration}}{\text{Molar conductivity at zero concentration}}=\frac{Λ_m}{Λ_0}\)
At zero concentration, Λm = Λ0, hence
α = \(\frac{Λ_m}{Λ_0}=\frac{Λ_0}{Λ_0}=1\)
This suggests that at zero concentration or infinite dilution, the electrolyte is completely (100%) dissociated.
Q. Obtain the expression for dissociation constant in terms of Λc and Λ0 using Ostwald’s dilution law.
Ans. Consider a solution of a weak electrolyte, BA having concentration C mol dm−3. If α is the degree of dissociation, then by Ostwald’s theory of weak electrolytes, BA(aq) ⇌ B+(aq) + A−(aq) C(1 − α) Cα C α mol dm−3. If K is the dissociation constant of the weak electrolyte, then by Ostwald’s dilution law, K = \(\frac{α^2C}{1-α}\) If Λm is the molar conductivity of the electrolyte BA at the concentration C and Λ0 is the molar conductivity at zero concentration or infinite dilution, then α = \(\frac{Λ_m}{Λ_0}\) K = \(\frac{(\frac{Λ_m}{Λ_0})^2C}{1-\frac{Λ_m}{Λ_0}}\) = \(\frac{Λ_m^2}{Λ_0^2}×\frac{1}{(\frac{Λ_0-Λ_m}{Λ_0})}×C\) = \(\frac{Λ_m^2C}{Λ_0(Λ_0-Λ_m)}\) Hence by measuring Am at the concentration C and knowing Λ0 the dissociation constant can be calculated. If λ0+ and λ0− are the ionic conductivities, then by Kohlrauschs law, Λ0 = λ0+ + λ0−
Relation between molar conductivity and molar ionic conductivities of electrolytes - examples:
If Λ0 is molar conductivity of an electrolyte at infinite dilution and λ0+ and λ0− are molar ionic conductivities then,
(i) KBr : Λ0KBr = λ0K+ + λ0BR-
(ii) Na2SO4 : Λ0KBr = 2λ0Na+ + λ0SO42+
(c) AlCl3 : Λ0KBr = λ0Al3+ + 3λ0Cl-
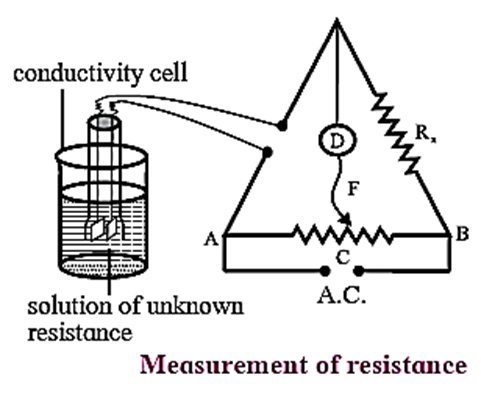
Measurement of conductivity : The conductivity of a solution can be determined from the resistance measurements by Wheatstone bridge.
Conductivity Cell : The conductivity cell consists of a glass tube with two platinum plates coated with a thin layer of finely divided platinium black. This is achieved by the electrolysis of solution of chloroplatinic acid. The cell is dipped in a solution whose resistance is to be measured as shown in Fig
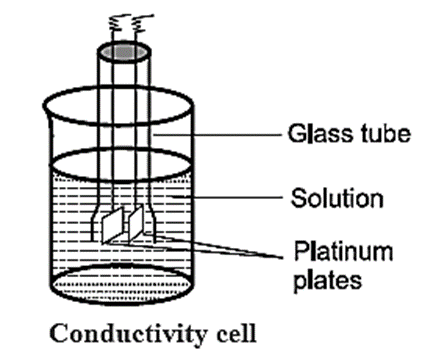
The determination of conductivity consists of three steps :
Step I : Determination of cell constant of the conductivity cell : KCl solution (0.01 M) whose conductivity is accurately known (k = 0.00141 Ω−1cm−1) is taken in a beaker and the conductivity cell is dipped. The two electrodes of the cell are connected to one arm while the variable known resistance (R) is placed in another arm of Wheatstone bridge. A current detector ‘D’ which is a head phone or a magic eye is used. F is the sliding jockey (contact) that slides on the arm AB which is a wire of uniform cross section. A source of A.C. power (alternating power) is used to avoid electrolysis of the solution. By sliding the jockey on wire AB, a balance point (null point) is obtained at C. Let AC and BC be the lengths of wire. If Rsolution is the resistance of KCl solution and RX is the known resistance then by Wheatstone’s bridge principle, \(\frac{R_{solution}}{BC}=\frac{R_x}{AC}\) ∴ Rsolution = \(BC×\frac{R_x}{AC}\) Then the cell constant ‘b’ of the conductivity cell is obtained by, b = kKCl x Rsolution Step II : Determination of conductivity of the given solution : KCl solution is replaced by the given electrolytic solution and its resistance (RS) is measured by Wheatstone bridge method by similar manner by obtaining a null point at D. The conductivity (k) of the given solution is, k = \(\frac{\text{cell constant}}{R_s}=\frac{b}{R_s}\) Step III : Calculation of molar conductivity : The molar conductivity (Λm) is given by, Λm = \(\frac{k}{C}\) or \((Λ_m = \frac{1000×k}{C})\) Since the concentration of the solution is known Λm can be calculated.
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-4- Chemical Thermodynamics – Online Notes
Next Chapter : Chapter-6-Chemical Kinetics – Online Notes
We reply to valid query.