Magnetism
Maharashtra Board-Class-11-Science-Physics-Chapter-12
Solutions
Question 1. Choose the correct option.
(i) Let r be the distance of a point on the axis of a bar magnet from its center. The magnetic field at r is always proportional to
(A) 1/r2
(B) 1/r3
(C) 1/r
(D) not necessarily 1/r3 at all points
(D) not necessarily 1/r3 at all points
(ii) Magnetic meridian is the plane
(A) perpendicular to the magnetic axis of Earth
(B) perpendicular to geographic axis of Earth
(C) passing through the magnetic axis of Earth
(D) passing through the geographic axis Earth
(C) passing through the magnetic axis of Earth
(iii) The horizontal and vertical component of magnetic field of Earth are same at some place on the surface of Earth. The magnetic dip angle at this place will be
(A) 30o
(B) 45o
(C) 0o
(D) 90o
(B) 45o
(iv) Inside a bar magnet, the magnetic field lines
(A) are not present
(B) are parallel to the cross sectional area of the magnet
(C) are in the direction from N pole to S pole
(D) are in the direction from S pole to N pole
(D) are in the direction from S pole to N pole
(v) A place where the vertical components of Earth's magnetic field is zero has the angle of dip equal to
(A) 0o
(B) 45 o
(C) 60 o
(D) 90 o
(A) 0o
(vi) A place where the horizontal component of Earth's magnetic field is zero lies at
(A) geographic equator
(B) geomagnetic equator
(C) one of the geographic poles
(D) one of the geomagnetic poles
(D) one of the geomagnetic poles
(vii) A magnetic needle kept nonparallel to the magnetic field in a nonuniform magnetic field experiences
(A) a force but not a torque
(B) a torque but not a force
(C) both a force and a torque
(D) neither force nor a torque
(C) both a force and a torque
Question 2. Answer the following questions in brief.
(i) What happens if a bar magnet is cut into two pieces transverse to its length/ along its length?
- A bar magnet can be cut into two halves, exposing two new faces with opposite poles. The magnetic dipole moment of each piece is half that of the original magnet.
- If cut transversely, the new exposed poles have the same pole strengths as the original but have half the magnetic length.
- If cut along its length, the new exposed poles have half the pole strengths as the original but have the same magnetic length.
(ii) What could be the equation for Gauss' law of magnetism, if a monopole of pole strength p is enclosed by a surface?
Gauss‘ law in magnetism would be analogous to that in electrostatics : The net magnetic flux through a surface enclosing a monopole of pole strength p would be equal to the product μ0p, where μ0 is the permeability of free space.
\(\oint \limits_{s} \vec{B}.\vec{dS}\) = μ0p
where the integration is over the closed surface S enclosing the magnetic monopole.
Question 3. Answer the following questions in detail.
(i) Explain the Gauss' law for magnetic fields.
Gauss’ law in magnetism : The net magnetic flux Φm through a closed surface of arbitrary shape is zero.
In integral form, Φm = \(\oint \limits_{s} \vec{B}.\vec{dS}\) = 0
where the integration is over a closed surface S.
Explanation : Below figure schematically shows the magnetic field lines of a bar magnet and a current—carrying solenoid, and the electric field lines of an electric dipole. The dotted curves S1 and S2 represent Gaussian surfaces.
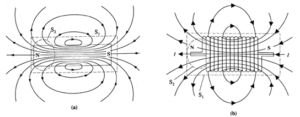
In Figs. (a) and (b), the number of magnetic field lines entering each of the surfaces S1 and S2 are equal to the number of lines leaving the respective surfaces. That is, the net flux Φm through them is zero. Although S2 appears to enclose the north pole, Φm = 0 means that there is no magnetic charge there.
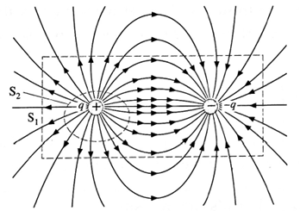
For an electrostatic case, however, Gauss’ law states that the net electric flux through a closed surface S is Φe = \(\oint \limits_{s} \vec{E}.\vec{dS}=\frac{∑q}{ε_0}\), where ∑q is the net electric charge enclosed by S.
In below Fig. Φe =0 through S1 and ∑q is also zero, while there is a net outward flux through S2 and ∑q = + q, both cases consistent with Gauss’ law and the fact that an isolated electric charge exists.
Thus, by Gauss’ law in magnetism,
- magnetic monopoles do not exist — magnetic field is dipolar in character.
- net magnetic flux through any volume is always zero.
(ii) What is a geographic meridian. How does the declination vary with latitude? Where is it minimum?
- Geographic meridian : The vertical plane at a place through the geographic North and South Poles (i.e., containing the geographic axis) is called the geographic meridian at that place.
- Magnetic declination does not depend on latitude. The lines of flux are pretty random.
(iii) Define the Angle of Dip. What happens to angle of dip as we move towards magnetic pole from magnetic equator?
- Angle of Dip (or inclination) : At a place on the Earth's surface, the magnetic induction of the Earth \(\vec{B}\) is, in general, inclined to the surface. A dip needle placed with its plane in the magnetic meridian points in the direction of at that place. The angle which a dip needle makes with the horizontal is the angle between \(\vec{B}\) and the horizontal. This angle is called the dip or inclination, δ at the place.
- On the magnetic equator, dip angle = 0°. At the north and south magnetic poles, the dip angle is 90° and 270° degrees.
Question 4. Solve the following Problems.
(i) A magnetic pole of bar magnet with pole strength of 100 A.m is 20 cm away from the centre of a bar magnet. Bar magnet has pole strength of 200 A.m and has a length 5 cm. If the magnetic pole is on the axis of the bar magnet, find the force on the magnetic pole.
Given : qm = 100 A.m, d = 20 cm = 0.2 m, 2l = 5 x 10−2 m, qmB =200 A.m, \(\frac{μ_0}{4π}\) = 10−7 T.m/A
Dipole moment of the bar magnet,
m = qmB(2l) = (200)( 5 x 10−2) = 10 A·m2
The axial field of the short bar magnet,
Baxis = \(\frac{μ_0}{4π}.\frac{2m}{d^3}\) = (10−7)\((\frac{2(10)}{0.2^3})\) = 2.5 x 10−4 T
∴ The force on the magnetic pole,
F = qm x Baxis = (100) (2.5 x 10−4) = 2.5 x 10−2 N = 25 mN
(ii) A magnet makes an angle of 45o with the horizontal in a plane making an angle of 30o with the magnetic meridian. Find the true value of the dip angle at the place.
Here, the dip needle is placed in a plane that makes an angle of 30° with the magnetic meridian. Then, as shown in the figure, the dip needle lies in the plane OSTR which makes an angle θ = 30° with the plane OPQR which is in the magnetic meridian. In the figure, \(\vec{B}=\vec{B}_h+\vec{B}_v\) is the Earth's magnetic field at the place and \(\vec{B}_1\) is the component of \(\vec{B}\) along the dip needle.
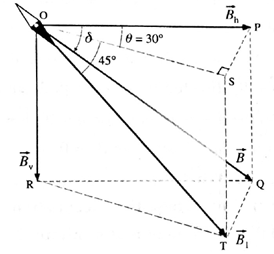
Bv =ST =OT sin ∠ SOT = B1 sin 45°
Also, OS = OP cos 0
∴ OT cos 45° = OP cos θ
∴ B1 cos 45° = Bh cos 30°
∴ Bh = B1 cos 45° / cos 30°
∴ The true dip angle is given by
tan δ = \(\frac{B_v}{B_h}\) = \(\frac{B_1\,sin\,45°}{B_1\,cos\,45°/cos\,30°}\) = tan 45° cos 30° = (1)\((\frac{\sqrt{3}}{2})\)
∴ δ = tan-1\((\frac{\sqrt{3}}{2})\) = 40°54'
(iii) Two small and similar bar magnets have magnetic dipole moment of 1.0 A.m2 each. They are kept in a plane in such a way that their axes are perpendicular to each other. A line drawn through the axis of one magnet passes through the center of other magnet. If the distance between their centers is 2 m, find the magnitude of magnetic field at the mid point of the line joining their centers.
Given : m1 = m2 = 1 A.m2, distance between their centres = 2 m, \(\frac{μ_0}{4π}\) = 10−7 T.m/A
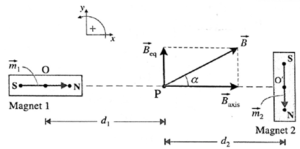
Point P lies on the axis of magnet 1 and on the equator of magnet 2, equidistant from both (Fig.). Since OO'= 2 m, d1 = d2 = 1m
Orienting the magnetic moments and as shown without loss of generality, the axial field of magnet 1 at P is
\(\vec{B}_1\) = \(\frac{μ_0}{4π}.\frac{2m_1}{d_1^3}\)
= (10−7)\((\frac{2(1)}{1^3})\) = (2 x 10−7 T)\(\hat{i}\)
and the equatorial field of magnet 2 at P is,
\(\vec{B}_2\) = \(\frac{μ_0}{4π}.\frac{-\vec{m}_1}{d_2^3}\)
= (10−7)\((\frac{1}{1^3})\) = (10−7 T)\(\hat{j}\)
∴ The net magnetic induction at P,
\(\vec{B}=\vec{B}_1+\vec{B}_2\) = \((2\hat{i}+\hat{j})\) x 10−7 T
∴ The magnitude of the net magnetic induction at P,
B = |(\vec{B}\)| = 10−7 x \(\sqrt{2^2+1^2}\) = \(\sqrt{5}\) x 10−7 T
tan ∝ = B2/B1 = 1/2
∴ The angle made by with = ∝ = tan−1 \((\frac{1}{2})\) = 26°36’
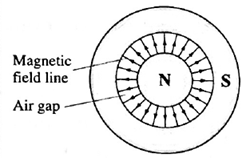
(iv) A circular magnet is made with its north pole at the centre, separated from the surrounding circular south pole by an air a gap. Draw the magnetic field lines in the gap. [The magnet is hypothetical magnet]. Draw a diagram to illustrate the magnetic lines of force between the south poles of two such magnets.
(i) For south poles of such circular magnets facing each other:
(ii) For south poles of bar magnets facing each other:
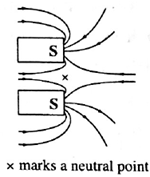
Note : The question is wrong as isolated magnetic monopoles are not observed.
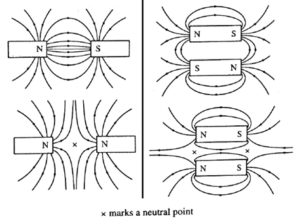
(v) Two bar magnets are placed on a straight line with their north poles facing each other on a horizontal surface. Draw magnetic lines around them. Mark the position of any neutral points (points where there is no resultant magnetic field) on your diagram.
The magnetic lines of force between two magnets will depend on their relative positions. Considering the magnets to be placed one beside the other as shown in the figure, the magnetic lines of force will be as shown.
In Fig. neutral point(s), where the resultant magnetic field is zero, are marked with a cross.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 11: Electric Current Through Conductors – Online Solutions
Next Chapter : Chapter 13: Electromagnetic Waves and Communication System – Online Solutions
We reply to valid query.