Notes Part-2
Topics to be Learn : Part-2
|
Quantum mechanical model of atom :
Quantum machanics, developed in 1926 by Werner Heisenberg and Erwin Schrodinger based on uncertainty principle and wave motion, respectively.
An atomic model developed on the basis of quantum mechanics is called quantum mechanical model. Quantum mechanics is a theoretical science that deals with microscopic particles that have wave like and particle like properties.
A fundamental equation of quantum mechanics called Schrodinger equation is represented as, \(\cap{H}Ψ\) = E Ψ where \(\cap{H}\) is a mathematical operator called Hamiltonian, Ψ is a wave function and E is the total energy of the system.
Schrodinger equation : When Schrodinger equation is solved for hydrogen atom, the possible values of energy (E) that the electron may have along with the corresponding wave function (ψ) are obtained.
As a natural consequence of solving this equation, a set of three quantum numbers characteristic of the quantized energy levels and the corresponding wave functions are obtained. These are :
- Principal quantum number (n),
- azimuthal quantum number (l) and
- magnetic quantum number (ml).
Splitting of spectral lines in multi-electron atomic emission spectra could not be explained through above model. These were explained by George Uhlenbeck and Samuel Goudsmit (1925) who proposed the presence of the fourth quantum number called electron spin quantum number, ms.
Principal quantum number (n) : This describes the orbit or shell of an atom to which the electron belongs. It is represented by ‘n’ which has integral values. The energy of an electron depends on the value of n.
| Principal quantum number n | Shell symbol | Allowed number of orbitals n2 | Size of shell |
| 1 | K | 1 |  |
| 2 | L | 4 | |
| 3 | M | 9 | |
| 4 | N | 16 |
Azimuthal quantum number (l) : This represents the subsidiary quantum number or the subshell of the orbit to which the electron belongs. It is denoted by l. It is also called as secondary, subsidiary, orbital or angular momentum quantum number. It defines the shape of the orbital and the angular momentum of the electron. The value of l depends on principal quantum number n. It has positive values between 0 to (n — 1) :
| l | 0 | 1 | 2 | 3 |
| subshell | s | p | d | f |
This explains the significance of azimuthal quantum number.
Mgnetic orbital quantum number (ml) : This gives the information about the relative spatial orientation of the orbitals in a given subshell defined by ’l’. For any subshell total orientations possible are (2l + 1) which range through :
ml = −l, − (l−1),...O .... ..(l−1),l
The total values are 2l + 1.
The sum of orbitals in a subshell gives the total number of orbitals in a shell and is given by n2.
| Value of l | orbital | ml values |
| 0 | s | 0 |
| 1 | p | −1, 0, +1 |
| 2 | d | −2,−1, 0, +1, +2 |
| 3 | f | −3,−2,−1, 0, +1, +2, +3 |
Electron spin quantum number, (ms) : An electron spins around its axis clockwise or anticlockwise and imparts spin angular momentum to it. The two spin states are represented as ↑ or ↓ with ms values \(+\frac{1}{2}\) or \(-\frac{1}{2}\) respectively.
An orbital can accommodate maximum two electrons and they must have opposite spins.
Subshells :
There are four subshells as follows :
(1) s-subshell : For this subshell l= 0, ml = 0. This implies that s-subshell has only one orbital i.e., s-orbital.
(2) p-Subshell : For this subshell, l = 1, m = +1, 0, −1. Hence p-subshell has three orbitals represented as px, py and pz and they are respectively oriented along x, y and z axes. Therefore p-orbitals have three-fold degeneracy.
(3) d-subshell : For this subshell, l =2, m = +2, +1, 0, −1, −2. Hence, d-subshell has five orbitals with five different orientations. They are designated as dxy, dyz dxz, which are planar orbitals and , are axial orbitals. Therefore d-orbitals have five-fold degeneracy.
(4) f-subshell : For this subshell, l = 3, m = +3, + 2, + 1, 0, — 1, — 2, —3. Hence f-subshell has seven orbitals with seven orientations in space.
They are designated as Therefore f-orbitals have seven fold degeneracy.
Distribution of orbitals in shells and subshells : Below Table shows orbitals in the first four shells with the three quantum numbers for each orbital.
Q. How many orbitals make the N shell? What is the subshell wise distribution of orbitals in the N shell?
Ans : For N shell principal quantum number n =4. Hence total number of orbitals in N shell = n2 = 42 = 16. The total number of subshells in N shell = n = 4. The four subshells with their azimuthal quantum numbers and the constituent orbital number are as shown below :
Azimuthal quantum number l
Symbol of subshell
Number of orbitals 2l + 1
l = 0
s
(2 x 0) + 1 = 1
l =1
p
(2 x 1) + 1 = 3
l = 2
d
(2 x 2) + 1 = 5
l = 3
f
(2 x 3) + 1 = 7
Shapes of atomic orbitals : Orbital : The three dimensional region in the space around the nucleus of an atom in which the probability of finding the electron is maximum is called orbital. Shapes of 1s, 2s orbitals : Figure shows the boundary surface diagram of atomic orbitals 1s and 2s, which are spherical in shape. Here, a boundary surface is drawn in space for an orbital such that the value of probability density Ψ2 is constant and encloses a region where the probability of finding electron is typically more than 90%. Such a boundary surface diagram is a good representation of shape of an orbital. p-orbital : d-orbital : The shapes of 3d, 4d, 5d ..... orbitals are similar but their respective size and energies are large or they are said to be more diffused.
Energies of orbitals :
The energy of an electron in the hydrogen atom or hydrogen like species is determined by the principal quantum number alone. This is because the only interaction in these species is attraction between the electron and nucleus.
Degenerate orbitals : The orbitals with the same energy and the corresponding wave functions being different are called degenerate orbitals. In hydrogen atom 2s and 2p are degenerate orbitals.
n + l rule : The energy of an electron in a multi-electron atom, depends both on the principal quantum number, n, and the azimuthal quantum number, l. The lower the sum (n + 1) for an orbital, the lower is its energy. If two orbitals have the same (n +1) values then orbital with the lower value of n is of lower energy. This is called the (n +1) rule. From the (n +1) rule the increasing order of energy of orbitals in multi-electron atoms can be written as : 1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s<4f<5d<6p<7s .......
Ground state of an atom : It is a state of the lowest total electronic energy. For example, of hydrogen atom it is 1s state.
Aufbau principle : ‘
Aufbau is a German word which means building up. This principle explains the sequence of filling up of orbitals with electrons.
Aufbau principle : It states that in the ground state of an atom, the orbitals are filled with electrons in order of the increasing energies.
The orbitals are filled in order of increasing value of (n + l). For example, 4s-orbital
(n + l = 4 + 0 = 4) is filled prior to 3d-orbital (n + l = 3 + 2 = 5).
Among two orbitals having same (n + l) value, that orbital with lower value of n will be filled first. For example, 3d-orbital (n + l = 3 + 2 = 5) is filled prior to 4p-orbital (n + l = 4 + 1 = 5).
The increasing order of energy of different orbitals is as follows :
1s<2s<2p<3s<3p<4sz<3d<4p<5s<4d<5p<6s<4f<5d<6p<7s<5f<6d
Pauli exclusion principle : The capacity of an orbital to accommodate electrons is decided by Pauli exclusion principle.
Statement of Pauli’s principle : No two electrons in an atom can have all the four quantum numbers, (n, l, m and s) same.
OR
Only two electrons may exist in the given orbital having three quantum numbers same but fourth quantum number being different with opposite spins.
This principle describes the capacity of a sub-shell or orbital to accommodate maximum number of electrons.
Consider helium atom, which has two electrons. The four quantum numbers of two electrons in He atom will be,
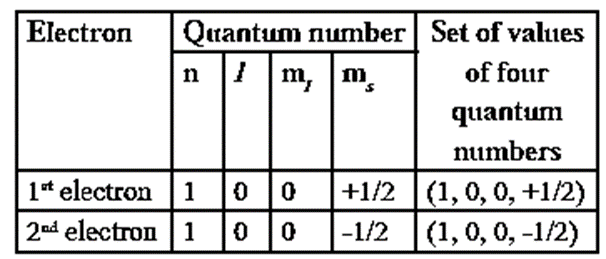
This principle is illustrated with helium atom He (Z = 2). Its electronic configuration is 1s2 as
Hund’s rule of maximum multiplicity :
Statement of Hund’s rule of maximum multiplicty : It states that pairing of electrons in the orbitals belonging to the same subshell does not occur unless each orbital belonging to that subshell has accommodated one electron each.
- Consider filling of p-subshell which has three degenerated orbitals namely
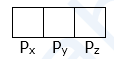
After filling three electrons, one in each with same spins, the next electrons enter with pairing
It observed that half filled and completely filled set of degenerate orbitals have extra stability.
Electronic configuration of atoms and its representation :
Electronic configuration of an atom is the distribution of its electrons in orbitals.
The electronic configuration can be written by applying the aufbau principle.
There are two methods of representing electronic configuration:
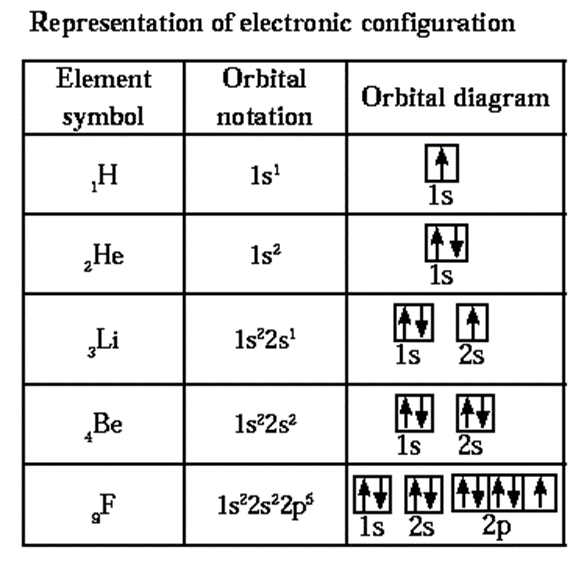
(i) Orbital notation: nsa npb ndc..........
For example for boron atom 5B 1s2, 2s2, 2p1.
(ii) Orbital diagram :
Condensed orbital notation of electronic configuration :
- The orbital notation of electronic configuration of an element with high atomic number can be condensed by dividing it into two parts.
- The electronic configuration of the preceding inert gas is a part of the electronic configuration of every element.
- In the condensed orbital notation inert gas is mentioned by writing the symbol of that inert gas in a square bracket and outside remaining configuration is written immediately after the bracket.
For example,
Consider an element 19K. Its electronic configuration is 1s2 2s2 2p6 3s2 3p6 4s1
The preceding inert element Argon has electronic configuration, 18Ar 1s2 2s2 2p6 3s2 3p6
Hence the condensed orbital notation for potassium is 19K : [Ar] 4s1
Orbital diagram method :
In the orbital diagram method each orbital in a subshell is represented by a box and the electron represented by an arrow (↑for up spin and ↓for low spin) placed in the respective boxes.
Electronic configurations of Cu and Cr : (i) Copper (Cu) : Copper (29Cu) has electronic configuration. 29Cu (Expected) : 1s2, 2s2, 2p6, 3s2, 3p6, 3d9, 4s2 (Observed) : 1s2, 2s2, 2p6, 3s2, 3p6, 3d10, 4s1 Explanation : (ii) Chromium (Cr) : Chromium (24Cr) has electronic configuration, 24Cr (Expected) : 1s2, 2s2, 2p6, 3s2, 3p6, 3d4, 4s2 (Observed) : 1s2, 2s2, 2p6, 3s2, 3p6, 3d5, 4s1 Explanation :
Isoelectronic species : Atoms and ions having the same number of electrons are isoelectronic species.
Example :
Consider K+ formed by removal of one electron from K atom. Which has 19 electrons (Z = 19). Therefore K+ has 18 electrons.
Species such as Ar, Ca2+ containing 18 electrons are isoelectronic with K+ .
Electronic configuration of all these species with 18 electrons is 1s2, 2s2, 2p6, 3s2, 3p6.
| Species | K→ K+ + e− | Ar, Ca2+ |
| Number of electrons | 19 18 | 18 18 |
Electronic configuration of the first fifteen elements
Energy of an electron (E) = eV Wave number of a spectral line, \(\bar{v}=\frac{1}{λ}=R(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}})\) Rydberg’s constant = R = 1.09677 x 107 m−1 Quantum numbers of an electron : n, l, m1 , m2 For photoelectric effect : hv = hvo + ½ mv2 De Broglie equation : λ = h/mv Heisenberg’s uncertainty principle : Δx x Δp ≥ h/4π Schrodinger’s wave equation : \(\frac{d^2ψ}{dx^2}+\frac{d^2ψ}{dy^2}+\frac{d^2ψ}{dz^2}+\frac{8π^2m}{h^2}(E-V)φ=0\)
Important formulae
We reply to valid query.