Solutions
Practice set 4.1
Question 1.
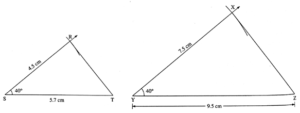
Δ ABC ~ Δ LMN. In Δ ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct Δ ABC and Δ LMN such that \(\frac{BC}{MN}=\frac{5}{4}\).
For Δ ABC, the lengths of three sides are known.
∴ Δ ABC can be constructed.
Δ ABC ~ Δ LMN
∴ \(\frac{AB}{LM}=\frac{BC}{MN}=\frac{AC}{LN}\) ….. (Corresponding sides of similar triangles are in proportion)
∴ \(\frac{5.5}{LM}=\frac{6}{MN}=\frac{4.5}{LN}=\frac{5}{4}\)
To find LM :
\(\frac{5.5}{LM}=\frac{5}{4}\)
∴ LM = \(\frac{5.5×4}{5}\) = 1.1 × 4 = 4.4 cm
To find MN :
\(\frac{6}{MN}=\frac{5}{4}\)
∴ MN =\(\frac{6×4}{5}=\frac{24}{5}\) = 4.8 cm
To find LN :
\(\frac{4.5}{LN}=\frac{5}{4}\)
∴ LN = \(\frac{4.5×4}{5}=\frac{18}{5}\) = 3.6 cm
Now, construct Δ LMN such that LM = 4.4 cm, MN = 4.8 cm and NL = 3.6 cm.
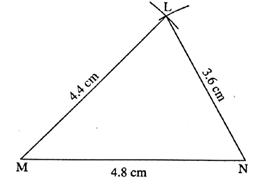
Question 2.
Δ PQR ~ Δ LTR. In Δ PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct Δ PQR and Δ LTR, such that \(\frac{PQ}{LT}=\frac{3}{4}\).
As shown in fig, let the points R, P, L and RQT be collinear.
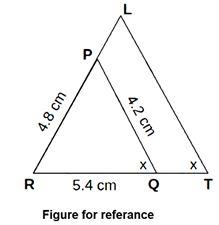
Δ PQR ~ Δ LTR …(Given)
∴ ∠ PRQ = ∠ LRT ... [Corresponding angles of similar triangles]
∴ \(\frac{RP}{RL}=\frac{RQ}{RT}=\frac{PQ}{LT}=\frac{3}{4}\)
∴ sides of Δ LTR are longer than corresponding sides of Δ PQR.
∴ the length of side QR will be equal to 3 parts out of 4 equal parts of side TR.
So, if we construct Δ PQR, point T will be on side RQ, at a distance equal to 4 parts form R.
Now, point L is the point of intersection of ray RP and a line through T, parallel to PQ.
Δ LTR is the required triangle similar to Δ PQR.
Steps of Construction:
(1) Draw Δ PQR such that PQ = 4.2 cm, QR = 5.4 cm and PR = 4.8 cm, choosing QR = 5.4 cm as base.
(2) Draw ray RX making an acute angle with side RQ.
(3) Taking convenient distance on the compass, mark 4 points R1, R2, R3, and R4, such that RR1 = R1R2 = R2R3 = R3R4.
(4) Join R3Q. Draw line parallel to R3Q through R4 to intersects ray RQ at T.
(5) Draw a line parallel to side PQ through T. Name the point of intersection of this line and ray RP as L.
(6) Δ LTR is the required triangle similar to Δ PQR.
Question 3.
Δ RST ~ Δ XYZ. In Δ RST, RS = 4.5 cm, ∠ RST = 40°, ST = 5.7 cm. Construct Δ RST and Δ XYZ, such that \(\frac{RS}{XY}=\frac{3}{5}\).
For Δ RST, the lengths of two sides and included angle are known.
∴ Δ RST can be constructed.
Δ RST ~ Δ XYZ …(Given)
∴ \(\frac{RS}{XY}=\frac{ST}{YZ}=\frac{3}{5}\) ….. (Corresponding sides of similar triangles are in proportion)
∴ \(\frac{4.5}{XY}=\frac{5.7}{YZ}=\frac{3}{5}\)
To find XY :
\(\frac{4.5}{XY}=\frac{3}{5}\)
∴ XY = \(\frac{4.5×5}{3}\) = 7.5 cm
To find YZ :
\(\frac{5.7}{YZ}=\frac{3}{5}\)
∴ YZ = \(\frac{5.7×5}{3}\) = 9.5 cm
∠ RST = ∠ XYZ = 40° ... (Corresponding angles of similar triangles are congruent)
For Δ XYZ, the lengths of two sides and included angle are known.
∴ Δ XYZ can be constructed.
Question 4.
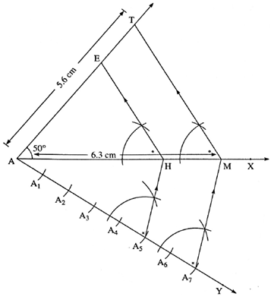
Δ AMT ~ Δ AHE. In Δ AMT, AM = 6.3 cm, ∠ TAM = 50°, AT = 5.6 cm. \(\frac{AM}{AH}=\frac{7}{5}\). Construct Δ AHE.
As shown in the figure,
Let A-H-M as well as points A-E-T be collinear.
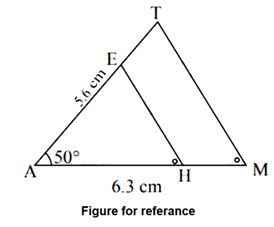
Δ AMT ~ Δ AHE,
∴ ∠ TAM = ∠ EAH ... (Corresponding angles of similar triangles)
∴ \(\frac{AM}{AH}= \frac{AT}{AE}=\frac{TM}{EH}\) ... (i) ..(Corresponding sides of similar triangles)
\(\frac{AM}{AH}=\frac{7}{5}\) … (ii) …(given)
∴ \(\frac{AM}{AH}= \frac{AT}{AE}=\frac{TM}{EH}=\frac{7}{5}\) ….from (i) and (ii)
∴ sides of Δ AHE are smaller than sides of Δ AMT.
∴ If seg AH will be equal to 5 parts out of 7 equal parts of side AM.
So, if we construct Δ AMT, point H will be on side AM, at a distance equal to 5 parts from A.
Now, point E is the point of intersection of ray AT and a line through H, parallel to MT.
Δ AHE is the required triangle similar to Δ AMT.
Steps of Construction:
(1) Draw Δ AMT such that AM = 6.3 cm, ∠ TAM = 50°, AT = 5.6 cm.
(2) Draw ray AY making an acute angle with side AM.
(3) Taking convenient distance on the compass, mark 7 points A1, A2, A3, A4, A5, A6 and A7, such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7.
(4) Join A7M. Draw line parallel to A7M through A5 to intersects seg AM at H.
(5) Draw a line parallel to side TM through H. Name the point of intersection of this line and seg AT as E.
Δ AHE is the required triangle similar to Δ AMT.
Practice set 4.1
Question 1.
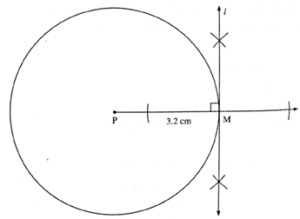
Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Steps of Construction:
(1) Draw a circle with centre P and radius 3.2 cm.
(2) Take any point M on the circle.
(3) Draw ray PM.
(4) Draw line I perpendicular to ray PX through point M.
Question 2.
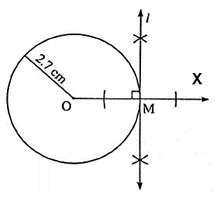
Draw a circle of radius 2.7 cm. Draw a tangent to the circle at any point on it.
Steps of Construction:
(1) Draw a circle with centre O and radius 2.7 cm.
(2) Take any point M on the circle.
(3) Draw ray OX.
(4) Draw line l perpendicular to ray OX through point M.
Question 3.
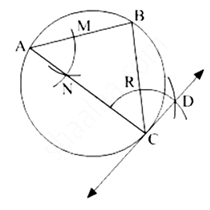
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Steps of Construction:
(1) Draw a circle with radius 3.6 cm. Mark any point C on it.
(2) Draw chord CB and an inscribed ∠ CAB.
(3) With the centre A and any convenient radius draw an arc intersecting the sides of ∠ BAC in points M and N.
(4) Using the same radius and centre C, draw an arc intersecting the chord CB at point R.
(5) Taking the radius equal to d(MN) and centre R, draw an arc intersecting the arc drawn in step 4. Suppose D be the point of intersection of these arcs. Draw line CD.
Here, line CD is the required tangent to the circle.
Question 4.
Draw a circle of radius 3.3 cm Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your obeservation about the tangents.
Steps of Construction:
(1) Draw a circle with centre O with radius 3.3 cm, Mark any point P on it.
(2) Draw chord PQ = 6.6 cm (PQ is the diameter of the circle).
(3) Draw rays OX and OY.
(4) Draw line M perpendicular to ray OX through point P.
(5) Draw line N perpendicular to ray OY through point Q.
Here, line M and line N are the required tangents to the circle at points P and Q, respectively.
It can be observed that the tangents M and N are parallel to each other.
Question 5.
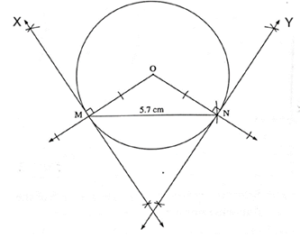
Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. Construct tangents at point M and N to the circle.
Steps of Construction:
seg OM ⊥ line X
seg ON ⊥ linel Y …..[Tangent is perpendicular to radius]
The perpendicular to seg ON and seg OM at points N and M respectively will give the required tangents at N and M.
Question 6.
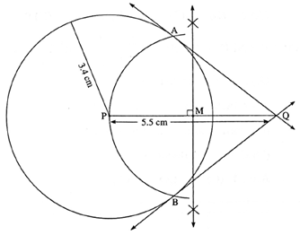
Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Steps of construction :
(1) Draw a circle of radius 3.4 cm.
(2) Take a point Q in the exterior of the circle such that d(P, Q) = 5.5 cm.
(3) Draw seg PQ. Draw perpendicular bisector of seg PQ to get its midpoint M.
(4) Draw an arc with radius PM and centre M.
(5) Mark the points of intersection of the arc with the circle as A and B.
(6) Draw line QA and QB.
Ray QA and QB are the required tangents to the circle from point Q.
Question 7.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Steps of construction :
(1) Draw a circle of radius 4.1 cm.
(2) Take a point P in the exterior of the circle such that d(O, P) = 7.3 cm.
(3) Draw seg OP. Draw perpendicular bisector of seg OP to get its midpoint M.
(4) Draw an arc with radius OM and centre M.
(5) Mark the points of intersection of the arc with the circle as A and B.
(6) Draw line PA and PB.
Ray PA and PB are the required tangents to the circle from point P.
