Motion in a Plane
Maharashtra Board-Class-11-Science-Physics-Chapter-3
Notes-Part-1
|
Topics to be Learn : Part-1
|
Rectilinear Motion:
Motion : Motion is a change in the position of a body with respect to time as measured by an observer in a specific frame of reference.
The motion of objects can be divided in three categories:
- Motion along a straight line, i.e., rectilinear motion,
- Motion in two dimensions, i.e., motion in a plane
- Motion in three dimensions, i.e., motion in space.
A rectilinear motion is a one-dimensional translatory motion.
A particle moving along a curved path in a plane has two-dimensional motion.
A particle moving in space has, in general, three-dimensional motion.
Displacement : The displacement of a particle in a given time interval is defined as its change of position in the elapsed time.
- It is given by the vector drawn from the initial position of the particle, i.e., the position at time t1, to its final position, i.e., the position at a later time t2.
- In rectilinear motion, the displacement is along the line of motion of the particle.
If \(\vec{x_1}\)and \(\vec{x_2}\) are the position vectors of the particle at instants t1 and t2 respectively, then the displacement \(\vec{s}\) of the particle during the time interval
Δt = t2 − t1 is \(Δ\vec{x}\) = \(\vec{x_2}\) − \(\vec{x_1}\)
Characteristics of displacement :
- It is a vector quantity, directed from the initial position of a particle to its final position.
- The magnitude of the displacement is the length of the straight line, i.e., the shortest path length, between the initial and final positions of a particle.
- The magnitude of the displacement is less than or equal to the path length between the initial and final positions of a particle.
- The displacement may be zero, positive or negative.
- It has the dimension of length.
Path length: This is the actual distance travelled by the object during its motion.
- It is a scalar quantity and its dimensions are also that of length.
Average velocity : The average velocity of a particle is the displacement of the particle divided by the time elapsed during which the displacement occurs.
If \(\vec{x_1}\)and \(\vec{x_2}\) are the position vectors of the particle at instants t1 and t2 respectively, then
\(\vec{v_{av}}\)=\(\frac{Displacement}{Time}\)=\(\frac{Δ\vec{x}}{dt}=\frac{x_2-x_1}{t_2-t_1}\)
Instantaneous velocity : The velocity at a given instant is called the instantaneous velocity and is defined as the limiting value of the average velocity as the time interval approaches zero.
\(\vec{v}=\lim_{x→0}\frac{dx}{dt}\)
- Δt —> 0, means Δt is very small or nearly zero; but Δt ≠ 0. For Δt = 0, there is no motion.
- In general, when we say velocity, we mean instantaneous velocity.
Uniform velocity : Velocity is said to be uniform if it remains constant with time both in magnitude and direction. In such a case, the acceleration is zero and the instantaneous velocity equals the average velocity.
Average speed : The average speed is the total distance or path length travelled by a particle divided by the time elapsed during which the motion occurs.
Conditions : In a given time interval, the displacement and average velocity of a particle are both zero if its initial and final positions are the same, i.e.,
- (i) when the particle is at rest or
- (ii) it returns to its initial position.
(1) For a particle at rest, the path length is zero and, hence, the average speed is also zero.
(2) In the second case, the total path length > 0 so that a
Average Speed = \(\frac{\text{Total path length}}{\text{Elapsed time}}\) > 0
(3) Since total path length can be zero (when the particle is at rest) or positive, i.e., never negative, average speed can never be negative.
(4) By definition, in a given time interval,
Average Speed = \(\frac{\text{Total path length}}{\text{Elapsed time}}\)and its
Average velocity = .\(\frac{\text{Displacement}}{\text{Elapsed time}}\)
Since total path length ≥ |displacement|,
∴ average speed ≥ |average velocity|
i.e. the average speed of a body is greater than or equal to the magnitude of its average velocity over a given time interval.
Instantaneous speed: Instantaneous speed is the speed at a given instant. It is the magnitude of the instantaneous velocity.
- So, instantaneous speed is never negative.
- The average speed and instantaneous speed are equal for a motion with uniform velocity, i.e., for a uniform motion in a straight line.
Distinguish between path length and displacement : final positions of the particle.
Path length
Displacement
It is the actual length of the path travelled by a particle during its motion.
It is a directed straight line from the initial to the final position of the particle giving its change of position.
It is greater than or equal to the magnitude of the displacement.
Its magnitude is the shortest path length and hence less than or equal to the path length between the initial and
It may be zero or positive.
It may be zero, positive or negative.
It is a scalar quantity
It is a vector quantity.
| Remember:
For uniform rectilinear motion, i.e., for an object moving with constant velocity along a straight line
For nonuniform rectilinear motion
|
Graphical Study of Motion :
Position-time graph : The position-time graph for a particle is a plot of the position x of the particle with respect to a reference point (origin O) against time t.
Time is the independent variable and plotted on the x-axis. The position of the particle is the dependent variable and is plotted on the y-axis (according to the Cartesian sign convention).
(i) Position-time graphs (x-t graph) for a particle at rest :
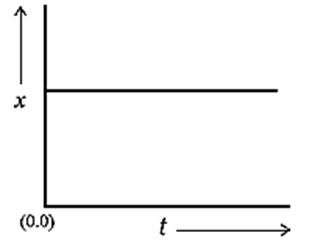
Fig.- Position-time graphs for a particle at rest
The graph x = x0 is a straight line parallel to the time axis which means that the position of the particle is independent of time.
The slope of the graph is zero indicating that the velocity of the particle, both instantaneous and average, is zero.
The intercept xo of the graph on the position axis gives the position of the stationary particle with respect to the reference point, origin O (i.e., its distance from O).
(ii) Position-time graphs (x-t graph) for a particle moving with uniform velocity in the +x and –x direction :
The graph is a straight line inclined to the time axis. The straight line nature (or constant slope) of the graph indicates that there is equal displacement in equal intervals of time, i.e., the motion is uniform.
The slope of the straight line gives the magnitude of the average velocity, which is also equal to the instantaneous velocity of the particle.
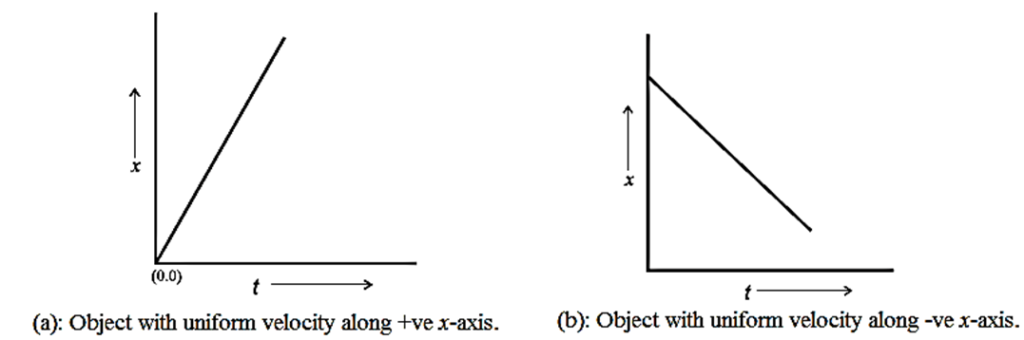
If the slope is positive, Fig. (a), the instantaneous velocity is positive which indicates that the particle is moving in the direction of increasing x.
If the slope is negative, Fig. (b), the instantaneous velocity is negative which indicates that the particle is moving in the direction of decreasing x.
(iii) Position-time graphs (x-t graph) for a particle performing oscillatory motion :
The particle moves back and forth about an equilibrium or mean position x0 over the same path. The direction of velocity reverses over equal intervals of time. Thus, it is a nonuniform (accelerated) periodic motion.
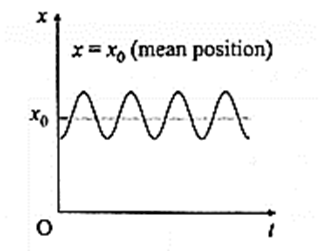
Fig.- Position-time graphs for a particle performing oscillatory motion
Position-time graph of a nonuniform (i.e., accelerated) one-dimensional motion : Hence explain its average velocity and instantaneous velocity. (2 marks)
If a particle undergoes a nonuniform (i.e. accelerated) motion during a certain time interval, then its x-t graph is non-linear in that time interval, i.e., it is a curve whose slope is different at different points.
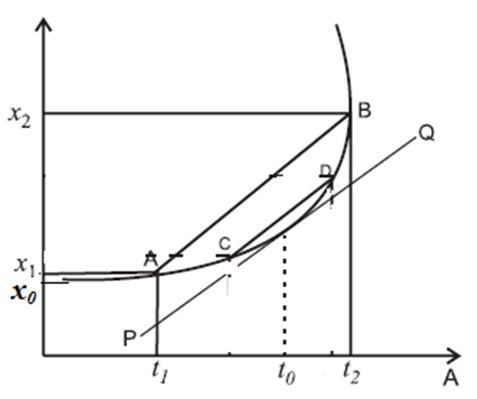
Fig-Position-time graph of a nonuniform (i.e., accelerated) motion
Figure shows the x-t graph of a particle starting at x = x0 and moving in the direction of the + x-axis with increasing velocity. The average velocity of the particle in the time interval Δt = t2 — t1 is the slope of the chord AB :
\(v_{av}=\frac{Δx}{Δt}=\frac{x_2-x_1}{t_2-t_1}\)
The instantaneous velocity of the particle at any instant t0 is given by the slope of the tangent to the curve at t0 :
\(v_{av}=\lim_{Δt-0}\frac{Δx}{Δt}=\frac{dx}{dt}\)
Position-time graph examples :
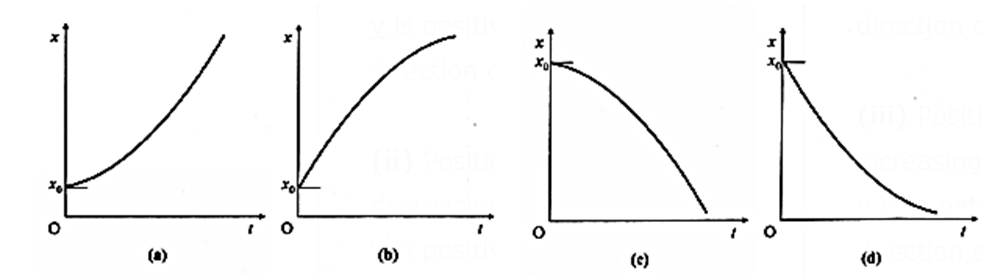
Fig (a) : Position-time graphs for a particle whose instantaneous velocity (v) is positive and increasing : The particle is moving in the direction of increasing x.
Fig (b) : Position-time graphs for a particle whose instantaneous velocity (v) is positive and decreasing : The particle is moving in the direction of increasing x.
Fig (c) : Position-time graphs for a particle whose instantaneous velocity (v) is negative and increasing : The particle is moving in the direction of decreasing x.
Fig (d) : Position-time graphs for a particle whose instantaneous velocity (v) is negative and decreasing : The particle is moving in the direction of decreasing x.
Acceleration:
Accelerated motion : A particle is said to be in an accelerated motion if its velocity changes with time in magnitude or direction or both.
- The acceleration is uniform or constant if there is equal change in velocity in equal intervals of time, however small the time interval may be.
- Acceleration is a vector quantity and its dimensions are [L1M0 T-2].
Average acceleration : The average acceleration of a particle is defined as the change in its instantaneous velocity \(Δ\vec{v}\) divided by the elapsed time interval Δt.
\(\vec{a}_{av}=\frac{Δ\vec{v}}{Δt}\)
where \(Δ\vec{v}=\vec{v_f}-\vec{v_i}\) and \(Δ\vec{t}=\vec{t_f}-\vec{t_i}\) . The direction of \(\vec{a}_{av}\) is the same as that of \(Δ\vec{v}\).
Instantaneous acceleration : The acceleration at a given instant is called the instantaneous acceleration, and is defined as the limiting value of the average acceleration as the time interval approaches zero.
\(\vec{a}=\lim_{Δt→0}\frac{Δ\vec{v}}{Δt}\)
- In general, when we say acceleration, we mean instantaneous acceleration
- Instantaneous acceleration is the slope of the tangent to the velocity-time graph at a given instant.
Uniform acceleration : When the acceleration is constant, both in magnitude and direction, it is called uniform acceleration.
In such a case,
- the instantaneous acceleration equals the average acceleration
- the velocity changes linearly with time
- the average velocity is the algebraic mean of the initial and final velocities, i.e., if \(\vec{u}\) and \(\vec{v}\) are the initial and final velocities respectively,
average velocity = \(\frac{1}{2}(\vec{u}+\vec{u})\)
Q. State the condition(s) under which the magnitude of displacement of a particle equals the path length travelled.
Ans. The magnitude of the displacement of a particle equals the path length travelled if
- The direction of motion does not change in the given time interval, i.e., if the acceleration is zero or along the direction of the velocity
- The particle is at rest.
Retardation or deceleration : The motion of a particle is said to be accelerated if the velocity of the particle changes with time. When the instantaneous speed of a body decreases with time, the acceleration is opposite to the instantaneous velocity and is called retardation or deceleration.
- It is not always correct to say that deceleration is negative acceleration. For example, for a particle moving in the negative x direction, an acceleration in the positive x direction is a deceleration
Velocity-time graph : The velocity-time graph for a particle is a plot of the velocity v of the particle against time t.
- Time is the independent variable and plotted on the x-axis.
- The velocity of the particle is the dependent variable and is plotted on the y—axis (according to the Cartesian sign convention).
Velocity-time graph for a particle moving with constant velocity along the positive x-axis :
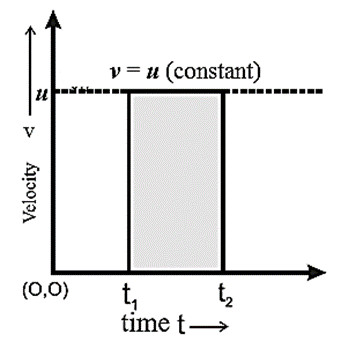
- The graph v = u is a straight line parallel to the time axis which means that the velocity of the particle is independent of time.
- The slope of the graph is zero indicating that the acceleration of the particle, both instantaneous and average, is zero.
- The intercept u of the graph on the velocity axis gives the initial velocity of the particle.
- The area under the line between t1 and t2 gives the magnitude of the displacement Ax during the time interval Δt = t2 — t1.
Velocity-time graphs for a particle moving with constant acceleration :
Consider a particle moving along the positive x—axis.
- The graph is a straight line inclined to the time axis.
- The straight line nature, i.e., the constant slope, of the graph indicates that there is equal change in velocity in equal intervals of time, however small the time interval may be. That is, the acceleration is constant.
- The slope of the straight line gives the average acceleration which is also equal to the instantaneous acceleration of the particle.
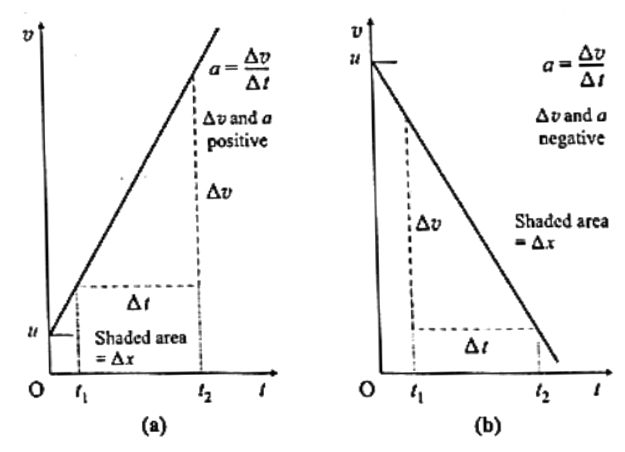
The v-t graph for a particle moving with constant
(a) positive acceleration (b) negative acceleration
- If the slope is positive, the instantaneous acceleration is positive. If the slope is negative, the instantaneous acceleration is negative.
- The intercept u of the graph on the velocity axis gives the initial velocity of the particle. If the particle starts from rest (u = 0), the graph passes through the origin.
- The area under the line between t1 and t2 gives the displacement Δx during the time interval Δt = t2 — t1.
Velocity-time graph of a particle moving with a nonuniform acceleration :
If the velocity of a particle changes during a certain time interval, then its v-t graph is non-linear in that time interval, i.e., it is a curve whose slope is different at different points.
- Figure (a) shows the v-t graph of a particle which starts from rest and moves in the +x direction with increasing velocity and increasing acceleration. The slope is positive and increases with time.
- Figure (b) shows the v-t graph of the particle if it has decreasing acceleration.
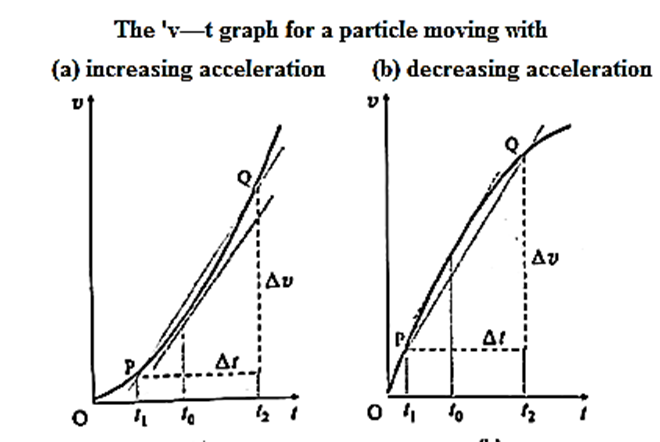
The average acceleration of the particle in the time interval Δt = t2 — t1 is the slope of the Chord PQ :
\(a_{av}=\frac{dv}{dt}=\frac{v_2-v-1}{t_2-t_1}\)
The instantaneous acceleration of the particle at any instant t0 is given by the slope of the tangent to the curve at t0 :
a = \(\lim_{Δt→0}\frac{Δv}{Δt}\)
The shaded area under the curve between t1 and t2 is the displacement of the particle during that time interval given by
\(\int_{t_1}^{t_2}vdt=\int_{t_1}^{t_2}\frac{dx}{dt}dt=\int_{t_1}^{t_2}dx=x(t_2)-x(t_1)\)
Q. (i) What kind of a velocity-time graph has average and instantaneous velocities always equal? (ii) What is the nature of the corresponding position-time graph?
Ans. (i) If the instantaneous velocity of a particle is always equal to its average velocity, the particle must be moving with a constant velocity. Hence, the velocity-time graph is a straight line parallel to the time axis.
(ii) The corresponding position-time graph of the particle is a straight line. The slope of the line is positive if the particle is moving in the direction of increasing x, or negative if it is moving in the direction of decreasing x.
Q. Can the velocity of a particle be equal to - zero at a given instant, and yet be varying with time? Explain with two examples.
Ans. A deceleration can reduce the velocity of a particle to zero and then increase it in a direction opposite to its initial velocity. At the turning point of the motion, the particle has an acceleration but its instantaneous velocity is zero
Examples : (1) When a particle is thrown straight up, the Earth's gravitational force, being downward, decelerates the particle until its velocity becomes momentarily zero. At this peak point of its motion, the particle has zero instantaneous velocity but constant downward acceleration.
(2) When a particle performs oscillatory motion, at both the extreme positions (the turning points) of the motion, the particle has zero instantaneous velocity and a non-zero acceleration.
| Always Remember:
For uniform acceleration, for a rectilinear motion:
For nonuniform acceleration in a rectilinear motion:
While using the concept of area under the curve, the origin of the velocity axis (for v-t graph) must be zero. |
Equations of Motion for Uniform Acceleration:
We can graphically derive Newton's equations of motion for an object moving with uniform acceleration.
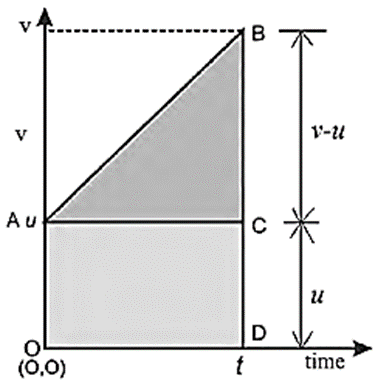
Consider a particle moving in a straight line with an initial velocity u and constant acceleration a. The v—t graph is a straight line with slope a and y-intercept u. With u and a both positive, the graph is as shown in Fig.
The slope of the line gives the acceleration of the particle,
a =\(\frac{Δv}{Δt}=\frac{v-u}{t-0}=\frac{v-u}{t}\)
∴ v = u + at
This is the first equation of motion (or the first kinematical equation).
The area under the ‘straight line for a time interval Δt = t − 0, as shown by the shaded region,
area of rect. OACD + area of Δ ABC
= (OA x AC) + \(\frac 12\)(AC x BC)
= ut + \(\frac 12\)t(v − u)
= ut + \(\frac 12\)at2 ( '.' v−u = at)
= s, distance covered in the elapsed time t.
∴ s = ut + \(\frac{1}{2}\)at2
This is the second equation of motion (or the second kinematical equation).
[Alternatively, the shaded area = area of the trapezium OABD = (\frac 12\)(OA + BD) x OD
= \(\frac 12\)(v + u)t
= vav t .... { '.' vav = \(\frac 12\)(v + u)}
= distance covered in the elapsed time t]
∴ s =\ (\frac 12\)(u + v)\((\frac{v-u}{a})\)
substituting for t from the first kinematical equation. '
∴ s = \((\frac{v^2-u^2}{2a})\)
∴ v2 = u2 + 2as
This is the third equation of motion (or the third kinematical equation).
Free fall : When a body starts with zero velocity at a certain height from the ground and falls under the influence of the gravity of the Earth, ignoring air resistance and buoyancy of air, it is said to be in free fall.
Kinematical equations as applied to one-dimensional vertical motion of a body near the Earth's surface :
Free fall near the Earth's surface is one of constant downward gravitational acceleration ( ).
We assign a positive value to a vector directed vertically up and a negative value if it is directed vertically down.
Hence, for one-dimensional vertical motion of a body, its acceleration \(\vec{g}\)
a ≡ ay = — g. Then, the kinematical equations are, in usual notation,
v = u – gt ….. (1)
s = ut − \(\frac 12\)gt2 ….. (2)
v2 = u2 – 2gs ….. (3)
For a body released from rest and falling freely under gravity : (Ignore air resistance and the buoyancy of air).
we substitute u = 0 in the above equations.
v = – gt ……(4)
s = − \(\frac 12\)gt2 ….. (5)
v2 = – 2gs ….. (3)
Here, g =| \(\vec{g}\) | ≅ 9.8 m/s2.
Relative velocity in the case of one-dimensional motion :
Motion is relative, i.e., motion of a body can be defined only with respect to an observer.
The velocity determined by a particular observer is called the velocity relative to that observer, or simply, relative velocity.
(i) If two bodies A and B are moving in the same direction, the velocity of A relative to B is vAB = vA − vB.
If vA > vB, then vAB has the same direction as vA and vB, so that as observed from B, A appears to be moving ahead with velocity
vAB (see Fig.).
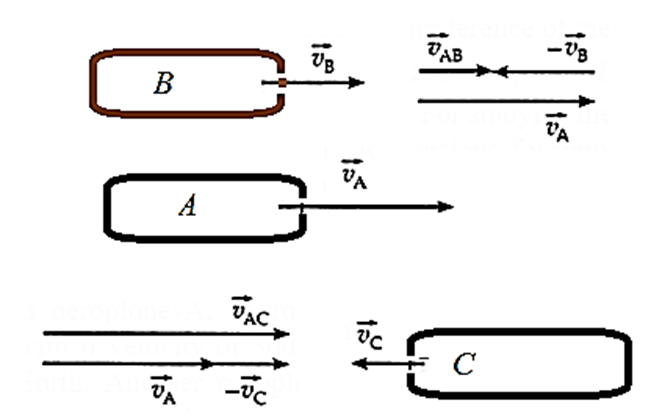
Since vBA = − vAB when observed from A, B appears to be receding (i.e., moving backwards) with velocity vBA.
If A was initially behind B, then as observed from B, A appears to be approaching with velocity vAB} as observed from A, B appears to be approaching with velocity vBA.
(ii) If two bodies A and C are moving in opposite directions, we may take the velocity of one, say vA, as positive and that of the other as negative. Then, the relative velocity of A with respect to C is
vAC = vA − (−vC) = vA + vC
So, when observed from C, A appears to be approaching C with velocity vAC (See Fig)
Since vCA = −vAC; when observed from A, C appears to be approaching A with velocity vCA
After A and C cross each other, when observed from C, A appears to be receding with velocity vAC; when observed from A, C appears to be receding with velocity vCA.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 2: Mathematical Methods – Online Notes
Next Chapter : Chapter 4: Laws of Motion – Online Notes
do you have an app for your notes?
currently not, planning for it