Thermal Properties of Matter
Maharashtra Board-Class-11-Science-Physics-Chapter-7
Notes Part-2
Topics to be Learn : Part-2
|
Specific Heat Capacity :
Specific Heat Capacity of Solids and Liquids :
Definition : The specific heat capacity of a substance is defined as the amount of heat per unit mass absorbed or given out by the substance to change its temperature by one unit (one degree). i.e., 1 °C or 1 K.
Example :
- The specific heat capacity of gold is 134 J/kg- °C. This means 134 J of heat per kg of gold must be transferred to the metal to increase its temperature by 1 °C.
SI unit : The joule per kilogram-kelvin (J/kg.K). (1 J/kg.°C = 1J/kg.K)
CGS unit : The erg per gram-degree Celsius (erg/g.°C) (1 erg/g.°C = 1 erg/g.K)
If ΔQ is the amount of heat absorbed or given out by a body of mass m so that its temperature changes from T1 to T2, the specific heat capacity of its material is given by
S = \(\frac{ΔQ}{mΔT}\)
Molar specific heat capacity : The molar specific heat capacity of a substance
is the amount of heat per mole absorbed or given out by the substance to change its
temperature by 1 °C or 1 K.
C = \(\frac{1}{n}\frac{ΔQ}{ΔT}\)
where C = molar specific heat capacity
n = amount of substance in moles
ΔQ = amount of heat energy absorbed or given out
ΔT = change in temperature
The SI unit of molar specific heat capacity is J/mol.K. (1J/mol.°C = 1J/mol.K).
Specific Heat Capacity of Gas:
In case of a gas, slight change in temperature is accompanied with considerable changes in both, the volume and the pressure.
If gas is heated at constant pressure, volume changes and therefore some work is done on the surroundings during expansion requiring additional heat. As a result, specific heat at constant pressure (Sp) is greater than specific heat at constant volume (Sv). It is thus necessary to define two principal specific heat capacities
for a gas.
Explanation :
If Q is the amount of heat supplied to a substance of mass m and ΔT is the rise in
temperature of the substance, the specific heat of the substance is
s = \(\frac{ΔQ}{mΔT}\)
When a gas is heated isothermally,
Q ≠ 0 but ΔT = 0
∴ s = ∞
On the other hand, if a gas is compressed or allowed to expand adiabatically, i.e., no heat enters or leaves the gas, its temperature changes
but Q = 0 ∴ s = 0
Thus, it can be seen that the specific heat capacity of a gas can have any value from 0 to ∞, depending upon the conditions under which it is heated. Therefore, to fix the value of the specific heat capacity of a gas, in practice, either the volume or the pressure is kept constant.
These two being the most important or principal conditions under which a gas is usually heated,
we define two principal specific heat capacities for a gas, namely, (i) specific heat capacity at constant volume (Sv) and (ii) specific heat capacity at constant pressure (Sp)
Principal specific heat capacity of a gas at constant volume : The principal specific heat capacity of a gas at constant volume (Sv) is defined as the quantity of heat absorbed or released to increase or decrease the temperature of unit mass of the gas through one kelvin (or 1 °C), when its volume is kept constant.
Principal specific heat capacity of a gas at constant pressure : The principal specific heat capacity of a gas at constant pressure (Sp) is defined as the quantity of heat absorbed or released to increase or decrease the temperature of unit mass of the gas through one kelvin (or 1 °C), when its pressure is kept constant.
Molar specific heat capacity of a gas at constant volume : The molar specific heat capacity of a gas at constant volume (CV) is defined as the quantity of heat absorbed or released to increase or decrease the temperature of one mole of the
gas through one kelvin (or 1°C), when its volume is kept constant.
Molar specific heat capacity of a gas at constant pressure : The molar specific heat capacity of a gas at constant pressure (Cp) is defined as the quantity of heat absorbed or released to increase or decrease the temperature of one mole of the gas through one kelvin (or 1 °C), when its pressure is kept constant.
[Note : The adjective ‘specific’ means ‘per unit mass . Hence, it is proper to say ’molar heat capacity’, and not molar specific heat capacity]
Relation between principal and molar specific heat capacities :
Molar specific heat capacity = molar mass x principal specific heat capacity.
i.e. CP = M x SP and CV = M x SV
where M = molar mass of the gas
Cp =molar specific heat capacity at constant pressure
Sp = principal specific heat capacity at constant pressure
CV = molar specific heat capacity at constant volume
Sv = principal specific heat capacity at constant volume
Formula for heat absorbed or given out by a substance in terms of its specific heat capacity :
Suppose a substance of mass m and specific heat capacity s is heated or cooled so that its temperature increases or decreases by ΔT. Then the heat absorbed or given out by the substance is Q = ms ΔT
Heat capacity (or thermal capacity) of a body :
- The heat capacity (or thermal capacity) of a body is the amount of heat to be given to the body or to be removed from the body to increase or decrease its temperature by 1 °C or 1 K.
- Heat capacity of a body = mass of the body x the specific heat capacity of its material
- Different materials have different specific heat capacities. Hence, bodies of equal mass but different materials have different heat capacities.
- Bodies of the same material but different masses have different heat capacities.
- The amount of heat Q required to raise the temperature of a substance depends on (i) the nature of the material (ii) the mass of the material m (iii) the temperature rise Δ Q ∝ m and Q ∝ ΔT
Relation between the heat capacity and the specific heat capacity of a body:
Specific heat capacity = heat Capacity/mass OR
Heat capacity = mass x specific heat capacity [Q= ms]
Q. Explain why the specific heat capacity of a gas at constant pressure is greater than that at constant volume.
- When a gas is heated at constant volume, the work done by the gas against the external pressure is zero. Hence, all the heat supplied to it is used to raise its temperature.
- On the other hand, when the gas is heated at constant pressure, there is a considerable increase in its volume. A part of the heat supplied to it is used to do work against the external pressure in pushing back the surrounding air. Therefore, only the remaining part of the heat supplied to it is used to raise its temperature.
- Hence, for the same rise in temperature in the two cases, the heat to be supplied for heating at constant pressure is greater than that for heating at constant volume. Therefore, the specific heat capacity of a gas at constant pressure is greater than that at constant volume.
Calorimetry:
Calorimetry is an experimental technique for the quantitative measurement of heat
exchange. To make such measurement a calorimeter is used.
Calorimeter :
- A calorimeter is a cylindrical copper vessel kept on an insulating support and enclosed in an insulating jacket such as a wooden box with a lid.
- The lid has two narrow holes, one for the stirrer and the other for a thermometer.
- The outer and the inner surfaces of a calorimeter are polished to reduce the exchange of heat between the calorimeter and its surroundings by radiation.

- The space between the copper vessel and the outer insulating jacket is filled with a bad conductor of heat such as felt or glasswool to reduce the exchange of heat with the surroundings by conduction.
- The lid made of insulating material such as wood reduces the exchange of heat with the surroundings by convection.
- A calorimeter is used to determine the specific heat of a substance using the law of conservation of energy.
Principle of heat exchange : The principle of calorimetry is derived from the law of conservation of energy.
- When a hot body and a cold body are kept in good thermal contact, there is a net transfer of heat from the hot body to the cold body till both of them attain the same temperature.
- When there is no exchange of heat between the system of two bodies and the surroundings, heat lost by the hot body = heat gained by the cold body
- This result is also known as the principle of heat exchange.
The method of mixtures to determine the specific heat of an insoluble solid :
The specific heat of the material of an insoluble solid can be determined by the ‘method of mixture’ using the principle of heat exchange : If a system of two bodies at different temperatures is isolated from the surroundings, the heat lost by the hot body = the heat gained by the cold body.
- In this method, a calorimeter is partially filled with known quantity of water at a particular temperature.
- A sample of the material of known mass is heated to the steam point and then quickly transferred to the calorimeter.
- The contents are stirred constantly until the mixture attains a final common temperature.
- The heat lost by the sample is gained by the water and the calorimeter.
Let m1 = mass of the sample
m2 = mass of the calorimeter and the stirrer,
m3 = mass of the water in the calorimeter,
s1 = specific heat capacity of the material of sample
s2 = specific heat capacity of the material of the calorimeter and stirrer,
s3 = specific heat capacity of water,
T1 = initial temperature of the sample
T2 = initial temperature of the calorimeter, stirrer and water,
T = final temperature of the combined system (mixture),
The heat lost by the sample = m1s1 (T1 — T)
The heat gained by the calorimeter and the stirrer = m2S2(T — T2)
The heat gained by the water = m3s3 (T — T2)
Assuming that there is no exchange of heat between the system and the surroundings, the heat lost by the sample is gained by the calorimeter, stirrer and water.
Thus,
m1s1 (T1 — T) = m2s2(T — T2) + m3s3 (T — T2) ……(1)
The specific heat capacity of the material of sample,
s1 = \(\frac{(m_2s_2+m_3s_3)(T-T_2)}{m_1(T_1-T)}\) ….(2)
The specific heat capacity of water or any liquid can be determined using the equation.
s3 = \(\frac{m_1s_1(T_1-T)}{m_3(T-T_2)}-\frac{m_2s_2}{m_3}\) …..(3)
when all other quantities are known.
[Note : In this experiment, the heat from the solid sample is given to the liquid and therefore the sample should be denser than the liquid, so that it does not float on the liquid.]
Equilibrium temperature : When two bodies in good thermal contact are in thermal equilibrium, their common temperature is called the equilibrium temperature.
Change of State:
Phase change or change of state :
There are three states of matter : liquid, solid and gas. A transition from one of these states to another is called a change of state.
- It is invariably accompanied by the evolution or absorption of heat usually at constant temperature.
- Two common changes of states are solid to liquid and liquid to gas (and vice versa). These changes can occur when exchange of heat takes place between the substance and its surroundings.
Activity : To understand the process of change of state:
- Take some cubes of ice in a beaker.
- Note the temperature of ice (0 °C). Start heating it slowly on a constant heat source.
- Note the temperature after every minute.
- Continuously stir the mixture of water and ice. Observe the change in temperature.
- Continue heating even after the whole of ice gets converted into water.
- Observe the change in temperature as before till vapours start coming out.
- Plot the graph (along x-axis). You will obtain a graph of temperature versus time as shown in Fig.
Analysis of observations :
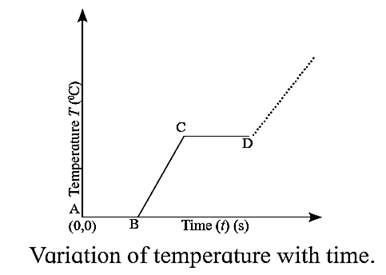
- Initially, the temperature of the melting ice is 0 °C. There is no change in the temperature until all the ice melts even though heat is supplied continuously. This is shown in the θ — t graph by the line AB parallel to the t-axis.
- It implies that during the solid—>liquid phase change, heat is absorbed at constant temperature and both states coexist in thermal equilibrium.
- The constant temperature for this solid—>liquid phase change is the melting point.
- After all the ice has melted, the temperature of liquid water rises on further heating up to the point C, when it again becomes steady.
- The heat absorbed is now utilized for the liquid—>vapour phase change.
- The temperature remains constant till all the liquid water is vaporized, as shown by the line CD parallel to the t-axis.
- The constant temperature for this liquid—>vapour phase change is the boiling point.
- After Point D : For a liquid in an open beaker in contact with air at 1 atm pressure, the temperature does not change. But, in a closed system, steam can be heated to temperatures much above 100 °C.
Melting point : The temperature at which a solid melts, i.e., a substance changes from solid to liquid, at constant pressure is called its melting point at that pressure.
Effect of pressure on melting point : For a material which expands on melting, an increase in pressure increases its melting point. For a material which contracts on melting, an increase in pressure lowers its melting point.
Fusion or freezing : The phase transition from liquid to solid is called fusion or freezing. At a given pressure, the transition between liquid and solid states occur at the same temperature, i.e., the fusion or freezing point is the same as the melting point.
Boiling point : The temperature at which a liquid boils off, i.e., a substance changes from liquid to gaseous state, at constant pressure is called its boiling
or vaporization point at that pressure.
Effect of pressure on boiling point : The boiling point of a liquid rises with an increase in pressure on the liquid surface.
Condensation or liquefaction : The phase transition from vapour to liquid is called condensation or liquefaction. At a given pressure, the transition between gaseous and liquid states occur at the same temperature, i.e., the condensation point is the same as the boiling point.
Normal boiling point : The temperature at which a liquid boils off at standard pressure is called its normal boiling point.
Sublimation:
- Sublimation is the direct phase transition from solid to gaseous state without passing
- through the intermediate liquid state.
- The reverse phase transition from gaseous state to solid state is called deposition
Phase diagram :
- A phase diagram is a graphical representation of the physical states of a substance in a closed system under different conditions of temperature and pressure.
- A phase diagram has pressure (typically in atmosphere) on the y-axis and
- temperature (typically in kelvin or degree Celsius) on the x-axis.
Features of a phase diagram :
A typical phase diagram consists of discrete regions that represent the different phases of a substance in a closed system. Each region corresponds to the range of combinations of temperature and pressure over which that phase is stable.
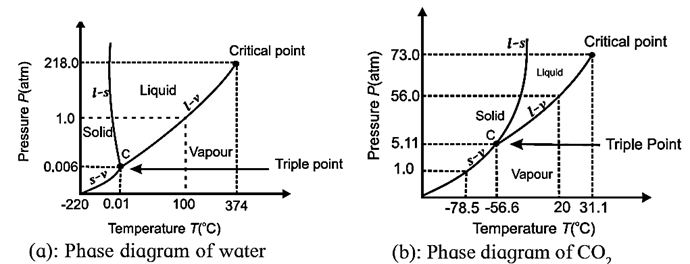
The curves in a phase diagram correspond to the combinations of temperature and pressure at which two phases can coexist in equilibrium.
The three main curves are :
- (i) Fusion or freezing curve : A fusion curve on a phase diagram divides the solid and liquid phases of a substance and represents fusion or melting (solid to liquid) and freezing (liquid to solid). Thus, it is a graph of freezing or melting point against pressure. At points on the curve the two phases coexist in equilibrium.
- (ii) Vaporization or condensation curve : A vaporization curve on a phase diagram divides the liquid and gas phases of a substance and represents vaporization (liquid to gas) and condensation (gas to liquid). Thus, it is a graph of boiling or condensation point against pressure. It ends at the critical point. At points on the curve, the liquid and vapour phases coexist in equilibrium.
- (iii) Sublimation or deposition curve : A sublimation curve on a phase diagram divides the solid and gaseous phases of a substance and represents sublimation (solid to vapour) and deposition (vapour to solid). Thus, it is a graph of sublimation or condensation point against pressure. It is also known as the vapour pressure curve of the solid phase. At points on the curve, the solid is in equilibrium with the vapour phase through sublimation and deposition.
A phase change occurs as we cross a curve on the phase diagram. There are also two important points on the diagram :
- (i) Triple point is the point at which the fusion curve, vaporization curve and sublimation curve meet. It is the only combination of temperature and pressure at which all the three phases of matter are in equilibrium and can therefore exist simultaneously.
- (ii) Critical point is the point at which the substance is indistinguishable between liquid and gaseous states. It terminates the vaporization curve.
The solid phase is favoured at low temperature and high pressure; the vapour phase is favoured at high temperature and low pressure. The combination of high temperature and high pressure corresponds to saturated gas.
With most substances, the temperature and pressure related to the triple point lie below the standard temperature and pressure, and the pressure for the critical point lies above the standard pressure. Therefore, at standard pressure as temperature increases, most substances change from solid to liquid to gas; and at standard temperature as pressure increases, most substances change from gas to liquid to solid.
Know This :
|
Gas and Vapour:
Critical temperature : A gas must be cooled to a certain temperature in order to liquefy it by application of pressure. This temperature is called critical temperature.
Gas : A substance which is in the gaseous phase and at a temperature above its critical temperature is called a gas.
Vapour : A substance which is in the gaseous phase and at a temperature below its critical temperature is called a vapour.
Latent Heat:
Latent heat is the amount of heat that must be given to a substance at a constant temperature to change its state.
- SI unit : The joule (I).
- CGS units : The erg (mechanical unit) and the calorie (heat unit).
Specific latent heat : Specific latent heat of a substance is the amount of heat that must be given to a unit mass of the substance at a constant temperature to change
its state.
- SI unit : The joule per kilogram (J/kg).
- CGS units : The erg per gram and the calorie per gram (cal/g).
The quantity of heat absorbed or released by a mass m of a substance while undergoing a change of state is
Q = mL
where L = specific latent heat of the substance, a characteristic of the substance.
Latent heat of fusion : Latent heat of fusion is the amount of heat that given to a substance at a constant temperature to change its state from solid to must be
liquid. Latent heat of fusion per unit mass of a substance is called its specific latent heat of fusion,
Latent heat of vaporization : Latent heat of vaporization is the amount of heat that must be given to a substance at a constant temperature to change its state from liquid to vapour. Latent heat of vaporization per unit mass of a substance is called its specific latent heat of vaporization.
Latent heat of fusion and vaporization for water :
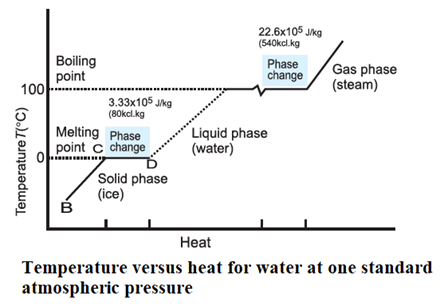
For water the latent heat of fusion and vaporisation are Lf = 3.33 × 105J kg-1 and Lv = 22.6×105J kg-1 respectively. That is 3.33 x 105 J of heat is needed to melt 1kg of
ice at 0 °C and 22.6 × 105 J of heat is needed to convert 1 kg of water to steam at 100 °C. Hence, steam at 100°C carries 22.6 × 105 J kg-1 more heat than water at 100 °C. This is why burns from steam are usually more serious than those from
boiling water.
Know This :
|
Heat Transfer:
- Heat transfer from one point of body to another in three different ways- by conduction, convection and radiation.
- Heat transferes through solids by conduction. In this process, heat is passed on from one molecule to other molecule but the molecules do not leave their mean positions.
- Liquids and gases are heated by convection. In this process, there is a bodily movement of the heated molecules.
- In order to transfer heat by conduction and convection a material medium is required.
- Transfer of heat by radiation does not need any medium. Radiation of heat energy takes place by electromagnetic (EM) waves.
- Conduction is a slow process of heat transfer while convection is a rapid process. Radiation is the fastest process because the transfer of heat takes place at the speed of light.
Conduction:
Thermal conduction : Thermal conduction is the mechanism of heat transport within a body or between two bodies in contact from a region of high temperature to a region of lower temperature without the migration of the particles of the medium.
- The atoms in a solid constantly vibrate about their mean positions. The amplitude of vibration increases with temperature. The energy of these vibrations is transmitted to cooler regions mainly by collisions with neighbouring atoms possessing lower kinetic energy. This is how most materials conduct heat.
- Pure metals, however, conduct heat mainly by means of fast-moving free electrons in a manner analogous to the conduction of electricity. This accounts for the fact that pure metals have values of thermal conductivity one or two orders of magnitude higher than insulating solids
Conduction in metal : A material which readily conducts heat is called a good conductor of heat. A material which does not conduct heat readily is called a poor or bad conductor of heat or a thermal insulator.
- Conduction of heat by metals is predominantly by the transport of fast-moving free electrons, in a manner analogous to their conduction of electricity.
- In solid insulators, which do not have free electrons, thermal conduction is only by the vibrations of its atoms.
- Hence, because of the more efficient mechanism of heat transfer by free electrons, pure metals are good conductors of heat (and electricity), e.g., silver, copper, alurninium,brass, etc., while non metals are bad conductors of heat (and electricity), e.g., wood, cloth, air, paper, etc..
Thermal Conductivity:
Steady state : A thick metal rod of uniform cross section has one of its ends, A, maintained at a constant temperature by steam, see below Fig.
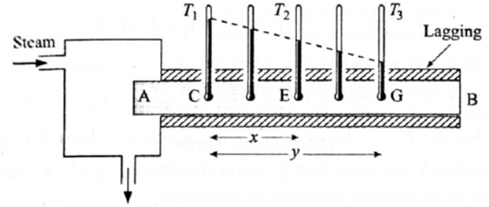
The opposite end B is maintained at a constant lower temperature. The rod is covered with a thermal insulator (such as felt, slag wool or glass fibres — such materials are then called lagging) to prevent any heat loss from its longer surface. Thermometers are placed in holes drilled into the rod, with a small amount of mercury in each hole to ensure good thermal contact between the rod and the bulb of a thermometer.
Initially, as the end A is heated by steam, all the thermometers show a gradual rise in temperature. The section nearest to the steam end A always remains hottest. At this stage, as heat is being conducted, every section of the rod retains a part of this heat (which raises its temperature) and transmits the rest to the next section. After some time, the thermometer readings become stable, indicating that there is no further rise in the temperature of any section of the rod. Then, the rod is said to be in a thermal steady state.
Temperature gradient : When a solid conducting heat is in a thermal steady state, if T1 and T2 are the temperatures of two sections, which are transverse to the direction of heat conduction and a distance x apart, the quantity is called the temperature gradient.
In above Fig., if T1, T2, T3 are the readings in the thermometers at C, E and G respectively, it is found that, \(\frac{T_1-T_2}{x}=\frac{T_1-T_3}{y}\) i.e., the temperature gradient along a lagged rod in the steady state is constant.
Coefficient of thermal conduction :
The rate at which heat is conducted through two parallel surfaces of a block in the steady state divided by the area of cross section and the temperature gradient is called the thermal conductivity or coefficient of thermal conduction of the material.
Expression Coefficient of thermal conduction:
Let PQ be a small section of length x of a lagged rod in a thermal steady state. The stable temperature at the end P is T1 and that at the end Q is T2 < T1. The lagging ensures that there is no loss of heat to the surroundings through the cylindrical surface of the rod. Hence, all the heat passes through the rod in a direction normal to the cross sections P and Q, Fig.
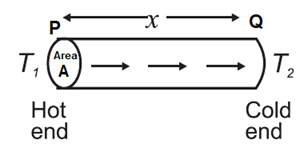
Since the rod is in a steady state, the quantity of heat entering per unit time through the end P of the section must be equal to that leaving the end Q.
It is found experimentally that the quantity of heat Q that flows from hot end to the
cold end is directly proportional to,
- the time t
- the cross-sectional area A
- the temperature difference between the two ends (T1 − T2).
and is inversely proportional to
- The perpendicular distance x between hot and cold ends
That is,
Q ∝ A\((\frac{T_1-T_2}{x})\)t
∴ Q = kA\((\frac{T_1-T_2}{x})\)t
where k is a constant of proportionality and is called the thermal conductivity. Thus, the thermal conductivity can be written as,
k = \(\frac{Qx}{A(T_1-T_2)t}\)
SI unit of coefficient of thermal conductivity k is Js−1m−1°C−1 or Js−1m−1K−1 or watt per meter kelvin (W/m.K)
CGS units : the erg per second centimeter degree Celsius (erg/s.cm.°C) and the calorie per second centimetre degree Celsius (cal/s.cm. °C).
Dimensions : [MLT−3K−1]
Significance of thermal conductivity :
- For a given surface area, thickness and temperature difference, thermal conductivity indicates how quickly a material would conduct heat through it.
- A material with a large thermal conductivity is a better conductor of heat.
- Generally, good thermal conductors are also good electrical conductors.
Thermal Resistance (RT):
The opposition to the flow of heat through a body is called thermal resistance.
Definition : Thermal resistance is defined as the ratio of the temperature difference between the two parallel faces of a material to the rate at which heat is conducted through those surfaces.
If Q is the quantity of heat conducted between two parallel surfaces of a slab in time t, the heat conduction rate is
Q/t = kA\((\frac{T_1-T_2}{x})\)
Where k = the thermal conductivity of the A material,
A = the cross-sectional area of each surface,
X = the perpendicular distance between the two surfaces,
T1 — T2 = the temperature difference between the two surfaces.
Then, the thermal resistance of the slab is,
RT = \((\frac{T_1-T_2}{Q/t})\) = \((\frac{x}{kA})\)
Dimensions = [RT] = [M−1L−2T3K1].
SI unit : The kelvin second per joule K.s/J
Applications of Thermal Conductivity:
(i) Cooking utensils are constructed of metal yet have handles made of poor conductors. Because metals conduct heat well, heat can quickly pass through the base of the kitchenware. Utensil handles are made of poor heat conductors (e.g., wood, ebonite, etc.) and hence cannot transport heat from the utensils to our hands.
(ii) Thick walls are used in the construction of cold storage rooms. Brick is a bad
conductor of heat so that it reduces the flow of heat from the surroundings to the rooms. Still better heat insulation is obtained by using hollow bricks. Air
being a poorer conductor than a brick, it further avoids the conduction of heat from outside.
(iii) To prevent ice from melting it is wrapped in a gunny bag. A gunny bag is a poor
conductor of heat and reduces the heat flow from outside to ice. Moreover, the
air filled in the interspaces of a gunny bag, being very bad conductor of heat, further avoids the conduction of heat from outside.
(iv) Copper is the third best heat conductor after gold and silver. As a result, the tubings inside an air conditioner and a solar water heater are composed of copper, which swiftly transfers heat from the surrounding environment or the sun's rays to the fluid inside. Similarly, the electrical heating element of a water heater is housed within an insulated copper tubing that rapidly transports heat from the heating element to the water outside.
Convection:
Definition : The process by which heat is transmitted through a substance from one point to another due to the actual transport of the heated particles of the substance is called convection.
- In convection, heat is transmitted from one point to another by the actual bodily movement of the heated (energised) molecules within the fluid.
- In liquids and gases heat is transmitted by convection because their molecules are quite free to move about.
Consider a liquid in a beaker being heated from below. The liquid at the bottom absorbs heat before the rest of the liquid and its density diminishes. This warmer and lighter liquid rises up and is replaced by cooler denser part of the liquid. This, in turn, is heated and rises. This circulatory movement of the fluid is called convection current, and the transmission of heat by migration of the particles of the medium is called convection.
Applications of Convection:
- i) Heating and cooling of rooms : The mechanism of heating a room by a heat convector or heater is entirely based on convection. The air molecules in immediate contact with the heater are heated up. These air molecules acquire sufficient energy and rise upward. The cool air at the top being denser moves down to take their place. This cool air in turn gets heated and moves upward. In this way, convection currents are set up in the room which transfer heat to different parts of the room. The same principle but in opposite direction is used to cool a room by an airconditioner.
- ii) Cooling of transformers : Due to current flowing in the windings of the transformer, enormous heat is produced. Therefore, transformer is always kept in a tank containing oil. The oil in contact with transformer body heats up, creating convection currents. The warm oil comes in contact with the cooler tank, gives heat to it and descends to the bottom. It again warms up to rise upward. This process is repeated again and again. The heat of the transformer body is thus carried away by convection to the cooler tank. The cooler tank, in turn loses its heat by convection to the surrounding air.
Free or natural convection : When surrounding air comes in contact with a hot body, like air around a burning firewood, the air removes heat from the body by a process called free or natural convection.
- Land and sea breezes in coastal regions (as also trade winds over the Earth) are also formed as a result of free convection currents in air.
Forced convection : The convection process can be accelerated by employing a fan to create a rapid circulation of fresh air. This is called forced convection.
- For example, transformer unit of a desktop computer uses a fan for forced convection.
Radiation:
The transfer of heat energy from one place to another via emission of EM energy (in a straight line with the speed of light) without heating the intervening medium is called radiation.
- Thermal radiation or heat radiation is the radiation produced by the particles of a body by virtue of thermal energy. Hence, every body above absolute zero of temperature gives off thermal radiation.
- The spectrum, i.e., frequency distribution or wavelength distribution, and the intensity for each frequency of thermal radiation is continuous from the far infrared to the extreme ultraviolet region depending on the temperature of the body. In this spectrum, the infrared waves, whose wavelengths range from about 700 nm to about 1 mm, are sensed as heat. When thermal radiations are incident on a body, they increase the molecular motions in the body. Consequently, its temperature rises.
- Thus transfer of heat by radiation is a two-fold process - the conversion of thermal energy into waves and reconversion of waves into thermal energy by the body on which they are incident.
- Since thermal radiation are electromagnetic waves, they have the same speed in free space as that of light, nearly 3 x 108 m/s- This makes radiation the most rapid mode of heat transfer.
Newton’s Laws of Cooling:
Newton's law of cooling : The time rate of fall of temperature of a body is directly
proportional to the excess temperature over the surroundings, provided the excess is small.
If T and T0 are the temperatures of a hot body and the surroundings, respectively, then by Newton's law of cooling, the time rate of fall of temperature of the body, i.e., the time rate of cooling, is
dT/dt ∝ (T − T0)
∴ dT/dt = C(T − T0)
where C is a proportionality constant in a particular case.
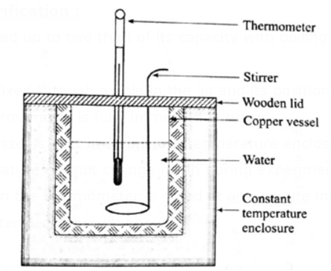
Experimental verification :
- A calorimeter is filled up to two third of its capacity with boiling water and is covered.
- A thermometer is fixed through a hole in the lid and its position is adjusted so that the bulb of the thermometer is fully immersed in water.
- The calorimeter vessel is kept in a constant temperature enclosure or just in open air since room temperature will not change much during experiment.
- The temperature on the thermometer is noted at one minute interval until the temperature of water decreases by about 25 °C.
- A graph of temperature T (along y-axis) is plotted against time t (along x-axis). This graph is called cooling curve (Fig).
- From this graph we can infer how the cooling of hot water depends on the difference of its temperature from that of its surroundings.
- We will also notice that initially the rate of cooling is higher and it decreases as the temperature of the water falls.
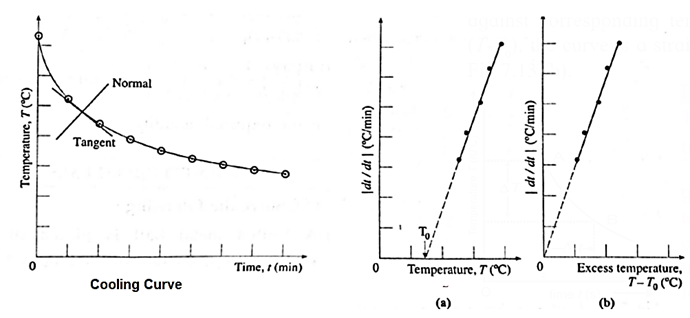
- A tangent is drawn to the curve at suitable points on the curve. The slope of each tangent (dT/dt) gives the rate of fall of temperature at that temperature.
- Taking (0,0) as the origin, if a graph of dT/dt is plotted against corresponding temperature difference (T-T0), the curve is a straight line as shown in Fig (a) and (b).
The above activity shows that a hot body loses heat to its surroundings in the form of heat radiation. The rate of loss of heat depends on the difference in the temperature of the body and its surroundings.
By either graph, we can conclude that
dT/dt ∝ (T − T0)
This verifies Newton's law of cooling.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 6: Mechanical Properties of Solids – Online Notes
Next Chapter : Chapter 8: Sound – Online Notes
We reply to valid query.