Solutions
Practice Set 3.1
Q 1.1 Which of the following sequences are A.P.? If they are A.P. find the common difference.
(1) 2, 4, 6, 8, . . .
Solution :
Here, the first term t1 = 2, t2 = 4, t3 = 6, t4 = 8, ...
t2 – t1 = 4 – 2 = 2,
t3 – t2 = 6 – 4 = 2,
t4 – t3 = 8 – 6 = 2
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is 2.
(2) 2, \(\frac 52\), 3, \(\frac 72\) , . . .
Solution :
Here, the first term t1 = 2, t2 = \(\frac 52\) t3 = 3, t4 = \(\frac 72\), ...
t2 – t1 = \(\frac{5}{2}-2\) = \(\frac{5-4}{2}=\frac{1}{2}\)
t3 – t2 = \(3-\frac 52\) = \(\frac{6-5}{2}=\frac{1}{2}\)
t4 – t3 = \(\frac{7}{2}-3\) = \(\frac{7-6}{2}=\frac{1}{2}\)
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is \(\frac{1}{2}\)
(3) −10, −6, −2, 2, . . .
Solution :
Here, the first term t1= −10, t2 = −6, t3 = −2, t4 = 2,
t2 − t1 = −6 − (−10) = −6 + 10 = 4,
t3 – t2 = –2 – (–6) = −2 + 6 = 4,
t4 – t3 = 2 − (−2) = 2 + 2 = 4.
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is 4.
(4) 0.3, 0.33, .0333, . . .
Solution :
Here, the first term t1 = 0.3, t2 = 0.33, t3 = 0.333,
t2 − t1 = 0.33 − 0,3 = 0.03,
t3 − t2 = 0.333 − 0.33 = 0.003.
The difference between any two consecutive terms is not constant.
Answer is : The given sequence is not an A.P.
(5) 0, —4, —8, —12, . . .
Solution :
Here, the first term t1 = 0, t2 = —4, t3 = —8, t4 = —12,
t2—t1 = —4 – 0 = —4,
t3—t2 = —8 — (—4) = —8 + 4 = —4,
t4—t3 = —12 — (—8)= —12 + 8 = —4.
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is — 4.
(6) \(-\frac{1}{5}\), \(-\frac{1}{5}\), \(-\frac{1}{5}\), . . .
Solution :
Here, the first term t1 = \(-\frac{1}{5}\), t2 = \(-\frac{1}{5}\), t3 = \(-\frac{1}{5}\),
t2—t1 = \(-\frac{1}{5}-(-\frac{1}{5})\) = \(-\frac{1}{5}+\frac{1}{5}\) = 0
t3—t2 = \(-\frac{1}{5}-(-\frac{1}{5})\) = \(-\frac{1}{5}+\frac{1}{5}\) = 0
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is 0.
(7) 3, 3 +\(\sqrt{2}\), 3 + 2\(\sqrt{2}\) , 3 + 3\(\sqrt{2}\) , . . .
Solution :
Here, the first term t1 = 3, t2 = 3 + \(\sqrt{2}\) , t3 = 3 + 2\(\sqrt{2}\) , t4 = 3 + 3\(\sqrt{2}\),
t2—t1 = 3 +\(\sqrt{2}\) – 3 = \(\sqrt{2}\),
t3—t2 = 3 + 2\(\sqrt{2}\) — (3 + \(\sqrt{2}\)) = 3 + 2\(\sqrt{2}\) — 3 —\(\sqrt{2}\) = \(\sqrt{2}\),
t4—t3 = 3 + 3\(\sqrt{2}\) — (3 + 2\(\sqrt{2}\)) = 3 + 3\(\sqrt{2}\) — 3 —2\(\sqrt{2}\) = \(\sqrt{2}\),
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is \(\sqrt{2}\) .
(8) 127, 132, 137, . . .
Solution :
Here, the first term t1 = 127, t2 = 132, t3 = 137,
t2—t1 = 132 — 127 = 5,
t3—t2 = 137 — 132 = 5
The difference between any two consecutive terms is constant.
Answer is : The given sequence is an A.P. The common difference is 5
Q 1.2 Write an A.P. whose first term is a and common difference is d in each of the following.
(1) a = 10, d = 5
Solution :
a = t1 = 10,
t2 = t1 + d = 10 + 5 = 15,
t3 = t2 + d = 15 + 5 = 20,
t4 = t3 + d = 20 + 5 = 25.
Answer is : 10, 15, 20, 25, is the required A.P
(2) a = —3, d = 0
Solution :
a = t1 = —3,
t2 = t1 + d = —3 + 0 = —3,
t3 = t2 + d = —3 + 0 = —3,
t4 = t3 + d = —3 + 0 = —3.
Answer is : —3, —3, —3, —3, …. is the required A.P
(3) a = —7, d = \(\frac{1}{2}\) = 0.5
Solution :
a = t1 = —7,
t2 = t1 + d = —7 + 0.5 = —6.5
t3 = t2 + d = -6.5 + 0.5 = —6,
t4 = t3 + d = —6 + 0.5 = —5.5
Answer is : —7, —6.5, —6, —5.5, … is the required A.P
(4) a = —1.25, d = 3
Solution :
a = t1 = —1.25,
t2 = t1 + d = —1.25 + 3 = 1.75,
t3 = t2 + d = 1.75 + 3 = 4.75,
t4 = t3 + d = 4.75 + 3 = 7.75.
Answer is : —1.25, 1.75, 4.75, 7.75 …. is the required A.P
(5) a = 6, d = —3
Solution :
a = t1 = 6,
t2 = t1 + d = 6 + (—3) = 3,
t3 = t2 + d = 3 + (—3) = 0,
t4 = t3 + d = 0 + (—3) = —3.
Answer is : 6, 3, 0, —3, …. is the required A.P
(6) a = —19, d = —4
Solution :
a = t1 = —19,
t2 = t1 + d = —19 + (—4) = —23,
t3 = t2 + d = —23 + (—4) = —27,
t4 = t3 + d = —27 + (—4) = —31.
Answer is : —19, —23, —27, —31, …. is the required A.P
Q 1.3 : Find the first term and common difference for each of the A.P.
(1) 5, 1, —3, —7, . . .
Solution :
Here, a = t1 = 5, t2 = 1, t3 = — 3, t4 = —7
d = t2 — t1 = 1 — 5 = —4,
d = t3 — t2 = —3 — 1 = —4,
d = t4 — t3 = —7 — (—3) = —7 + 3 = —4,
Answer is : The first term a = 5 and d = — 4.
(2) 0.6, 0.9, 1.2, 1.5, . . .
Solution :
Here, a = t1 = 0.6, t2 = 0.9, t3 = 1.2, t4 = 1.5
d = t2 — t1 = 0.9 — 0.6 = 0.3,
d = t3 — t2 = 1.2 — 0.9 = 0.3,
d = t4 — t3 = 1.5 — 1.2 = 0.3,
Answer is : The first term a = 0.6 and d = 0.3.
(3) 127, 135, 143, 151, . . .
Solution :
Here, a = t1 = 127, t2 = 135, t3 = 143, t4 = 151
d = t2 — t1 = 135 — 127 = 8,
d = t3 — t2 = 143 — 135 = 8,
d = t4 — t3 = 151 — 143 = 8,
Answer is : The first term a = 127 and d = 8.
(4) \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{5}{4}\), \(\frac{7}{4}\), . .
Solution :
Here, a = t1 = \(\frac{1}{4}\), t2 = \(\frac{3}{4}\), t3 = \(\frac{5}{4}\), t4 = \(\frac{7}{4}\)
d = t2 — t1 = \(\frac{3}{4}\)—\(\frac{1}{4}\) = 0.75 — 0.25 = 0.5,
d = t3 — t2 = \(\frac{5}{4}\) — \(\frac{3}{4}\) = 1.25 — 0.75 = 0.5,
d = t4 — t3 = \(\frac{7}{4}\) — \(\frac{5}{4}\) = 1.5 — 1.25 = 0.5,
Answer is : The first term a = \(\frac{1}{4}\) and d = 0.5.
Practice Set 3.2
Q 2.1 : Write the correct number in the given boxes from the following A. P.
(i) 1, 8, 15, 22, . . .
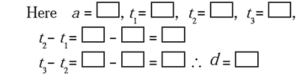
Solution :
(ii) 3, 6, 9, 12, . . .
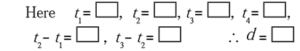
Solution :
(iii) —3, —8, —13, —18, . . .
Solution :
(iv) 70, 60, 50, 40, . . .
Solution :
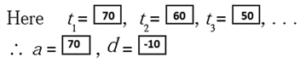
Q 2.2 : Decide whether following sequence is an A.P., if so find the 20th term of the progression.
—12, —5, 2, 9, 16, 23, 30, . . .
Solution :
Here, a = t1 = —12, t2 = —5, t3 =2, t4 = 9, t5 = 16, ...
t2 — t1 = —5 – (—12) = 7,
t3 — t2 = 2 — (—5) = 7,
t4 — t3 = 9 — 2 = 7
t5 — t4 = 16 — 9 = 7
The common difference = d = 7 ... (A constant number)
∴ the given sequence is an A.P.
tn = a + (n — 1)d ... (Formula)
∴ t20 = —12 + (n — 1)d ... (Substituting the values)
= —12 + (20 — 1) × 7
= —12 + (19) × 7
= —12 + 133
∴ t20 = 121
Answer is : The given sequence is an A.P. The 20th term of the A.P. is 121.
Q 2.3 : Given Arithmetic Progression 12, 16, 20, 24, . . . Find the 24th term of this progression.
Solution :
Here, a = t1 = 12, t2 = 16, t3 = 20, t4 = 24, ...
d = t2 — t1 = 16 – 12 = 4
tn = a + (n — 1)d ... (Formula)
t24 = 12 + (24 — 1) × 4 ... (Substituting the values)
= 12 + 23 × 4
= 12 + 92
t24 =104
Answer is : The 24th term is 104.
Q 2.4 : Find the 19th term of the following A.P.
7, 13, 19, 25, . . .
Solution :
Here, a = t1 = 7, t2 = 13, t3 = 19, t4 = 25, ...
d = t2 — t1 = 13 – 7 = 6
tn = a + (n — 1)d ... (Formula)
∴ t19 = 7 + (19 — 1) × 6 ... (Substituting the values)
= 7 + 18 × 6
= 7 + 108
∴ t19 =115
Answer is : The 19th term is 115.
Q 2.5 : Find the 27th term of the following A.P.
9, 4, —1, —6, —11, . . .
Solution :
Here, a = t1 = 9, t2 = 4, t3 = —1, t4 = —6, t5 = —11,...
d = t2 — t1 = 4 – 9 = —5
tn = a + (n — 1)d ... (Formula)
∴ t27 = 9 + (27 — 1) × (—5) ... (Substituting the values)
= 9 + 26 × (—5)
= 9 — 130
∴ t19 = —121
Answer is : The 27th term is 121.
Q 2.6 : Find how many three digit natural numbers are divisible by 5.
Solution :
Three—digit natural numbers divisible by 5 are 100, 105, 110, ... , 995
The smallest and the biggest three—digit natural numbers divisible by 5 are 100 and 995.
Here, a = 100, d = 5, tn = 995.
tn = a + (n — 1)d ... (Formula)
∴ 995 = 100 + (n — 1) × 5 ... (Substituting the values)
995 = 100 + 5n — 5
∴ 5n = 995 – 95 = 900
∴ n = 900/5 = 180
Answer is : There are 180 three—digit natural numbers divisible by 5.
Q 2.7 : The 11th term and the 21st term of an A.P. are 16 and 29 respectively, then find the 41th term of that A.P.
Solution :
t11 = 16 and t21 = 29
Let a be the first term and d the common difference.
∴ tn = a + (n — 1)d ... (Formula)
For 11th term t11 = 16
∴ 16 = a + (11 — 1)d
∴ 16 = a + 10d …..(1)
and t21 = a + (21 — 1)d
∴ 29 = a + 20d …..(2)
Subtracting equation (1) from equation (2).
29 = a + 20d …(2)
16 = a + 10d ....(1)
— — —
——————————————————
13 = 10d
∴ d = 13/10 = 1.3
Substituting d = 1.3 in equation (1),
16 = a + 10 × 1.3
∴ 16 = a + 13
∴ a = 16 – 13 = 3
tn = a + (n — 1)d ... (Formula)
t41 = a + (41 — 1)d = 3 + 40 × 1.3 = 3 + 52
t41 = 55.
Answer is : The 41st term of this A.P. is 55.
Q 2.8 : 11, 8, 5, 2, . . . In this A.P. which term is number —151?
Solution :
Here, a = t1 = 11, t2 = 8, t3 = 5, t4 = 2, ...
d = t2 — t1 = 8 – 11 = —3.
Let the nth term of the given A.P. be —151.
Then tn = —151.
tn = a + (n — 1)d ... (Formula)
∴ —151 = 11 + (n—1) × (—3) ... (Substituting the values)
∴ —151 = 11 + 3 —3n
∴ 3n = 151 + 11 + 3 = 165
∴ n = 165/3 = 55
Answer is : The 55th term of the given A.P. is —151.
Q 2.9 : In the natural numbers from 10 to 250, how many are divisible by 4?
Solution :
The numbers from 10 to 250 which are divisible by 4 are 12, 16, 20, ..., 244, 248.
This is an A.P. with first term a = 12 and d = 4.
Let there be n terms in this A.P.
Then tn =248
tn = a + (n—1)d ... (Formula)
∴ 248 = 12 + (n —1) × 4 ... (Substituting the values)
∴ (n—1) × 4 = 248 — 12
∴ (n—1) × 4 = 236
∴ n – 1 = 236/4 = 59
n = 59 + 1 = 60.
Answer is : 60 numbers from 10 to 250 are divisible by 4.
Q 2.10 : In an A.P. 17th term is 7 more than its 10th term. Find the common difference.
Solution :
Let the first term of the A.P. be a and the common difference d.
tn = a + (n—1)d ... (Formula)
∴ t17 = a + (17 — 1)d ……. (Substituting the values)
∴ t17 = a + 16d …(1)
t10 = a + (10 — 1)d
∴ t10 = a + 9d ….(2)
From the given condition and from (1) and (2),
a +16d = a + 9d + 7
16d —9d = 7
7d = 7 ∴ d = 1
Answer is : The common difference is 1.
Practice Set 3.3
Q 3.1 : First term and common difference of an A.P. are 6 and 3 respectively; find S27.
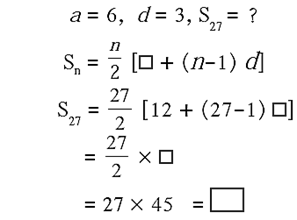
Solution :
Answer is : S27 = 1215
Q 3.2 : Find the sum of first 123 even natural numbers.
Solution :
2, 4, 6, .., 2n are the even natural numbers:
Here, a = t1 = 2, t2 = 4, t3 = 6,
d = t2—t1 = 4 — 2 = 2, n = 123
Sn = \(\frac{n}{2}\)[2a + (n – 1)d] …..(Formula)
∴ Sn = \(\frac{123}{2}\)[2 × 2 + (123— 1) × 2] …..(Substituting the values)
= \(\frac{123}{2}\)(4 + 122 × 2)
= \(\frac{123}{2}\)(4 + 244)
= \(\frac{123}{2}\) × 248
= 123 × 124
∴ Sn = 15252.
Answer is : The sum of the first 123 even natural numbers is 15252.
Q 3.3 : Find the sum of all even numbers between 1 and 350.
Solution :
The even numbers between 1 and 350 are 2, 4, 6, 8, ..., 348.
Here, a = t1=2, d = t2 – t1 = 4—2 = 2, tn = 348.
First we find n.
tn =a + (n — 1)d ….(Formula)
∴ 348 = 2 + (n — 1) × 2 ….(Substituting the values)
∴ 348—2= (n—1) × 2
∴ (n—1) × 2 = 346
∴ n – 1 = 348/2
∴ n—1= 173
∴ n = 173 + 1 = 174
Now, Sn = (t1 + tn)
∴ Sn = \(\frac{n}{2}\)(t1 + tn)
∴ S174 = \(\frac{174}{2}\)(2 + 348)
∴ S174 = \(\frac{174}{2}\)(2 + 348) = 87 × 350 = 30450.
Answer is : The sum of all even numbers between 1 and 350 is 30450.
Q 3.4 : In an A.P. 19th term is 52 and 38th term is 128, find sum of first 56 terms.
Solution :
Let the first term of the AP. be a and common difference d.
t19 = 52 and t33 = 128 ….(Given)
tn = a + (n — 1)d ……(Formula)
∴ t19 = a + (19 — 1)d
∴ t19 = a + 18d = 52 ….(Given, t19 = 52) …..(1)
and t38 = a + (38 — 1)d
t38 = a + 37d = 128 (Given, t38 = 128) …….(2)
Adding equations (1) and (2),
a + 18d = 52 …....(1)
a + 37d = 128 …...(2)
—————————————————
2a + 55d = 180 …..(3)
Now, Sn = \(\frac{n}{2}\)[2a + (n – 1)d] …..(Formula)
∴ S56 = \(\frac{56}{2}\)[2a + (56 — 1)d]
= 28(2a + 55d)
= 28 × 180 ….[From (3)1
∴ S56 = 5040.
Answer is : The sum of the first 56 terms is 5040.
Q 3.5 : Complete the following activity to find the sum of natural numbers between 1 and 140 which are divisible by 4.
Solution :
Between 1 and 140, natural numbers divisible by 4
4, 8, . . . . . . . . , 136
tn = 136, a = 4, d = 4
tn = a + (n — 1)d
136 = 4 + (n — 1) × 4
|
[ (n — 1) × 4 = 136 — 4 = 132 n — 1 = 132/4 = 33 n = 33 + 1 = 34] |
n = 34 → Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
S34 = \(\frac{34}{2}\)[2 × 4 + (34 – 1) × 4] = 2380
Sum of numbers from 1 to 140, which are divisible by 4 = 2380
Q 3.6 : Sum of first 55 terms in an A.P. is 3300, find its 28th term.
Solution :
Sn = S55 = 3300.
Let the first term of the A.P. be a and the common difference d.
Sn = \(\frac{n}{2}\)[2a + (n — 1)d] …..(Formula)
∴ S55 = \(\frac{55}{2}\)[2a +(55 — 1)d] = \(\frac{55}{2}\)[2a + 54d]
∴ S55 = \(\frac{n}{2}\) × 2(a + 27d)
∴ 3300 = 55 (a + 27d) ….(Given : S55 = 3300)
\(\frac{3300}{55}\) = a + 27d ….(Dividing both sides by 55)
∴ 60 = a + 27d …….(1)
Now, the 28th term is t28
tn = a + (n — 1)d …..(Formula)
∴ t28 = a + (28 — 1)d
= a + 27d.
But, a + 27d = 60 ….[From (1)]
∴ t28 = 60
Answer is : The 28th term is 60.
Q 3.7 : In an A.P. sum of three consecutive terms is 27 and their product is 504, find the terms. (Assume that three consecutive terms in A.P. are a — d , a, a + d.)
Solution :
Let the three consecutive terms in an A.P. be a –d, a and a+d.
From the first condition,
(a—d) + a + (a+d) = 27
A — d + a + a + d = 27
∴ 3a = 27
∴ a = 9
From the second condition,
(a — d) × a × (a + d) = 504
∴ (9 — d) × 9 × (9 + d) = 504 …..(Substituting a = 9)
∴ (9 — d)(9 + d) = 504/9 = 56
81 – d2 = 56
∴ 81—56 = d2
∴ d2 = 25 ∴ d = ±5
When d = 5, the three consecutive terms are
a – d = 9—5 = 4, a = 9, a + d = 9 + 5 = 14
When d = — 5, the three consecutive terms are
a—d = 9— (—5) = 9 + 5 = 14, a = 9, a + d = 9 + (—5) = 9 – 5 = 4.
Answer is : The three consecutive terms are 4, 9, 14 or 14, 9, 4.
Q 3.8 : Find four consecutive terms in an A.P. whose sum is 12 and sum of 3rd and 4th term is 14. (Assume the four consecutive terms in A.P. are a — d , a, a + d, a + 2d.)
Solution :
Let the four consecutive terms in an A.P. be a — d, a, a + d and a + 2d.
From the first condition,
(a — d) + a + (a+d) + (a + 2d) = 12
∴ a – d + a + a + d + a + 2d = 12
∴ 4a + 2d = 12
∴ 2a + d = 6 .. (Dividing both the sides by 2) ... (1)
From the second condition,
(a + d) + (a + 2d) = 14
∴ a + d + a + 2d=14
∴ 2a + 3d = 14 ….. (2)
2a + d + 2d = 14
Substituting 2a+ d= 6 from eq.(1)
6 + 2d = 14
2d = 14 — 6 = 8
∴ d = 8/2 = 4
Substituting d = 4 in equation (1),
2a + 4 = 6, ∴ 2a = 6 – 4 = 2
∴ a = 1
Taking a = 1 and d = 4
First term = a — d = 1 – 4 = —3
Second term = a = 1
Third term = a + d = 1 + 4 = 5
Fourth term = a + 2d = 1 + 2(4) = 1 + 8 = 9
Answer is : The four consecutive terms are — 3, 1, 5 and 9.
Q 3.9 : If the 9th term of an A.P. is zero then show that the 29th term is twice the 19th term.
Solution :
Proof : Let the first term of the A.P. be a and the common difference d. t9 = 0
tn = a + (n — 1)d ...(Formula)
∴ t9 = a + (9 – 1)d = 0
∴ a + 8d = 0
∴ a = —8d .. (1)
For 19th term,
t19 = a + (19 – 1)d = a + 18d
=—8d + 18d .. [From (1)]
∴ t19 = 10d …(2)
For 29th term,
t29 = a + (29 — 1)d = a + 28d
= —8d + 28d .... [From (1)]
∴ t29 = 20d ….(3)
From (3) and (2),
t29 = 20d = 2 x 10d =2 × t19
∴ 29th term is twice the 19th term.
Practice Set 3.4
Q 4.1 : On 1st Jan 2016, Sanika decides to save ₹ 10, ₹ 11 on second day, ₹ 12 on third day. If she decides to save like this, then on 31st Dec 2016 what would be her total saving?
Solution :
Sanika saves ₹ 10 on the first day, ₹ 11 on the second day, ₹ 12 on the third day,
10, 11, 12, is a sequence.
The common difference d = 11 — 10 = 12 — 11 = 1
which is constant.
10, 11, 12, is an A.P.
Here, a = 10 and d = 1.
The year 2016 was a leap year.
A leap year has 366 days. n = 366.
The total savings in 366 days is S366
Sn = \(\frac{n}{2}\)[2a + (n — 1)d] …..(Formula)
∴ S366 = \(\frac{366}{2}\)[2 × 10 + (366— 1) × 1] … (Substituting the values)
= 183(20 + 365)
= 183 × 385
S366 = 70455.
Answer is : Sanika’s total savings would be ₹ 70,455.
Q 4.2 : A man borrows ₹ 8000 and agrees to repay with a total interest of ₹ 1360 in 12 monthly instalments. Each instalment being less than the preceding one by ₹ 40. Find the amount of the first and last instalment.
Solution :
The amount repaid = ₹ 8000 + ₹ 1360 = ₹ 9360
The number of instalments = 12
n = 12, Sn = S12 = 9360
Each instalment is ₹ 40 less than the preceding one.
d = —40.
Let the first instalment be ₹ a. This is an A.P.
Sn = \(\frac{n}{2}\)[2a +(n — 1)d] …. (Formula)
∴ S12 = 9360 = \(\frac{12}{2}\)[2a + (12 — 1) × ( — 40)] ….. (Substituting the values)
9360 = 6[2a + (11) × (—40)]
9360 = 6(2a — 440)
6(2a — 440) = 9360
2a — 440 = 9360/6 …..(Dividing both the sides by 6)
2a — 440 = 1560
2a = 1560 + 440 ∴ 2a = 2000 ∴ a = 1000
The last instalment = tn
tn = a + (n — 1)d …. (Formula)
t12 = 1000 + (12 — 1) × (—40)
= 1000 + 11 × (—40)
= 1000 — 440
t12 = 560.
Ans. The first instalment is ₹ 1000 and the last instalment is ₹ 560.
Q 4.3 : Sachin invested in a national saving certificate scheme. In the first year he invested ₹ 5000, in the second year ₹ 7000, in the third year ₹ 9000 and so on. Find the total amount that he invested in 12 years.
Solution :
The amount invested by Sachin : ₹ 5,000, ₹ 7000, ₹ 9000. This is a sequence with common difference d = 2000.
∴ this is an A_P.
Here, a = 5000, d = 2000, n = 12.
We want to find S12.
Sn = \(\frac{n}{2}\)[2a + (n — 1)d] ……(Formula)
S12 = \(\frac{12}{2}\)[2 × 5000+ (12— 1) × 2000] …..(Substituting the values)
= 6[10000 + 11 × 2000]
= 6[10000 + 22000]
= 6 × 32000
∴ S12 = 192000
Answer is : Sachin invested ₹ 1,92,000 in 12 years
Q 4.4 : There is an auditorium with 27 rows of seats. There are 20 seats in the first row, 22 seats in the second row, 24 seats in the third row and so on. Find the number of seats in the 15th row and also find how many total seats are there in the auditorium?
Solution :
20 seats in the first row, 22 seats in the second row, 24 seats in the third row.
20, 22, 24, is a sequence.
The number of seats increasing in consecutive rows
= 24 — 22 = 22 – 20 = 2
∴ d = 2
There are 20 seats in the first row.
∴ a = 20
20, 22, 24, is an A.P.
We have to find the number of seats in the 15th row.
i.e. t15.
tn = a + (n—1)d ...(Formula)
∴ t15 = 20 + (15 — 1) × 2 …..(Substituting the values)
= 20 + 14 × 2 = 20 + 28
∴ t15 = 48
Total number of seats in 27 rows, i.e. we have to find S27.
Sn = \(\frac{n}{2}\)[2a + (n — 1)d] ……(Formula)
∴ S27 = \(\frac{27}{2}\)[2 × 20 + (27 — 1) × 2] …. (Substituting the values)
= \(\frac{27}{2}\)[40 + 26 × 21]
= \(\frac{27}{2}\)[40 + 52]
= \(\frac{27}{2}\) × 92 = 27 × 46
∴ S27 = 1242
Answers is : There are 46 seats in the 15th row. The total number of seats in the auditorium is 1242.
Q 4.5 : Kargil’s temperature was recorded in a week from Monday to Saturday. All readings were in A.P. The sum of temperatures of Monday and Saturday was 5° C more than sum of temperatures of Tuesday and Saturday. If temperature of Wednesday was —30° celsius then find the temperature on the other five days.
Solution :
The temperatures are in A.P. (Given)
Let the temperatures, in °C, from Monday to Saturday be a — 3d, a — 2d, a—d, a, a + d and a + 2d respectively.
The temperature on Wednesday is — 30 °C. i.e. a — d = —30 ….(Given) ….(1)
The sum of the temperatures on Monday and Saturday = the sum of the temperatures on Tuesday and Saturday +5 °C.
∴ (a—3d) + (a + 2d) = (a—2d) + (a + 2d) + 5
a—3d = a—2d + 5
— 3d + 2d = 5
—d = 5
d = —5 ……(2)
Substituting d = —5 in equation (1),
a — ( —5) = — 30
a + 5 = —30
a = —30 — 5
a = —35 ….(3)
Substituting the values of a and d from (3) and (2),
a — 3d = —35 — 3(—5)= —35 + 15 = —20.
a—2d = —35—2(—5) = —35 + 10 = —25,
a—d = —30, …..[From(l)]
a = — 35 ……[From (3)]
a + d = —35 + (—5) = —35 – 5 = —40
a + 2d = —35 + 2(—5) = —35—10 = —45
Answer is : The temperature at Kargil for the week were —20 °C, —25 °C, —30 °C, —35 °C, — 40 °C, — 45 °C respectively.
Q 4.6 : On the world environment day tree plantation programme was arranged on a land which is triangular in shape. Trees are planted such that in the first row there is one tree, in the second row there are two trees, in the third row three trees and so on. Find the total number of trees in the 25 rows.
Solution :
The number of trees increases by 1 in consecutive rows. d = 1.
There is one tree in the first row. a = 1. This is an A.P.
There are 25 rows. n = 25.
So, we have to find the total number of trees in 25 rows.
It means, we have to find S25.
Sn = \(\frac{n}{2}\)[2a + (n — 1)d] ……(Formula)
S25 = \(\frac{25}{2}\)[2 × 1 + (25 — 1) × 1] …..(Substituting the values)
= \(\frac{25}{2}\)[2 + 24 × 1]
= \(\frac{25}{2}\)[26] = 25 × 13
∴ S25 = 325
Answer is : Total number of trees are 325.
We reply to valid query.