Mathematical Methods
Maharashtra Board-Class-11-Science-Physics-Chapter-2
Notes-Part-2
Topics to be Learn : Part-2
|
Resolution of vectors :
The process of splitting a given vector into its components is called resolution of the vector. The components can be found along directions at any required angles, but if these components are found along the directions which are mutually perpendicular, they are called rectangular components.
Component and the component vector (or vector component) :
Let \(\vec{A}\) be the given vector and \(\hat{u}\) be the unit vector specifying the given direction along a line l, Fig.

- Let \(\vec{A}\) make an angle θ with the direction of \(\hat{u}\).
- The vector \(\vec{A}\) is moved parallel to itself so that its tail lies on the line l. A perpendicular is dropped from the tip of onto the line l.
- The projection of \(\vec{A}\) on the line, OP = A cos θ is called the scalar component (or simply component) of \(\vec{A}\) along the line.
Resolution of a vector :
The resolution of a vector into components is equivalent to replacing the original vector with the sum of two or three component vectors.
In general, we choose the set of three vectors such that one vector is parallel to the x-axis, the second parallel to the y-axis and the third parallel to the z-axis.
Given a vector \(\vec{A}\), its components along the Cartesian coordinate axes, x, y and z, are called its Cartesian or rectangular components and are labelled Ax, Ay and Az respectively. The component vector Ax\(\hat{i}\) is parallel to the x-axis with magnitude Ax , Ay\(\hat{j}\) is parallel to the y-axis with magnitude Ay and Az\(\hat{k}\) is parallel to the z-axis with magnitude Az. For a given vector \(\vec{A}\) (or a set of coplanar vectors), the Cartesian coordinate axes may be conveniently so oriented that \(\vec{A}\) lies in the xy plane. In Fig \(\vec{OR}\) = \(\vec{A}\), \(\vec{OP}\) = Ax\(\hat{i}\), \(\vec{OQ}\) = \(\vec{PR}\) = Ay\(\hat{j}\) Since \(\vec{OR}\) = \(\vec{OP}\) + \(\vec{PR}\) ∴ \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) The magnitude of (\vec{A}\) is, by Pythagorus' theorem, A = \(\sqrt{A_x^2+A_y^2}\) Also, if θ is the angle made by \(\vec{A}\) with the positive x-axis, Ax = OP = A cos θ and Ay = PR = A sin θ so that, its direction with respect to the positive x-axis specified by the angle θ is found from tan θ = Ay/Ax . When there are noncoplanar vectors, it becomes necessary to use the third dimension as well. In general, therefore, ∴ \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\) The magnitude of \(\vec{A}\) is A = \(\sqrt{A_x^2+A_y^2 +A_z^2}\) In above Fig. OP is the projection of \(\vec{A}\) onto the xy plane. If A makes angles, α, β and γ respectively with the x, y and z—axes, then, cos α = Ax/A, cos β = Ay/A, and cos γ = Az/A These are called the direction cosines of \(\vec{A}\).


Multiplication of Vectors:
Two ways of multiplying two vectors :
Two vectors can be multiplied together in two different ways : One resulting in a scalar and the other in a vector. The first is called the scalar product (denoted by a dot, . , between the two vectors being multiplied) while the second is called the vector product (denoted by a cross ‘x’ between the two vectors).
Accordingly, the scalar product is also called a dot product and the vector product is called a cross product.
- It means when we multiply vectors of the same or different types, we get a new physical quantity which may either be a scalar (scalar product) or a vector (vector product).
- Multiplication of a scalar with a scalar is always a scalar
- Multiplication of scalar with a vector is always a vector.
Note : When handling vectors, the usual symbol of multiplication, x , is given a different meaning, that of a vector product. Hence, care must be taken to use the proper symbol of multiplication, a . or a x.
Scalar Product (Dot Product): The scalar product or dot product of two nonzero vectors \(\vec{A}\) and \(\vec{B}\) is defined as the product of magnitudes of the two vectors and the cosine of the angle θ between the two vectors. The scalar product of \(\vec{A}\) and \(\vec{B}\) is written as \(\vec{A}\).\(\vec{B}\), . ( \(\vec{A}\) dot \(\vec{B}\) ) \(\vec{A}\).\(\vec{B}\) = AB cos θ, where θ is the angle between and
Q. Show that scalar product of two vectors is commutative :
(a) B cos θ is the component of \(\vec{B}\) in the direction of \(\vec{A}\) (b) A cos θ IS the component of \(\vec{A}\) in the direction of \(\vec{B}\) Since, the order in which scalar quantities are written is immaterial, it follows that \(\vec{A}\).\(\vec{B}\) = AB cos θ = A(B cos θ) = B (A cos θ) = \(\vec{B}\).\(\vec{A}\) that is, the scalar product of two vectors is commutative; as shown in Fig., the choice of the interpretation is left to the physics of the situation.

Test for perpendicularity of two non-zero vectors :
Let \(\vec{A}\) and \(\vec{B}\) be two non-zero vectors. If they are perpendicular to each other, the angle between them, θ = 90° and cos 90° = 0.
\(\vec{A}\).\(\vec{B}\) = AB cos θ = AB (cos 90°) = 0
Thus, the test for perpendicularity of two non-zero vectors is that their scalar product must be zero.
If follows that if \(\vec{A}\).\(\vec{B}\) = 0 with A ≠ 0 and B ≠ 0, then the vectors are perpendicular to each other.
If two vectors are parallel : Let the vectors \(\vec{A}\) and \(\vec{B}\) be parallel to each other, i.e., the angle between them, θ = 0° and cos 0° = 1.
\(\vec{A}\).\(\vec{B}\) = AB cos 0° = AB (1) = AB
Thus, the maximum value of the dot product of two vectors is obtained when the two vectors are parallel.
If two vectors are antiparallel : Let the vectors \(\vec{A}\) and \(\vec{B}\) be antiparallel (opposite in direction) to each other, i.e., the angle between them, θ = 180° and
cos 180° = −1.
\(\vec{A}\).\(\vec{B}\) = AB cos 180° = AB(−1) = − AB.
If two vectors are equal to each other : Let the vectors (\vec{A}\) and \(\vec{B}\) , be two equal vectors,
i.e., (\vec{A}\) = \(\vec{B}\) Then, A = B, and the angle between them, θ = 0° and cos 0° = 1.
∴ \(\vec{A}\).\(\vec{B}\) = \(\vec{A}\).\(\vec{A}\) = AA = A2 = B2 or, the scalar product of a vector with itself equals the square of its magnitude.
Expression for the scalar product of two vectors in terms of their rectangular components : Let the two vectors be \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\) and \(\vec{B}\) = Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\). The unit vectors \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) being mutually perpendicular, \(\hat{i}\).\(\hat{j}\) = \(\hat{j}\).\(\hat{k}\) = \(\hat{k}\).\(\hat{i}\) = (1)(1) cos 90° = 0 and \(\hat{i}\).\(\hat{i}\) = \(\hat{j}\).\(\hat{j}\) = \(\hat{k}\).\(\hat{k}\) = (1)(1) cos 0° = 1 Therefore, \(\vec{A}\).\(\vec{B}\) = (Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\)).(Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\)) = AxBx ( \(\hat{i}\).\(\hat{i}\) ) + AxBy ( \(\hat{i}\).\(\hat{j}\) ) + AxBz ( \(\hat{i}\).\(\hat{k}\) ) + AyBx (\(\hat{j}\).\(\hat{i}\)) + AyBy ( \(\hat{j}\).\(\hat{j}\) ) + AyBz ( \(\hat{j}\).\(\hat{k}\) ) + AzBx ( \(\hat{k}\).\(\hat{i}\) ) + AzBy ( \(\hat{k}\).\(\hat{j}\) ) + AzBz ( \(\hat{k}\).\(\hat{k}\) ) = AxBx(1) + AxBy(0) + AxBz(0) + AyBx(0) + AyBy(1) + AyBz(0) + AzBx(0) + AzBy(0) + AzBz(1) = AxBx + AyBy + AzBz
Characteristics (properties) of scalar product : (1) Scalar product of two vectors is commutative : \(\vec{A}\).\(\vec{B}\) = \(\vec{B}\).\(\vec{A}\) (2) Scalar product is distributive over vector addition : \(\vec{A}\).\(\vec{B}\) + \(\vec{C}\) = \(\vec{A}\).\(\vec{B}\) + \(\vec{A}\).\(\vec{C}\) (3) For two parallel vectors \(\vec{A}\) and \(\vec{B}\) (θ = 0°), \(\vec{A}\).\(\vec{B}\) = AB so that \(\vec{A}\).\(\vec{A}\) = A2 or A = \(\sqrt{\vec{A}.\vec{A}}\) i.e., the magnitude of a vector is the square root of the scalar product of the vector with itself. (4) For two antiparallel vectors \(\vec{A}\) and \(\vec{B}\) (θ = 180°), \(\vec{A}\).\(\vec{B}\) = −AB (5) If \(\vec{A}\).\(\vec{B}\) = 0, then either A = 0 or B = 0 or θ = 90°. Thus, if the scalar product of two non-zero vectors is zero then they are perpendicular to each other. (6) If \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\) and (\vec{B}\) = Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\). \(\vec{A}\).\(\vec{B}\) = AxBx + AyBy + AzBz Also from property (4) above, A = \(\sqrt{A_x^2 + A_y^2 + A_z^2}\) and B = \(\sqrt{B_x^2 + B_y^2 + B_z^2}\) ∴ cos θ = \(\frac{\vec{A}.\vec{B}}{AB} = \frac{A_xB_x + A_yB_y + A_zB_z}{(\sqrt{A_x^2 + A_y^2 + A_z^2})(\sqrt{B_x^2 + B_y^2 + B_z^2})}\) (7) If \(\vec{A}\).\(\vec{B}\) = \(\vec{A}\).\(\vec{C}\), where \(\vec{A}\) ≠ 0 then \(\vec{B}\) is not necessarily equal to \(\vec{C}\). Justification : Let \(\vec{A}\).\(\vec{B}\) = \(\vec{A}\).\(\vec{C}\), where \(\vec{A}\) ≠ 0 By the definition of an additive inverse, \(\vec{A}\).\(\vec{B}\) − \(\vec{A}\).\(\vec{C}\) = \(\vec{A}\).\(\vec{C}\) − \(\vec{A}\).\(\vec{C}\) = 0 Then, by the distributive law, \(\vec{A}\).(\(\vec{B}\) − \(\vec{C}\)) = 0 Therefore, since \(\vec{A}\) ≠ 0, there are two possibilities : (i) \(\vec{B}\) − \(\vec{C}\) = 0 i.e., \(\vec{B}\) = \(\vec{C}\) or (ii) \(\vec{A}\) is perpendicular to \(\vec{B}\) − \(\vec{C}\) Or, if \(\vec{B}\) ⊥ \(\vec{C}\) and \(\vec{C}\) ⊥ \(\vec{A}\) Then \(\vec{A}\).\(\vec{B}\) = 0 = \(\vec{A}\).\(\vec{C}\) That is, it does not necessarily follow that \(\vec{B}\) = \(\vec{C}\)
Vector Product (cross product):
The vector or cross product of two vectors, is a vector whose magnitude is equal to the product of their magnitudes and the sine of the smaller angle between them. Its direction is perpendicular to the plane of the origin, vectors, in the sense of advancement of a right-handed screw rotated from the first vector in the product to the second through the smaller angle between them.
The vector product of \(\vec{A}\) and \(\vec{B}\) is denoted by \(\vec{A}\) x \(\vec{B}\) (read as \(\vec{A}\) cross ), and if θ is the smaller angle between them,
\(\vec{A}\) x \(\vec{B}\) = (AB sin θ)
where the unit vector \(\hat{u}\) (and, \(\vec{A}\) x \(\vec{B}\) ) has a direction given by treating ,\(\vec{A}\), \(\vec{B}\) and \(\hat{u}\) as a right-handed system : If a right-handed screw is placed perpendicular to and \(\vec{A}\) and \(\vec{B}\) a rotation of \(\vec{A}\) into \(\vec{B}\) moves the screw in the direction of \(\hat{u}\) Fig. (a)

- (a) \(\vec{A}\) x \(\vec{B}\) is perpendicular to both and such that \(\vec{A}\), \(\vec{B}\) and \(\vec{A}\) x \(\vec{B}\) form a right-handed system
- (b) | \(\vec{A}\) x \(\vec{B}\) | is the product of the magnitude of and the component of perpendicular to
- (c) | \(\vec{A}\) x \(\vec{B}\) | is also the product of the magnitude of B and the component of perpendicular to
Characteristics of Vector Product: (1) Vector product does not obey commutative law of multiplication. \(\vec{A}\) x \(\vec{B}\) = −\(\vec{B}\) x \(\vec{A}\) ∴ \(\vec{A}\) x \(\vec{B}\) ≠ \(\vec{B}\) x \(\vec{A}\) Explanation : Let θ be the smaller angle between \(\vec{A}\) and \(\vec{B}\) . The magnitude of \(\vec{A}\) x \(\vec{B}\) is AB sin θ while its direction is such that , \(\vec{A}\), and ( \(\vec{A}\) x \(\vec{B}\) ) form a right-handed system : If a right-handed screw is placed perpendicular to \(\vec{A}\) and \(\vec{B}\) , a rotation of \(\vec{A}\) into \(\vec{B}\) moves the screw in the direction of \(\vec{C}\) = \(\vec{A}\) x \(\vec{B}\) , as shown in Fig.(a) On the other hand, the magnitude of \(\vec{B}\) x \(\vec{A}\) is also AB sin θ, but its direction is such that now \(\vec{B}\), \(\vec{A}\) , and ( \(\vec{B}\) x \(\vec{A}\) ) form a right-handed system : If a right-handed screw is placed perpendicular to \(\vec{A}\) and \(\vec{B}\) , a rotation of \(\vec{B}\) into \(\vec{A}\) moves the screw in the direction of \(\vec{D}\) = \(\vec{B}\) x \(\vec{A}\), as shown in Fig.(b) Since C = D = AB sin θ, the vectors ( \(\vec{A}\) x \(\vec{B}\) ) and ( \(\vec{B}\) x \(\vec{A}\) ) are equal in magnitude but, as is clear from the diagrams, are opposite in direction. ∴ \(\vec{A}\) x \(\vec{B}\) = − \(\vec{B}\) x \(\vec{A}\) Thus \(\vec{A}\) x \(\vec{B}\) ≠ \(\vec{B}\) x \(\vec{A}\) Thus, the vector product of two vectors is not commutative. (2) Vector product is distributive over vector addition: \(\vec{A}\) x ( \(\vec{B}\) + \(\vec{C}\) ) = \(\vec{A}\) x \(\vec{B}\) + \(\vec{A}\) x \(\vec{C}\) .. (Left distributive law) ( \(\vec{B}\) + \(\vec{C}\) ) x \(\vec{A}\) = \(\vec{B}\) x \(\vec{A}\) + \(\vec{C}\) x \(\vec{A}\) (Right distributive law) (3) \(\vec{A}\) x \(\vec{B}\) represents the area vector of the parallelogram whose adjacent sides represent the coinitial vectors \(\vec{A}\) and \(\vec{B}\) This is the geometrical interpretation of \(\vec{A}\) x \(\vec{B}\) . (4) Vector product of a vector with itself is a zero vector. (5) If the vector product of two non-zero vectors is a zero vector then they are collinear, i.e., parallel or antiparallel. Explanation : Let (\vec{A}\) and \(\vec{B}\) be two non-zero vectors : A ≠ 0 and B ≠ 0. If they are parallel or antiparallel, the angle between them, θ = 0° or 180° respectively and sin 0° = sin 180° = 0. ∴ | \(\vec{A}\) x \(\vec{B}\) | = AB sin θ = AB(0) = 0 ∴ \(\vec{A}\) x \(\vec{B}\) = 0 Thus, the test for coalignment, i.e., parallel or antiparallel alignment, of two non-zero vectors is that their vector product must be a zero vector. It follows that if \(\vec{A}\) x \(\vec{B}\) = 0 with A ≠ 0 and B ≠ 0, then the vectors must be parallel or antiparallel. (6) If \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\) and \(\vec{B}\) = Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\). \(\vec{A}\) x \(\vec{B}\) = (AyBz − AzBy)\(\hat{i}\) + (AzBx − AxBz)\(\hat{j}\) + (AxBy − AyBx)\(\hat{k}\) = \(\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z\\ B_x & B_y & B_z \end{vmatrix}\) (7) sin θ = \(\frac{|\vec{A}x\vec{B}|}{AB}\) Where A = \(\sqrt{A_x^2 + A_y^2 + A_z^2}\) and B = \(\sqrt{B_x^2 + B_y^2 + B_z^2}\) And | \(\vec{A}\) x \(\vec{B}\) | = [(AyBz − AzBy)2 + (AzBx − AxBz)2 + (AxBy − AyBx)2 ]1/2

Expression for the cross product of two vectors in terms of their rectangular (Cartesian) components and express it in the determinant form :
Let the two vectors be \(\vec{A}\) = Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\) and \(\vec{B}\) = Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\).
The unit vectors \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) being mutually perpendicular,
| \(\hat{i}\) x \(\hat{j}\) | = | \(\hat{j}\) x \(\hat{k}\) | = | \(\hat{k}\) x \(\hat{i}\) | = (1)(1) sin 90° = 1 and
\(\hat{i}\) x \(\hat{j}\) = \(\hat{k}\), \(\hat{j}\) x \(\hat{k}\) = \(\hat{i}\), \(\hat{k}\) x \(\hat{i}\) = \(\hat{j}\),
Since \(\hat{j}\) x \(\hat{i}\) = −\(\hat{i}\) x \(\hat{j}\) and so on \(\hat{j}\) x \(\hat{i}\) = −\(\hat{k}\), \(\hat{k}\) x \(\hat{j}\) = −\(\hat{i}\) and \(\hat{i}\) x \(\hat{k}\) = −\(\hat{j}\)
Also,
| \(\hat{i}\) x \(\hat{i}\) | = | \(\hat{j}\) x \(\hat{j}\) | = | \(\hat{k}\) x \(\hat{k}\) | = (1)(1) sin 0° = 0
Therefore, \(\vec{A}\) x \(\vec{B}\)
= (Ax\(\hat{i}\) + Ay\(\hat{j}\) + Az\(\hat{k}\)) x (Bx\(\hat{i}\) + By\(\hat{j}\) + Bz\(\hat{k}\).)
= AxBx (\(\hat{i}\) x \(\hat{i}\)) + AxBy (\(\hat{i}\) x \(\hat{j}\)) + AxBz (\(\hat{i}\) x \(\hat{k}\)) + AyBx (\(\hat{j}\) x \(\hat{i}\)) + AyBy ( \(\hat{j}\) x \(\hat{j}\)) + AyBz ( \(\hat{j}\) x \(\hat{k}\)) + AzBx (\(\hat{k}\) x \(\hat{i}\)) + AzBy (\(\hat{k}\) x \(\hat{j}\)) + AzBz ( \(\hat{k}\) x \(\hat{k}\))
= AxBx(1) + AxBy(\(\hat{k}\)) + AxBz(-\(\hat{j}\)) + AyBx(-\(\hat{k}\)) + AyBy(0) + AyBz(\(\hat{i}\)) + AzBx(\(\hat{j}\)) + AzBy(-\(\hat{i}\)) + AzBz(0)
= (AyBz − AzBy)\(\hat{i}\) + (AzBx − AxBz)\(\hat{j}\) + (AxBy − AyBx)\(\hat{k}\)
Using the determinant notation, the cross product of \(\vec{A}\) and \(\vec{B}\) is written as
\(\vec{A}\) x \(\vec{B}\) = \(\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z\\ B_x & B_y & B_z \end{vmatrix}\)
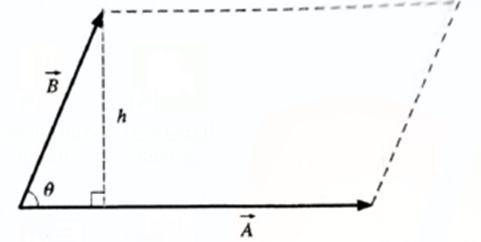
Q. Show that the magnitude of the vector product of two vectors is numerically equal to the area of the parallelogram formed by the two vectors as its adjacent sides with the common tail.
Let \(\vec{A}\) and \(\vec{B}\) represent two adjacent sides of a parallelogram as shown in Fig. Let θ be the smaller angle between the two vectors and h be the height of the parallelogram. In the diagram, the base of the parallelogram is |\(\vec{A}\)| = A, and h = B sin θ. Area of the parallelogram = base x height = |\(\vec{A}\)| h = AB Sin θ = | \(\vec{A}\) x \(\vec{B}\) | That is, the magnitude of the vector product of two vectors gives the area of a parallelogram formed by the two vectors as its adjacent sides.
Distinguish between the scalar / dot product and vector/ cross product : product of the two vectors, in the sense of advancement of a right-handed screw rotated from the first vector in the product to the second through the smaller angle between them.
Scalar product
Vector product
A scalar product is equal to the product of the magnitudes of the two vectors and the cosine of the angle between them.
The magnitude of a vector product is equal to the product of the magnitudes of the two vectors and the sine of the smaller angle between them.
It has no direction
Its direction is perpendicular to the
It is commutative
It is not commutative
It is zero if the two vectors are perpendicular to each other.
It is zero if the two vectors are parallel or antiparallel.
The self dot product of a vector is equal to the square of its magnitude.
The self cross product of a vector is a zero vector.
It is maximum when the two vectors are parallel.
Its magnitude is maximum when the two vectors are perpendicular to each other.
Introduction to Differential and Integral Calculus :
Calculus is the study of continuous (not discrete) changes in mathematical quantities. Here we will learn the basics of the two branches of calculus namely differential and integral calculus.
Derivative of a function : Consider a quantity y whose value depends upon a single variable x, as expressed by an equation defining y as some specific function of x :
y = f(x)
Here, x is called the independent variable and y is called the dependent variable.
Suppose the variable x is given an increment Δx from x = x0, that is, if x changes from x = x0 to x = x0 + Δx , so that the function f (x) is thereby given an increment Δy = f(x0 + Δx) —f(x0) from y = f(x0). Then, the quotient
\(\frac{Δy}{Δx}=\frac{\text{change in y}}{\text{change in x}}\)
is called the average rate of change of the function on the interval between x = x0 to x = x0 + Δx.
The derivative of the function y = f (x) with respect to x at the point x = x0 is defined as
\(\lim\limits_{Δx\to 0} \frac{dy}{dx}=\lim\limits_{Δx\to 0}\frac{f(x_0+Δx)-f(x_0)}{Δx}\) provided the limit exists.
This limit, the derivative, is called the instantaneous rate of change (or simply, the rate of change) of the function y = f(x) with respect to x at x = x0.
It is customary to drop the subscript 0 and write the derivative of y = f(x) with respect to x as
\(\lim\limits_{Δx\to 0}\frac{dy}{dx}=\lim\limits_{Δx\to 0}\frac{f(x+Δx)-f(x)}{Δx}\)
and indicate it as or f’(x). The process of finding the derivative is called differentiation.
Properties of differentiation: Let f1(x) and f2(x) be two different functions of x and let s be a constant. (i) \(\frac{d(sf(x)}{dx}=s\frac{df(x)}{dx}\) (ii) \(\frac{d}{dx}\)(f1(x) + f2(x)) = \(\frac{df_1(x)}{dx}+\frac{df_2(x)}{dx}\) (iii) \(\frac{d}{dx}\)(f1(x) x f2(x)) = \(f_1(x)\frac{df_2(x)}{dx}+f_2(x)\frac{df_1(x)}{dx}\) (iv) \(\frac{d}{dx}[\frac{f_1(x)}{f_2(x)}]\)= \(\frac{1}{f_2(x)}\frac{df_1(x)}{dx}-\frac{f_1(x)}{f_2^2(x)}\frac{df_2(x)}{dx}\) (v) If x depends on time another variable t then, \(\frac{df(x)}{dt}\)=\(\frac{df(x)}{dx}\frac{dx}{dt}\) (vi) \(\frac{d}{dx}\)f(g[x]) = f’(g(x))+g’(x) Where f’(g(x)) =\(\frac{df}{dg}\) Or \(\frac{dy}{dx}\)=\(\frac{dy}{dv}\frac{dv}{dx}\)
The derivatives of some simple functions x :
f(x)
df(x)/dx
(i) c
0
(ii) cx
c
(iii) cx2
2cx
(iv) xn
nxn-1
(v) 1/x
-1/x2
(vi) ex
ex
(vii) ecx
c ecx
(viii) ln x = logex
1/x
(ix) sin x
cos x
(x) cos x
− sin x
(xi) tan x
sec2 x
(xii) cot x
− cosec2 x
(xiii) sec x
tan x.sec x
(xiv) cosec x
− cosec x.cot x
Geometrically Interpretation of dy/dx : Consider a function y = f(x) , where x is the independent variable and y is the dependent variable. Geometrically, this relationship can be represented as a graph of function y = f(x), regarding y and x as Cartesian coordinates, Fig.(a). From Fig. (a), we see that Δy/Δx is the slope of the secant line joining an arbitrary point A ≡ (x, y) and a nearby point B ≡ (x + Δx, y + Δy), Δy and Δx being the differences in the y- and x-coordinates of A and B. As Δx —> 0, A remains fixed while B moves along the curve toward A, and the line AB rotates about A toward its limiting position — the tangent line at A. Thus, dy/dx gives the slope of the tangent at A to the curve y = f(x).

Geometrical interpretation of the integral of a function : The integral of a function y = f (x) is closely related to the area under the curve y = f(x) plotted in rectangular coordinates. Consider the Cartesian graph of a given function y = f (x), as shown in Fig. Let us calculate the area DEBAD under the curve between the limiting ordinates DA at x = a and EB at x = b. An approximation to this area can be obtained by dividing the region into a large number n of narrow rectangles of width Δx = xi—xi-1, as shown. The area ΔAi of one such rectangle, located between xi-1 and xi, is ΔAi = f(xi) Δxi = f(xi)(xi − xi-1) Then, the total area DEBAD will be approximated by the sum of all the ΔAi contributions lying between x = a and x = b, that is, Area DEBAD = \(\sum \limits_{i=1}^{n}ΔA_i\) =\(\sum \limits_{i=1}^{n}f(x_i)(x-x_{i-1})\) In the limiting case where the number of rectangles increases without bound, i.e. n → ∞ the sum approaches the actual area under the Area DEBAD = \(\lim\limits_{n\to\infty}(\sum \limits_{i=1}^{n}ΔA_i)\) =\(\lim\limits_{n\to\infty}(\sum \limits_{i=1}^{n}f(x_i)(x-x_{i-1}))\) In this limit, Δx = xi − xi-1 approaches zero and can be written as a differential quantity dx. Also, in this limit, the quantity ΔA/Δx approaches \(\frac{dA(x)}{dx}\), the derivative of the function A(x). Then, in this limit, dA(x) = f(x)dx or f(x) =\(\frac{dA(x)}{dx}\) where A(x) = area DEBAD. ∴ Area DEBAD = \(\lim\limits_{Δx\to 0}(\sum \limits_{x=a}^{x=b}ΔA(x))\) =\(\lim\limits_{Δx\to 0}(\sum \limits_{x=a}^{x=b}f(x)Δx))\) The limiting value of the sums in the above equation defines the integral of the function f (x), which is conveniently written using the integral sign ∫ to denote the use of the limiting process Δx—> 0, in which we write ΔA and Δx as differential quantities dA and dx. Area DEBAD = \(\int \limits_{a}^{b}dA(x)=\int \limits_{a}^{b}f(x)dx\) The integral so defined is referred to as a definite integral between the lower limit x = a and the upper limit x = b. Its value depends upon the specific form of the function f (x) and also upon the lower and upper limits.

Properties of integration :
(1) \(\int [f_1(x)+f_2(x)]dx=\int [f_1(x)dx +\int f_2(x)]dx\)
(2) \(\int kf(x)dx=k\int f(x)dx\) , for k is constant
Indefinite integrals of some basic functions : = \(\frac{1}{a}\)ln(sec ax} +C
f(x)
\(\int f(x)dx\)
(i) 1
\(\int dx\) = x + C
(ii) k
\(\int k\,dx\)=\(k\int dx\) = kx + C
(iii) xn
\(\int x^ndx\)=\(\frac{x^{n+1}}{n+1}\)+C (provide x ≠ -1)
(iv) 1/x
\(\int \frac{x}{dx}\)= ln + C
(v) eax
\(\int e^{ax}dx\)= \(\frac{1}{a}e^{ax}\) +C
(vi) sin ax
\(\int sin\,ax\,dx\)=\(-\frac{1}{a}\)cos ax +C
(vii) cos ax
\(\int cos\,ax\,dx\)=\(\frac{1}{a}\)sin ax +C
(viii) tan ax
\(\int tan\,ax\,dx\)=\(-\frac{1}{a}\)ln(cos ax} +C
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 1: Units and Measurements – Online Notes
Next Chapter : Chapter 3: Motion in a Plane – Online Notes
We reply to valid query.