Notes-Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Different states of matter :
- There are three states of matter namely solid, liquid and gas.
- Three states of matter are interconvertible by exchange of heat.
Distinguishing points between Solid, Liquid and Gas :
(i) Characteristics of Solid :
- Mean separation ≈ 3-5 A0
- Particles are tightly held, and have regular arrangement of atoms/molecules
- Particles cannot move freely as they occupy fixed positions.
- Solid has definite shape and volume
- Very small Intermolecular space
- Volume change is small
- Practically Non- compressible
(ii) Characteristics of Liquid :
- Mean separation ≈ 3-10 A0
- Particles are loosely packed, irregular arrangement of particles
- Particles can move a small distance within the liquid
- Liquid takes the shape of the container and has definite volume.
- Moderate Intermolecular space
- Moderate effect on volume change
- Small Compressibility
(iii) Characteristics of Gas :
- Mean separation ≈ 5 A0
- Particles are more loosely packed, highly irregular arrangement
- Particles are in continuous random motion.
- Gas takes the shape and the volume of its container.
- Large Intermolecular space.
- Volume change significantly high.
- Compressible
Intermolecular Forces :
- Intermolecular forces are the attractive forces as well as repulsive forces present between the neighbouring molecules.
- The attractive force decreases with the increase in distance between the molecules. The intermolecular forces are strong in solids, less strong in liquids and very weak in gases.
- Due to this variation in the strength of intermolecular forces, the properties of matter in three states are different.
The physical properties of a matter which depend upon intermolecular forces are:
- (i) melting point, (ii) boiling point, (iii) vapour pressure, (iv) viscosity, (v) surface tension, (vi) rate of evaporation, (vii) solubility.
Types of intermolecular forces :
There are five types of intermolecular forces as follows :
- Dipole-dipole interactions
- Ion-dipole interactions
- Dipole-induced dipole interaction
- Hydrogen bonding
- London dispersion forces
(i) Dipole-dipole interactions :
Polar molecules experience dipole-dipole forces due to electrostatic interactions between dipoles on neighboring molecules.
Polar molecules or Polar covalent molecules :
Polar covalent molecule is also described as “dipole” meaning that the molecule has two ‘poles’.
Example :
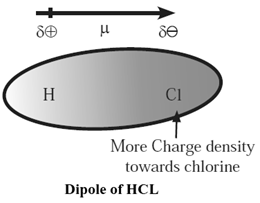
In a molecule like HCl, due to the difference in the electronegativities of H and Cl, the bonding electron pair between H and Cl is shifted towards more electronegative Cl atom. This gives partial positive charge, (+ δ) to H atom and equal negative charge, (— δ) on Cl atom, forming a polar molecule.
Such a polar molecule is called an electric dipole or dipole and it behaves like a tiny molecular magnet.
Dipole moment : Dipole moment of al polar molecule is the product of the magnitude of the charge (Q) and the distance (r) between the centres of positive and negative charges. It is represented as, μ = Q × r
- Dipole moment is a vector quantity and represented by a small arrow with tail at the positive centre and head towards the negative centre.
- The polar molecules have permanent dipole moment.
Dipole-dipole interaction :
Dipole-dipole interaction results in generating a force of attraction between neighbouring polar molecules due to attraction between the two oppositely charged ends of the polar molecules. This interaction arises due to electrostatic force of attraction.
Example : In a polar molecule HCL, H carries partial positive charge (+ δ) and Cl carries partial negative charge (—δ), due to the difference in their electronegativity.
All HCl molecules align themselves in such a way that their oppositely charged ends face each other.
- The strength of dipole—dipole interaction depends upon the magnitude of dipole moment (μ) of the polar molecule.
- Higher the dipole moment, stronger is the intermolecular forces, generally leading to higher boiling points. (See Table)
- Other examples are HBr, H2S, NH3, etc.
Effect of dipole moments on boiling point :
| Substance | Molar Mass (amu) | Dipole Moment (D) | b.p. (K) |
| CH3 - CH2 - CH3 | 44.10 | 0.1 | 231 |
| CH3 - O - CH3 | 46.07 | 1.3 | 248 |
| CH3 - Cl | 50.49 | 1.9 | 249 |
| CH3 - CN | 41.05 | 3.9 | 355 |
(ii) Ion-dipole interactions :
- An ion-dipole force is the result of electrostatic interactions between an ion (cation or anion) and the partial charges on a polar molecule.
- The strength of this interaction depends on the charge and size of an ion. It also depends on the magnitude of dipole moment and size of the molecule.
- Smaller the size of an ion, more is the charge density and hence stronger is the interaction.
- Since cations have smaller size than anions, the interaction between a cation and a negative end of a polar molecule is stronger than the interaction between anion and the positive end of the ‘polar molecule.
Example :
Consider an aqueous solution of NaCl, which contains cation Na+ and anion Cl— interacting with the polar water molecule.
Ions Na+ and Cl— undergo hydration by interaction with H2O polar molecules, with
oppositely charged poles of H2O.
Each Na+ and Cl— are surrounded by six water molecule.
Hydration of ions : When an ionic compound, like an electrolyte is dissolved in water, the ions get separated and surrounded by water molecules which is called Hydration of ions.
- Cations are smaller in size while anions are larger in size than their respective neutral atoms.
- Therefore, cations are hydrated more strongly than anions.
- Ion-dipole forces increase in the order of Na+ < Mg3+ < Al2+
(iii) Dipole-Induced dipole interaction :
When polar molecules (like H2O, NH3) and nonpolar molecules (like benzene-C6H6) approach each other, the polar molecules induce dipole in the non-polar molecules.
Hence ‘Temporary dipoles’ are formed by shifting of electron clouds in nonpolar molecules.
Example :
- Ammonia (NH3) is polar and has permanent dipole moment while Benzene (C6H6) is non polar and has zero dipole moment.
- The force of attraction developed between the polar and nonpolar molecules is of the type dipole - induced dipole interaction.
- Dipole-induced dipole interaction has a less strength than dipole-dipole interaction.
(iv) London Dispersion Force :
The intermolecular forces between non-polar molecules are called London-dispersion forces or dispersion forces.
- These forces are also called van der Waals forces.
- These forces depend upon the polarisability of the atom or a molecule. It is the weakest intermolecular force.
- In general all atoms and molecules experience these forces due to the motion of electrons.
- The electron distribution in an atom is asymmetrical resulting in a short lived dipole moment.
- This momentary dipole on one atom induces momentary dipoles on neighbouring atoms resulting in weak attractive forces.
- The strength of London—dispersion forces increases with an increase in atomic or molecular size, molecular mass and number of electrons present in one atom or a molecule.
- London—dispersion forces are stronger in a long chain of atoms in the molecule.
- Substances composed of molecules such as O2, CO2, N2, halogens, methane gas, helium and other noble gases show van der Waals force of attraction.
Polarisability :
- The distortion in the electron cloud caused by the attractive and repulsive interactions between the nuclei of two approaching non-polar molecules is known as polarisability.
- The more electrons in a molecule, the more polarisable it is.
- Polarisability describes how much an external electric field may alter an atom's or molecule's electron cloud.
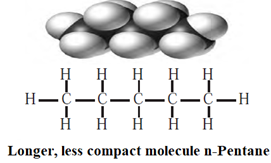
Q. Why n-Pentane has higher boiling point than neopentane.
London dispersion forces are stronger in a long chain of atoms where molecules are not compact. This can affect physical property such as B.P.
(i) n—Pentane, has a long chain of carbon atoms, hence they have strong London—dispersion forces of attraction. Therefore n-pentane requires higher energy to separate the molecules and has a higher boiling point (309.4 K).
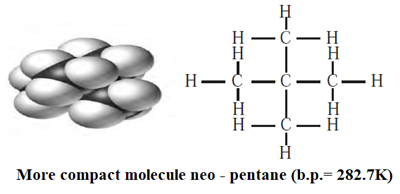
(ii) Neo-pentane, has a short chain of carbon atoms, hence involve weak London—dispersion forces. Therefore, it requires comparatively less energy to separate the molecules and has less boiling point (282.7 K) than n-pentane.
Boiling points of inert gasses :
- The atoms of inert gases are non-polar, hence, the interatomic interaction arises due to London forces or dispersion forces.
- As atomic mass of the inert gas increases, atomic number and atomic size increase. Hence, interatomic attraction increases. Therefore, the boiling point of inert gases increases with the increase in atomic mass.
(v) Hydrogen Bonding :
Hydrogen bond:The electrostatic force of attraction between positively charged hydrogen atom of one molecule and negatively charged atom of the other molecule developing a strong dipole-dipole interaction is called hydrogen bond.
- This can be considered as a special case of dipole—dipole interaction.
- When hydrogen atom is bonded to a strong electronegative atom like N, O, F or Cl, then due to a large difference in their electronegativities, there arises separation of the charges of large magnitude between H atom and other electronegative atom.
- In this case H atom carries a partial positive charge and other bonded atom carries a partial negative charge.
Example : N—δ —H+ δ, O—δ —H+ δ, F—δ —H+ δ, H+ δ —Cl—δ
The oppositely charged ends of these polar molecules are strongly attracted by electrostatic force giving rise to the hydrogen bonding.
Intermolecular and Intramolecular Hydrogen bond
(i) A hydrogen bond present between two like or unlike molecules, represents Intermolecular Hydrogen bond.
(ii) Hydrogen bond which occurs within the same molecule represents Intramolecular Hydrogen bond.
Effect of hydrogen bonding :
- Due to strong intermolecular hydrogen bonding, the liquids have considerably higher boiling points. For example, water has high boiling point, 100 °C, due to hydrogen bonding.
- Due to hydrogen bonding viscosity of a liquid increases.
- Hydrogen bond plays a vital role in determining the structure and properties of proteins and nucleic acids present in all living organisms.
Intermolecular Forces and Thermal energy :
- Thermal energy is the origin of kinetic energy of the particles of matter that arises due to movement of particles.
- Thermal energy is directly proportional to the temperature.
- Gaseous state of matter has very weak inter-molecular forces and high thermal energy.
- Liquids have less thermal energy and stronger intermolecular forces while solids have very low thermal energy but very strong intermolecular forces.
- By changing thermal energy, the physical state of a matter may be changed.
Comparison of Intermolecular Forces :
| Force | Strength | Characteristics |
| Ion-dipole | Moderate (10 - 50 kJ/mol) | Occurs between ions and polar solvents |
| Dipole-dipole | Weak (3 - 4 kJ/mol) | Occurs between polar molecules |
| London dispersion | Weak (1 -10 kJ/mol) | Occurs between all molecules; strength depends on size, polarizability |
| Hydrogen bond | Moderate (10 - 40 kJ/mol) | Occurs between molecules with O-H, N-H, and H-F bonds |
Know This :
|
Characteristic properties of Gases :
The gaseous state is characterized by the following physical properties :
- Gases are lighter than solids and liquids i.e. possess lower density.
- Gases do not possess a fixed volume and shape. They occupy entire space available and take the shape of the container.
- Gas molecules are widely separated and are in continuous, random motion. Therefore, gases exert pressure equally in all directions due to collision of gas molecules, on the walls of the container.
- In case of gases, intermolecular forces are weakest.
- Gases possess the property of diffusion which is a spontaneous homogenous inter mixing of two or more gases.
- Gases are highly compressible.
Measurable properties of Gases :
Some Important measurable properties of the gases are given below :
(i) Mass : The quantity of a gas is expressed in mass m and measured in SI units kilogram (kg). It is also expressed in number of moles, n.
n = \(\frac{\text{mass in grams}}{\text{molar mass in grams per mole}}=\frac{m}{M}\)mol
1 mol of a gas contains 6.022 x 1023 molecules
n = \(\frac{\text{Number of molecules}}{\text{Avogadro constant}}\)
= \(\frac{N}{N_A}=\frac{N}{6.022×10^{23}}\)
One mole of a gas at STP (273 K and 1 atm) occupies 22.4 dm3.
(ii) Volume :It is expressed in Litres (L), mililitres (mL), cubic centimeter (cm3), decimeter cube (dm3) and meter cube (m3)
1 L = 1000mL = 1000 Cm3 = 1 dm3
1 m3 = 103 dm3 = 103 L = 106 cm3 = 106 mL.
(iii) Pressure : It is defined as force (f) per unit area (a).
∴ Pressure = f/a
SI unit of pressure is pascal (Pa) or Newton per meter square (Nm2)
1 Pa =1 Nm2=1 kg.m—1s2
1 bar = 1 x 103 Pa
1 atm=76 cm of Hg=76O mm of Hg = 760 torr
1 atm = 101.325 kPa = 101325 Pa = 1.1325 bar
(iv) Temperature : The temperature is measured in degree celsius (°C), degree Fahrenheit (°F) and Kelvin (K).
The relationship between temperature units is,
\(\frac{°C}{5}=\frac{°F-32}{9}\)
∴ °C = \(\frac{5}{9}\)(°F — 32) and °F = \(\frac{9}{5}\) °C + 32.
Kelvin temperature, also called as absolute temperature, is given by
TK = t °C + 273.15 or approximately,
TK = t°C + 273.
(v) Density : It is the mass per unit volume.
d = m/V
SI Unit of density is kg m—3.
In the case of gases, relative density is measured with respect to hydrogen gas and is called vapour density.
∴ Vapour density = (\frac{molar\,\,mass}{2}\)
(vi) Diffusion : The process of mixing of two or more gases is called diffusion. It is measured as,
Rate of diffusion = \(\frac{\text{Volume of gas diffused}}{\text{Time required for diffusion}}\)
SI unit of rate of diffusion is, m3s—1, dm3s—1 or cm3s—1.
Gas Laws :
- Pressure, volume, temperature and the number of moles these four variables and measurable properties of the gases are related with one another through different gas
- Relationships between P, V, n and T are summarized by five gas laws: Boyle’s law, Charles’ law, Gay Lussac law, Avogadro law and Dalton’s
Boyle’s law (Pressure-Volume Relationship) :
For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of a gas is inversely proportional to the volume (V) of gas.
OR
At constant temperature, the pressure of fixed amount (number of moles) of a gas varies inversely with its volume.
Explanations : Mathematically Boyle's law can be stated as,
P ∝ \(\frac{1}{V}\) at constant mass or moles and temperature of a gas
∴ P = \(\frac{K_1}{V}\) where K1 is a proportionality constant.
P x V = K1 = constant
If a given mass of a gas at constant temperature is at the initial state of pressure (P1) and volume (V1) and changes to the final state of pressure P2 and volume V2 then,
P1 × V1 = K1 and P2 × V2 = K1
∴ P1V1 = P2V2.
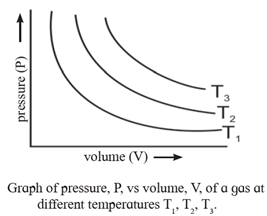
Graphical Representation :
Variation of pressure of a gas with volume at constant temperature :
Graph of pressure (P) versus volume (V) at given temperature :
By Boyle's law, at constant temperature for a given mass of a gas,
P × V = constant
where P is pressure and V is volume of the gas.
When the volume of the given mass of a gas is plotted against pressure at constant temperature a parabolic curve is obtained. The volume of a gas decreases exponentially.
Graphical representation of variation of product of pressure (P) and volume (V) of a gas against pressure at constant temperature :
By Boyle's law at constant temperature for the given mass of a gas, product of pressure and volume, (PV) is always constant.
P × V = constant
Hence when product PV is plotted against pressure (P) at different constant temperatures, a line parallel to P axis is obtained. This verifies Boyle's law over a range of temperature.
Variation of pressure of a gas with reciprocal of its volume at different constant temperatures :
By Boyle's law, at constant temperature, the pressure of a given mass of a gas is inversely proportional to its volume.
P ∝ \(\frac{1}{V}\) at constant temperature.
P = K1 × \(\frac{1}{V}\) where K1 is a proportionality constant.
With the increase in pressure (P), the volume (V) of the gas decreases hence reciprocal increases.
Hence the graph of P against will be a straight line passing through the origin, with a positive slope.
Three graphs A, B and C respectively at three different constant temperatures, T1, T2 and T3 are shown in Fig. (T1 < T2 < T3 ).
Boyle's law in terms of density of the gas :
Density of a gas is the ratio of mass (m) of a gas to its volume (V). It is represented as,
Density = \(\frac{\text{mass of gas}}{\text{volume of gas}}\)
∴ d = m/V
The density of a gas depends on temperature and pressure. Hence at constant temperature, density (d) of the gas depends on its pressure (P).
∴ V = m/d
By Boyle's law, at constant temperature,
P × V = K1 (constant)
P × \(\frac{m}{d}\) = K1
∴ \(\frac{P}{d}\) = \(\frac{K_1}{m}\)
Since the mass (m) of the gas is constant, the ratio \(\frac{P}{d}\) must be constant at constant temperature.
∴ \(\frac{P}{d}\) = constant
P ∝ d
Hence by Boyle's law, at constant temperature and pressure for the given mass of a gas its density is directly proportional to pressure.
If d1 and d2 are the densities of a given mass of a gas at pressures P1 and P2 respectively at constant temperature, then
\(\frac{P_1}{d_1}\) = \(\frac{P_2}{d_2}\)
Charles’ Law (Temperature -Volume Relationship):
It states that at constant pressure the volume of a given mass of a gas increases or decreases by \(\frac{1}{273.15}\) of its volume at 0 °C for every degree rise or fall of temperature.
OR
It states that at constant pressure, the volume of the given mass of a gas is directly proportional to its absolute temperature.
Charles’ law explains that at constant pressure, gases expand on heating and contract on cooling. Thus hot air is less dense than cold air.
Explanation :
Let V0 be the volume of a given mass of a gas at 0°C. If the temperature is increased to t °C, at constant pressure, then By Charles’s law, the increase in the volume will be,
ΔV = V0 × \(\frac{t}{273.15}\)
∴ Final volume Vt will be,
Vt = V0 + ΔV
Vt = V0 + V0 × \(\frac{t}{273.15}\) = V0 \((1+\frac{t}{273.15})\)
= V0 \((\frac{273.15+t}{273.15})\)
Now on Kelvin temperature scale,
t °C + 273.15 = T K, where T is absolute temperature.
At 0 °C,
T0 = 273.15 + 0 = 273.15 K
∴ Vt = V0 × \(\frac{T}{T_0}\)
∴ \(\frac{V_t}{T}=\frac{V_0}{T_0}\) = constant = K2
∴ \(\frac{V}{T}\) = K2 or V = K2T
V ∝ T
Hence, in general, if V1 and V2 are the volumes of a given mass of a gas at constant pressure and absolute temperatures T1 and T2 respectively, then Charles’ law can be represented as \(\frac{V_1}{T_1}=\frac{V_2}{T_2}\)
Verification of Charles’ law by plotting graphs of volume against temperature at different constant pressures :
Explanation :
By Charles’ law, the volume (V) of the given mass of a gas at constant pressure is directly proportional to the absolute temperature (T).
V ∝ T or V = K2T
- Hence, when volume (V) is plotted against absolute temperature (T) at constant pressure, a straight line with a positive slope and passing through the origin (0 K) is obtained.
- Charles’ law can be verified by plotting the graphs of V against T at different constant pressures, for example 1 bar, 2 bar and 5 bar.
- These graphs are called isobars, as shown in the below Fig.
Isobars : A graph of volume (V) vs absolute temperature (T) at a constant pressure is known as isobar.
Absolute zero temperature and Charles law :
If V0 is the volume of a given mass of a gas at 0 °C, then the volume V, at a temperature t °C is given by Charles law as,
Vt = V0 + V0 × \(\frac{t}{273.15}\) = V0 \((1+\frac{t}{273.15})\)
It is evident from the graph, that as the temperature decreases volume of the gas
decreases, and the graph intersects temperature axis (or x-axis), at — 273.15 °C, i.e., 0 K at which the volume of the given mass of a gas becomes absolutely zero.
V— 273.15 °C = V0 \((1+\frac{-273.15}{273.15})\) = 0
In fact all the gases get liquefied or solidified before the temperature, — 273.15 °C is reached.
This lowest hypothetical temperature (—273.l5 °C) is called Absolute zero denoted
by 0K.
Hence, on Kelvin temperature scale, —273.15 °C is considered the origin (or zero) of Kelvin temperature.
Various real life examples of Charles law :
- As the temperature rises in the summer, the volume of air in the tyre expands, resulting in tyre bursts.
- When water is boiled, the vapour pushes the lid of the vessel.
- When an air filled balloon is kept in a fridge, it shinks at low temperature and on removal of it outside, it expands.
- When milk is boiled, a creamy layer on the top rises due to increase in volume of air between milk and creamy laver.
- The volume of hot air balloons is large and the density is low. Hence the hot air balloons fly high.
Gay-Lussac’s Law: (Pressure-Temperature Relationship) :
Gay-Lussac’s Law states that at constant volume, the pressure of a given mass of a gas varies directly with the (absolute) temperature.
Explanation: If P is the pressure of a given mass of a gas at absolute temperature T, then at constant volume, by Gay Lussac’s Law,
P ∝ T ∴ P = K3 x T where K3 is a proportionality constant.
P/T = K3 = constant.
Hence, in general, at different conditions of pressure (P1, P2 and P3) and absolute temperature (T1, T2 and T3) at constant volume, we can write,
\(\frac{P_1}{T_1}=\frac{P_2}{T_2}=\frac{P_3}{T_3}\) = constant.
Graphical Representation :
We know, Gay-Lussac’s Law states that at constant volume, the pressure of a given mass of a gas varies directly with the (absolute) temperature.
P ∝ T ∴ P = K3 x T where K3 is a proportionality constant.
When a graph is plotted between pressure (P) in atm and Temperature (T) in kelvin, a straight line is obtained as shown in below Fig. It is known as isochore.
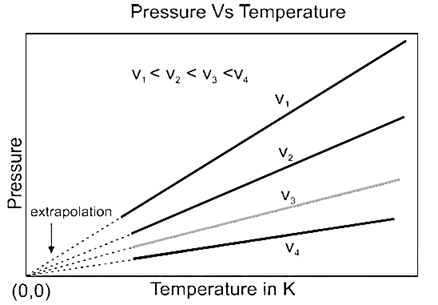
- With the help of this law, one can understand relation between pressure and temperature in day to day life.
Example of Gay-Lussac’s Law:
- While running a car during hot summer or winter, due to friction of automobile tyres on road, temperature of air in the tyres increases. Since the volume of tyres is constant, the pressure in the tyres increases.
- In winter due to low temperature volume of air decreases. Since the volume of tyres is constant, the pressure in the tyres
- Therefore, we observe the pressure in the automobile tyres changes during hot summer or winter season.
Avogadro Law: (Volume-Amount Relationship) :
Avogadro’s law can be stated in different ways as follows :
- At constant pressure and temperature, equal volumes of all gases contain equal number of molecules.
- Equal volumes of all gases under identical conditions of pressure and temperature contain equal number of molecules.
- At constant pressure and temperature, the volume of a gas is directly proportional to the number of moles of the gas.
Explanation :
According to Avogadro’s law, at constant pressure and temperature, the volume of the gas is directly proportional to the number of molecules present in it. Hence,
V ∝ number of molecules (at constant P and t)
∝ \(\frac{\text{number of molecules}}{N_A}\) × NA
∝ number of moles × NA
Since Avogadro’s number NA is constant,
∴ V ∝ number of moles (n)
∴ V ∝ n
or V = K4 x n, where K4 is a proportionality constant.
∴ V/n = K4 = constant
Hence, Avogadro's law can be expressed mathematically as follows :
Volume of a gas at constant pressure and temperature is proportional to number of moles of a gas.
Molar volume : As the volume of a gas is directly proportional to number of moles, one mole of any gas at STP occupies 22.414 Lmol-1 volume. This volume is known as molar volume.
- 1 mole of a gas contains Avogadro number of molecules = 6.022 × 1023.
Avogadro Law can be well represented from below Fig.
Know This :
|
Relation between molar mass and density (d) of a gas :
By Avogadro’s law,
Volume of a gas ∝ number of moles of gas
∴ V ∝ n
n = \(\frac{\text{mass of a gas}}{\text{molar mass of a gas}}=\frac{m}{M}\)
∴ V ∝ \(\frac{m}{M}\) or V = \(K_4×\frac{m}{M}\)
∴ M = (K_4×\frac{m}{V}\)
Since density of a gas, d = \(\frac{m}{V}\)
∴ M = K4 × d OR d ∝ M
Hence, density of a gas at given pressure and temperature is directly proportional to its molar mass.