Chemical Kinetics
Maharashtra Board-Class-12-Chemistry-Chapter-6
Notes-Part-2
Topics to be Learn : Part-2
|
Integrated rate law :
It describes how rate of a reaction depends on the concentration of reactants in terms of derivatives.
Integrated rate laws : The equations which are obtained by integrating the differential rate laws (expressions) and which provide direct relationship between the concentrations of the reactants and time are called integrated rate laws.
For example, integrated rate law for first order reaction is represented as,
k = \(\frac{2.303}{t}log_10\frac{[Reactant]_{final}}{[Reactant]_{initial}}\)
Expression for integrated rate law (equation) for the first order reaction :
Consider the following first order reaction, A → B
The rate of the chemical reaction is given by the rate law expression as,
Rate, R = k [A]
where [A] is the concentration of the reactant A and k is the velocity constant or specific rate of the reaction.
The instantaneous rate is given by,
R = k [A] = \(\frac{-d[A]}{dt}\)
∴ \(\frac{-d[A]}{[A]}\) = k.dt
If [A]0 is the initial concentration of the reactant and [A]t at time t, then by integrating the above equation,
\(\int_{[A]_0}^{[A]_t}\frac{d[A]}{[A]}\) =\(k\int_{0}^{t}dt\)
∴ \(-log_e\frac{[A]_t}{[A]_0}\) = kt …(1)
∴ \(log_e\frac{[A]_0}{[A]_t}\) = kt
∴ k = \(\frac{1}{t}log_e\frac{[A]_0}{[A]_t}\)
∴ k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\) ….(2)
This is the integrated rate equation for the first order reaction. This is also called integrated rate law.
The rate law can be written in the following forms
(i) Exponential rate law expression for the first order reaction :
From Eq. (1)
\(-log_e\frac{[A]_t}{[A]_0}\) = kt
By taking antilog of both sides we get
\(\frac{[A]_t}{[A]_0}\) = e−kt
∴ [A]t = [A]0e−kt …(3)
where [A]0 and [A]t are the concentrations of the reactant when t = 0 and t = t respectively.
- Thus, the concentration of the reactant decreases exponentially with time and the time required to complete the first order reaction will be infinity.
- Another feature of the exponential behaviour is the time required to complete a definite fraction of the reaction is always constant. Therefore, the first order reactions are also described in terms of the half-life of the reaction (t1/2)
(ii) Considering the concentration of the product :
Let ‘a’ mol dm-3 be the initial concentration of A at t = 0
Let x mol dm-3 be the concentration of A that decreases (reacts) during time t. The concentration of A that remains unreacted at time t would be (a − x) mol/dm3
Substitution of [A]0 = a and [A]t = (a - x) in eq. (2)
∴ k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\) …(4)
Equations (2), (3) and (4) represent the integrated rate law of first order reactions.
Units of rate constant for the first order reaction:
The integrated rate law is
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
Because \(log_{10}\frac{[A]_0}{[A]_t}\) is unitless quantity, the dimensions of k will be (time)−1. The units of k will be s−1, min−1or (hour) −1
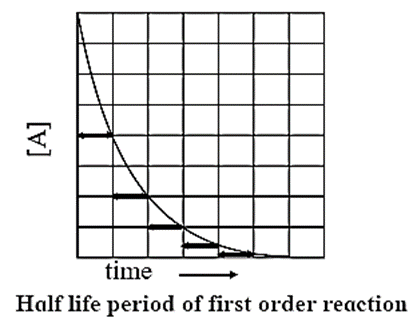
Half-life of a reaction : The time required to reduce the concentration of the reactant to half of its initial value is called the half-life period or the half-life of the reaction.
If t1/2 is the half-life of a reaction, then at t = t1/2,
X = a/2, hence a — x = a — a/2 = a/2
Now,
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\)
∴ t = \(\frac{2.303}{k}log_{10}\frac{a}{(a-x)}\)
Hence,
t1/2 = \(\frac{2.303}{k}log_{10}\frac{a}{(a-a/2)}\) = \(\frac{2.303}{k}log_{10}\frac{a}{(a/2)}\)
= \(\frac{2.303}{k}log_{10}2\) = \(\frac{2.303×0.3010}{k}\)
∴ t1/2 = 0.693/k
Hence, for a first order reaction, the half-life of the reaction is independent of the initial concentration of the reactant.
Graphical representation of the first order reactions :
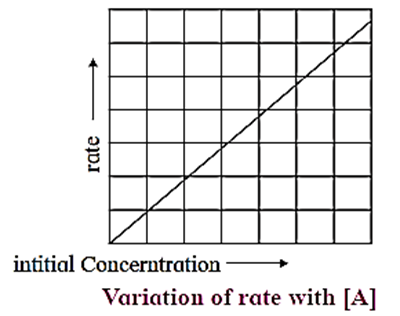
(i) A graph of rate of a reaction and concentration :
The differential rate law for first order reaction, A → Products is represented as,
Rate = \(\frac{-d[A]}{dt}\) = k[A]
Rate = k x [A], (y = mx). When the rate of a first order reaction is plotted against concentration, [A]t, a straight line graph is obtained.
With the increase in the concentration [A]t, rate R, increases. The slope of the line gives the value of rate constant k.
(ii) A graph of concentration against time : When the concentration of the reactant is plotted against time t, a curve is obtained. The concentration [A]t, of the reactant decreases exponentially with time. The variation in the concentration can be represented as,
[A]t = [A]0e−kt

where [A]0 and [A]t are initial and final concentrations the reactant and k is the rate constant. The time required to complete the first order reaction is infinity.
(iii) A graph of log10(a — x) against time t :
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\)
∴ k = \(\frac{2.303}{t}[log_{10}a-log_{10}(a-x)]\)
∴ \(\frac{kt}{2.303}\) = \(log_{10}a-log_{10}(a-x)\)
∴ log10(a − x) = \(-\frac{kt}{2.303}\) + log10 a ……(y = −mx + c)
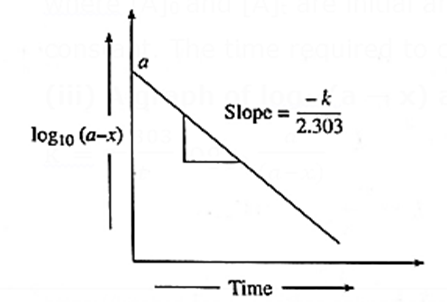
When log10(a — x) is plotted against time t, a straight line with negative slope is obtained, from which the velocity constant k can be calculated.
A graph of half-life period and concentration :
The half-life period, t1/2 of a first order reaction is given by t1/2 = 0.693/k, Where k is the rate constant.
For the given reaction at constant temperature, t1/2 is constant and independent of the concentration of the reactant.
Hence when a graph of t1/2 is plotted against concentration, a straight line parallel to the concentration axis (slope = zero) is obtained.

A graph of \(log_{10}\frac{a}{(a-x)}\) against time :
The rate constant, for a first order reaction is represented as,
k = \(\frac{2.303}{t}log_{10}\frac{a}{(a-x)}\) = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
where [A]0 and [A]t, are the respective initial and final concentrations of the reactant after time t.
∴ \(log_{10}\frac{a}{(a-x)}\) = \(\frac{k}{2.303}×t\) ….(y = mx)
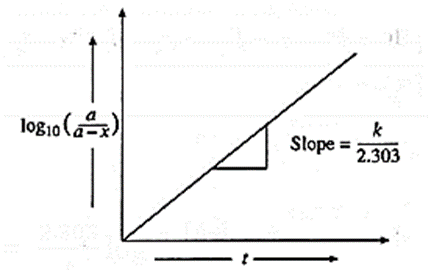
When \(log_{10}(\frac{a}{a-x})\) is plotted against time t, a straight line graph passing through the origin is obtained and the slope gives the value of k/2.303.
From this slope, the rate constant can be calculated.
Examples of first order reactions
Some examples of reactions of first order are :
(i) Decomposition of H2O2 :
2H2O2(l) → 2H2O(l) + O2(g),
Rate = k[H2O2]
(ii) Decomposition of N2O5 :
2N2O5(g) → 4NO2(g) + O2(g),
Rate = k [N2O5]
Integrated rate law for gas phase f reactions :
For the gas phase reaction,
A(g) → B(g) + C(g)
Let initial pressure of A be Pi that decreases by x within time t.
Pressure of reactant A at time t
PA = Pi – x ….(1)
The pressures of the products B and C at time t are
PB = PC = x
The total pressure at time t is then
P = Pi – x + x + x = Pi + x
Hence, x = P – Pi …….(2)
Pressure of A at time t is obtained by substitution of Eq. (2) into Eq. (1). Thus
PA = Pi – (P – Pi) = Pi – P + Pi = 2Pi – P
The integrated rate law turns out to be
k = \(\frac{2.303}{t}log_{10}\frac{[A]_0}{[A]_t}\)
The concentration now expressed in terms of pressures.
Thus, [A]0 = Pi and [A]t = PA = 2Pi – P
Substitution gives in above
∴ k = \(\frac{2.303}{t}log_{10}\frac{P_i}{2P_i-P}\)
P is the total pressure of the reaction mixture at time t
Zero order reaction : A reaction in which the rate of the reaction does not depend on the concentration of any reactant taking part in the reaction is called zero order reaction.
Explanation : Consider photochemical reaction between H2 and Cl2 gases.
Diffused
H2(g) + Cl2(g) \(\underrightarrow{Diffused\,\,sunlight}\) 2HCl(g)
In this the rate of the reaction remains constant throughout the progress of the reaction, even if the concentrations of the reactants decrease with time, until the reactant has reacted entirely.
Hence, by the rate law,
R = k [H2]0 [Cl2]0 = k (constant).
Expression for Integrated rate law for zero order reactions :
Consider a zero order reaction, A → Products
The rate of the reaction is,
Rate = \(\frac{-d[A]}{dt}\)
By rate law,
Rate = k x [A]0 = k
∴ −d[A] = k x dt
If [A]0 is the initial concentration of the reactant A at t = 0 and [A]t is the concentration of A present after time t, then by integrating above equation,
\(\int_{[A]_0}^{[A]_t} -d[A] = \int_{t=0}^{t=t}k \,dt\)
\(-\int_{[A]_0}^{[A]_t} d[A] = k\int_{t=0}^{t=t}dt\)
\([A]_{[A]_0}^{[A]_t} = k[t]_o^t\)
− ( [A]t − [A]0 ) = kt
∴ [A]0 − [A]t = kt
∴ k = \(\frac{[A]_0-[A]_t}{t}\)
This is the integrated rate law expression for rate constant for zero order reaction.
∴ k x t= [A]0 − [A]t
[A]t = −kt + [A]0
Units of rate constant of zero order reactions :
k = \(\frac{[A]_0-[A]_t}{t}=\frac{mol\,L^{-1}}{s}\) = mol dm−3 s−1
The units of rate constant of zero order reaction are the same as the rate.
Expression for half-life period of zero order reaction.
The rate law expression for zero order reaction is,
[A]t = — kt + [A]0
where [A]0 and [A]t are the concentrations of the reactant at time, t = 0 and after time t respectively,
Half-life period, t1/2 is the time when the concentration reduces from [A]0 to [A]0/2. i.e., at
t = t1/2
[A]t = [A]0/2.
∴ \(\frac{[A]_0}{2}\) = −kt1/2 + [A]0
∴ kt1/2 = [A]0 − \(\frac{[A]_0}{2}\) = \(\frac{[A]_0}{2}\)
∴ t1/2 = \(\frac{[A]_0}{2k}\)
Hence for a zero order reaction, half-life period is directly proportional to the initial concentration of the reactant.
Graphical representation of zero oder reactions :
A graph of concentration against time : In case of a zero order reaction, the rate of reaction is independent of the concentration of the reactant.
The concentration [A]t of the reactant at a time t is given by
[A]t = −kt + [A]0 …(y = −m + c)
where [A]0 is the initial concentration of the reactant and k is a rate constant.

Hence in case of zero order reaction, when the concentration of the reactant is plotted against time, a straight line with the slope equal to −k is obtained. The concentration of the reactants decrease with time. The intercept on the concentration axis gives the initial concentration, [A]0.
A graph of rate of a reaction against the concentration of the reactant :
Rate of a Zero Order reaction is independent of the concentration of the reactant.
Rate, R = k [A]0 = k
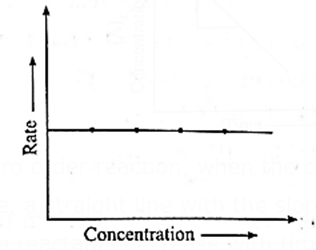
Hence even if the concentration of the reactant decreases, the rate of the reaction remains constant.
Therefore if the rate of a zero order reaction is plotted against concentration, then a straight line with zero slope is obtained indicating, no change in the rate of the reaction with a change in the concentration of the reactants.
A graph of half-life period against concentration :
The half-life period of a zero order reaction is given by, t1/2 = (\frac{[A]_0{2k}\) where [A]0 is initial concentration of the reactant and k is the rate constant. Hence the half-life period is directly proportional to the concentration.
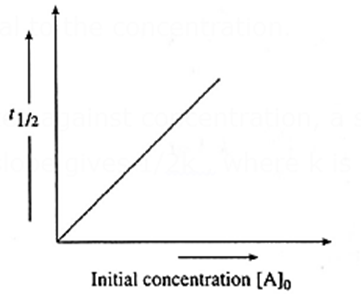
When a graph of t1/2 is plotted against concentration, a straight line passing through origin is obtained, and the slope gives 1/2k , where k is the rate constant.
Examples of zero order reactions :
Zero order reactions are not common. They take place under special conditions. They are heterogeneous catalysed reactions generally involving metals as catalysts.
Here follow some examples
(i) Decomposition of NH3 on platinum metal.
2NH3(g) → N2(g) + 3H2(g)
- Since it is a heterogeneous catalysed reaction, NH3 gaseous molecules at high pressure are adsorbed on the metal surface covering the surface area.
- The number of NH3 molecules adsorbed is small compared to NH3 molecules in the gaseous phase.
- Only the molecules adsorbed on the surface get decomposed. Hence rate of the decomposition becomes independent of the concentration (pressure) of NH3.
- Therefore the Decomposition of NH3 on platinum metal is zero order.
(ii) Decomposition of nitrous oxide in the presence of Pt catalyst.
2N2O(g) \(\underrightarrow{Pt}\) 2N2(g) + O2(g)
- Since it is heterogeneous catalysed reaction, N2O gaseous molecules are adsorbed on the metal surface covering the surface area.
- The number of N2O molecules adsorbed is small compared to N2O molecules in the gaseous phase.
- Only the molecules adsorbed on the metal surface get decomposed. Hence rate of decomposition becomes independent of the concentration (pressure) of N2O. Therefore the decomposition of N2O is a zero order reaction.
(iii) The catalytic decomposition of PH3 on hot tungsten at high pressure.
Pseudo first order reaction :
A reaction which has higher order true rate law but experimentally found to behave as first order is called pseudo first order reaction.
Explanation : Consider an acid hydrolysis reaction of an ester like methyl acetate.
CH3COOCH3(aq) + H2O(l) \(\underrightarrow{H^+_{(aq)}}\) CH3C00H(aq) + CH3OH(aq)
Since the reaction involves two substances, ester and water, it is a bimolecular reaction and the true rate law should be,
Rate = k’ [CH3COOCH3] x [H2O]
Hence the reaction is expected to follow second order kinetics. However experimentally it is found that the reaction follows first order kinetics.
This is because solvent water being in a large excess, its concentration remains constant. Hence, [H2O] = constant = k”
Rate = k’ [CH3COOCH3] x [H2O]
= k’ [CH3COOCH3] x k”
= k’ x k” x [CH3COOCH3]
If k’ x k” = k, then Rate = k [CH3COOCH3].
This indicates that second order true rate law is forced into first order rate law. Therefore this bimolecular reaction which appears of second order is called pseudo first order reaction.
Q. The reaction
C12H22O11(aq) + H2O(l) → C6H12O6(aq) + C6H12O6(aq)
(sucrose) (excess) (glucose) (fructose)
Can it be of pseudo-first order type ?
The inversion of cane sugar (sucrose) is an acid catalysed hydrolysis reaction which can be represented as,
C12H22O11(aq) + H2O(l) → C6H12O6(aq) + C6H12O6(aq)
(sucrose) (excess) (glucose) (fructose)
This is a bimolecular reaction. Hence, the true rate law for the reaction should be,
Rate = k [C12H22O11] [H2O]. This shows that the reaction should be second order.
Since water (H2O) is in large excess, its concentration remains constant and the rate depends only upon the concentration of cane sugar.
∴ Rate = k [C12H22O11]
Therefore the second order true rate law becomes first order rate law. Hence the inversion of cane sugar is a pseudo first order reaction.
Collision theory of bimolecular reactions :
Collision between reactant molecules :
- In order for a reaction to happen, the reacting species (atoms, ions, or molecules) must come into contact with one another and collide. As a result, the rate of the reaction will depend on the frequency and rate of collisions, which rise with temperature and the number of reacting species.
- As opposed to the rate of collisions between reacting species in gaseous or liquid phases, it is seen that the rate of reaction is extremely low. This implies that not every collision will result in a reaction. As a result, in addition to collision frequency, another factor like the energy of the interacting species must be taken into account.
Activation :
For the reaction to occur the colliding reactant molecules must possess the minimum kinetic energy. This minimum kinetic energy is the activation energy. The reaction would occur only if colliding molecules possess kinetic energies equal to or greater than the activation energy.
Orientation of reactant molecules : The concept of activation energy is satisfactory in case of simple molecules or ions but not in case of complex or higher polyatomic molecules. It is observed that the rates of reaction are less as compared to the rates of collisions between activated molecules with activation energy.
This suggests that in addition, the colliding molecules must have proper orientations relative to each other during collisions.
For example, consider the reaction,
A — B + C → A + B — C.
For the reaction to occur, C must collide with B while collisions with A will not be fruitful. Since B has to bond with C.
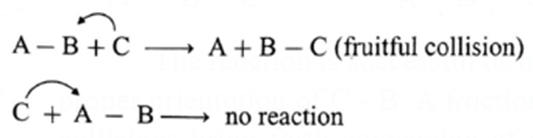
Potential energy barrier :
Consider again the reaction
A + C - B → A - B + C
During a course of collision, new bond A - B developes. At the same time bond C – B breaks. A configuration in which all the three atoms are weakly connected together is called activated complex.
A + B - C → A----B----C → A - B + C
To attain the configuration A----B----C atoms need to gain energy, which comes from the kinetic energy of colliding molecules.
The energy barrier between reactants and products is shown in below Fig.
The reactant molecules need to climb up and overcome this before they get converted to products. The height of the barrier is called as activation energy (Ea). Thus the reactant molecules transform to products only if they possess energy equal to or greater than such activation energy. A fraction of molecules those possess energy greater than Ea is given by f = e-Ea/RT.
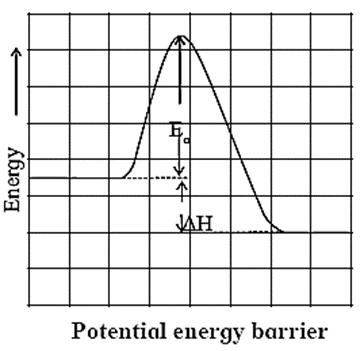
As a result only a few collisions lead to products.
Temperature dependence of reaction rates :
The concentrations change only a little with temperature. The rate constant shows a strong dependence on the temperature.
Arrhenius equation:
The fraction (t) of molecules at temperature T having activation energy Ea is given by f = e-Ea/RT.
If P represents the probability of Z collisions with proper orientation then,
Reaction rate = P x Z x e-Ea/RT
Hence the rate constant k of the reaction may be represented as
k = A X e-Ea/RT
where A is called frequency factor or pre-exponential factor and ΔH is the enthalpy change of the reaction. This equation is called Arrhenius equation.
Definitions :
Transition state or activated complex : The configuration of atoms formed from reactant molecules and which is at the peak of barrier in energy profile diagram having maximum potential energy compared to reactants and products is called transition state or activated complex.
Activation energy : The energy required to form activated complex or transition state from the reactant molecules is called activation energy. OR- The height of energy barrier in the energy profile diagram is called activation energy.
Obtaining Arrhenius equation :
From experimental observations of variation in rate constants with temperature, Arrhenius developed a mathematical equation between reaction rate constant (k), activation energy (Ed) and temperature T.
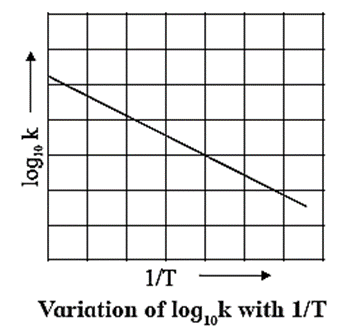
When a graph of in k is plotted against reciprocal of temperature (1 /T) a straight line with a negative slope is obtained. This is described by a mathematical equation as,
ln k = ln A − \(\frac{E_a}{RT}\)
= ln A − \(\frac{E_a}{RT}\) ln e … (‘.’ ln e = loge e = 1)
= ln A + \((\frac{E_a}{RT})\) ln e
= ln A + ln e-Ea/RT
∴ loge k = loge A + loge e-Ea/RT = loge A x e-Ea/RT
∴ 2.303 log10 k = 2.303 log10 A x e-Ea/RT
∴ log10 k = log10 A x e-Ea/RT
By taking antilogarithm,
k = A x e-Ea/RT
where k is a rate constant, R is the gas constant, Ea is activation energy, T is absolute temperature and the parameter A is called frequency factor or pre-exponential factor. This is Arrhenius equation.
Determination of activation energy :
Or Relation showing variation in rate constant with temperature :
By arrhenius equation, the rate constant k of the reaction at a temperature T is represented as,
k = A x e-Ea/RT
where A is a frequency factor, R is a gas constant and Ea is the energy of activation.
By taking logarithm to the base e, we get,
ln k = ln (A x e-Ea/RT)
= ln A + ln e-Ea/RT
= ln A \(-\frac{E_a}{RT}\) ln e
ln k = ln A −\(\frac{E_a}{RT}\)
2.303 log10 k = 2.303 log (A/10) \(-\frac{E_a}{RT}\)
∴ log10 k = log10 A \(-\frac{E_a}{2.303RT}\)
If k1 and k2 are the rate constants at temperatures T1 and T2 respectively, then
log10 k1 = log10 A \(-\frac{E_a}{2.303RT_1}\)
log10 k2 = log10 A \(-\frac{E_a}{2.303RT_2}\)
∴ log10 k2 − log10 k1 = [log10 A \(-\frac{E_a}{2.303RT_2}\) ] − [log10 A \(-\frac{E_a}{2.303RT_1}\)]
∴ log10 \(\frac{k_2}{k_1}\) = \(\frac{E_a}{2.303RT_1}\) \(-\frac{E_a}{2.303RT_2}\)
= \(\frac{E_a}{2.303R}[\frac{1}{T_1}-\frac{1}{T_2}]\)
log10 = \(\frac{E_a(T_2-T_1)}{2.303RT_1T_2}\)
By measuring the rate constants k1 and k2 at two different temperatures T1 and T2, the energy of activation Ea of the reaction can be obtained.
Graphical determination of activation energy :
By Arrhenius equation,
Rate constant = k = A x e-Ea/RT
where A is a frequency factor.
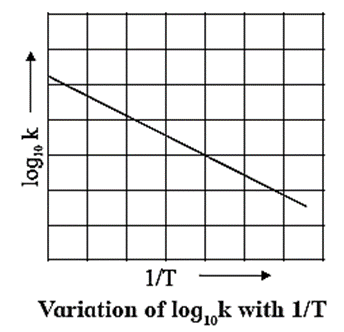
∴ ln k = ln A − \(\frac{E_a}{RT}\)
2.303 log10 k = 2.303 log10 A − \(\frac{E_a}{RT}\)
∴ log10 k = log10 A − \(\frac{E_a}{2.303RT}\)
∴ log10 k = − \((\frac{E_a}{RT})×\frac{1}{T}\) + log10 A …( y = −mx + c)
When log10 k is plotted against 1/T a straight line with negative slope is obtained. From the slope of the graph, energy of activation Ea, is obtained as follows :
Slope = \(\frac{E_a}{2.303R}\)
∴ Ea = 2.303 R x Slope
Graphical description of effect of temperature :
- It has been observed that the rates of chemical reactions increase as temperature increases.
- As the temperature increases, the kinetic energy of the molecules increases as well. The fraction of molecules with the lowest energy barrier, i.e. activation energy Ea, increases as temperature rises.
- As a result, the fraction of colliding molecules with kinetic energy (Ea) increases, and the rate of the reaction increases as temperature increases.
- The figure below shows that the area representing the fraction of molecules with kinetic energy greater than Ea is larger at higher temperatures T2 than at lower temperatures T1. This explains why the rate of the reaction increases as temperature rises.
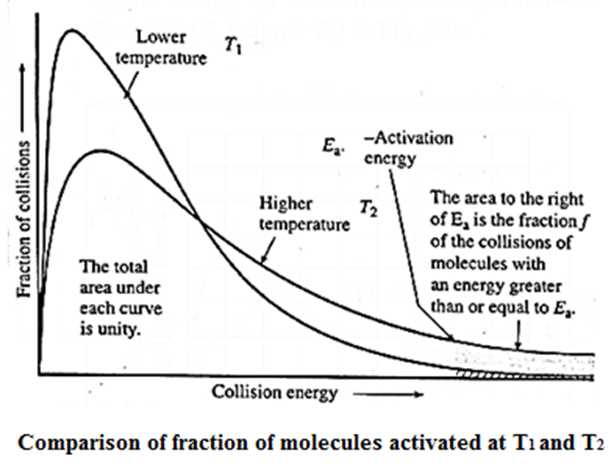
- The shaded area to the right of activation energy Ea represents fraction of collisions of activated molecules having energy Ea or greater.
Effect of a catalyst on the rate of reaction :
A catalyst is a substance, when added to the reactants, increases the rate of the reaction without being consumed.
For example, the decomposition of KClO3 in the presence of small amount of MnO2 is very fast but very slow in the absence of MnO2.
2KClO3(s) \(\underrightarrow{MnO_2+Δ}\) 2KCl(s) + 3O2(g)
- The phenomenon of catalysed reaction is called catalysis and depends on nature of the catalyst. In heterogeneous catalysis, the reactant molecules are adsorbed on the solid catalyst surface while in case of homogeneous catalysis, the catalyst reacts with one of the reactants, forms intermediate and decomposes reforming original catalyst and the products.
- The catalyst provides alternative and lower energy path or mechanism for the reaction.
- In the presence of the catalyst, the activation energy of the reaction is lowered. The height of activation energy barrier is less than that in the uncatalysed reaction.
- Due to lowering of energy of activation, (Ea) the number of molecules possessing Ea increases, hence the rate of the reaction increases.
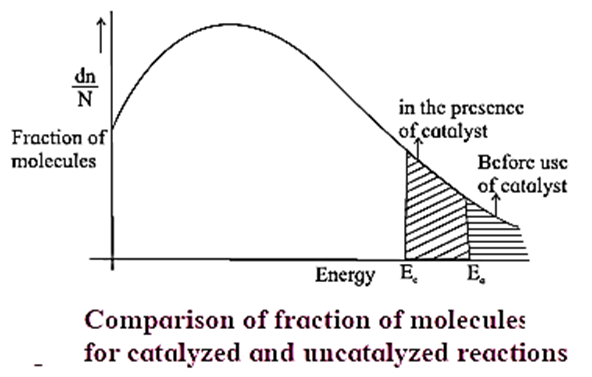
- The rate constant = k = A x e-Ea/RT where A is a frequency factor and hence the rates of the catalyzed reaction are higher than those of uncatalysed reactions.
- The catalyst does not change the extent of the reaction but hastens the reaction.
- The catalyst enters the reaction but does not appear in the balanced equation since it is consumed in one step and regenerated in another.
Difference between catalyst and reaction intermediate :
| Catalyst | Reaction intermediate |
| A catalyst accelerates the rate of reaction, | Reaction intermediate has no effect on the rate of the reaction. |
| Always present at the start of the
reaction |
Produced during the mechanism of the reaction. |
| A catalyst is consumed in one of the steps of mechanism and regenerated in a subsequent step | Reaction intermediate is formed in one step and consumed in subsequent step. |
| The catalyst is stable | The reaction intermediate is unstable and short lived. |
Chapter-6-Chemical Kinetics-Text Book
Chapter-6-Chemical Kinetics- Notes
Chapter-6-Chemical Kinetics- Solution
All 16 Chapters Notes -Class-12-Chemistry (16-PDF) Rs.137-Buy
Main Page : – Maharashtra Board Class 12th-Chemistry – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-5-Electrochemistry – Online Notes
Next Chapter : Chapter-7-Elements of Groups 16, 17 and 18 – Online Notes
We reply to valid query.