Circle
Class-10-Mathematics-2-Chapter-3-Maharashtra Board
Notes-Part-2
Topics to be learn : Part -2
|
Inscribed angle :
In the below figure, C is the centre of the circle. Point D lies on the circle. The arms of ∠ ADB intersect the circle at points A and B. Such an angle is called an Inscribed angle.
In the figure ∠ ADB is inscribed in arc ADB
Intercepted arc :

- In each of these above figure, the arc of a circle that lies in the interior of the ∠ ABC is an arc intercepted by the ∠
- The points of intersection of the circle and the angle are end points of that intercepted arc.
- Each side of the angle has to contain an end point of the arc.
- In figures (i), (ii) and (iii) only one arc is intercepted by that angle; and in (iv), (v) and (vi), two arcs are intercepted by the angle.
- Also note that, only one side of the angle touches the circle in (ii) and (v), but in (vi) both sides of the angle touch the circle.
Observe below figure arm BC does not contain any endpoint of the arc, hence arc is not intercepted by ∠ ABC in this case.
Inscribed angle theorem :
Statement : The measure of an inscribed angle is half of the measure of the arc intercepted by it.
Given : In a circle with centre O, ∠ BAC is inscribed in an arc BAC. ∠ BAC intercepts arc BXC of the circle.
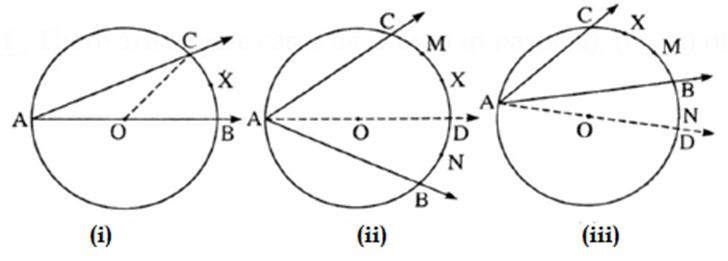
To prove : m∠ BAC = \(\frac{1}{2}\) m(arc BXC).
Proof : There arise three cases as shown in parts (i), (ii), (iii) of the figure.
Case l : The centre is on the angle [as in figure (i)]
In this case, join C to O.
Δ OAC is isosceles with OA = OC.
Let m∠ OAC = m∠ OCA = p,
By remote interior angles theorem,
m∠ BOC = m∠ OAC + m∠ OCA
m∠ BOC = p + p = 2p = 2m∠ BAC.
∴ m∠ BAC = \(\frac{1}{2}\) m∠ BOC
But m∠ BOC = m(arc BXC) (Definition of measure of minor arc)
∴ m∠ BAC = \(\frac{1}{2}\) m(arc BXC).
Case 2 : The centre is in the interior of the angle [as in figure (ii)]
In this case let D be the other end point of the diameter drawn through A.
Let are CMD be the one intercepted by ∠ CAD, and let arc BND be the one intercepted by ∠ DAB.
Then as proved in the first situation, we have
m∠ CAD = \(\frac{1}{2}\) m(arc CMD)
and m∠ DAB = \(\frac{1}{2}\) m(arc BND)
∴ m∠ CAD + m∠ DAB = \(\frac{1}{2}\) m(arc CMD ) + \(\frac{1}{2}\) m(arc BND)
∴ m∠ BAC = \(\frac{1}{2}\) [m(arc CMD) + m(arc BND)] = \(\frac{1}{2}\) m(arc BXC).
Case 3 : The centre is in the exterior of the angle [as in figure (iii)].
Again let D be the other endpoint of the diameter drawn through A.
Let arc CMD be the one intercepted by ∠ CAD and let arc BND be the one intercepted by ∠ DAB.
Then as proved in the first situation, we have,
m∠ CAD = \(\frac{1}{2}\) m(arc CMD) and m∠ DAB = \(\frac{1}{2}\) m(arc BND)
∴ m∠ CAD — m∠ DAB = \(\frac{1}{2}\) m(arc CMD) — \(\frac{1}{2}\) m(arc BND)
∴ m∠ BAC = \(\frac{1}{2}\) [m(arc CMD) − (arc BND)] = \(\frac{1}{2}\) m(arc BXC).
∴ The above theorem can also be stated as follows.
The measure of an angle subtended by an arc at a point on the circle is half of the measure of the angle subtended by the arc at the centre.
Corollaries of inscribed angle theorem :
Statement : Angles inscribed in the same arc are congruent.

Given : (i) A circle with centre C (ii) ∠ PQR and ∠ PSR are inscribed in arc PQR and intercepts arc PTR.
To prove : ∠ PQR ≅ ∠ PSR.
Proof:
∠ PQR = \(\frac{1}{2}\) m(arc PTR) ….(1).. (Inscribed angle theorem)
∠ PSR = \(\frac{1}{2}\) m(arc PTR) ……(2) .... (Inscribed angle theorem)
From (1) and (2), We get, ∠ PQR ≅ ∠ PSR.
Statement : Angle inscribed in a semicircle is a right angle.
Given : (i) A circle with centre O. (ii) seg AC is the diameter (iii) ∠ ABC is inscribed in arc ABC and intercepts arc AMC.
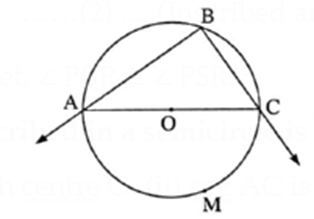
To prove : ∠ ABC = 90°
Proof :
m(arc AMC) = 180° ….. (Measure of a semicircle is 180°) …(1)
∠ ABC = \(\frac{1}{2}\) m(arc AMC) …….(Inscribed angle theorem)
∴ ∠ ABC = \(\frac{1}{2}\) × 180° …….[From (1)1
∴ ∠ ABC = 90°.
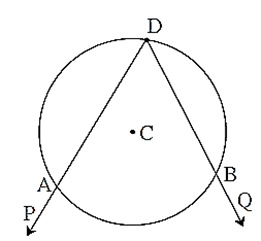
Cyclic quadrilateral :
If all vertices of a quadrilateral lie on the same circle then it is called a cyclic quadrilateral.
In the figure, points A, B, C and D lie on the same circle. c ABCD is cyclic.
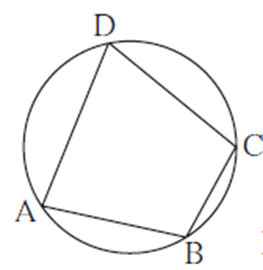
Theorem: Opposite angles of a cyclic quadrilateral are supplementary.
Given : c ABCD is cyclic.
To prove : ∠ DAB + ∠ DCB = 180°, ∠ ABC + ∠ ADC = 180°
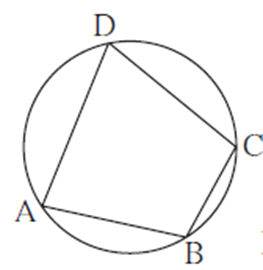
Proof : ∠ DAB is inscribed in arc DAB and intercepts arc DCB.
∴ ∠ DAB = \(\frac{1}{2}\) m(arc DCB) ……… (Inscribed angle theorem) ….(1)
∠ DCB is inscribed in arc DCB and intercepts arc DAB.
∴ ∠ DCB = \(\frac{1}{2}\) m(arc DAB) …… (Inscribed angle theorem) ….(2)
Adding (1) and (2), we get,
∠ DAB + ∠ DCB = \(\frac{1}{2}\) m(arc DCB) + \(\frac{1}{2}\) m(arc DAB)
∴ ∠ DAB + ∠ DCB = \(\frac{1}{2}\) [m(arc DCB) + m(arc DAB)]
Arc DCB and arc DAB constitute a complete circle
∴ ∠ DAB + ∠ DCB = \(\frac{1}{2}\) × 360° …..(Measure of a circle is 360°)
∴ ∠ DAB + ∠ DCB = 180°
Similarly, we can prove, ∠ ABC + ∠ ADC = 180°.
Corollary of cyclic quadrilateral theorem :
Statement : An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle.
Given : c ABCD is cyclic. ∠ DCE is an exterior angle of c ABCD.
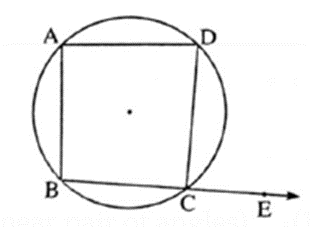
To prove : ∠ DCE ≅ ∠ BAD
Proof :
∠ DCE + ∠ BCD = 180° ………(Linear pair of angles) …(1)
c ABCD is cyclic.
∴ ∠ BAD + ∠ BCD = 180° ……… (Theorem of cyclic quadrilateral) … (2)
∴ from (1) and (2), We get,
∠ DCE + ∠ BCD = ∠ BAD + ∠ BCD
∴ ∠ DCE = ∠BAD
∴ ∠ DCE ≅ ∠ BAD.
Converse of cyclic quadrilateral theorem :
Theorem : If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic.
Given : In c ABCD, ∠ DAB + ∠ BCD = 180°.
To prove : c ABCD is cyclic.
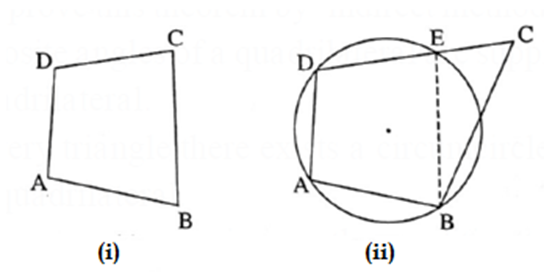
Proof : There is one and only one circle that passes through three non-collinear points.
∴ A circle passes through D, A and B. Let us assume that the fourth vertex C does not lie on the circle.
∴ it lies either in the interior or in the exterior of the circle.
Suppose C lies in the exterior of the circle, let E be the point where line DC intersects the circle. Draw scg BE
c ABED is cyclic. …..(By definition)
∠ DAB + ∠BED = 180° …..(By theorem of cyclic quadrilateral) …(1)
But ∠ DAB + ∠ DCB = 180° ……..(Given) …(2)
∴ ∠ DAB + ∠ BED = ∠ DAB + ∠ DCB …. [From (1) and (2)]
∴ ∠ BED = ∠ DCB ………(3)
But ∠ BED is an exterior angle of Δ BCE
∠ BED > ∠ DCB …….(Exterior angle theorem)
This contradicts statement (3).
∴ point C cannot lie in the exterior of the circle.
Similarly, it can be shown an assumption of C in the interior of the circle also leads to contradiction.
∴ C cannot lie in the interior of the circle
∴ point C has to lie on the circle.
∴ points A, B, C and D lie on the same circle.
∴ c ABCD is cyclic.
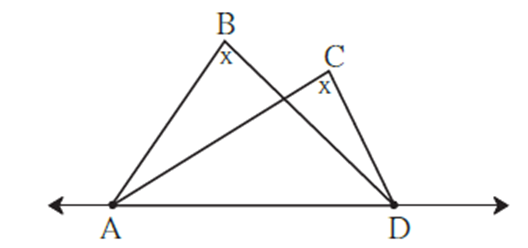
Theorem: If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic.
Given : Points B and C lie on the same side of line AD such that ∠ ABD ≅ ∠ ACD.
To prove : Points A, B, C, D are concyclic.
Proof : There is one and only one circle that passes through three non-collinear points.
∴ a circle passes through points A, B and D.
Let us assume that the fourth point R does not lie on the circle.
∴ it lies either in the interior or in the exterior of the circle.
Let us assume that point C lies in the exterior of the circle. Let seg AC intersect the circle at point T. Draw seg DT.
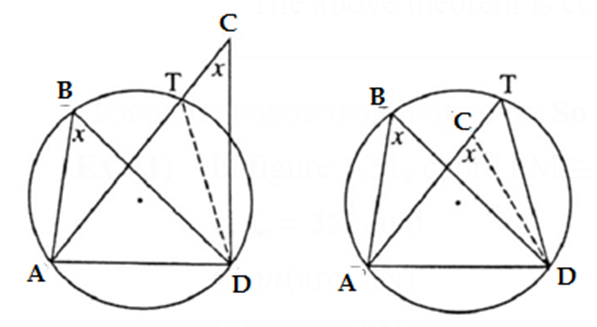
∠ ABD ≅ ∠ ACD ……..(Given) (1)
∠ ABD ≅ ∠ ATD ….(Angles inscribed in the same arc are congruent) ..(2)
∴ ∠ ACD ≅ ∠ ATD ….[From (1) and (2)] ….(3)
∠ ATD is an exterior angle of Δ TCD
∠ ATD > ∠ TCD ……(Exterior angle theorem)
i.e. ∠ ATD > ∠ ACD …..(A-T-C)
This contradicts (3)
∴ our assumption is false.
∴ point C cannot lie outside the circle.
Let us assume that point C lies in the interior of the circle.
Produce AC to intersect the circle in the point T. Draw DC.
∠ ABD ≅ ∠ ATD ….(4) … (Angles inscribed in the same arc are congruent)
But ∠ ABD ≅ ∠ ACD …..(Given) ….(5)
from (4) and (5),
∠ ATD ≅ ∠ ACD ……(6)
∠ ACD is an exterior angle of Δ CTD,
∠ ACD > ∠ CTD ……(Exterior angle theorem)
i.e. ∠ ACD > ∠ ATD ….(A-C-T)
This contradicts (6)
∴ point C cannot lie inside the circle.
∴ point C lies on the circle.
points A, B, C and D are concyclic.
[Note : The above theorem is the converse of ‘Angles inscribed in the same arc are congruent’.]
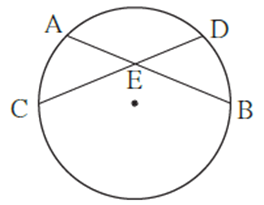
Q. If two chords of a circle intersect each other in the interior of a circle then the measure of the angle between them is half the sum of measures of arcs intercepted by the angle and its opposite angle.
Prove the statement.
Given : (i) A circle with centre O. (ii) Chord AB and chord
CD intersect at point E inside the circle.
To prove : ∠ CEB = \(\frac{1}{2}\) [m(arc AD) + m(arc CB)]
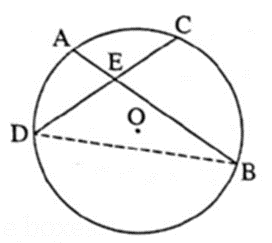
Draw seg BD ∠ ABD = \(\frac{1}{2}\) m(arc AD) …..(1) ….(Inscribed angle theorem) ∠ CDB = \(\frac{1}{2}\) m(arc CB) …..(2) ….(Inscribed angle theorem) ∠ CEB is an exterior angle of Δ EDB. ∠ CEB = ∠ EBD + ∠ EDB ….. (Remote interior angles theorem‘) i.e. ∠ CEB = ∠ ABD + ∠ CDB …..(A—E—B and C—E—D) ∴ ∠ CEB = \(\frac{1}{2}\) m(arc AD) + m(arc CB) ……[From (1) and (2)] ∴ ∠ CEB = \(\frac{1}{2}\) [m(arc AD) + m(arc CB)]
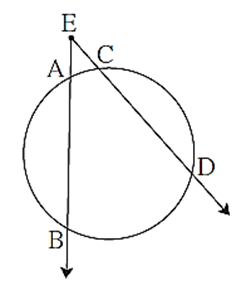
Q. If two lines containing chords of a circle intersect each other outside the circle, then the measure of angle between them is half the difference in measure of the arcs intercepted by the angle. Prove the statement.
Given : (i) A circle with centre O.
(ii) Line AB intersects the circle at points A and B
(iii) Line CD intersects the circle at points C and D
(iv) Lines AB and CD intersect at point E.
To prove = ∠ AEC = \(\frac{1}{2}\) [mere Ac) − m(arc BD)]
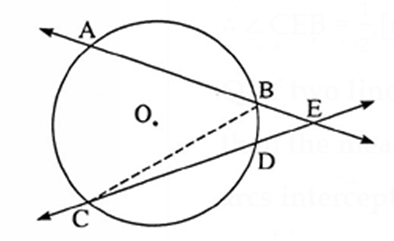
Draw seg BC ∠ ABC = \(\frac{1}{2}\) m(arc AC) …..(1) ….(Inscribed angle theorem) ∠ BCD = \(\frac{1}{2}\) m(arc BD) …..(2) ….(Inscribed angle theorem) ∠ ABC is an exterior angle of Δ BEC. ∠ ABC = ∠ BEC + ∠ BCE ….. (Remote interior angles theorem‘) i.e. ∠ ABC = ∠ AEC + ∠ BCD …..(A—B—E and C—D—E) ∴ m(arc AC) = ∠ AEC + \(\frac{1}{2}\) m(arc BD) ……[From (1) and (2)] ∴ ∠ AEC = \(\frac{1}{2}\) [m(arc AC) − m(arc BD)]
| Remember :
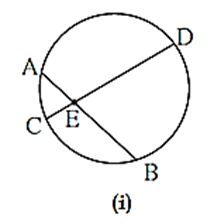
(i) Inscribed Angle theorem : The measure of an inscribed angle is half the measure of the arc intercepted by it. · Corollary 1 : Angles inscribed in the same arc are congruent. · Corollary 2 : Angle inscribed in a semicircle is a right angle. (ii) Theorem of cyclic quadrilateral: Opposite angles of cyclic quadrilateral are supplementary. Corollary of cyclic quadrilateral theorem : An exterior angle of cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle. (iii) Converse of cyclic quadrilateral theorem: If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic. (iv) If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic. (v) In the figure, chords AB and CD intersect at point E inside the circle, then (a) ∠ AEC = \(\frac{1}{2}\) [m(arcAC) + m(arc DB)] (b) Ð CEB= \(\frac{1}{2}\) [m(arc AD) + m(arc CB)]
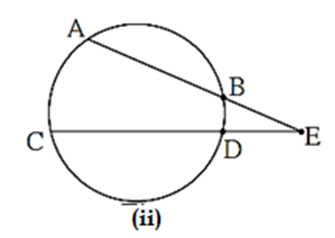
(vi) In the figure, line AB and CD intersect at point E outside the circle, then ∠ BED = \(\frac{1}{2}\) [m(arc BD) − m(arc AC)]
|
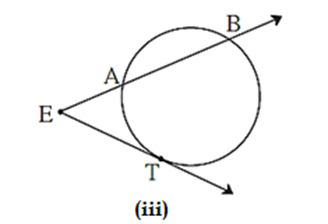
Theorem of angle between tangent and secant :
Theorem : If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc.
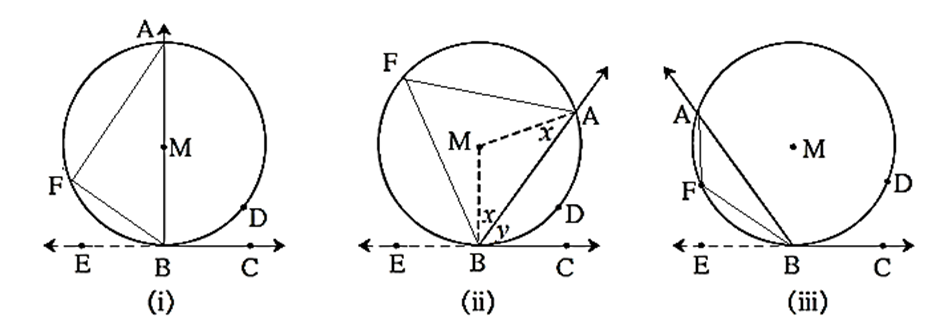
Given : Let M be the centre of the circle. Line EBC is tangent to the circle at point B. Seg BA is a chord of the circle. Point D of the circle is on C side of line BA and point F of the circle is on E side of line BA.
To Prove = m∠ ABC = \(\frac{1}{2}\) m(arc ADB).
Proof : Considering ∠ ABC and the arc ADB intercepted by it, we see from the figures that arc ADB may be a semicircle, may be a minor arc or may be a major arc. We deal with these cases separately.
Case-1: When ∠ ABC intercepts a semicircle, [as in figure (i)] the chord BA passes through the centre.
In that case, ∠ ABC = 90° …….(Tangent theorem)
Also since m(arc BDA) = 180°
∴ \(\frac{1}{2}\) m(arc BDA) = \(\frac{1}{2}\) × 180° = 90°
∴ m∠ ABC = \(\frac{1}{2}\) m(arc ADB)
Case-2: When ∠ ABC intercepts a minor arc, [as in figure (ii)] the centre lies in the exterior of ∠ ABC.
We have, m∠ ABC = 90° — m∠ ABM
m∠ ABM = 90° — m∠ ABC
m∠ BAM = 90° — m∠ ABC ……( Δ ABC is isosceles)
m∠ ABM + m∠ BAM = 180° — 2m∠ ABC
180° — m∠ BMA = 180° — 2m∠ ABC
∴ m∠ BMA = 2m∠ ABC.
But m∠ BMA = m(arc ADB)
∴ m∠ ABC = \(\frac{1}{2}\) m(arc ADB)
Case-3: When ∠ ABC intercepts a major arc [as in figure (iii)] the centre lies in the interior of ∠ ABC.
We then have ∠ DBA intercepting a minor arc BFA
m∠ DBA = \(\frac{1}{2}\) m(arc BFA)
180° — m∠ ABC = \(\frac{1}{2}\) [360° − m(arc ADB)]
= 180° — \(\frac{1}{2}\) m(arc ADB)
∴ m∠ ABC = \(\frac{1}{2}\) m(arc ADB)
Thus, in every case,
m∠ ABC = \(\frac{1}{2}\) m(arc ADB)
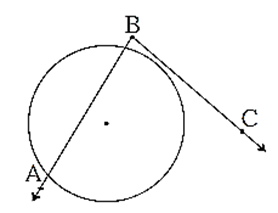
Alternative statement of the above theorem :
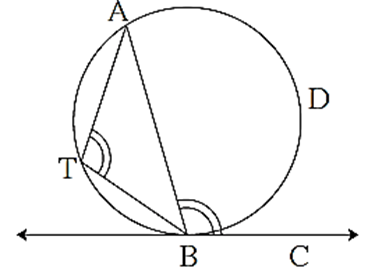
In the adjacent figure , line AB is a secant and line BC is a tangent. The arc ADB is intercepted by ∠ ABC. Chord AB divides the circle in two parts. These are opposite arcs of each other.
Now take any point T on the arc opposite to arc ADB
From the above theorem, m∠ ABC = \(\frac{1}{2}\) m(arc ADB) = ∠ ATB.
∴ the angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
Converse of theorem of the angle between tangent and secant
Statement: A line is drawn from one .end point of a chord of a circle and if the angle between the chord and the line is half the measure of the are intercepted by that angle, then that line is a tangent to the circle.
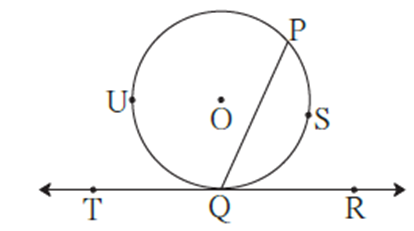
In the figure, if ∠ PQR = \(\frac{1}{2}\) m(arc PSQ) or ∠ PQT = \(\frac{1}{2}\) m∠ PUQ then line TR is tangent to the circle.
This property is used in constructing a tangent to the given circle.
Theorem of internal division of chords :
Statement : Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
Given : (i) A circle with centre O. (ii) Chords PR and QS intersect at point E inside the circle.
To prove : PE x ER = QE × ES.
Construction : Draw seg PQ and seg RS.
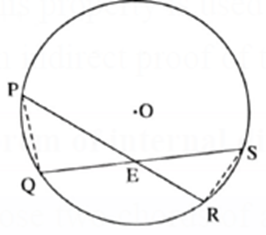
Proof :
∠ PQS ≅ ∠ SRP ….(Angles inscribed in the same arc are congruent)
i.e. ∠ PQE ≅ ∠ SRE ….(P—E—R and Q—E—S) …(1)
In Δ PQE and Δ SRE,
∠ PQE ≅ ∠SRE …..[From (1)]
∠ PEQ ≅ ∠ SER …..(Vertically opposite angles)
∴ Δ PQE ~ Δ SRE .....(AA test of similarity)
∴ \(\frac{PE}{SE}=\frac{QE}{RE}\) ……(Corresponding sides of similar triangles are in proportion)
∴ PE × ER = QE × SE.
In above figure point E divides the chord PR into segments PE and ER.
PE × ER is the area of a rectangle having sides PE and ER. Similarly E divides QS into segments QE and ES. QE × ES is the area of a rectangle of sides QE and ES. We have proved that PE × ER = QE × ES.
So the above theorem can be stated as : If two chords of a circle intersect in the interior of a circle then the area of the rectangle formed by the segments of one chord is equal to the area of similar rectangle formed by the other chord.
Theorem of external division of chords :
Statement: If secants containing chords AB and CD of a circle intersect outside the circle in point E, then AE × EB = CE × ED.

Given : (i) A circle with centre O. (ii) Secants AB and CD intersect at point E outside the circle.
To prove = AE × EB = CE × DE.
Construction : Draw seg AD and seg BC.
Proof :
∠ DAB ≅ ∠BCD …..(Angles inscribed in the same arc are congruent)
i.e. ∠ DAE ≅ ∠ BCE ……(A—B—E and C—D—E) ….(1)
In Δ ADE and Δ CBE,
∠ DAE ≅ ∠ BCE …..[From (1)]
∠ AED = ∠ CEB ……(Common angle)
∴ Δ ADE ~ Δ CBE …. (AA test of similarity)
∴ \(\frac{AE}{CE}=\frac{DE}{BE}\) ……(Corresponding sides of similar triangles are in proportion)
∴ AE × BE = CE × DE.
Tangent secant segments theorem :
Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA × EB = ET2.
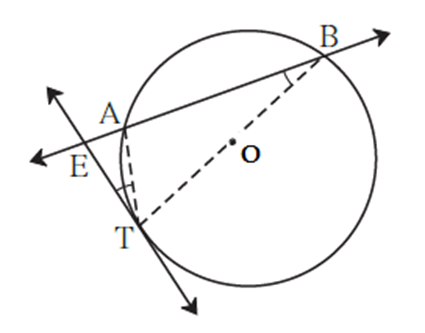
Given : (i) A circle with centre O.
(ii) Tangent ET touches the circle at point T.
(iii) Secant EAB intersects the circle at points A and B.
To prove : EA × EB = ET2.
Construction : Draw seg TA and seg TB.
Proof : In Δ ETA and Δ EBT,
∠ AET ≅ ∠ TEB ….(Common angle)
∠ ETA ≅ ∠ EBT …..(Tangent secant theorem)
Δ ETA ~ Δ EBT …..(AA test of similarity)
∴ \(\frac{ET}{EB}=\frac{EA}{ET}\) ……(Corresponding sides of similar triangles are in proportion)
∴ EA × EB = ET × ET .
∴ EA × EB = ET2.
| Remember :
(i) In figure AE × EB = CE × ED This property is known as theorem of chords intersecting inside the circle.
(ii) In figure AE × EB = CE × ED This property is known as theorem of chords intersecting outside the circle.
(iii) In figure EA × EB = ET2 This property is known as tangent secant segments theorem.
|
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-2-Pythagoras Theorem – Online Notes
Next Chapter : Chapter-4-Geometric Construction – Online Notes