Dual Nature of Radiation and Matter
Maharashtra Board-Class-12th-Physics-Chapter-14
Notes-Part-2
Topics to be Learn : Part-2
|
Wave-Particle Duality of Electromagnetic Radiation:
Explanation : A particle is a definite position in space at a given instant that has mass (or momentum), whereas a wave is a periodically repeated pattern in space and time that is generally described by its propagation velocity, wavelength, and amplitude. A wave is distinguished by the fact that it is not localised, but rather spreads across a region. As a result, these two concepts are incompatible, and classical physics treats particles and waves separately.
Under suitable circumstances, light and all other types of electromagnetic radiation exhibit typical wave phenomena like polarization, interference and diffraction.
On the other hand, radiation exhibits a particle-like nature when it interacts with matter, as in the photoelectric effect and the Compton effect (scattering of X-rays by electrons in matter).
It is emitted or absorbed only in terms of quanta of energy. This is the concept of photon: a particle with energy E = hv, where v is the frequency of the radiation and Planck's constant h connects v and E, respectively the wave and particle aspects.
We see, therefore, that radiation exhibits a dual character. The synthesis of these two contradictory descriptions is called wave—particle duality of electromagnetic radiation.
| Know This :
The particle nature of radiation is seen in black body radiation and photoelectric effect. In the former, near room temperature, the radiation is mostly in the infrared region while in the latter it is in the visible and ultraviolet region of the spectrum. The third experiment, which established that a photon possesses momentum like a particle, was Compton scattering where X-rays and γ-rays interact with matter. In 1923, A. H. Compton made a monochromatic beam of X-rays, of wavelength λ, incident on a graphite sheet and measured the intensity of the scattered rays in different directions as a function of wavelength. He found that although the incident beam consisted of a single wavelength λ, the scattered intensity was maximum at two wavelengths. One of these was same as the incident wavelength but the other λ′ was larger by an amount Δλ. Δλ is known as the Compton shift that depends on the scattering angle. Compton explained his observations by considering incidence of X-ray beam on graphite as collision of X-ray photons with the electrons of graphite, like collision of billiard balls. Energy and momentum is transferred during the collision and scattered photons have lower energy than the incident photons. Therefore they have lower frequency or higher wavelength. The Compton shift is given by the relation Δλ = λ’ – λ = \(\frac{h}{m_ec}(1-cos\,θ)\) where θ is the scattering angle. The shift depends only on the scattering angle and not on the incident wavelength. This shift cannot be explained using wave theory. If we let the Planck’s constant go to zero, we get the result expected from wave theory. This is the test to check whether the new picture is correct or not. |
Compton effect :
When a high energy X-ray photon or y-ray photon is scattered by an electron that is (almost) free, the photon loses energy and the electron gains energy (see Fig.).
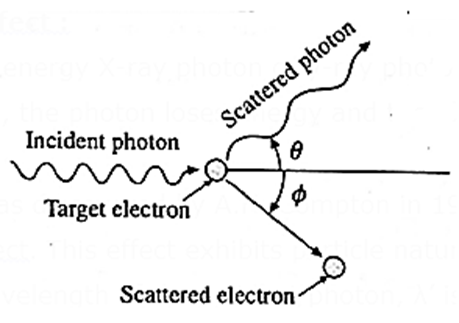
This effect was discovered by A.H. Compton in 1923. It is now known as the Compton effect. This effect exhibits particle nature of electromagnetic radiation.
If λ is the wavelength of the incident photon, λ’ is the wavelength of the scattered photon, θ is the angle through which the photon is scattered, m0 is the rest mass of an electron, c is the speed of light in free space and his Plank’s constant, then, the wavelength shift, called the Compton shift is given by
λ’ – λ = \(\frac{h}{m_0c}(1-cos\,θ)\)
(λ’ – λ)max = \(\frac{h}{m_0c}[1-(-1)]\) for θ = 1800
= \(\frac{6.63×10^{-34}(2)}{(9.1×10^{-34})(3×10^8)}\) = 4.857 x 10−12 m
= 4.857 x 10−2 Å = 4.857 x 10−3 nm
Inverse Compton effect : In a collision between a low energy photon and a high energy electron, scattering results in loss in the energy of the electron and gain in the energy of the photon. This effect is known as the inverse Compton effect.
Significance of the photoelectric effect :
- The phenomena of interference and polarization exhibit the wave nature of light, and James Clerk Maxwell (1831—79), British physicist, had established by 1865 that light is, and propagates as, an electromagnetic wave.
- In his interpretation of the photoelectric effect in 1905, Einstein proposed that electromagnetic radiation behaves as a series of small packets or quanta of energy, later called photons. If the frequency of radiation is v, each Photon has energy hv and momentum hv/c, where c is the speed of light in free space Einstein's photoelectric equation was verified experimentally by Robert Andrews Millikan (1868-1953), US physicist, in 1916.
- A very strong additional evidence in support of the quantum theory of radiation was the discovery (in 1923) and explanation of the inelastic scattering of X—rays or y-rays by electrons in matter by Arthur Holly Compton (1892-1962), US physicist. This inelastic scattering in which a photon transfers part of its energy to an electron is known as the Compton effect. It is similar to the Raman effect. The Compton effect shows particle nature of electromagnetic radiation.
- Since energy and momentum are considered in classical physics as characteristic properties of particles, the photoelectric effect and Compton effect exhibit the particle nature of radiation. But, to describe the photon energy, the quantum theory needs the frequency of the radiation, which is necessarily an attribute associated with a wave in classical physics. Thus, radiation exhibits the dual, seemingly contradictory, characters of particle and wave. In an experiment, we need to use only one of the descriptions, not both at the same time.
Summary of the quantum theory of radiation (Photon picture of electromagnetic radiation) :
- In its interaction with matter, electromagnetic radiation behaves as particles or quanta of energy.
- A quantum of energy is called a photon.
- If the frequency of radiation is v, irrespective of the intensity of radiation, each photon has energy hv and momentum hv/c, where c is the speed of light in free space.
- Intensity of radiation corresponds to the number of photons incident per unit time per unit surface area.
- Photons are electrically neutral and have zero rest mass.
- A photon-particle collision (such as photon-electron collision) obeys the principles of conservation of energy and momentum. However, in such a collision, an incident photon may be absorbed and/ or a new photon may be created, so that the number of photons may not be conserved. For example, a y-ray photon of energy greater than 1.02 MeV can produce an electron-positron pair in the presence of a heavy nucleus such as lead. In this case, the photon disappears and two particles (electron and positron) are produced. The total energy and momentum are conserved.
Photo Cell:
A photocell or photoelectric cell is a device in which light energy is converted into electrical energy by photoelectric effect.
Construction : One type of photoelectric cell, depicted in Fig., consists of a highly evacuated or gas—filled glass tube, an emitter (cathode), and a collector (anode).
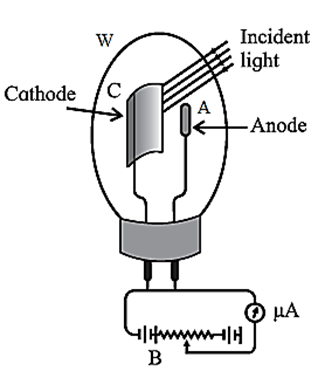
The light enters through a quartz window W and strikes the semi-circular cathode C, which is coated with a photosensitive metal. The anode is a straight wire of platinum or nickel that is coaxial with the cathode.
If the cell is required to respond to the visible part of the spectrum, the cathode is coated with potassium or rubidium and the quartz window is replaced by glass. If the UV radiation only is to be used, cadmium is used as the sensitive surface. The cell is either highly evacuated (for accurate photometry) or filled with an inert gas at low pressure (if a larger current is desired).
Working :
- A photocell is connected in series with a battery and a variable resistance.
- The collector is kept at a positive potential with respect to the emitter.
- When UV radiation or visible light of frequency greater than the threshold frequency for the emitter surface is incident on the emitter, the ejected photoelectrons are focused by the cylindrical emitter (cathode) towards the collector (anode).
- The photoelectrons collected by the collector constitute a photocurrent which may be measured by a microammeter in series with the photocell, as in an exposure meter or lux meter.
- Otherwise, the photocurrent is used to operate a relay circuit as in an alarm, or to drive the coils of a speaker as in reading an optical sound track in a cine film. The photocurrent becomes zero when the incident light is cut off.
Applications of a photoelectric cell :
(i) In an exposure meter used for photography: A photographic film must be exposed to the correct amount of light, which is determined by the exposure time for a given film speed and lens aperture. A photocell, battery, and microammeter are connected in series to form an exposure metre. When the metre is pointed at an object, the reflected light enters the photocell, and the photocurrent is proportional to the intensity of the light. Typically, the microammeter scale is calibrated to directly read the exposure time.
(ii) As a lux meter ; A lux meter is used to measure the illumination and is similar in working to an exposure meter, except that the scale is calibrated to read the illumination in lux.
(iii)In a burglar alarm as a ‘normally closed’ light-activated switch : It consists of a photocell, battery, relay system and a small directed light source. The radiation from the source falls on the photocell. If the light beam is interrupted by an intruder, the photoelectric current stops. This activates the relay system which sets off an alarm.
(iv) In an optical reader of sound track in a cine film : The sound track of a cine film is recorded on one side of the positive film that is run in a cinema hall. The track consists of a dark wavy patch modulated by the recorded sound. Light from the projector lamp also passes through the sound track and falls on a photocell behind. The photocurrent is proportional to the transmitted light intensity and changes according to the recorded sound wave. The photocurrent is amplified and is used to drive the loudspeaker.
(v) A photocell can be used to switch on or off street lights.
De Broglie Hypothesis:
De Broglie hypothesis : The wave-particle duality may not be specific to light but rather a universal property of nature, according to French physicist Louis de Broglie (1892-1987), who proposed this in 1924. This means that a particle of matter in motion also has a wave or periodicity associated with it, which becomes apparent when the size of Planck's constant h cannot be disregarded.
De Broglie equation : A particle of mass m moving with a speed v should under suitable experimental conditions exhibit the characteristics of a wave of wavelength
λ = h/mv = h/p …..(1)
where p = mv E momentum of the particle.
The relation λ = h/p is called the de Broglie equation, and the wavelength λ associated with a particle momentum is called its de Broglie wavelength. The corresponding waves are termed as matter waves or de Broglie waves or Schrodinger waves.
Concept of de Broglie waves or matter waves :
- This dual character of matter contained in above Eq. (1) is usually referred to as the wave nature of matter or matter waves.
- They are a set of waves that represent the behaviour of particles under appropriate conditions. It does not, however, mean that the particles themselves are oscillating in space.
- Interpretation of matter waves by Max Born (1882—1970), German born British physicist, is that they are waves of probability, since the square of their amplitude at a given point is linked to the likelihood of finding the particle there. Hence, the wavelength λ may be regarded as a measure of the degree to which the energy is localized.
- If λ is exceedingly small, the energy is very localized and the particle character of the object is dominant. On the other hand, if λ is very large, the energy is distributed over a large volume; under these circumstances, the wave behaviour is dominant.
- The wave nature of material particles such as the electron, neutron and helium atom has been established experimentally beyond doubt.
Expression for the de Broglie wavelength :
For the particle-like aspects of electromagnetic radiation, we consider radiation to consist of particles whose motion is governed by the wave propagation properties of certain associated waves.
To determine the wavelength of such waves, consider a beam of electromagnetic radiation of frequency v whose quanta have energy E.
E = hv
where h is the Planck constant.
For a quantum of radiation of momentum p, by Einstein's theory,
E = pc
where c is the speed of propagation of the radiation in free space. .
∴ pc = hv
∴ \(p\frac{c}{v}\) = h
The wavelength λ of the associated wave governing the motion of the quanta is given by the relation
λ = c/v.
∴ pλ = h, ∴ λ = h/p
This is the required expression.
Expression for the de Broglie wavelength associated with an electron accelerated from rest through a potential difference V :
Consider an electron accelerated from rest through a potential difference V.
Let v be the final speed of the electron. We consider the nonrelativistic case,
v << c, where c is the speed of light in free space. The kinetic energy acquired by the electron is
½ mv2 = \(\frac{1}{2m}(mv)^2\) = ev …. (1)
where e and m are the electronic charge and mass (nonrelativistic).
Therefore, the electron momentum,
p = mv = \(\sqrt{2meV}\) ……(2)
The de Broglie wavelength associated with the electron is
λ = h/p …….(3)
where h is Planck's constant.
From Eqs. (2) and (3),
λ = \(\frac{h}{\sqrt{2meV}}\)
Equation (4) gives the required expression.
[Substituting the values of h=6.63 x 10−34 J.s, m = 9.1 x 10−31 kg, e= 1.6 x 10−19 C in Eq. (4), we obtain
λ = \(\sqrt{150/V}×10^{-10}m\) = \(\sqrt{150/V}\,Å\) =\(\frac{12.25}{\sqrt{V}}\,Å\)
where V is in volt. Therefore, electrons accelerated from rest through 150 volts have a de Broglie wavelength of 1 A. This corresponds to the X-ray region of the electromagnetic spectrum.]
Davisson and Germer experiment (1927) :
- The experimental arrangement, as shown in Fig. consists of an electron gun, a crystal holder and an electron detector enclosed in a vacuum chamber.
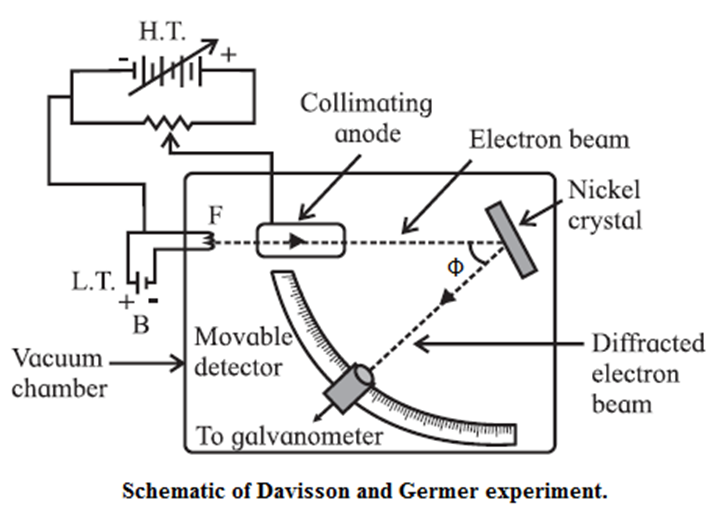
- In the electron gun, electrons emitted by a heated metallic filament (cathode) are accelerated by a potential difference V between the cathode and the anode, and emerge through a small hole in the anode. The electron gun directs a narrow collimated beam of electrons at a nickel crystal. Scattered electrons are detected by a movable detector.
- The angle Φ between the incident and scattered beams is the scattering angle. Polar graphs of the number of scattered electrons as a function of angle Φ are plotted for different values of the accelerating voltage.
It is found that the electrons are scattered at a certain angle more than at others. Also, the number of scattered electrons in this direction is maximum for a certain kinetic energy of the incident electrons.
The detector registered a maximum at a scattering angle Φ = 50° for V = 54 V. This electron diffraction can be understood only on the basis of de Broglie’s matter wave model. The de Broglie wavelength of the electrons accelerated from rest through a p.d. of 54V is λ = \(\sqrt{150/54}\,Å\) = 1.67 Å
The wavelength calculated from the diffraction effect is 1.65 Å, nearly 1.67 Å
Importance of Experiment : The Davisson and Germer experiment directly indicated the wave nature of material particles and quantitatively verified the de Broglie hypothesis for the existence of matter waves.
| Know This :
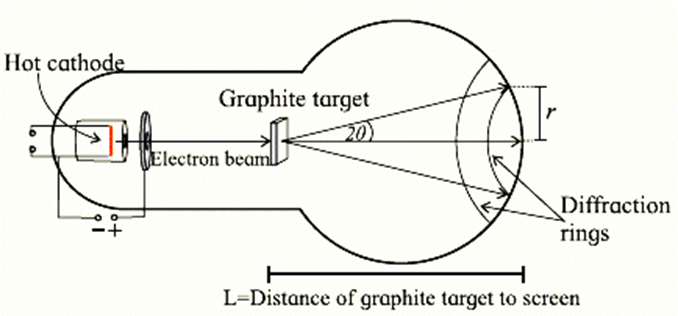
Diffraction results described above can be produced in the laboratory using an electron diffraction tube as shown in figure. It has a filament which on heating produces electrons. This filament acts as a cathode. Electrons are accelerated to quite high speeds by creating large potential difference between the cathode and a positive electrode. On its way, the beam of electrons comes across a thin sheet of graphite. The electrons are diffracted by the atomic layers in the graphite and form diffraction rings on the phosphor screen. By changing the voltage between the cathode and anode, the energy, and therefore the speed, of the electrons can be changed. This will change the wavelength of the electrons and a change will be seen in the diffraction pattern.
When the accelerating voltage is increased, the kinetic energy and hence the momentum of the electron increases. This decreases the de Broglie wavelength of the electron. Hence, the radius of the diffraction ring decreases. |
Wave-Particle Duality of Matter:
Depending upon experimental conditions or structure of matter, electromagnetic radiation and material particles exhibit wave nature or particle nature. This is known as wave-particle duality.
It applies to all phenomena. The wave nature and particle nature are liked by the de Broglie relation λ = h / p, where λ is the wavelength of matter waves, also called de Broglie waves/ Schrodinger waves, p is the magnitude of the momentum of a particle or quantum of radiation and h is the universal constant called Planck's constant.
| Know This:
We have seen earlier that electrons are bound inside a metal surface and need some minimum energy equal to the work function to be knocked off from the surface. This energy, if provided by any means, can make the electron come out of the metal surface. Physical ways to provide this energy differentiate the physical processes involved and accordingly different devices and characterizing microscopes based on them have been designed by scientists. • Thermionic emission : By heating to temperatures ~2000 ºC provide thermal energy. • Field emission : By establishing strong electric fields ~106 V/m at the surface of a metal tip, provide electrical energy. • Photo-electron emission : By shining radiation of suitable frequency (ultraviolet or visible) on a metal surface provide light energy. Electron microscope: You have learnt about resolving power and resolution of telescopes and microscopes that use the ordinary visible light. The resolution of a microscope is limited by the wavelength of the light used. The shorter the wavelength of the characterizing probe, the smaller is the limit of resolution of a microscope, i.e., the resolution of microscope is better. Better can be attained by illuminating the objects to be seen by radiation of smaller wavelengths. We have seen that an electron can behave as a wave and its wavelength is much smaller than the wavelength of visible light. The wavelength can be made much smaller as it depends on the velocity and kinetic energy of the electron. An electron beam accelerated to several keV of energy will correspond to de Broglie wavelength much smaller than an angstrom, i.e., λe<< 1×10-10 m. The resolution of this electron microscope will be several hundred times higher than that obtainable with an optical microscope. Other advantages of electron microscopes are that
It was proposed in 1925 that atoms in the solids can act as diffraction centers for electron waves and can give information about the geometry or structure of solid, just as X-rays do on getting diffracted by solids. However, it took many years to realize an electron microscope for practical applications. The first electron microscope was developed by Herald Ruska in Berlin, Germany in the year 1929. Microscopic objects, when illuminated using electron beams, yield high resolution images. Images of microscopic and nanometric objects and even of viruses have been obtained by scientists using electron microscopes, making valuable contributions to mankind. Transmission electron microscopy can resolve very small particles. A micrograph on the cover page of this book shows tiny crystals of dimensions less than 50 nm. An electron diffraction pattern is also seen on the cover page (spot pattern). When an electron beam passes through a crystal having periodic arrangement of atoms, diffraction occurs. The crystal acts as a collection of diffraction slits for the electron beam. |
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-13-AC Circuits –Online Notes Next Chapter :Chapter-15- Structure of Atoms and Nuclei – Online Notes
We reply to valid query.