Sound
Maharashtra Board-Class-11-Science-Physics-Chapter-8
Notes Part-1
|
Topics to be Learn : Part-1
|
Introduction :
Wave motion : Wave motion is the way that waves travel through a medium, such as air, water, or solid. It involves the transfer of energy and momentum from one point to another without moving any matter.
- There are different types of waves and not all types require material medium to travel through.
- A wave can be described by its amplitude, wavelength, frequency, speed, and direction
Types of waves:
(i) Mechanical waves: A wave is said to be mechanical if a material medium is essential for its propagation.
- Examples : Water waves, waves along a stretched string, seismic waves, sound waves, etc.
- Such a type of wave originates in the displacement of some portion of an elastic medium from its normal position. This causes the layers of matter to oscillate about their equilibrium positions.
- Because of the elastic properties of the material, the disturbance is transmitted from one layer to the next, and so the waveform progresses through the medium.
Explanation by example :
- Dropping a stone, for example, disturbs the peaceful surface of a pool of water. Then, a disturbance concentrated on that spot moves outward along the water's surface as a wave. A piece of paper or a chip of wood floating on the surface travels up and down as the wave passes, but it is not carried ahead with the wave.
- Figure shows a wave set up in a row of particles (of equal mass and connected elastically) by the displacement, and consequent vibration, of particle 1. The energy of particle 1 consists of both kinetic energy and potential energy. Particle 1 transmits its energy to particles 2, 3, etc., successively, and the wave form propagates as indicated.
(ii) EM waves: Periodic oscillations in electric and magnetic fields create EM waves. These waves can propagate via material media, although the medium is not required for their propagation.
(iii) Matter waves: If an item is in motion, it is always related with a wave. These are matter waves.
Common Properties of all Waves:
(i) Amplitude (A): Amplitude of a wave motion is the largest displacement of a particle of the medium through which the wave is propagating, from its rest position.
- SI unit of amplitude is the metre (m)
(ii) Wavelength (λ): It is the distance between consecutive particles of the medium which are moving in exactly the same way at the same time and have the same displacement from their equilibrium positions.
- SI unit of wavelength is the metre (m)
(iii) Period (T): Time required to complete one vibration by a particle of the medium is the period T of the wave.
- It is measured in seconds.
(iv) Double periodicity: Waves possess double periodicity.
- At every location the wave motion repeats itself at equal intervals of time, hence it is periodic in time.
- Similarly, at any given instant, the form of wave repeats at equal distances hence, it is periodic in space.
- In this way wave motion is a doubly periodic phenomenon i.e. periodic in time and periodic in space.
(v) Frequency (n): Frequency of a wave is the number of vibrations performed by a particle during each second.
- SI unit of frequency is hertz. (Hz)
Frequency is a reciprocal of time period, i.e., n = 1/T
(vi) Velocity (v): The distance covered by a wave per unit time is called the velocity of the wave.
- It is the magnitude of velocity of wave. SI Unit is metre per second (m/s)
Relation between the velocity (speed), wavelength and frequency of a wave :
During the passage of a progressive wave through a medium, the wave advances a
distance equal to the wavelength λ. in the periodic time T of the vibration of the particles of the medium. Then, the speed of propagation (the magnitude of the velocity) of the wave is
v = λ/T
The frequency n of the progressive wave is equal to the reciprocal of the period :
n = 1/T (2)
From Eqs. (1) and (2), we have,
v = n λ . i.e., wave speed = frequency x wavelength
This relation is true for all types of progressive wave.
Remember :
- Frequency and amplitude of a wave are determined by the source of waves.
- Frequency does not change when a wave travels from one medium to another.
- However, the wave speed, and correspondingly the wavelength, depend on the medium and change when the medium is changed.
Properties of the medium through which mechanical waves can be propagated :
For the propagation of mechanical waves through a medium, the medium must possess the following properties :
- The medium must be continuous and elastic so that it can regain its original condition as soon as the disturbance passes away.
- The medium should possess inertia so that it is capable of storing energy and transferring it in the form of waves.
- The medium should also have negligible viscosity so that oscillations of the particles are not significantly damped and the wave travels longer distance.
Remember : Electromagnetic waves do not need any material medium for propagation.
(vii) Phase and phase difference:
Phase of waves : The state of oscillation of a particle is called its phase.
In order to describe the phase at a place, we need to know
- the displacement
- the direction of velocity
- the oscillation number (during which oscillation) of the particle there.
Let us consider propagation of a mechanical wave. We shall consider a simple case where the wave travels along the positive x-axis and the displacement (y) of a particle of the medium from its equilibrium position is given by
y(x,t) = a sin\((\frac{2π}{λ}x+2πnt+Φ)\)
Here, a is the amplitude, λ is the wavelength and n is the frequency of wave motion. x denotes the equilibrium position of the particle and t denotes time. Φ is a constant. y may be along the x axis or perpendicular to it.
In this case, the state of oscillation of a particle of the medium is called the phase of the particle and also of the wave. The quantity \((\frac{2π}{λ}x+2πnt+Φ)\) is the phase of the particle at time t.
To describe the phase of a particle at a place, its displacement, direction of velocity and oscillation number are required.

In above Fig. particles P and Q (or E and C or B and D) have same displacements but the directions of the their velocities are opposite. Such particles are said to be out of phase during their respective oscillations.
Particles B and F have same magnitude of displacements and same direction of velocity. Such particles are said to be in phase during their respective oscillations. Also, these are successive particles with this property of having same phase.
Phase difference: Phase difference is, the difference in phases of two particles at a given instant, the difference in phases of the same particle at different instants.
- At the instant the above graph is drawn, the disturbance (energy) has just reached the particle A. At this instant, particle B has completed quarter oscillation and reached its positive maximum.
- The phase angle θ of this particle B is π/2 = 90° at this instant. Similarly, phase angles of particles C and E are π (180°) and 2π (360°) respectively.
- B and F are the successive particles in the same state during their respective oscillations. Separation between these two is wavelength (λ). Phase angle between these two differs by 2π radian.
- Hence wavelength is better understood as the separation between two particles with phase difference of 2π.
Characteristics of a progressive mechanical wave :
- Without the physical transfer of mass, energy is conveyed from particle to particle.
- The particles of the medium oscillate regularly around their equilibrium locations.
- Without dissipative forces, every particle vibrates with the same amplitude and frequency but varies in phase from its adjacent particles.
- Every particle lags behind the one preceding it in its state of motion.
- A wave motion is doubly periodic, that is, it is periodic in both time and space.
Transverse Waves and Longitudinal Waves:
Progressive waves can be of two types, transverse and longitudinal waves.
Transverse waves : A wave in which particles of the medium vibrate in a direction perpendicular to the direction of propagation of wave is called transverse wave.
Examples :
- A rope with one end fixed is held stretched by hand. When the hand is moved up and down rapidly, perpendicular to the length of the rope, transverse vibrations of the parts of the rope travel away as a succession of crests and troughs, Fig. (a).
- If a long metal bar is periodically struck perpendicular to its length [say, by a hammer as in Fig. (b), a bending-type deformation propagates along the bar as shown.

Characteristics of transverse waves.
- All particles of the medium in the path of the wave vibrate in a direction perpendicular to the direction of propagation of the wave with same period and amplitude.
- When transverse wave passes through a medium, the medium is divided into alternate the crests i.e., regions of positive displacements and troughs i.e., regions of negative displacements.
- A crest and an adjacent trough form one cycle of a transverse wave. The distance measured along the wave between any two consecutive points in the same phase (crest or trough) is called the wavelength of the wave.
- Crests and troughs advance in the medium and are responsible for transfer of energy.
- Transverse waves can travel through solids and on surfaces of liquids only. They cannot travel through liquids and gases.
- When transverse waves advance through a medium there is no change in the pressure and density at any point of medium, however shape changes periodically.
- If vibrations of all the particles along the path of a wave are constrained to be in a single plane, then the wave is called polarised wave. Transverse wave can be polarised.
- Medium conveying a transverse wave must possess elasticity of shape.
Longitudinal waves : A wave in which particles of the medium vibrate in a direction parallel to the direction of propagation of wave is called longitudinal wave. Sound waves are longitudinal waves.
Examples :
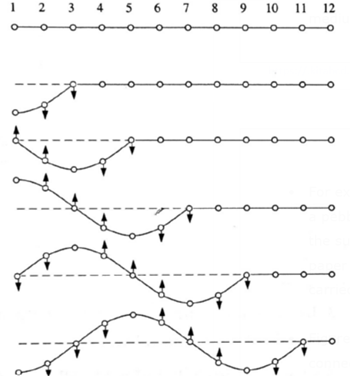
(1) As shown in Fig. (a), a long spring (slinky) is coupled at one end to a basic oscillating mechanism. When the metal ball is pushed slightly to one side and released, its oscillations compress and stretch the spring on a regular basis. As a result, a wave motion propagates along the spring's length. Because each coil of the spring oscillates throughout its length, the wave motion is longitudinal.
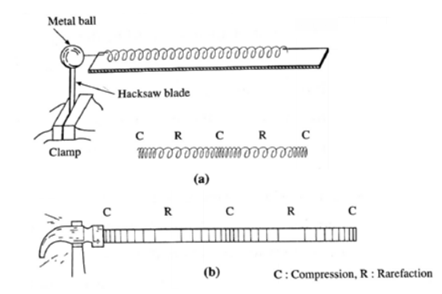
(2) If a long metal bar is periodically struck on one end, above Fig.(b) each impact compresses the material of the bar followed by an expansion. The particles of the bar move back and forth and thus a longitudinal wave travels along the bar.
Characteristics of a longitudinal wave :
- The individual particles of the medium vibrate along the direction of propagation of the wave with the same period and amplitude.
- The progressively changing phase of the successive particles results in the formation of typical alternate regions of compressions and rarefactions that are periodic in space and time. A compression and an adjacent rarefaction form one cycle of a longitudinal wave.
- Periodic compressions and rarefactions result in periodic pressure and density variations in the medium.
- Propagation of a longitudinal wave depends on the ability of the medium to resist change in volume. Hence, the medium must possess the bulk modulus.
- A longitudinal wave can propagate through any material medium i.e., solid, liquid or gas. It cannot travel through vacuum.
- As the direction of vibration of the particles of the medium is along the direction of propagation of the wave, the question of polarization does not arise
Mathematical expression for a transverse progressive wave travelling along the positive x-axis :
Consider a transverse sinusoidal wave travelling in the direction of the positive x—axis.
The displacement of a particle of the medium from its equilibrium position as a function of its position x and time t is given by
y(x, t) = a sin (kx — ωt + Φ) …(1)
where a = amplitude of the wave,
k = angular wave number = \(\frac{2π}{λ}\) being the wavelength of the wave,
ω = angular frequency of the wave = 2πn, n being the frequency of the wave,
Φ = initial phase angle or phase constant, (kx — ωt + Φ) = the argument of the sine function gives the phase of the particle and also the phase of the wave at position x and time t.
The physical quantities a, k, ω, Φ in the above equation are constant.
Explanation/Justification : At a certain instant, say t = t0. Eq. (1) becomes,
y(x, t0) = a sin (kx — ωt0 + Φ) = a sin (kx + constant)
i.e., the shape of the wave as a function of x is a sine wave, at any instant.
On the other hand, at a fixed location, say x = x0, Eq. (1) becomes,
y(x0, t) = a sin (kx0 — ωt + Φ) = a sin (constant — ωt)
Thus, displacement y varies sinusoidally with time, at a fixed location. That is, the particles of the medium at different positions execute simple harmonic motion about their equilibrium positions. For the argument of the sine function (kx — ωt + Φ) to remain constant, x must increase in the positive direction as t increases.
Thus, Eq. (1) represents a wave travelling in the direction of the positive x-axis.
This equation is applicable also to a longitudinal wave.
Transverse progressive wave travelling along the negative x-axis :
A sinusoidal progressive wave travelling in the direction of the negative x-axis is given by y(x, t) = a sin (kx + ωt + Φ),
where y(x, t) = displacement as a function of position x and time t,
The Speed of Travelling Waves :
- Speed of a mechanical wave depends upon the elastic properties and density of the medium.
- The same medium can support both transverse and longitudinal waves which have different speeds.
The speed of transverse waves :
- The speed of a wave is determined by the restoring force produced in the medium when it is disturbed.
- The waves produced on a string are transverse waves. In this case the restoring force is provided by the tension T in the string.
The formula for speed of transverse wave on stretched string is given by
v = \(\sqrt{\frac{T}{m}}\)
The speed of a transverse wave depends only on the properties of the string, T and m. It does not depend on wavelength or frequency of the wave.
The speed of longitudinal waves :
In case of longitudinal waves, the particles of the medium oscillate forward and backward along the direction of wave propagation. This causes compression and rarefaction which travel in the medium as the medium possess elastic property.
Formation of sound waves in air :
Sound is produced by a vibrating body and it propagates through a medium as a longitudinal progressive wave.
Explanation :
Consider how a tuning fork produces sound waves in air as shown in below Fig.
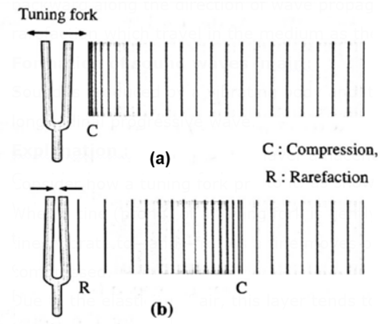
- When a tine (prong) of a tuning fork is gently struck by a rubber hammer, both the tines vibrate to—and—fro.
- As a tine moves outward, the layer of air next to it gets compressed. Due to the elasticity of air, this layer tends to expand back.
- In doing so, it compresses the layer adjacent to it, as shown in Fig. (a). This process continues and a region of compression travels through the air.
- Meanwhile, the tines move inward. This decreases the pressure on the layer next to a tine and creates a region of rarefaction, as shown in Fig. (b).
- When the first layer rushes to occupy this partial vacuum, the region of rarefaction moves outward. This way, the region of rarefaction follows the compression outward.
- Thus, as the tines vibrate, the resulting sound travels as a train of longitudinal compression and rarefaction.
- Vocal cords in our larynx and the reeds of a mouth organ or harmonium also produce sound the same way.
Remember: When a sound wave goes from one medium to another its velocity changes along with its wavelength. Its frequency, which is decided by the source remains constant.
Newton's formula for velocity of sound and its limitation :
Propagation of longitudinal waves was studied by Newton. Newton (in 1687) derived the relation between the speed of sound, and the inertia and the elastic property of the medium :
v = \(\sqrt{\frac{K}{ρ}}\)
where v is the wave speed ‘(speed of sound) and ρ and K are respectively the density and the bulk modulus of the medium.
Assumptions : For a theoretical estimate of the speed of sound in air, Newton assumed that the air obeyed Boyle's law and that the pressure variations caused by the passage of the waves are slow and take place isothermally.
Newton's formula : Newton, therefore, used the isothermal bulk modulus, which, for an ideal gas, is equal to the pressure p of the gas.
So, the expression he deduced for the speed of sound in air is
v = \(\sqrt{\frac{K_{isothermal}}{ρ}}\) = \(\sqrt{\frac{p}{ρ}}\)
This is Newton's formula for the speed of sound in an ideal gas.
At NTP, p =1.013 x 105 Pa and
ρair = 1.293 kg/m3, so that
v = \(\sqrt{\frac{1.013×10^5\,Pa}{1.293\,kg/m^3}}\) = 280 m/s
Limitation : At NTP, the value of speed of sound given by Newton's formula (280 m/s) is significantly less (by about 16%) than the experimental value of 331.3 m/s.
Newton could not give satisfactory explanation of this discrepancy.
- Specific heat of a gas at constant pressure : The quantity of heat required to change the temperature of a unit mass of gas through 1 K when pressure is kept constant is called the specific heat of the gas at constant pressure (CP).
- Specific heat of a gas at constant volume : The quantity of heat required to change the temperature of a unit mass of gas through 1 K when volume is kept constant is called the specific heat of the gas at constant volume (CV).
Laplace’s correction :
- Newton thought that pressure fluctuations produced by wave passage occurred isothermally when calculating the speed of sound in air. As a result, he applied the isothermal bulk modulus to air. However, his estimate of around 280 m/s at NTP is much lower than the actual measurement of 331.3 m/s under the same circumstances.
- In 1817, Pierre Simon Laplace observed that because gases are poor heat conductors and pressure fluctuations are rapid there is little time for the heat produced to be transmitted away from the affected sections of the gas. This implies that compressions and rarefactions occur adiabatically. As a result, the adiabatic bulk modulus is the proper modulus of elasticity.
For an ideal gas, the adiabatic bulk modulus K(adiabatic) = νp
where p is the pressure of the gas and ν is the ratio of the specific heat of the gas at constant pressure to that at constant volume. ν is called the adiabatic ratio or adiabatic constant.
The expression for the speed of sound in air (or gas, in general) now becomes
v = \(\sqrt{\frac{γp}{ρ}}\)
which is called Laplace’s formula.
The value of ν for air is 1.403. Multiplying Newton's estimated value 279.9 m/s by
= 1.184, we have v = 331.4 m/s, in very close agreement with the experimental value 331.3 m/s.
Factors affecting speed of sound:
As sound waves travel through atmosphere (open air), some factors related to air affect the speed of sound.
(i) Effect of pressure on the velocity (speed) of sound :
According to Laplace's formula, the speed of sound in a gas is
v = \(\sqrt{\frac{γp}{ρ}}\) …..(1)
where p and ρ are the pressure and density of the gas and
ν = CP/CV
In terms of the density of the gas, the equation of state for an ideal gas is written as
\(\frac{p}{ρT}=\frac{R}{M}\) = constant ….(2)
where T is the absolute temperature, R is the universal gas constant and M is the molar mass.
Therefore, at constant T,
\(\frac{p}{ρ}\) = constant …..(3)
Hence, v = \(\sqrt{\frac{γp}{ρ}}\) = constant ……(4)
Thus, at constant temperature, the speed of sound in a gas is independent of the pressure provided the pressure is atmospheric or below, so that the gas closely approximates an ideal gas.
(ii) Effect of temperature on the speed of sound in a gas :
The equation of state for an ideal gas is
pv = nRT= \(\frac{m}{M}\) RT
where m is the mass of n moles of the gas,
M = m/n is the molar mass, T is the absolute temperature and R is the universal gas constant.
Since ρ = m/V where V is the volume of the gas,
\(\frac{p}{ρ}\) = \(\frac{pV}{m}\) = \(\frac{RT}{M}\)…..(2)
∴ v = \(\sqrt{\frac{γp}{ρ}}\) = \(\sqrt{\frac{γRT}{M}}\)
For a fixed mass of given gas, ν and M are constants.
∴ v ∝ \(\sqrt{T}\) ….(3)
This shows that the speed of sound in a gas is directly proportional to the square root of its absolute temperature.
Increase in the speed of sound in a gas for 1 °C rise in temperature :
Let v0 be the speed of sound in a gas at temperature T0K = 0 °C and v be the speed of sound in the gas at temperature T K = 1 °C.
Using Laplace's formula and ideal gas equation,
v0 = \(\sqrt{\frac{γ\,nRT_0}{M}}\) ….(1)
v = \(\sqrt{\frac{γ\,nRT}{M}}\) ….(2)
where ν = CP/CV, n is the number of moles, R is the universal gas constant and M is the mass of gas.
From Eqs. (1) and (2), we have,
\(\frac{v}{v_0}=\sqrt{\frac{T}{T_0}}\)
Now, T0 = 0 °C = 273K and T = 1°C = 274K
∴ \(\frac{v}{v_0}=\sqrt{\frac{274}{273}}\) = \(\sqrt{1+\frac{1}{273}}\)
∴ v = \(v_0(1+\frac{1}{273})^{1/2}\) ≈ = \(v_0+(\frac{v_0}{546})\)
(ignoring the higher order terms in the binomial expansion)
At 0 °C, v0 = 331.3 m/s,
∴ v = 331.3 + \(\frac{331.3}{546}\)
= 331.3 + 0.6068 ≈ (331.3 + 0.61) m/s
Thus, for 1 °C rise in temperature, the speed of sound in a gas increases by about 0.61 m/s.
(iii) Effect of humidity of air on the velocity (speed) of sound :
The term humidity is used to express the moisture content in the air. The presence of water vapour in the air affects the density of air which in turn affects the speed of sound in air.
Let vm be the speed of sound in moist air having density ρm and vd the speed of sound in dry air having density ρd.
According to Laplace's formula, vm = \(\sqrt{\frac{γp}{ρ_m}}\) and vd = \(\sqrt{\frac{γp}{ρ_d}}\)
where p is the pressure of air and ν = CP/CV
∴ At constant pressure, \(\frac{v_m}{v_d}=\sqrt{\frac{ρ_d}{ρ_m}}\)
The density of moist air is less than that of dry air.
vm > vd
That is, the speed of sound in moist air is greater than that in dry air.
Principle of Superposition of Waves:
Principle of superposition of waves : When two or more waves arrive at the same time at a point, the resultant displacement at that point, at that instant, is the vector sum of the displacements due to each wave acting independently.
Explanation :
Consider two waves travelling in a medium arriving simultaneously at a point P.
Let y1 and y2 be the displacements due to the two waves at the point. Then, according to the principle of superposition of waves, the resultant displacement at the point is \(\vec{y_R}=\vec{y_1}+\vec{y_2}\)
This implies that, depending upon the phase difference between the two waves,
yR (maximum) = |y1| + |y2 | and
yR (minimum) = |y1| — |y2 |
For same amplitude and frequency :
Consider two waves of the same amplitude and frequency, but opposite in phase, arriving simultaneously at a point. The crest due to one wave coincides with the trough due to the other and vice versa. Therefore, the resultant displacement
\(\vec{y_R}=\vec{y_1}+\vec{y_2}\) = \(\vec{y_R}=\vec{y_1}-\vec{y_1}\) = 0 Thus, the resultant displacement at that point is zero.
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 7: Thermal Properties of Matter – Online Notes
Next Chapter : Chapter 9: Optics – Online Notes
We reply to valid query.