Current Electricity
Maharashtra Board-Class-12th-Physics-Chapter-9
Solutions
Question 1.
Choose the correct option.
(i) Kirchhoff’s first law, i.e., Σ I = 0 at a junction, deals with the conservation of
(A) charge
(B) energy
(C) momentum
(D) mass
(A) charge
(ii) When the balance point is obtained in the potentiometer, a current is drawn from
(A) both the cells and auxiliary battery
(B) cell only
(C) auxiliary battery only
(D) neither cell nor auxiliary battery
(D) neither cell nor auxiliary battery
(iii) In the following circuit diagram, an infinite series of resistances is shown. Equivalent resistance between points A and B is

(A) infinite
(B) zero
(C) 2 Ω
(D) 1.5 Ω
(C) 2 Ω
(iv) Four resistances 10 Ω, 10 Ω, 10 Ω and 15 Ω form a Wheatstone’s network. What shunt is required across 15 Ω resistor to balance the bridge
(A) 10 Ω
(B) 15 Ω
(C) 20 Ω
(D) 30 Ω
(D) 30 Ω
(v) A circular loop has a resistance of 40 Ω. Two points P and Q of the loop, which are one quarter of the circumference apart are connected to a 24 V battery, having an internal resistance of 0.5 Ω. What is the current flowing through the battery.
(A) 0.5 A
(B) 1A
(C) 2A
(D) 3A
(D) 3A
(vi) To find the resistance of a gold bangle, two diametrically opposite points of the bangle are connected to the two terminals of the left gap of a metre bridge. A resistance of 4 Ω is introduced in the right gap. What is the resistance of the bangle if the null point is at 20 cm from the left end?
(A) 2 Ω
(B) 4 Ω
(C) 8 Ω
(D) 16 Ω
(A) 2 Ω
Question 2.
Answer in brief.
(i) Define or describe a Potentiometer.
The potentiometer is a device used for accurate measurement of potential difference as well as the emf of a cell.
- It does not draw any current from the circuit at the null point. Thus, it acts as an ideal voltmeter and it can be used to determine the internal resistance of a cell.
- It consist of a long uniform wire AB of length L, stretched on a wooden board. A cell of stable emf (E), with a plug key K in series, is connected across AB as shown in the following figure.

(ii) Define Potential Gradient.
Potential gradient is defined as the potential difference (the fall of potential from the high potential end) per unit length of the wire.
(iii) Why should not the jockey be slided along the potentiometer wire?
Sliding the jockey on the potentiometer wire decreases the cross sectional area of the wire and thereby affects the fall of potential along the wire.
This affects the potentiometer readings. Hence, the jockey should not be slided along the potentiometer wire.
(iv) Are Kirchhoff’s laws applicable for both AC and DC currents?
Kirchhoff’s laws are applicable to both AC and DC circuits (networks). For AC circuits with different loads, (e.g. a combination of a resistor and a capacitor, the instantaneous values for current and voltage are considered for addition.
(v) In a Wheatstone’s meter-bridge experiment, the null point is obtained in middle one third portion of wire. Why is it recommended?
The value of unknown resistance X, may not be accurate due to non-uniformity of the bridge wire and development of contact resistance at the ends of the wire.
To minimize these errors, the value of R is so adjusted that the null point is obtained in the middle one-third of the wire (between 34 cm and 66 cm) so that the percentage errors in the measurement of lX and lR are minimum and nearly the same.
(vi) State any two sources of errors in meter bridge experiment. Explain how they can be minimized.
Errors are almost unavoidable but can be minimized considerably as follows :
(1) The value of unknown resistance X, may not be accurate due to non-uniformity of the bridge wire and development of contact resistance at the ends of the wire.
To minimize the errors
- The value of R is so adjusted that the null point is obtained to middle one third of the wire (between 34 cm and 66 cm) so that percentage error in the measurement of lX and lR are minimum and nearly the same.
(2) The ends of the wire are soldered to the metallic strip where contact resistance is developed, which is not taken into account.
To minimize the errors
- The experiment is repeated by interchanging the positions of unknown resistance X and known resistance box R.
(vii) What is potential gradient? How is it measured? Explain.
Potential gradient : Potential gradient is defined as the potential difference (the fall of potential from the high potential end) per unit length of the wire.
Consider A potentiometer consists of a long wire AB of length L and resistance R having uniform cross sectional area A. (see above Fig.) A cell of emf E having internal resistance r is connected across AB as shown in the Fig. When the circuit is switched on, current I passes through the wire.

Current through AB, I = \(\frac{E}{R+r}\)
Potential difference across AB. VAB = IR
∴ VAB = \(\frac{ER}{R+r}\)
The potential difference (the fall of potential from the high potential end) per unit length of the wire,
\(\frac{V_{AB}}{L}=\frac{ER}{R+r}\)
As long as E and r remain constant, \(\frac{V_{AB}}{L}\) will remain constant.
\(\frac{V_{AB}}{L}\) is known as potential gradient along AB and is denoted by K.
Thus the potential gradient is calculated by measuring the potential difference between ends of the potentiometer wire and dividing it by the length of the wire.
Let C be any point on the wire between A and B and AC = l = length of the wire between A and C.
Then VAC = Kl
VAC ∝ l as K is constant in a particular case.
Thus, the potential difference across any length of the potentiometer wire is directly proportional to that length. This is the principle of the potentiometer.
(viii) On what factors does the potential gradient of the wire depend?
The potential gradient depends upon the potential difference between the ends of the wire and the length of the wire.
(ix) Why is potentiometer preferred over a voltmeter for measuring emf?
- A voltmeter should ideally have an infinite resistance so that it does not draw any current from the circuit. However a voltmeter cannot be designed to have infinite resistance.
- A potentiometer does not draw any current from the circuit at the null point. Therefore, it gives more accurate measurement. Thus, it acts as an ideal voltmeter.
(x) State the uses of a potentiometer.
. Some practical applications of potentiometer are given below.
- Voltage divider : The potentiometer can be used as a voltage divider to change the output voltage of a voltage supply.
- Audio control : Sliding potentiometers are commonly used in modern low-power audio systems as audio control devices. Both sliding (faders) and rotary potentiometers (knobs) are regularly used for frequency attenuation, loudness control and for controlling different characteristics of audio signals.
- Potentiometer as a sensor : If the slider of a potentiometer is connected to the moving part of a machine, it can work as a motion sensor. A small displacement of the moving part causes changes in potential which is further amplified using an amplifier circuit. The potential difference is calibrated in terms of the displacement of the moving part.
- To measure the emf (for this, the emf of the standard cell and potential gradient must be known).
- To compare the emf’s of two cells.
- To determine the internal resistance of a cell.
(xi) What are the disadvantages of a potentiometer?
Disadvantages of a potentiometer :
- The use of a potentiometer is an indirect measurement method while a voltmeter is a direct reading instrument.
- A potentiometer is unwieldy while a voltmeter is portable.
- Unlike a voltmeter, the use of a potentiometer in measuring an unknown emf requires a standard source of emf and calibration.
(xii) Distinguish between a potentiometer and a voltmeter.
| Potentiometer | Voltmeter |
| A potentiometer is used to determine the emf of a cell, potential difference and internal resistance. | A voltmeter can be used to measure the potential difference and terminal voltage of a cell. But it cannot be used to measure the emf of a cell. |
| Its accuracy and sensitivity are very high. | Its accuracy and sensitivity are less as compared to a potentiometer. |
| It is not a portable instrument. | It is a portable instrument. |
| It does not give a direct reading. | It gives a direct reading. |
(xiii) What will be the effect on the position of zero deflection if only the current flowing through the potentiometer wire is (i) increased (ii) decreased.
(i) On increasing the current through the potentiometer wire, the potential gradient along the wire will increase. Hence, the position of zero deflection will occur at a shorter length.
(ii) On decreasing the current through the potentiometer wire, the potential gradient along the wire will decrease. Hence, the position of zero deflection will occur at a longer length.
(3) Obtain the balancing condition in case of a Wheatstone’s network.
Wheatstone’s network and condition of balance :
Wheatstone’s network or bridge is a circuit for indirect measurement of resistance by null comparison method by comparing it with a standard known resistance.

It consists of four resistors with resistances P, Q, R and S arranged in the form of a quadrilateral ABCD.
A cell (E) with a plug key (K) in series is connected across one diagonal AC and a galvanometer (G) across the other diagonal BD as shown in the following figure.
With the key K closed, currents pass through the resistors and the galvanometer. One or more of the resistances is adjusted until no deflection in the galvanometer can be detected. The bridge is then said to be balanced.
Let I be the current drawn from the cell. At junction A, it divides into a current I1 through P and a current I2 through S.
I = I1 + I2 (by Kirchhoff’s first law).
At junction B, current Ig flows through the galvanometer and current I1 − Ig flows through Q.
At junction D, I2 and Ig combine. Hence, current I2 + Ig flows through R from D to C. At junction C, I1 − Ig and I2 + Ig combine.
Hence, current I1 + I2(=I) leaves junction C.
Applying Kirchhoff’s voltage law to loop ABDA in a clockwise sense, we get,
−I1P − IgG + I2S = 0 …….(1)
where G is the resistance of the galvanometer.
Applying Kirchhoff’s voltage law to loop BCDB in a clockwise sense, we get,
− (I1 − Ig)Q + (I2 + Ig)R + IgG = 0 …….(2)
When Ig = 0, the bridge (network) is said to be balanced.
In that case, from Eqs. (1) and (2), we get,
I1P = I2S ……(3)
and I1Q = I2R ……(4)
From Eqs. (3) and (4), we get,
P/Q = S/R
This is the condition of balance.
(4) Explain with neat circuit diagram, how you will determine the unknown resistance by using a meter-bridge.
A metre bridge consists of a rectangular wooden board with two L-shaped thick metallic strips fixed along its three edges. A single thick metallic strip separates two L-shaped strips. A wire of length one metre and uniform cross section is stretched on a metre scale fixed on the wooden board. The ends of the wire are fixed to the L-shaped metallic strips.

Determining unknown resistance using meter bridge :
An unknown resistance X is connected in the left gap and a resistance box R is connected in the right gap as shown in Fig. One end of a centre-zero galvanometer (G) is connected to terminal C and the other end is connected to a pencil jockey (J).
A cell (E) of emf E, plug key (K) and rheostat (Rh) are connected in series between points A and B.
Working : Keeping a suitable resistance (R) in the resistance box, key K is closed to pass a current through the circuit. The jockey is tapped along the wire to locate the equipotential point D when the galvanometer shows zero deflection. The bridge is then balanced and point D is called the null point and the method is called as null deflection method.
The distances IX and IR of the null point from the two ends of the wire are measured.
According to the principle of Wheatstone’s network,
\(\frac{X}{R}=\frac{\text{resistance of the wire of length}I_X(R_{AD})}{\text{resistance of the wire of length}I_R(R_{DB})}\)
∴ \(\frac{X}{R}=\frac{R_{AD}}{R_{DB}}\)
Now, R = where l is the length of the wire, ρ is the resistivity of the material of the wire and A is the area of cross section of the wire.
∴ RAD = \(ρ\frac{l_X}{A}\) and RDB = \(ρ\frac{l_R}{A}\)
∴ \(\frac{X}{R}=\frac{R_{AD}}{R_{DB}}\) =\(\frac{ρl_X/A}{ρl_R/A}=\frac{l_X}{l_R}\)
∴ X = \(\frac{l_X}{l_R}\)xR
As R, lX and lR are known, the unknown resistance X can be calculated.
(5) Describe Kelvin’s method to determine the resistance of a galvanometer by using a meter bridge.
Kelvin’s method :
Circuit :The metre bridge circuit for Kelvin’s method of determination of the resistance of a galvanometer is shown in below Fig. The gaivanometer whose resistance G is to be determined, is connected in one gap of the metre bridge-
A resistance box providing a variable known resistance R is connected in the other gap. The junction B of the galvanometer and the resistance box is connected directly to a pencil jockey. A cell of emf E, a key (K) and a rheostat (Rh) are connected across AC.

Working :
Keeping a suitable resistance R in the resistance box and maximum resistance in the rheostat, key K is closed to pass the current.
The rheostat resistance is slowly reduced such that the galvanometer shows about 2/3rd of the full—scale deflection.
On tapping the jockey at end-points A and C, the galvanometer deflection should change to opposite sides of the initial deflection. Only then will there be a point D on the wire which is equipotential with point B.
The jockey is tapped along the wire to locate the equipotential point D when the galvanometer shows no change in deflection.
Point D is now called the balance point and Kelvin's method is thus an equal deflection method. At this balanced condition,
\(\frac{G}{R}\)=\(\frac{\text{resistance of the wire of length}I_G}{\text{resistance of the wire of length}I_R}\)
where IG ≡ the length of the wire opposite to the galvanometer,
IR ≡ the length of the wire opposite to the resistance box.
If λ ≡ the resistance per unit length of the wire,
\(\frac{G}{R}\)=\(\frac{λI_G}{λI_R}\)=\(\frac{I_G}{I_R}\)
∴ G = R\(\frac{I_G}{I_R}\)
The quantities on the right hand side are known, so that G can be calculated.
(6) Describe how a potentiometer is used to compare the emfs of two cells by connecting the cells individually.
A battery of stable emf E is used to set up a potential gradient V/L along a potentiometer wire, where V ≡ potential difference across the length L of the wire. The positive terminals of the cells, whose emf’s (E1 and E2) are to be compared, are connected to the high potential terminal A. The negative terminals of the cells are connected to a galvanometer G through a two-way key. The other terminal of the galvanometer is connected to a pencil jockey. The emf E should be greater than both the emf’s E1 and E2.

Connecting point P to C, the cell with emf E1 is brought into the circuit. The jockey is tapped along the wire to locate the null point D at a distance l1 from A. Then,
E1 = l1(V/ L)
Now, without changing the potential gradient (i.e., without changing the rheostat setting) point Q (instead of P) is connected to C, bringing the cell with emf E2 into the circuit. Let its null point D’ be at a distance l2 from A, so that
E2 = l2(V/ L)
∴ E1/E2 = l1/l2
Hence, by measuring the corresponding null lengths l1 and l2, E1/E2 can be calculated. The experiment is repeated for different potential gradients using the rheostat.
(7) Describe how a potentiometer is used to compare the emfs of two cells by combination method.
A battery of stable emf E is used to set up a potential gradient V/L, along the potentiometer wire, where V ≡ potential difference across length L of the wire.
The positive terminal of the cell 1 is connected to the higher potential terminal A of the potentiometer; the negative terminal is connected to the galvanometer G through the reversing key. The other terminal of the galvanometer is connected to a pencil jockey.
The cell 2 is connected across the remaining two opposite terminals of the reversing key. The other terminal of the galvanometer is connected to a pencil jockey.
The emf E1 should be greater than the emf E2; this can be adjusted by trial and error.

Two plugs are inserted in the reversing key in positions 1—1. Here, the two cells assist each other so that the net emf is E1 + E2. The jockey is tapped along the wire to locate the null point D. If the null point is a distance l1 from A,
E1 + E2 = l1 (V/L)
For the same potential gradient (without changing the rheostat setting), the plugs are now inserted into position 2—2. (instead of 1—1).
The emf E2 then opposes E1 and the net emf is E1 − E2.
The new null point D’ is, say, a distance l2 from A and
E1 − E2 = l2 (V/L)
∴ \(\frac{E_1+E_2}{E_1-E_2}=\frac{l_1}{l_2}\)
∴ \(\frac{E_1}{E_2}=\frac{l_1+l_2}{l_1-l_2}\)
Here, the emf E should be greater than E1 + E2
The experiment is repeated for different potential gradients using the rheostat.
(8) Describe with the help of a neat circuit diagram how you will determine the internal resistance of a cell by using a potentiometer. Derive the necessary formula.
Principle : A cell of emf E and internal resistance r, which is connected to an external resistance R, has its terminal potential difference V less than its emf E.
If I is the corresponding current,
\(\frac{E}{V}=\frac{I(R+r)}{IR}\)=\(\frac{R+r}{R}\)
= \(1+\frac{r}{R}\) ( when R → ∞, v→ E)
∴ r = \(\frac{E-V}{V}R\)
Working : A battery of stable emf E’ is used to set up a potential gradient V/L, along the potentiometer wire, where V ≡ potential difference across the length L of the wire.

The negative terminal is connected through a centre-zero galvanometer G to a pencil jockey. A resistance box R with a plug key K in series is connected across the cell.
Firstly, key K is kept open; then, effectively, R = ∞. The jockey is tapped on the potentiometer wire to locate the null point D. Let the null length
AD = l1, so that
E = (VAB/L)l1
With the same potential gradient, and a small resistance R in the resistance box, ‘key K is closed.
The new null length AD’ = l2 for the terminal potential difference V is found :
V = (VAB /L)l2
∴ E/V = \(\frac{l_1}{l_2}\) ∴\(\frac{E-V}{V}\)=\(\frac{l_1-l_2}{l_2}\)=\(\frac{l_1}{l_2}-1\)
Now r = \(\frac{E-V}{V}R\)
∴ r = \(R(\frac{l_1}{l_2}-1)\)
R, l1 and l2 being known, r can be calculated. The experiment is repeated with different potential gradients using the rheostat or with different values of R.
(9) On what factors does the internal resistance of a cell depend?
The internal resistance of a cell depends on :
- Nature of the electrolyte : The greater the conductivity of the electrolyte, the lower is the internal resistance of the cell.
- Separation between the electrodes : The larger the separation between the electrodes of the cell, the higher is the internal resistance of the cell. This is because the ions have to cover a greater distance before reaching an electrode.
- Nature of the electrodes.
- The internal resistance is inversely proportional to the common area of the electrodes dipping in the electrolyte.
(10) A battery of emf 4 volt and internal resistance 1 Ω is connected in parallel with another battery of emf 1 V and internal resistance 1 Ω (with their like poles connected together). The combination is used to send current through an external resistance of 2 Ω. Calculate the current through the external resistance.
Let I1 and I2 be the currents through the two branches as shown in Fig.
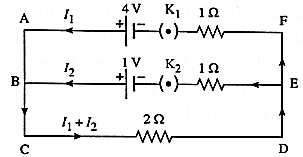
The current through the 2 Ω resistance will be (I1 + I2) [Kirchhoff's current law].
Applying Kirchhoff’s voltage law to loop ABCDEFA, we get,
−2(I1 + I2) − 1(I1) + 4 = 0
3I1 + 2I2 = 4 ….(1)
Applying Kirchh0ff’s voltage law to loop BCDEB we get,
−2(I1 + I2) − 1(I2) + 1 = 0
2I1 + 3I2 = 1 …..(2)
Multiplying Eq. (1) by 2 and Eq. (2) by 3, we get,
6I1 + 4I2 = 8 ……(3)
and 6I1 + 9I2 = 3 ……(4)
Subtracting Eq. (4) from Eq. (3), we get,
−5I2 = 5
∴ I2 = −1A
The minus sign shows that the direction of current I2 is opposite to that assumed. Substituting this value of I2 in Eq. (1), we get,
3I1 + 2(−1) = 4
∴ 3 I1 = 4 + 2 = 6
∴ I1 = 2A
Current through the 2 Ω resistance = I1 + I2 = 2 – 1 = 1A It is in the direction as shown in figure.
(11) Two cells of emf 1.5 Volt and 2 Volt having respective internal resistances of 1 Ω and 2 Ω are connected in parallel so as to send current in same direction through an external resistance of 5 Ω. Find the current through the external resistance.
Let I1 and I2 be the currents through the two branches as shown in Fig.

The current through the 5 Ω resistor will be I1 + I2 [Kirchhoff’s current law].
Applying Kirchhoff’s voltage law to loop ABCDEFA, we get,
−5(I1 + I2) − I1 + 1.5 = 0
6I1 + 5I2 = 1.5 ….(1)
Applying Kirchh0ff’s voltage law to loop BCDEB we get,
−5(I1 + I2) − 2I2 + 2 = 0
5I1 +7I2 = 2 ….(2)
Multiplying Eq. (1) by 5 and Eq. (2) by 6, we
30I1 + 25I2 = 7.5
and 30I1 + 42I2 = 12
Subtracting Eq. (3) from Eq. (4), we get,
17I2 = 4.5
∴ I2 = 4.5/17 A
Substituting this value of I2 in Eq. (1), we get,
6I1 + 5(4.5/17) = 1.5 (3)
∴ 6I1 + (22.5/17) = 1.5
∴ 6I1 = \(1.5-\frac{22.5}{17} = \frac{28.5-22.5}{17}\)
= \(\frac{3}{17}\)
∴ I1 = \(\frac{3}{17×6}\) = \(\frac{0.5}{17}\)A
Current through the 5 Ω resistance (external resistance)
= I1 + I2 = \(\frac{0.5}{17}+\frac{4.5}{17}\) = \(\frac{5}{17}\)A
(12) A voltmeter has a resistance 30 Ω. What will be its reading, when it is connected across a cell of emf 2 V having internal resistance 10 Ω?
Given : E =2V, r = 10 Ω , R =30 Ω
The voltmeter reading,
V = IR = \((\frac{E}{R+r})R\)
= \((\frac{2}{30+10})30\)
= \(\frac{3}{2}\) = 1.5 V
(13) A set of three coils having resistances 10 Ω, 12 Ω and 15 Ω are connected in parallel. This combination is connected in series with series combination of three coils of the same resistances. Calculate the total resistance and current through the circuit, if a battery of emf 4.1 Volt is used for drawing current.
Figure shows the electrical network. For resistances 10 Ω, 12 Ω and 15 Ω connected in parallel the equivalent resistance (Rp) is given by,
\(\frac{1}{R_p}\)=\(\frac{1}{10}+\frac{1}{12}+\frac{1}{15}\) = \(\frac{6+5+4}{60}=\frac{1}{4}\)
∴ Rp = 4

For resistance RP, 10 Ω, 12 Ω and 15 Ω connected in series, the equivalent resistance,
Rs = 4 + 10 + 12 + 15 = 41 Ω
Thus, the total resistance = Rs = 41 Ω
Now, V = IRs
4.1 = I x 41
∴ I = 0.1 A
The total resistance and current through the circuit are 41 Ω and 0.1 A respectively.
(14) A potentiometer wire has a length of 1.5 m and resistance of 10 Ω. It is connected in series with the cell of emf 4 Volt and internal resistance 5 Ω. Calculate the potential drop per centimeter of the wire.
Given : L = 1.5 m, R = 10 Ω, E = 4V, r = 5 Ω.
K = \(\frac{ER}{(R+r)L}\)
∴ K = \(\frac{4×10}{(10+5)1.5}=\frac{40}{22.5}\frac{V}{m}=\frac{40}{2250}\frac{V}{cm}\) = 0.0178 V/cm
The potential drop per centimeter of the wire is 0.0178 V/cm
(15) When two cells of emfs. E1 and E2 are connected in series so as to assist each other, their balancing length on a potentiometer is found to be 2.7 m. When the cells are connected in series so as to oppose each other, the balancing length is found to be 0.3 m. Compare the emfs of the two cells.
Given : l1 = 2.7 m (cells assisting), l2 = 0.3 m (cells opposing)
E1 + E2 = Kl1 and E1 − E2 = Kl2
∴ \(\frac{E_1+E_2}{E_1-E_2}=\frac{Kl_1}{Kl_2}\)
∴ \(\frac{E_1}{E_2}=\frac{l_1+l_2}{l_1-l_2}=\frac{2.7+0.3}{2.7-0.3}=\frac{3}{2.4}\)= 1.25
The ratio of the emf's of the two cells is 1.25
(16) The emf of a cell is balanced by a length of 120 cm of potentiometer wire. When the cell is shunted by a resistance of 10 Ω, the balancing length is reduced by 20 cm. Find the internal resistance of the cell.
Given : R = 10 Ω, l1 =120 cm, l2 = 120—20 = 100 cm
r = R\((\frac{l_1-l_2}{l_2})\) = \(10(\frac{120-100}{100})\)
= 2 Ω
The internal resistance of the cell is 2 Ω.
(17) A potential drop per unit length along a wire is 5 x 10-3 V/m. If the emf of a cell balances against length 216 cm of this potentiometer wire, find the emf of the cell.
Given : K = 5 x 10−3 V/m, L = 216 cm = 216 x 10−2 m
E = KL
∴ E = 5 x 10−3 x 216 x 10−2
= 1080 x 10−5
= 0.01080 V
The emf of the cell is 0.01080 volt.
(18) The resistance of a potentiometer wire is 8 Ω and its length is 8 m. A resistance box and a 2 V battery are connected in series with it. What should be the resistance in the box, if it is desired to have a potential drop of 1μV/mm?
Given : R = 8 Ω, L = 8m, E = 2V, K = 1 μV/mm = 1 x 10−3 V/m
K = V/L = \(\frac{ER}{(R+R_B)L}\), where RB is the resistance in the box.
∴ 1 x 10−3 = \(\frac{2×8}{(8+R_B)8}\)
∴ 8 + RB = 2/10−3 = 2 x 103
∴ RB = 2000 − 8
= 1992 Ω
(19) Find the equivalent resistance between the terminals of A and B in the network shown in the figure below given that the resistance of each resistor is 10 ohm.

Applying Kirchhoff’s voltage law to loop FGHF, we get,
−10I1 − 10(I1 − I2) + 10(I − I1) + 10(I − I1) =0
−10I1 − 10I1 + 10I2 + 10I − 10I1 + 10I – 10I1 = 0
20I − 40I1 + 10I2 = 0
2I – 4I1 + I2 = 0 …….(1)
Applying Kirchhoffs voltage law to loop GABHG, we get,
−10I2 − 10I2 + 10(I − I2)+ 10(I1 − I2) = 0
– 20I2 + 10I – 10 I2 + 10I1 – 10I2 = 0
10I + 10I1 – 40I2 = 0
I + I1 – 4I2 = 0 ……(2)
Applying Kirchhoff’s voltage law to loop EFHBCDE, we get,
–10(I − I1) − 10(I − I1) − 10(I − I2) + E =0
− 10I + 10 I1 − 10I+ 10 I1 − 10I+ 10 I2 + E =0
E = 30I – 20I1 − 10I2 …..(3)
From Eq. (1), we get, I2 = 4I1 – 2I …..(4)
From Eqs. (2) and (4), we get,
I + I1 − 4(4I1 − 2I) = 0
I + I1 – 16I1 + 8I = 0
I + I1 − 4(4I1 – 2I) = 0
I + I1 – 16I1 + 8I = 0
9I = 15I1 ∴ I1 = \(\frac{9}{15}I = \frac{3}{5}I\) …..(5)
From Eqs. (4) and (5), we get,
I2 = 4\((\frac{3}{5}I)\) − 2I = \(\frac{12}{5}I\) − 2I
= \(\frac{12I-10I}{5}\) = \(\frac{2}{5}I\) …..(6)
From Eqs. (3), (5) and (6), we get
E = 30I − 20\((\frac{3}{5}I)\) − 10\((\frac{2}{5}I)\) = 30I − 12I – 4I
∴ E = 14 I
If R is the equivalent resistance between E and C,
E = RI
∴ R = 14 Ω
(20) A voltmeter has a resistance of 100 Ω. What will be its reading when it is connected across a cell of emf 2 V and internal resistance 20 Ω?
Given : E = 2V, r = 20 Ω , R = 100 Ω
The voltmeter reading,
V = IR = \((\frac{E}{R+r})R\)
= \((\frac{2}{100+20})100=\frac{200}{120}\) = 1.667 V
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-8-Electrostatics –Online Solutions Next Chapter : Chapter-10-Magnetic Fields due to Electric Current – Online Solutions
We reply to valid query.