Sets
Class-9-Mathematics-1-Chapter-1-Maharashtra Board
Notes
|
Topics to be learn : Part -1
|
Sets :
When we can definitively and clearly determine the objects of a given collection, we call that collection a set.
- Therefore, “A set is a well-defined collection of objects”
- Capital English letters A, B, C, etc. are used to denote a set.
- The individual object of the set is known as the member or an element of the set.
- The elements of the set are denoted by lower case letters a, b, c, etc.
- If ‘a’ is an element of set A, then it is written as a ∈ A, and is read as ‘a is an element of set A’ or ‘a is a member of set A’.
- If a is not an element of set A, then it is written as a ∉ The symbol ∉ stands for ‘is not an element of’ or ‘is not a member of’.
Examples of set of numbers :
- Set of natural numbers : N = { 1, 2, 3, . . .}
- Set of whole numbers : W = {0, 1, 2, 3, . . .}
- Set of integers : I = {..., -3, -2, -1, 0, 1, 2, ...}
- Q is a set of rational numbers.
- R is a set of real numbers.
Methods of writing sets
There are two methods of writing set.
(1) Listing method or roster method :
- In this method, all the elements of a set in curly bracket.
- Each of the elements is written only once and separated by commas.
- The order of an element is not important but it is necessary to write all the elements of the set.
e.g. the set of odd numbers between 1 and 10,
A = {3, 5, 7, 9} or A = {7, 3, 5, 9}
- If an element comes more than once, i.e. an element even if repeated, is listed only once.
e.g. the set of the digits in the number 237213,
A = {2,3,7,1} or A = {1,2,3,7}. ,
e.g. set of letters of ‘remember’ word
A = {r, e, m, b}
(2) Rule Method or Set Builder Form :
In this method, the elements are not listed. The elements of the set are described by specifying the property which determines the elements of the set uniquely.
e.g. the set of odd numbers from 1 to 10 is written as follows :
- Listing method : A = {1, 3, 5, 7, 9}.
- Rule method 1 A = {x| x is an odd number less than 10}.
The vertical line ( | ) stands for such that
Examples :
(i) The set of all ‘x’ such that ‘x’ is a natural number between 1 and 10'.
- A = {x | x ∈ N, 1 < x < 10 }
(ii) Set B contains all the prime numbers between 1 and 10
- Listing method : B = {2, 3, 5, 7}
- Rule method : B = { x | x is a prime number between 1 and 10}
(iii) Q is the set of rational numbers
- Set builder form : Q ={ | p, q ∈ I, q ≠ 0} read as ‘Q’ is set of all numbers in the form such that p and q are integers where q is a non-zero number.’
| Listing or Roster Method | Rule Method |
| A = { 2, 4, 6, 8, 10, 12, 14} | A = {x | x is an even natural number less than 15} |
| B: {4, 9, 16} | B = { x | x is a perfect square number between 1 to 20} |
| C = { a, e, i, o, u} | C = {y | y is a vowel in English alphabet} |
| D = {V, I, B, G, Y, O, R} | D = { y | y is a colour in the rainbow} |
| P = {−2, −1, 0, 1, 2} | P = {x | x is an integer and , −3 < x < 3} |
| M = {1, 8, 27, 64, 125.......} | M={x | x = n3, 1 ≤ n ≤ 5} |
Types of sets :
| Name of set | Definition | Example |
| Singleton Set | A set consisting of a single element is called a singleton set. | A = {2}, A is the set of even prime numbers. |
| Empty Set or Null Set | If there is not a single element in the set which satisfies the given condition then it is called a Null set or an empty set. Null set is represented by { } or a symbol Φ (phi) | B = {x | x is natural number between 2 and 3.}
∴ B = { } or Φ |
| Finite Set | If a set is a null set or number of elements are limited and countable then it is called as ‘Finite set’. | C = {p | p is a number from 1 to 22 divisible by 4.}
C = {4, 8, 12, 16, 20} |
| Infinite Set | If number of elements in a set is unlimited and uncountable then the set is called ‘Infinite set’. | N = {1, 2, 3, . . . } |
Q. Write the following sets using listing method and classify into finite or infinite set.
(i) D = {(a, b) | a, b ∈ W, a + b = 9}
Given : a and b are whole numbers and a + b = 9.
Let us first write the value of a and then the value of b such that a + b = 9.
By keeping this order set D can be written as
D = {(0, 9), (1, 8), (2, 7), (3, 6), (4, 5), (5, 4), (6, 3), (7, 2), (8, 1), (9, 0)},
In this set, number of pairs are finite and could be counted
∴ Set D is a finite set.
(ii) E = {x | x ∈ I, x2 = 100}
E = {−10, 10}. ∴ E is a finite set
(iii) F = {(a, b ) | a, b ∈ Q, a +b = 11 }
Given : a and b is a rational number, and a + b = 11
Let us first write the value of a and then the value of b such that a + b = 11.
By keeping this order set F can be written as
F = {(6, 5), (3, 8), (3.5, 7.5), (-15, 26),. . .} infinitely many such pairs can be written.
∴ F is an infinite set.
| Remember : N, W, I, Q, R all these sets are infinite sets. |
Equal sets :
If two sets contain exactly the same elements, then these sets are said to be equal sets.
- A and B are equal sets is written symbolically as A = B.
- If sets A and B are not equal, we write this as A ≠ B.
Examples :
(i) A = {x | x is a letter in the word ‘smile’}
B = {y | y is a letter in the word ‘miles’}
The sets A and B contain the same elements.
∴ A = B.
(ii) A = {3, 5, 7, 9} and B = {2, 4, 6, 8}
The number of elements in the sets A and B are equal, but the elements are not exactly the same.
∴ A ≠ B.
Venn diagrams :
- John Venn, a British logician, was the first to utilise closed figures to represent sets. Such representations are called 'Venn diagrams'.
- Venn diagrams are particularly useful for understanding and illustrating the relationship between sets, and to solve the examples based on the sets.
Examples :
(i) Set A = { 1, 2, 3, 4, 5}
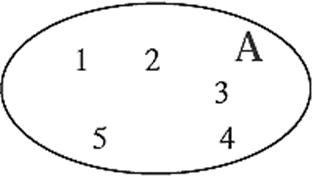
(ii) Set B = {x | -10 ≤ x ≤ 0, x is an integer}
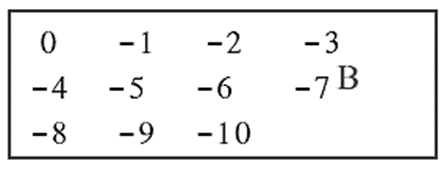
Subset :
If A and B are two given sets and every element of set B is also an element of set A then B is a subset of A which is symbolically written as B ⊆ A. It is read as 'B is a subset of A' or 'B subset A'.
Example : A = {1, 2, 3, 4, 5, 6, 7, 8}, B = {2, 4, 6, 8}
Every element of set B is also an element of set A.
Here, the set B is a subset of the set A.
∴ B ⊆A.
The concept of subset is well illustrated in the given Venn diagram
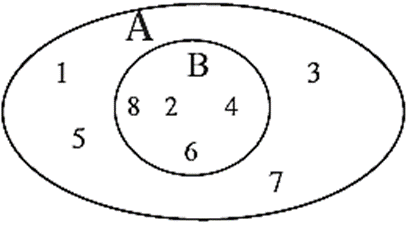
Remember :
|
Examples :
(1) N = set of natural numbers. I = set of integers.
Here N ⊆ I. because all natural numbers are integers..
(2) P = { x | x is square root of 25} S = { y | y ⊆ I, —5 ≤ y ≤ 5}
P = {—5, 5}
S = {—5, —4, —3, —2, —1, 0, 1, 2, 3, 4, 5}
Here every element of set P is also an element of set S.
∴ P ⊆ S
Q. Some sets are given below :
A= {…,—4, —2, 0, 2, 4, 6, …. }
B = {1, 2, 3, ….}
C = {..., —12, —6, 0, 6, 12, 18, ….}
D = {..., —8, —4, 0, 4, 8, ….}
I = {….., —3, —2, —1, 0, 1, 2, 3, 4, ….}
Discuss and decide which of the following statements are true.
(i) A is a subset of sets B, C and D.
(ii) B is a subset of all the sets which are given above.
(i) A is not the subset of sets B, C and D.
Hence, statement is false.
(ii) B is not the subsets of A, C and D.
B is the subset of only Set I.
Hence, statement is false.
[Set A is of even integers. Set B is of natural numbers. Set C is of integers multiple of 6. Set D is of integers multiples of 4. Set I is a set of integers.]
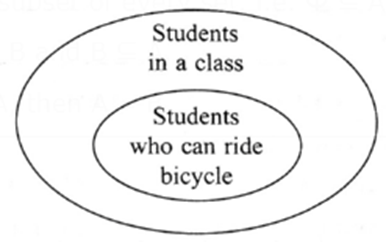
Activity :
Set of students in a class and set of students in the same class who can swim, are shown by the Venn diagram. Observe the diagram and draw Venn diagrams for the following subsets.
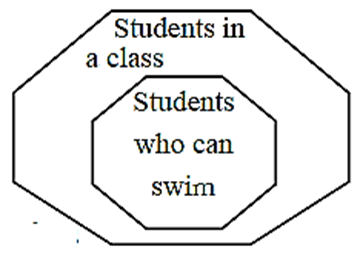
(1) (i) set of students in a class
(ii) set of students who can ride bicycles in the same class
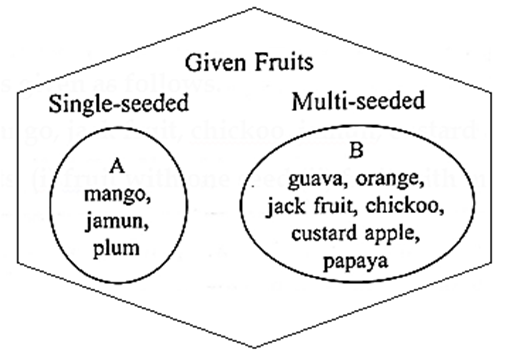
(2) A set of fruits is given as follows. {guava, orange, mango, jack fruit, chickoo, jamun, custard apple, papaya, plum}
Show these subsets. (i) fruit with one seed (ii) fruit with more than one seed.
(3) Every student should take 9 triangular sheets of paper and one plate. Numbers from 1 to 9 should be written on each triangle. Everyone should keep some numbered triangles in the plate. Now the triangles in each plate form a subset of the set of numbers from 1 to 9.
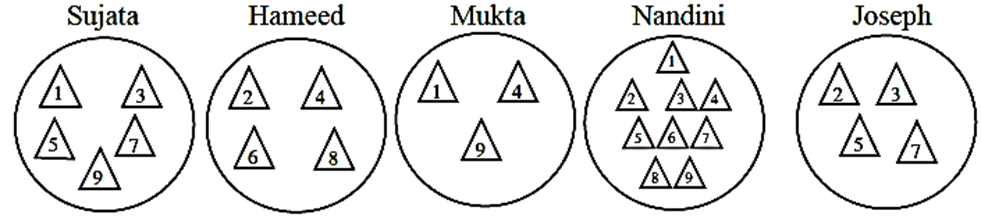
Look at the plates of Sujata, Hameed, Mukta, Nandini, Joseph with the numbered triangles. Guess the thinking behind selecting these numbers. Hence write the subsets in set builder form.
- Sujata : S = {x | x is an odd natural number. 1 ≤ x ≤ 9 }
- Hameed : H = {x | x is an even natural number. 1 ≤ x ≤ 9 }
- Mukta : M = {x | x = n2, n ∈ N, n ≤ 3}
- Nandini : N = {x | x ∈ N, 1 ≤ x ≤ 9}
- Joseph : J = {x | x is a prime number between 1 and 10}
Universal set :
Definition : A suitably chosen non-empty set, of which all the sets under consideration are the subsets of that set, is called the universal set.
- The universal set is denoted by ‘U’. It is generally represented by a rectangle in a Venn diagram.
Example : A cricket team of 15 students is to be selected from a school. Here all the students from school who play cricket is the Universal set. A team of 15 cricket players is a subset of that Universal set.

Complement of a set :
Let U be the universal set. If B is a subset of the set U (i.e. B ⊆ U), then the set of elements of U which are not contained in the set B, is called the complement of set B and is denoted by B’ or Bc.
B’ is defined as follows.
B’ = {x | x ∈ U, and x ∉ B}
Examples :
(1) U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {2, 4, 6, 8, 10}
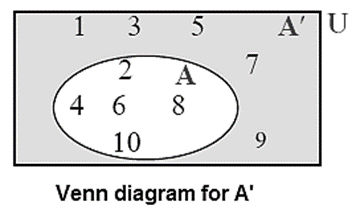
∴ A’ = {1, 3, 5, 7, 9}
The complement of set A’ is the set A itself.
[(A’)’= A.]
Properties of complement of a set :
|
Operations on sets :
Intersection of two sets
If A and B are two sets. Then the set of all common elements of A and B is called the intersection of set A and B.
It is denoted as A ∩ B and read as A intersection B.
∴ A ∩ B = {x | x ∈ A and x ∈ B}
Examples :
(i) A = { 1, 3, 5, 7} B = { 2, 3, 6, 8}
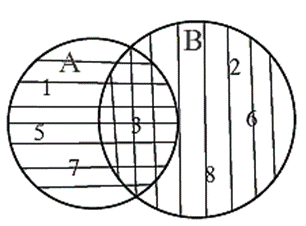
The element 3 is common in set A and B.
∴ A ∩ B = {3} and B ∩ A = {3}
(ii) A= {x, u, v, w}, B = {x, y, z}
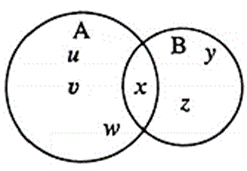
∴ A ∩ B = {x} and B ∩ A= {x}
Properties of Intersection of sets :
|
Disjoint sets :
If the two sets have no common element, then the two sets are said to be disjoint sets.
Examples : A= {3, 5, 7, 11} and B = {l, 4, 6, 8}.
Here, A ∩ B = Φ,
∴ the sets A and B are disjoint sets.
Q. (i) Observe the set A, B, C given by Venn diagrams and write which of these are disjoint sets.
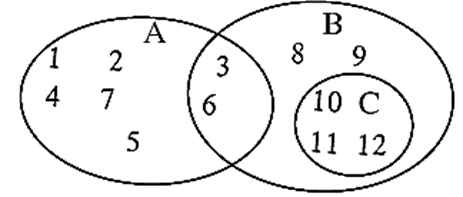
A= {1, 2, 4, 7, 5, 3, 6}
B = {8, 9, 3, 6, 10, 11, 12}
C = {10, 11, 12}
Sets A and C are disjoint sets, because there is not a single element common in these sets. Here, A ∩ C = Φ,
Q. (ii) Let the set of English alphabets be the Universal set. The letters of the word 'LAUGH' is one set and the letter of the word 'CRY' is another set. We can say that these are two disjoint sets. Observe that intersection of these two sets is empty.
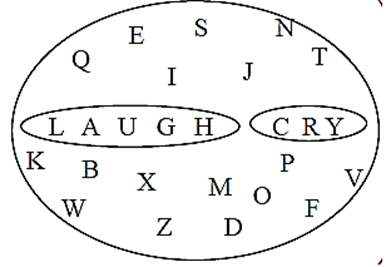
Set A = {L A, U, G, H}
Set B = {C, R, Y}
These two sets do not have any common elements.
A ∩ C = Φ,
Union of two sets :
The union of two sets A and B is a set which consists of all the elements of set A and all the elements of set B.
We write such a set as A ∪ B and read it as ‘A union B’.
Symbolically, A ∪ B = {x|x ∈ A or/and x ∈ B }.
In other words, A ∪ B = {x | x belongs to at least one of the sets A and B.}
Examples :
(1) A = {-1, -3, -5, 0}, B = {0, 3, 5}
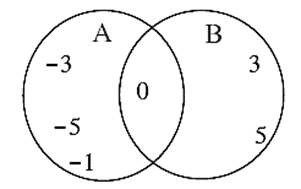
A ∪ B = {-3, -5, 0, -1, 3, 5}
Note that, A ∪ B = B ∪ A
(2) A = {1, 2, 3, 4, 5}, B = {2, 3}
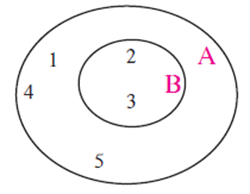
A ∪ B = {1, 2, 3, 4, 5}
Hence, if B ⊆ A then A ∪ B = A
Properties of Union of sets :
|
Number of elements in a set
Let A = {3, 6, 9, 12,15} is a given set with 5 elements.
Number of elements in set A is denoted as n (A). ∴ n (A) = 5 …..(1)
Let B = { 6, 12, 18, 24, 30, 36} ∴ n (B) = 6 …..(2)
The number of elements in the union of sets and the intersection of sets.
Consider the above sets A and B.
n(A) + n(B) = 5 + 6 = 11 …..(3)
[From (1) and (2)]
A∪ B = {3, 6, 9, 12, 15, 18, 24, 30, 36} ∴ n(A ∪ B) = 9 ……(4)
A ∩ B = {6, 12} ∴ n(A ∩ B) = 2 …..(5)
From (3) and (5),
n(A) + n(B) — n(A ∩ B) = 5 + 6 —2 = 9 …..(6)
From (4) and (6),
n(A ∪ B) = n(A) + n(B)—n(A ∩ B) ……(7)
Observe the given Venn diagram to verify (7).
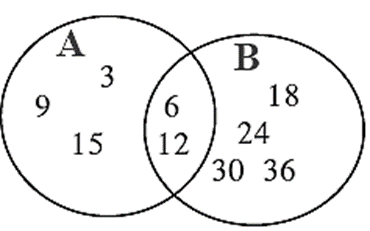
n(A) = 5, n(B) = 6, n(A ∩ B) = 2, n(A ∪ B) = 9
n(A ∪ B) = n(A) + n(B) — n(A ∩ B)
Word problems based on sets :
Q. In a class of 70 students, 45 students like to play Cricket. 52 students like to play
Kho-kho. All the students like to play atleast one of the two games. How many students like to play Cricket or Kho-kho ?
Example can be solve in two ways.
Method I : Total number of students = 70
Let A be the set of students who likes to play Cricket.
Let B be the set of students who likes to play Kho-kho.
Hence the number of students who likes to play Cricket or Kho-kho is n (A ∪ B )
∴ n (A ∪ B ) = 70
Number of students who likes to play both Cricket and Kho-kho = n (A ∩ B)
n (A) = 45, n (B) = 52
We know, n (A ∪ B ) = n (A) + n (B) - n (A ∩ B) .
∴ n (A ∩ B) = n (A) + n (B) - n (A ∪ B ) = 45 + 52 - 70 = 27
∴ Number of students who likes to play both the games are 27,
Number of students who likes to play Kho-kho are 45.
∴ Number of students who likes to play only Cricket = 45 - 27 = 18
∴ A ∩ B is the set of students who play both the games. ∴ n (A ∩ B)= 27
Method II : Given information can be shown by Venn diagrams as follows.
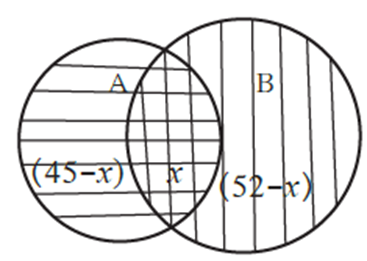
Let n (A ∩ B) = x, n (A) = 45, n (B) = 52,
We know that, n (A ∪ B ) = 70
∴ n (A ∩ B) = x = n (A) + n (B) - n (A ∪ B) = 52 + 45 - 70 = 27
Students who like to play only cricket = 45 – 27 =18
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 9th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Next Chapter : Chapter-2-Real Numbers – Online Notes