Circle
Class-10-Mathematics-2-Chapter-3-Maharashtra Board
Notes Part-1
|
Topics to be learn : Part -1
|
Introduction :
Circle : The set of points equidistant from a fixed point in a plane is a circle.
The fixed point is called the centre of the circle. In the figure, O is the centre of the circle.
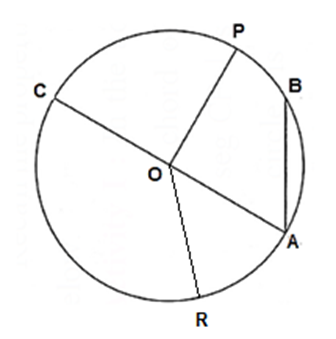
- Radius : The segment joining the centre of the circle and a point on the circle is called the radius of the circle. Seg OP or OR is the radius. Circle can have infinite radii. Radii of the same circle are congruent.
- Chord : The segment joining any two points of the circle is called a chord. In the figure seg AB is the chord. Circle can have infinite chords.
- Diameter : The chord which passes through the centre of a circle is the diameter. Diameter is the longest chord of the circle. Diameter is twice the radius. A circle can have infinite diameters.
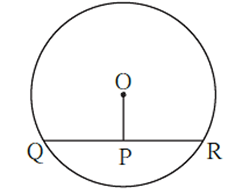
Statement : A perpendicular drawn from the centre of a circle on its chord bisects the chord.
In the figure, if O is the centre of the circle, seg OP ⊥ chord QR and Q—P—R; then QP = PR.
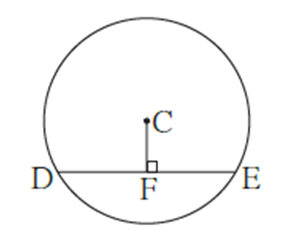
Example : In the adjoining figure, seg DE is a chord of a circle with centre C. seg CF ⊥ seg DE. If diameter of the circle is 20 cm, DE = 16 cm, find CF.
Solution :
Join CE in figure
Given : seg CF ⊥ seg DE, Diameter = 20 cm, DE = 16 cm
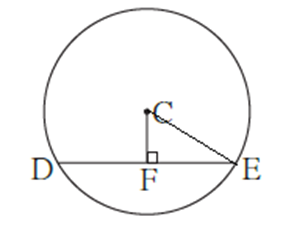
A perpendicular drawn from the centre of a circle on its chord bisects the chord.
∴ FE = DE/2 = 16/2 = 8 cm
Diameter of the circle is 20 cm
∴ CE = Dia/2 = 10 cm = Radius of circle
CE2 = CF2 + FE2 ….(Pythagoras Therom)
102 = CF2 + 82
100 = CF2 + 64
∴ CF2 = 100 – 64 = 36
∴ CF = 6 cm
Statement : The segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord.
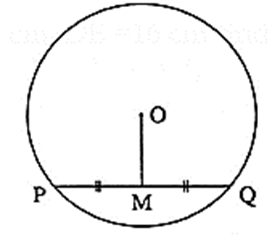
In the figure,
If O is the centre of the circle, M is the midpoint of chord PQ, then seg OM ⊥ chord PQ.
i.e. ∠ OMP = ∠ OMQ = 90°.
Statement : Congruent chords of a circle are equidistant from the centre of the circle.
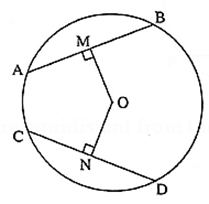
In the figure, O is the centre of the circle. If chord AB ≅ chord CD,
seg OM ⊥ chord AB and seg ON ⊥ chord CD such that A—M—B and C-N-D then OM = ON.
Statement : The chords of a circle equidistant from the centre of a circle are congruent.
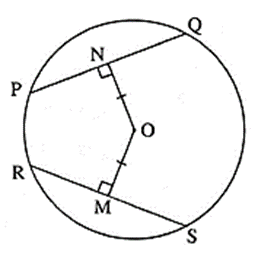
In the figure,
O is the centre of the circle. seg PQ and seg RS are chords.
seg OM ⊥ chord RS and seg ON ⊥ chord PQ
such that R-M-S and P—N—Q.
If OM = ON, then chord PQ ≅ chord RS
Circles passing through one, two, three points :
- Infinite number of circles can pass through one point.
- Infinite circles pass through two distinct points.
- There is one and only one circle (i.e. unique circle) passing through three non-collinear points.
- No circle can pass through three collinear points.
Secant and tangent :

- Line m and the circle have one and only one point P in common as shown in figure. Such a line is called the tangent of the circle and the common point is called the point of contact.
- In the figure, point P is the point of contact.
- In the figure, line l and the circle have two points in common. Such a line is called as a secant of the circle.
- Points Q and R are the points of intersection of the circle and the secant.
- In the figure, if we draw the radius BP, it will be perpendicular to line m.
- This concept is known as Tangent theorem.
Tangent theorem :
Theorem : A tangent at any point of a circle is perpendicular to the radius at the point of contact.
Given :
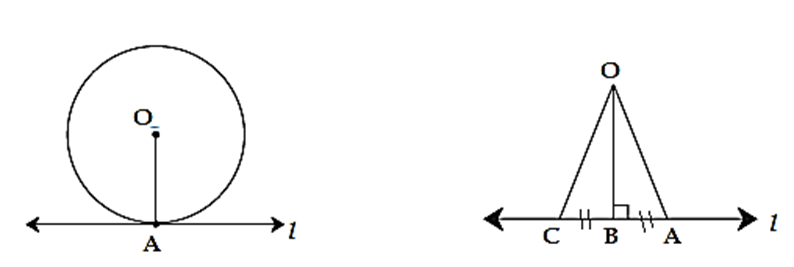
(i) A circle with centre O , (ii) Line l is tangent to the circle at point P.
To prove : Line l ⊥ radius OP
Proof : (There is an indirect proof of this theorem.)
Assume that, line l is not perpendicular to seg OA.
Suppose, seg OB is drawn perpendicular to line l.
Of course B is not same as A.
Now take a point C on line l such that A-B-C and BA = BC .
Now in, ΔOBC and ΔOBA
seg BC ≅ seg BA ........ (construction)
∠ OBC ≅ ∠ OBA ....... (each right angle)
seg OB ≅ seg OB
∴ ΔOBC ≅ ΔOBA .......... (SAS test)
∴ OC = OA
But seg OA is a radius.
∴ seg OC must also be radius.
∴ C lies on the circle.
That means line l intersects the circle in two distinct points A and C.
But line l is a tangent. ........... (given)
∴ it intersects the circle in only one point.
Our assumption that line l is not perpendicular to radius OA is wrong.
∴ line l ⊥ radius OA.
Converse of tangent theorem :
Theorem: A line perpendicular to a radius at its point on the circle is a tangent to the circle.
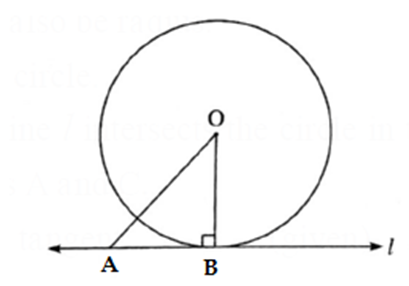
Given : (i) A circle with centre O , (ii) seg OB is the radius (iii) Line l ⊥ radius OB at point B.
To prove : line l is a tangent to the circle.
Proof : Take a point A on line l, other than B. Draw seg OA.
In Δ OBA, ∠ OBQ = 90°
Δ OBA is a right angled triangle.
In a right angled triangle, the hypotenuse is the largest side.
∴ OA > OB
∴ OA > radius (‘.’ OB = radius)
∴ A doesn’t lie on the circle.
This is true for all the points on line l, other than B.
∴ only point B is the common point between line l and the circle.
∴ line l is tangent to the circle (By definition)
Remember :·
|
Tangent segment theorem :
In the below figure line DP and line DQ touch the circle at points P and Q.
Seg DP and seg DQ are called tangent segments.

Theorem : Tangent segments drawn from an external point to a circle are congruent.
Given : (i) A circle with centre A. (ii) Lines DP and DQ are tangents to the circle at points P and Q respectively.
To prove : seg DP ≅ seg DQ
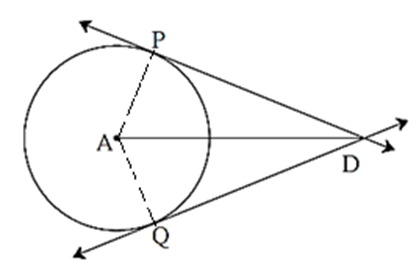
Construction : Draw seg AD, seg AP and seg AQ
Proof: In Δ APD and Δ AQD,
∠ APD = ∠ AQD = 90° (Tangent theorem)
Hypotenuse AD ≅ Hypotenuse AD (Common side)
side AP ≅ side AQ (Radii of the same circle)
∴ Δ APD ≅ Δ AQD (Hypotenuse side test)
∴ seg DP ≅ seg DQ (c.s.c.t.)
Remember :·
|
Solved Examples :
Q. 1 In the adjoining figure circle with centre D touches the sides of ∠ ACB at A and B. If ∠ ACB = 52°, find measure of ∠ ADB.

The sum of all angles of a quadrilateral is 360°.
∴ ∠ ACB + ∠ CAD + ∠ CBD + ∠ ADB = 360°
∴ 52° + 90° + 90° + ∠ ADB = 360° ............. Tangent theorem
∴ ∠ ADB + 232° = 360°
∴ ∠ ADB = 360° - 232° = 128°
Touching circles :
- If two circles in the same plane intersect with a line in the plain in only one point, they are said to be touching circles and the line is their common tangent.
- The point common to the circles and the line is called their common point of contact.
- Circles can touch each other internally or circles can touch each other externally.
- In figure 1, the circles with centres X and Z touch each other externally at point Y. Line l is the common tangent at point Y.
- In figure 2, the circles with centre X and Z touch each other internally at point Y. Line l is the common tangent at point Y.
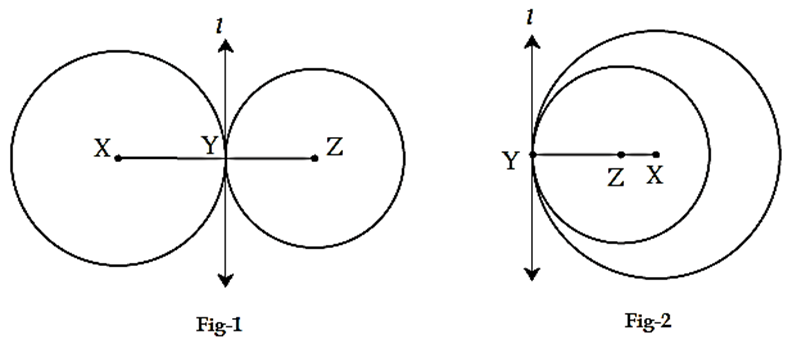
- When circles touch each other externally, the centres lie on the opposite side of the common tangent.
- Whereas, when circles touch each other internally, the centres lie on the same side of the common tangent.
Theorem of touching circles :
Theorem : If two circles touch each other, their point of contact lies on the line joining their centres.
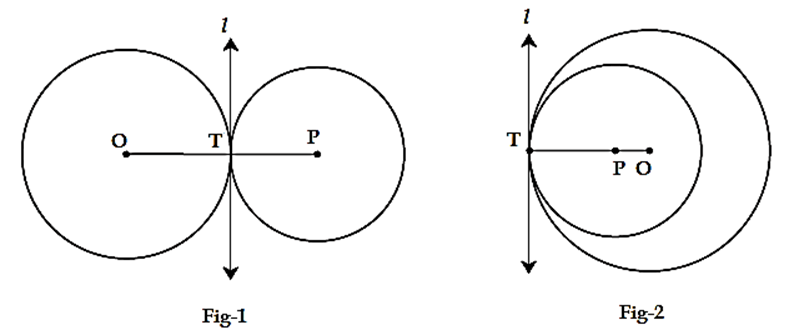
Given : Two circles with centres O and P touch each other at point T.
To prove : Point T lies on line OP.
Construction : Draw seg OT, seg PT and common tangent l at point T.
Proof : seg OT ⊥ line l , seg PT ⊥ line l …. (Tangent theorem)
∴ seg OT and seg PT are perpendiculars to line l at point T.
‘.’ one and only one perpendicular can be drawn at a given point on a line.
∴ lines OT and PT are not two different lines.
They are one and the same.
∴ points O, T and P are collinear.
∴ point T lies on line OP.
Remember :·
Arc of a circle :
- A secant divides a circle in two parts. Each part together with the points common to the circle, is called an arc. An arc is a part of a circle.
- The points of intersection of circle and secant are called the end points of the arcs.
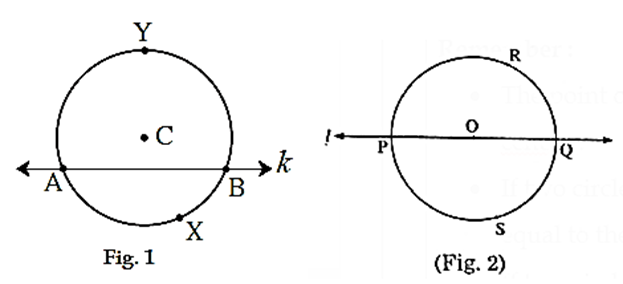
- In the figure 1, secant k intersects the circle at points A and B. Arc AXB and arc AYB are thus two arcs formed due to secant k.
- If the secant passes through the centre, each arc so formed is a semicircle.
- In the figure 2, line l passes through centre O intersecting the circle at points P and Q. Seg PQ is the diameter. Arc PRQ and arc PSQ are semicircles.
- In the figure 1, line k doesn’t pass through the centre. The arc on the side of the centre is the major arc and arc on the other side of the centre is the minor arc. Arc AYB is the major arc and arc AXB is the minor arc.
Naming an arc :
- Usually three points are used to name an arc. The first and the last points in naming an arc are always its endpoints.
- In the figure 1, arc AXB and arc AYB have endpoints A and B. The minor arc is named AXB and major arc is named AYB.
- In case, if an arc is denoted with two points then it is always the minor arc.
Central Angle : An angle in the plane of the circle with its vertex at the centre is called central angle.
In the figure, O is the centre of the circle and ∠ AOB is the central angle.
Like secant, a central angle also divides a circle into two arcs.
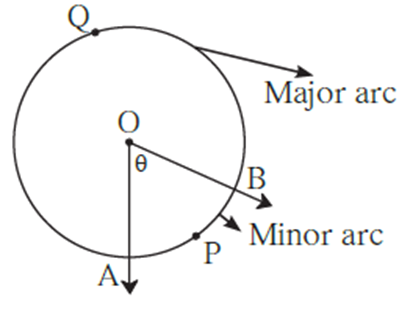
Measure of an arc :
To compare two arcs, we need to know their measures. Measure of an arc is defined as follows
- m(arc APB) denotes the measure of arc APB
- Measure of a minor arc is equal to the measure of its corresponding central angle.
- In the above figure, O is the centre of the circle and arc APB is minor arc. Arc AQB is major arc.
- Here m(arc APB) = ∠ AOB = θ.
- Measure of major arc = 360° − measure of corresponding minor arc
- Here m(arc AQB) = 360° − m(arc APB).
- Measure of a semicircular arc, that is of a semicircle is 180°.
- Measure of a circle is 360°.
Congruence of arcs :
Two arcs are congruent if their measures and radii are equal.
Or
Two arcs of the same circle or of congruent circles, having equal measures, are congruent.
- In below figure ‘Arc DE and arc GF are congruent’ is written in symbol as arc DE ≅ arc
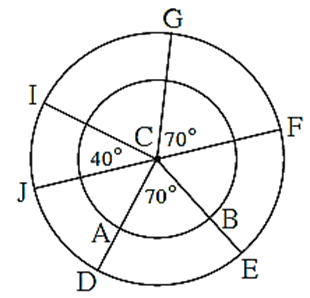
Property of sum of measures of arcs
In below figure the points A, B, C, D, E are concyclic. With these points many arcs are formed.
There is one and only one common point C to arc ABC and arc CDE.
So measure of arc ACE is the sum of measures of arc ABC and arc CDE.
m(arc ABC) + m(arc CDE) = m(arc ACE)
But arc ABC and arc BCE have many points in common. [All points on arc BC.]
So m(arc ABE) ≠ m(arc ABC) + m(arc BCE).
Theorem : The chords corresponding to congruent arcs of a circle ( or congruent circles) are congruent.
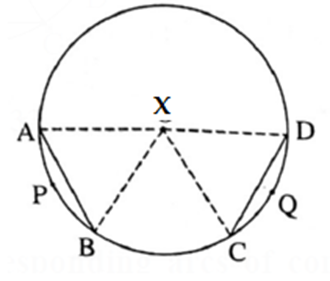
Given : (i) A circle with centre X., (ii) Arc APB ≅ arc CQD.
To prove : Chord AB ≅ chord CD.
Construction : Draw seg XA, seg XB, seg XC and seg XD.
Proof :
m (arc APB) = ∠ AXB ...(1) …(Definition of measure of minor arc)
m(arc CQD) = ∠ CXD …(2) …(Definition of measure of minor arc)
arc APB ≅ arc CQD …(Given)
∴ m(arc APB) = m(arc CQD)
∴ ∠ AXB ≅ ∠ CXD ……[From (1) and (2)] ….(3)
In Δ AXB and Δ CXD,
seg XA ≅ seg XC ……(Radii of the same circle)
∠ AXB ≅ ∠ CXD ….[From (3)]
seg XB ≅ seg XD …….(Radii of the same circle)
∴ ∠ AXB ≅ ∠ CXD ……(SAS test of congruence)
∴ seg AB ≅ seg CD ……(corresponding sides of congruent triangle.)
i.e. chord AB ≅ chord CD.
Theorem: Corresponding arcs of congruent chords of a circle (or congruent circles) are congruent.

Given : (i) A circle with centre O. (ii) Chord AB ≅ chord CD.
To prove : Arc AMB ≅ arc CND.
Construction : Draw seg OA, seg OB, seg OC and seg OD.
Proof : In Δ AOB and Δ COD,
seg OA ≅ seg OC ….. (Radii of the same circle)
seg OB ≅ seg OD ….. (Radii of the same circle)
seg AB ≅ seg CD …….(Given)
∴ Δ AOB ≅ Δ COD (SSS test of congruence)
∴ ∠ AOB ≅ ∠ COD ………(c.a.c.t.) ….(1)
m(arc AMB) = ∠ AOB …...(Definition of measure of minor arc)… (2)
m(arc CND) = ∠ COD …...(Definition of measure of minor arc)… (3)
∴ m(arc AMB) = m(arc CND) …… [From (1), (2) and (3)]
∴ arc AMB ≅ arc CND.
Solved Example :
Q. 1- A, B, C are any points on the circle with centre O.
(i) Write the names of all arcs formed due to these points.
(ii) If m arc (BC) = 110° and m arc (AB) = 125°, find measures of all remaining arcs.
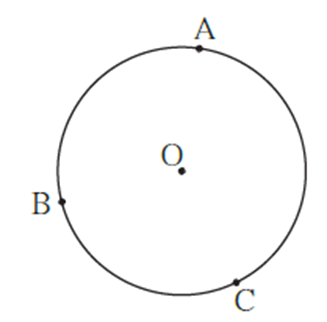
(i) Names of arcs - arc AB, arc BC, arc AC, arc ABC, arc ACB, arc BAC
(ii) m(arc ABC) = m(arc AB) + m(arc BC)
= 125° + 110° = 235°
m (arc AC) = 360° − m (arc ABC)
= 360° − 235° = 125°
Similarly, m(arc ACB) = 360° − m(arc AB)
= 360° − 125° = 235°
and m(arc BAC) = 360° − m(arc BC)
= 360° − 110° = 250°
Q. 2- In the below figure, a rectangle PQRS is inscribed in a circle with centre T.
Prove that, (i) arc PQ ≅ arc SR (ii) arc SPQ ≅ arc PQR
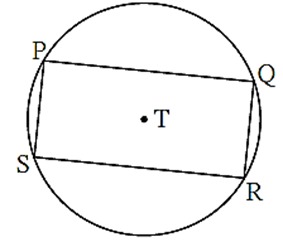
(i) c PQRS in a rectangle.
∴ chord PQ ≅ chord SR ....... opposite sides of a rectangle
∴ arc PQ ≅ arc SR ...... arcs corresponding to congruent chords.
(ii) chord PS ≅ chord QR ..... Opposite sides of a rectangle
∴ arc SP ≅ arc QR ..... arcs corresponding to congruent chords.
∴ measures of arcs SP and QR are equal
Now, m(arc SP) + m(arc PQ) = m(arc PQ) + m(arc QR)
∴ m(arc SPQ) = m(arc PQR)
∴ arc SPQ ≅ arc PQR
Remember :
PDF-Notes,Solution,Text Book
Main Page : – Maharashtra Board Class 10th-Mathematics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-2-Pythagoras Theorem – Online Notes
Next Chapter : Chapter-4-Geometric Construction – Online Notes