Laws of Motion
Maharashtra Board-Class-11-Science-Physics-Chapter-4
Notes-Part-2
Topics to be Learn : Part-2
|
Work Energy Theorem:
Work-kinetic energy theorem : If there is a decrease in the potential energy due to a conservative force, it is entirely converted into kinetic energy i.e. when work done on a body changes only the speed of the body, the work done by the net force equals the change in the kinetic energy of the body.
Explanation : According to the theorem, net work done on a particle
= change in the kinetic energy of the particle
= final KE — initial KE
- A force does positive work when it has a component in the same direction as the displacement and it does negative work when it has a component opposite to the displacement.
- It does zero work when it has no component along the displacement, i.e., when it is perpendicular to the displacement.
- Then, the work-kinetic energy theorem indicates that if the net work done on a particle is positive, the speed of the particle increases because the final kinetic energy is greater than the initial kinetic energy.
- If the net work is negative, the speed decreases because the final kinetic energy is less than the initial kinetic energy.
Proof : Change in kinetic energy is equal to work done by the conservative force.
Consider an object of mass m moving with velocity \(\vec{u}\) experiencing a constant opposing force \(\vec{F}\) which slows it down to \(\vec{v}\) during displacement \(\vec{s}\)
As \(\vec{u}\) and \(\vec{F}\) are oppositely directed, the entire motion will be along the same line. In this case we need not use the vector form, just ± signs should be good enough.
If a = F/m is the acceleration, we can write the relevant equation of motion as
v2 − u2 = 2 (−a)s …..(1) (negative acceleration for opposing force)
The work done by force is W = (ma).s = F.s
Multiplying throughout by m/2 to eq (1), we get
½ mu2 – ½ mv2 = (ma).s = F.s
Left-hand side is decrease in the kinetic energy and the right-hand side is the work done by the force. Thus, change in kinetic energy is equal to work done by the conservative force, which is in accordance with work-energy theorem.
.
Q. Show that total mechanical energy is conserved in a conservative force field.
Ans. The total mechanical energy (E) of a particle, or a system, is the sum of the kinetic and potential energies of the particle or the system at any moment.
E = KE + PE
By the work-energy theorem, the work done by a conservative force W = Δ KE.
Also, the change in potential energy associated with a conservative force is the negative of the work done by that force.
W = − ΔPE = ΔKE
ΔKE + ΔPE = 0
(KE2 − KE1) + (PE2 − PE1) = 0
where the subscripts denote some initial time 1 and any later time 2.
∴ KE2 + PE2 = KE1+ PE1
∴ E2 = E1 = constant
That is, the total mechanical energy of a particle or system is conserved in the absence of dissipative forces.
.
Work-energy theorem of a non-conservative force :
The work done by a non-conservative force, unlike that by a conservative force, depends on the particular path during a displacement. In the presence of a non-conservative force, the work-energy theorem has to be suitably modified :
Suppose a conservative force and a non-conservative force act on a body during a displacement Δs. The total (net) work W is the sum of the Work done Wc by the conservative force and the work done Wnc by the non-conservative force.
W = Wc + Wnc
By the work-energy theorem,
W = ΔKE (change in KE)
and the work done by a conservative force can be written in terms of the appropriate potential energy :
Wc = −ΔPE (negative change in PE)
∴ Wnc = W − Wc = ΔKE + ΔPE = ΔE
where ΔE = ΔKE + ΔPE is the change in the total mechanical energy.
Principle of conservation of linear momentum :
Principle or law of conservation of linear momentum : When the resultant external force acting on a system is zero, the total linear momentum of the system is constant i.e., it is conserved. OR The total linear momentum of an isolated system, i.e., a system subject only to internal forces, is constant i.e., it is conserved.
The principle is a consequence of Newton's third law of motion.
Examples :
(1) As a person jumps out of a stationary boat, the boat moves in the backward direction. Initially, the momentum of the system was zero because both of them were at rest. While jumping, the forward momentum of the person must be equal in magnitude to the backward momentum of the boat such that their sum is zero and the total linear momentum of the person and boat is conserved.
(2) When a bomb explodes in mid-air, the fragments fly off in different directions However, it is found that the vector sum of the momenta of all the fragments at any instant always remains equal to the initial momentum of the bomb in both magnitude and direction. Here, there is an increase in KE and production of heat, sound and light because the chemical PE of its explosive ingredients is partly converted to these forms.
(3). Rocket propulsion depends on the law of conservation of momentum as applied to a system consisting of the rocket and the exhaust gases. Most of a rocket on its launching pad is oxygen and fuel, all of which is eventually burnt to accelerate the small payload. Exhaust gases (combustion products) are ejected at very high speed from the nozzle at the tail end of the rocket engine. Because of the momentum of the ejected gases, the rocket receives a compensating momentum in the opposite direction to conserve the original momentum of the rocket-gas system.
Remember This :
|
Free-body diagram : When solving problems involving forces and Newton's laws of motion, a diagram showing all the forces acting on each object involved is called a free-body diagram or force diagram.
For one object, vectors are drawn to represent every force acting on the object. If there are multiple objects, a separate free-body diagram is needed for each object.
Collisions:
During collisions a number of objects come together, interact (exert forces on each other) and scatter in different directions.
Principle or law of conservation of linear momentum from Newton's laws of motion :
Consider the collision of two particles of masses m1 and m2, moving before the collision with constant velocities \(\vec{u_1}\) and \(\vec{u_2}\) in the laboratory frame of reference, see below Fig. After the collision they have velocities \(\vec{v_1}\) and \(\vec{v_2}\), again considered to be constant.

We shall assume that there are no external forces on the two particle system and the contact forces, which the particles exert on one another, act only over the short time interval Δt for which the particles are in contact during collision. The contact forces during collision act only between the particles of the system : they are internal forces of the system as distinguished from external forces which originate in bodies not belonging to the system.
Then, during the collision, particle 1 exerts a force F21 (Fon 2 by 1) on particle 2. The impulse \(\vec{F}_{21}\)Δt on particle 2 changes its linear momentum from to
\(\vec{F}_{21}\)Δt = \(m_2\vec{v_2} - m_2\vec{u_2}\) ……..(1)
(from Newton's second law of motion.)
By Newton's third law of motion, particle 2 simultaneously exerts a reaction force \(\vec{F}_{12}\)
(\(\vec{F}_{on\,1\,by\,2}\) ) on particle 1
\(\vec{F}_{12}\) = \(-\vec{F}_{21}\) ……(2)
The impulse \(\vec{F}_{12}\)Δt on particle 1 changes its linear momentum from \(m_1\vec{u_1}\) to \(m_1\vec{v_1}\) :
\(\vec{F}_{12}\)Δt = \(m_1\vec{v_1} - m_1\vec{u_1}\) ……..(2)
From Eqs. (1), (2) and (3),
\(\vec{F}_{12}\)Δt = \(-\vec{F}_{21}\)Δt
Or
\(m_1\vec{v_1} - m_1\vec{u_1}\) = \(-m_2\vec{v_2} - m_2\vec{u_2}\)
Which on arranging gives
\(m_1\vec{v_1} + m_2\vec{v_2}\) = \(m_1\vec{u_1} + m_2\vec{u_2}\)
∴ [Total momentum after collision] = [Total momentum before collision]
Thus, if two particles interact only with one another, i.e., there is no external force on the system of two particles, then their total linear momentum is conserved, which is the principle or law of conservation of linear momentum.
This principle holds good even when the number of particles involved is more than two.
Elastic collision : If in a collision of two particles, the total kinetic energy of the particles is conserved along with the total linear momentum and the total energy, the collision is said to be elastic.
- An elastic collision is impossible in daily life. However, in many situations, the interatomic or intermolecular collisions are considered to be elastic
Examples :
- At normal temperatures, the collisions between molecules of a gas are usually elastic.
- Collisions between atomic particles like electrons, protons or neutrons are elastic provided they do not have very high energy or do not become bound together in the interaction.
Inelastic collision : A collision is said to be inelastic if there is a loss in the kinetic energy during collision, but linear momentum is conserved.
- In an inelastic collision, the total kinetic energy of the colliding particles after collision is, usually, less than the initial total kinetic energy due to transformation to some other form of energy such as heat, sound, etc.
- The final kinetic energy of the system may be greater than the initial kinetic energy, due to the release of some form of energy. Such collisions are sometimes called explosive.
- Examples : A collision between two vehicles, a bat and a ball.
- The collisions of any two macroscopic objects is always inelastic because some mechanical energy is always converted into heat, sound or used to produce deformations.
Perfectly inelastic collision : A perfectly inelastic collision of two particles is an extreme type of inelastic collision in which the two colliding particles stick together after the collision. This is a special case of inelastic collisions.
- The loss in kinetic energy is maximum in perfectly inelastic collision.
Examples :
- If mud or clay is dropped, it sticks to the surface. This is perfectly inelastic collision.
- A bullet fired at a wooden block gets embedded in the wood and the two bodies move together thereafter.
Coefficient of Restitution e: When two bodies collide with each other, the negative ratio of their relative velocity after collision to their relative velocity before collision, is called the coefficient of restitution (e).
One dimensional or head-on collision: A collision is said to be head-on if the colliding objects move along the same straight line, before and after the collision.
For a head-on collision in one dimension, if u1 and u2 are the velocities before collision, and v1 and v2 are the velocities after collision, then the relative velocity of body 1 with respect to body 2 before and after the collision are
(u1 − u2) and (v1 − v2), respectively.
. e = \(-\frac{\text{relative velocity after collision}}{\text{relative velocity before collision}}\)
= \(-\frac{v_1-v_2}{u_1-u_2}\) = \(\frac{v_2-v_1}{u_1-u_2}\)
= \(\frac{\text{velocity of separation}}{\text{velocity of approach}}\)
In a head-on collision, the relative velocity of the two particles is reversed, so that e is defined in such a way as to be positive.
Explanation : In a head-on elastic collision, the velocity of separation is equal to the velocity of approach. In a perfectly inelastic collision, the velocity of separation is zero (v1 = v2).
Therefore, 1 > e ≥ 0 and e is a measure of the elasticity of the collision :
- If e = 1, the collision is elastic.
- If 1 > e ≥ 0, the collision is inelastic, with e = o for perfectly inelastic collision.
Head-on collisions between macroscopic solid objects are never elastic, and the total final kinetic energy is less than the total initial kinetic energy. The coefficient e is a measurable physical quantity and can be shown to be related to this loss of kinetic energy in a collision. The coefficient e (like coefficient of friction) depends on the materials of the bodies.
Coefficient of restitution during a head-on, elastic collision:
Consider the head-on collision of two particles of masses m1 and m2, moving before the collision with constant velocities u1 and u2 in the laboratory frame of reference (see Fig.).

After the collision they have velocities v1 and v2; again considered to be constant. Since the collision is head-on, i.e., the motion is confined to one dimension, the velocity vectors all lie in the same line and hence we can write the equations in scalar form with the usual sign convention. Therefore, by the principle of conservation of linear momentum,
m1u1 + m2u2 = m1v1 + m2v2 …..(1)
or m1(u1 − v1) = m2(v2 − u2) …..(2)
Also, since the collision is elastic, total kinetic energy before collision = total kinetic energy after collision :
½ m1u12 + ½ m2u22 = ½ m1v12 + ½ m2v22
∴ m1(u12 − v12)=m2(v22 − u22)
Or m1(u1 − v1) (u1 + v1) = m2(v2 − u2) (v2 + u2) …….(3)
Dividing Eq. (3) by Eq. (2 ), we get,
u1 + v1 = v2 + u2 …….(4)
Rearranging the terms in Eq. (4),
u1 − u2 = v2 − v1 …….(5)
Here, (u1 − u2) is the velocity with which particle 1 approaches particle 2 before collision and (v2 − v1) is the velocity with which particle 2 separates away from particle 1 after collision.
Hence, in a head-on elastic collision, velocity of separation = velocity of approach.
From Eq. (5), the coefficient of restitution,
e = \(\frac{v_2-v_1}{u_1-u_2}\) = 1
In a perfectly inelastic collision, the colliding particles stick together and move with a common velocity. That is, their velocity of separation after the collision is zero. Therefore, the coefficient of restitution,
e = \(\frac{\text{velocity of separation}}{\text{velocity of approach}}\) = 0
Thus, for an elastic collision, coefficient of restitution, e =1. For a perfectly inelastic collision, e =0 (by definition). Thus, for any collision, the coefficient of restitution lies between 1 and 0.
Expressions for final velocities after a head-on, elastic collision:
Refer upto eq. (4)
From Eq. (4),
v2 = u1 + v1 − u2
Substituting this value of v2 in Eq. (1),
m1u1 + m2u2 = m1v1 + m2(u1 + v1 − u2)
∴ u1(m1 − m2) + 2 m2u2 = (m1 + m2) v1
∴ v1 = \((\frac{m_1-m_2}{m_1+m_2})u_1+(\frac{2m_2}{m_1+m_2})u_2\)…….(6)
Similarly, from Eq. (4), v1 = u2 + v2 − u1
which on substitution into Eq. (1) gives
∴ v2 = \((\frac{2m_1}{m_1+m_2})u_1+(\frac{m_2-m_1}{m_1+m_2})u_2\) …….(7)
Particular cases:
Two particles of masses m1 and m2 move with initial velocities u1 and u2 such that particle 1 collides head-on elastically with particle 2.
Their respective velocities after the collision are
v1 = \((\frac{m_1-m_2}{m_1+m_2})u_1+(\frac{2m_2}{m_1+m_2})u_2\)
v2 = \((\frac{2m_1}{m_1+m_2})u_1+(\frac{m_2-m_1}{m_1+m_2})u_2\)
(i) If the bodies are of equal masses (or identical), m1 = m2
Substituting m1 = m2 in the above equations,
v1 = \((0)u_1+(\frac{2m_2}{2m_2})u_2\) = u2
and v2 = \((\frac{2m_1}{2m_1})u_1+(0)u_2\) = u1
This shows that in a head-on elastic collision of two particles of equal masses, the particles exchange their velocities.
Further, if the second particle is at rest before the collision, u2 = 0, so that after the collision, v1 = 0 and v2 = u1 that is, the first particle initially moving stops and the second one takes off with the initial velocity of the first.
(ii) If colliding body is much heavier and the struck body is initially at rest, i.e., m1 >> m2 and u2= 0
Then,
v1 ≅ \((\frac{m_1}{m_1})u_1\) ≅ u1
and v2 ≅ \((\frac{2m_1}{m_1})u_1\) ≅ 2u1
that is, if a massive particle makes an elastic head-on collision with a light one at rest, the massive one continues its motion at almost the same speed, and the light one takes off at nearly twice this speed.
(iii) The body which is struck is much heavier than the colliding body and is initially at rest, i.e., m1 << m2 and u2= 0
Then, ignoring m1 in comparison to m2, the final velocities are
v1 ≅ \((-\frac{m_1}{m_1})u_1\) ≅ −u1 and v2 ≅ (0)u1 ≅ 0
Thus, if a light particle makes an elastic collision with a massive one at rest, it rebounds with almost its initial speed; the massive one is almost unaffected.
Loss in the kinetic energy during a perfectly inelastic head-on collision:
Consider a perfectly inelastic, head on collision of two bodies of masses m1 and m2 with respective initial velocities u1 and u2. As the collision is perfectly inelastic, they move jointly after the collision, i.e., their final velocity is the same. Let it be v.
According to conservation of linear momentum,
m1u1 + m2u2 = (m1 + m2)v
∴ v = \(\frac{m_1u_1+m_2u_2}{m_1+m_2}\)
This is the common velocity after a perfectly inelastic collision
Loss in the kinetic energy :
Loss in K.E. = Δ (K.E.) = Total initial K.E. − Total final K.E.
= ½ (m1+m2)v2 – (½ m1u12 + ½ m2u22)
= ½ (m1+m2)\((\frac{m_1u_1+m_2u_2}{m_1+M-2})^2\) – (½ m1u12 + ½ m2u22)
= \(\frac{1}{2}[\frac{(m_1u_1+m_2u_2)^2}{m_1+m_2}-(m_1u_1^2+m_2u_2^2)]\)
= \(\frac{1}{2}[\frac{m_1u_1^2+2m_1m_2u_1u_2+m_2^2u_2^2-m_1^2u_1^2-m_2^2u_2^2-m_1m_2u_1^2-m_1m_2u_2^2}{m_1+m_2}]\)
= \(\frac{1}{2}[-\frac{m_1m_2(u_1^2+u_2^2-2u_1u_2)}{m_1+m_2}]\) = \(-\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2\)
Since the bracketed terms are always positive, the minus sign in Eq. (2) shows that the final kinetic energy is less than the initial kinetic energy. That is, there is a loss in kinetic energy.
Loss in KE = initial KE — final KE = \(\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2\)
If two particles undergo a head-on collision, then the expression for the loss in KE in terms of the masses, initial velocities and the coefficient of restitution :
Consider a one-dimensional (head-on) collision of two particles, of masses m1 and m2, moving with constant initial velocities u1 and u2. If the coefficient of restitution is e, it can be shown that
Loss in KE = \(\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2(1-e^2)\)
Since 0 ≤ e ≤ 1, (1 — e2) is either zero or positive.
The term (u1 — u2)2 on the right hand side is always positive. Hence, for 0 <e < 1, i.e., an inelastic collision, there is always a loss in kinetic energy.
(i) For an elastic collision, e = 1, and loss in KE = 0.
That is, KE is conserved in an elastic collision.
(ii) For a perfectly inelastic collision, e = 0, and
Loss in KE = \(\frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(u_1-u_2)^2\) which is maximum.
If the collision is partially inelastic, then the ratio of their final velocities in terms of coefficient of restitution e :
Consider a head-on (one-dimensional) collision of two identical objects, moving with constant initial velocities u1 and u2. Since they are identical,
m1 = m2 = m
If v1 and v2 are their velocities after the collision, then by the principle of conservation of linear momentum, *
m1u1 + m2u2 = m1v1 + m2v2
∴ u1 + u2 = v1 + v2
and the coefficient of restitution,
e = \(\frac{v_2-v_1}{u_1-u_2}\) = \(\frac{v_2-v_1}{u_1}\) ….Since the target was at rest, u2 = 0.
∴ u1 = v1 + v2 …..(1)
and v2 – v1= eu1 ...(2)
∴ \(\frac{1}{e}=\frac{v_1+v_2}{v_2-v_1}\)
∴ \(\frac{v_2}{v_1}=\frac{1+e}{1-e}\)
∴ \(\frac{v_1}{v_2}=\frac{1-e}{1+e}\) (0<e<1)
is the required expression.
If two particles undergo a head-on inelastic collision, then their final velocities in terms of their masses, initial velocities and the coefficient of restitution :
Consider a head-on (one-dimensional) collision of two particles, of masses m1 and m2, moving with constant initial velocities u1 and u2. If v1 and v2 are their velocities after the collision, then by the principle of conservation of linear momentum,
m1u1 + m2u2 = m1v1 + m2v2 …. (1)
The coefficient of restitution for the inelastic collision,
0 < e = \(\frac{v_2-v_1}{u_1-u_2}\) < 1
∴ v2 = v1 + eu1 − eu2 ...(2)
Substituting this value of v2 in Eq. (1),
m1u1 + m2u2 = m1v1 + m2(v1 + eu1 − eu2)
= m1v1 + m2v1 + em2u1 − em2u2
∴ m1u1 - em2u1 + m2u2 + em2u2 = (m1 + m2)v1
∴ v1 = \((\frac{m_1-em_2}{m_1+m_2})u_1+(\frac{m_2(e+1)}{m_1+m_2})u_2\) ……. (3)
Similarly, from Eq. (2), v1 = v2 − eu1 + eu2, which on substitution into Eq. (1) gives
v2 = \((\frac{m_1(1+e)}{m_1+m_2})u_1+(\frac{m_2-em_1}{m_1+m_2})u_2\) ……. (4)
Equations (3) and (4) give the required expressions.
Equations (3) and (4) can also be written as
v1 = \(\frac{em_2(u_2-u_1)+m_1u_1+m_2u_2}{m_1+m_2}\) and
v2 = \(\frac{em_1(u_1-u_2)+m_1u_1+m_2u_2}{m_1+m_2}\)
The impulse of a force :
For a force \(vec{F}\) which is constant over the time interval Δt during which it acts, the impulse of the force is defined as the product \(\vec{F}\)Δt :
\(\vec{J}\) = \(\vec{F}\)Δt
Newton's second law of motion, which duplicates the first law with quantitative precision, states that the change in momentum of a body equals the impulse of the applied force and is made in the direction of that force.
Then,
\(\vec{J}=\vec{dp}=\vec{p_f}-\vec{p_i}=m(\vec{v}-\vec{u})\)
where m is the mass of the body \(\vec{p_i}\) and \(\vec{p_f}\) are the initial and final momenta of the body over the time interval of the impulse.
For a time-varying force \(\vec{F}(t)\), whose magnitude over the interval Δt is given by the curve in Fig. (a), the impulse of the force is given by the area under the curve :
\(\vec{J}=\int_{t_i}^{t_f}\vec{F}dt\)

For a time-varying force, the magnitude of the impulse can also be written as
J = Fav Δt
where Fav is the average force that would impart the same impulse as the variable force over the time interval, i.e., the area Fav Δt of the rectangle in Fig. (b) is equal to the area under the curve in Fig. (a).
Dimensions : [Impulse] = [force]['dme]
= [mass] [acceleration] [time]
= [mass][vel0city]
= [MLT−1]
SI unit : The newton-second, N.s (= kg.m/s)
Necessity of defining impulse:
In many cases, an appreciable force acts for an extremely small interval of time (too small to measure the force and the time independently). However, change in the momentum due to this force is noticeable and can be measured. This change is defined as impulse of the force. Thus, it is convenient to define the change in momentum itself as a physical quantity.
Q. Two particles undergo a head-on inelastic collision. Assuming the expressions for their final velocities in terms of the reduced mass of the system, coefficient of restitution and the velocity of approach, obtain the expressions for the impulses on the two particles.
Ans. Two particles of masses ml and m2 move with initial velocities u1 and u2 along the same straight line such that particle 1 collides head-on inelastically with particle 2.
Let e be the coefficient of restitution of the collision. Their respective velocities after the collision are
∴ v1 = \((\frac{m_1-em_2}{m_1+m_2})u_1+(\frac{m_2(e+1)}{m_1+m_2})u_2\)
= \(\frac{em_2(u_2-u_1)+m_1u_1+m_2u_2}{m_1+m_2}\) …….(1)
v2 = \((\frac{m_1(1+e)}{m_1+m_2})u_1+(\frac{m_2-em_1}{m_1+m_2})u_2\)
= \(\frac{em_1(u_1-u_2)+m_1u_1+m_2u_2}{m_1+m_2}\) …….(2)
The magnitude of the impulse on particle 2 by 1 is
J21 = Δp2 = m2v2 − m2u2
Substituting for v2 from Eq. (2),
J21 = \(\frac{em_1m_2u_1-em_1m_2u_2+m_1m_2u_1+m_2^2u_2-m_1m_2u_2-m_2^2u_2}{m_1+m_2}\)
= \(\frac{m_1m_2}{m_1+m_2}[e(u_1-u_2)+(u_1-u_2)]\)
= \(\frac{m_1m_2}{m_1+m_2}[(u_1-u_2)+(1+e)]\)
= μ (u1 − u2)(1 +e) ….....(3)
where u1 − u2 is the velocity of approach of particle 1 relative to particle 2 and
μ = is the reduced mass of the system.
Similarly, the magnitude of the impulse on particle 1 by 2 is
J12 = Δp1 = m1v1 − m1u1
Substituting for v1 from Eq. (2),
J12 = \(\frac{em_1m_2u_2-em_1m_2u_1+m_1m_2u_2+m_1^2u_1-m_1m_2u_1-m_1^2u_1}{m_1+m_2}\)
= \(\frac{m_1m_2}{m_1+m_2}[e(u_2-u_1)+(u_2-u_1)]\)
= \(\frac{m_1m_2}{m_1+m_2}[(u_2-u_1)+(1+e)]\)
= μ (u2 − u1)(1 +e) ….....(4)
where u2 − u1 is the velocity of approach of particle 2 relative to particle 1
Expectedly J12 = −J21
Collision in two dimensions, i.e., a nonhead-on collision:
In this case, the direction of at least one initial velocity is not along the line of impact.
Consider an oblique impact/collision of two smooth spheres, moving with velocities \(\vec{u_1}\) and \(\vec{u_2}\) . At the moment of impact, the two spheres have a common tangent, which is perpendicular to the line through the centres of the two spheres.
The line through the centres of the two spheres is called the line of impact. The mutual forces between the two spheres act along the line of impact, so the impulse affecting each sphere also acts along the line of impact.
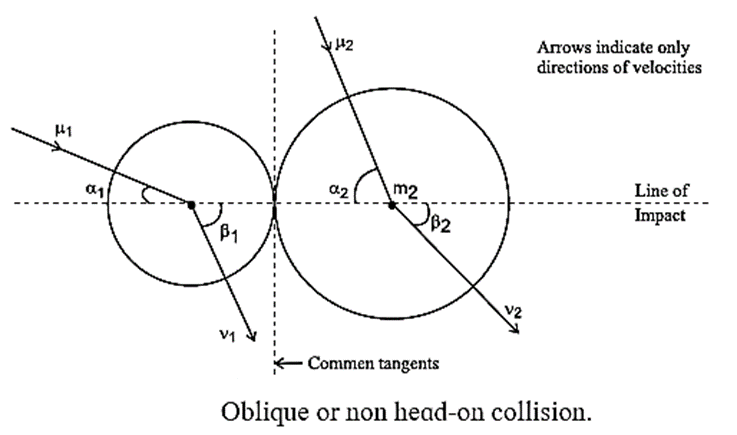
Let us consider the line of impact as the x-axis and the common tangent as the y-axis, see above Fig.
Then, according to the law of conservation of linear momentum along the line of impact,
m1u1x + m2u2x = m1v1x + m2v2x
m1u1 cos α1 + m2u2 cos α2 = m1v1x cos β1 + m2v2 cos β2 …… (1)
The components of the velocities along the common tangent are unchanged in the impact.
u1y = v1y and u2y = v2y
∴ u1 sin α1 = v1 sin β1 ….(2)
and u2 sin α2 = v2 sin β2 ……(3)
Newton's law of restitution applies to the components of the velocities of the spheres parallel to the line of impact. Thus, the coefficient of restitution between the spheres is
e = \(\frac{v_{2x}-v_{1x}}{u_{2x}-u_{1x}}\)
= \(-\frac{v_2cosβ_2-v_1cosβ_1}{u_2cosα_2-u_1cosα_1}\)
= \(\frac{v_2cosβ_2-v_1cosβ_1}{u_1cosα_1-u_2cosα_2}\) ….(4)
Equations (1), (2), (3) and (4) are solved for the four unknowns v1, v2, β1 and β2. The magnitude of the impulse on sphere 2 by 1 is
J12 = μ (u1 cos α1 − u2 cos α2)(1+e)
and the magnitude of the impulse on sphere 1 by 2 is
J21 = μ (u2 cos α2 − u1 cos α1)(1+ e)
where μ = \(\frac{m_1m_2}{m_1+m_2}\) is the reduced mass of the system.
The Loss in KE = \(\frac{1}{2}\) μ (u1 − u2)2(1 – e2)
Main Page : – Maharashtra Board Class 11th-Physics – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter 3: Motion in a Plane – Online Notes
Next Chapter : Chapter 5: Gravitation – Online Notes
Nice 👍👍😊👍👍😊👍👍😊👍👍😊👍👍😊