Wave Optics
Maharashtra Board-Class-12th-Physics-Chapter-7
Solution-Part-1
|
Solution : Part-1
|
Question 1.
Choose the correct option.
i) Which of the following phenomenon proves that light is a transverse wave?
(A) reflection
(B) interference
(C) diffraction
(D) polarization
(D) polarization
ii) Which property of light does not change when it travels from one medium to another?
(A) velocity
(B) wavelength
(C) amplitude
(D) frequency
(D) frequency
iii) When unpolarized light is passed through a polarizer, its intensity
(A) increases
(B) decreases
(C) remains unchanged
(D) depends on the orientation of the polarizer
(B) decreases
iv) In Young’s double slit experiment, the two coherent sources have different intensities. If the ratio of maximum intensity to the minimum intensity in the interference pattern produced is 25:1. What was the ratio of intensities of the two sources?
(A) 5:1 (B) 25:1 (C) 3:2 (D) 9:4
(D) 9:4
v) In Young’s double slit experiment, a thin uniform sheet of glass is kept in front of the two slits, parallel to the screen having the slits. The resulting interference pattern will satisfy.
(A) The interference pattern will remain unchanged
(B) The fringe width will decrease
(C) The fringe width will increase
(D) The fringes will shift.
(A) The interference pattern will remain unchanged
Question 2.
Answer in brief.
i) What are primary and secondary sources of light?
The Sun, moon, stars, light bulb, etc. are the several sources of light around us, These can be classified into primary and secondary sources of light. Primaly sources of light :The sources that emit light on their own are called primary sources. This emission of light may be due to Secondary sources of light : Some sources are not self luminous, i.e., they do not emit light on their own, but reflect or scatter the light incident on them. Such sources of light are called secondary sources, e.g. the moon, the planets, objects such as humans, animals, plants, etc. These objects are visible due to reflected light. Many of the sources that we see around are secondary sources and most of them are extended sources.
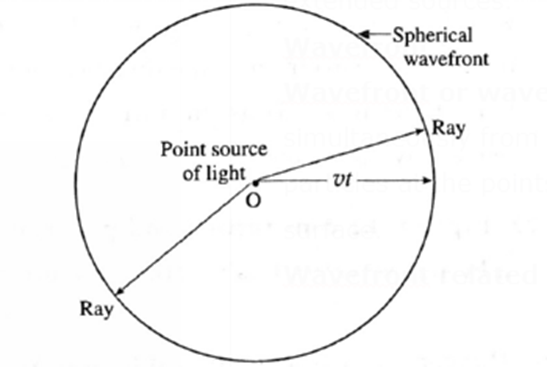
ii) What is a wavefront? How is it related to rays of light? What is the shape of the wavefront at a point far away from the source of light?
Wavefront or wave surface : The locus of all points where waves starting simultaneously from a source reach at the same instant of time and hence the particles at the points oscillate with the same phase, is called a wavefront or wave surface. Wavefront related to rays of light : Consider a point source of light O in a homogeneous isotropic medium in which the speed of light is v. The source emits light in all directions. In time t, the disturbance (light energy) from the source, covers a distance vt in all directions, i.e, it reaches out to all points which are at a distance vt from the point source. The locus of these points which are in the same phase is the surface of a sphere with the centre O and radius vt. It is a spherical wavefront. In a given medium, a set of straight lines can be drawn which are perpendicular to the wavefront. According to Huygens, these straight lines are the rays of light. Thus, rays are always normal to the wavefront. In the case of a spherical wavefront, the rays are radial. Shape of the wavefront at a point far away from the source of light : If a wavefront has travelled a large distance away from the source, a small portion of this wavefront appears to be plane. This part is a plane wavefront.
iii) Why are multiple colours observed over a thin film of oil floating on water? Explain with the help of a diagram.
Interference due to thin films: The brilliant colours of thin oil films on the surface of water are due to the interference of light waves reflected from the upper and lower surfaces of the film. The two rays have a path difference which depends on the point on the film that is being viewed. This is shown in the figure. 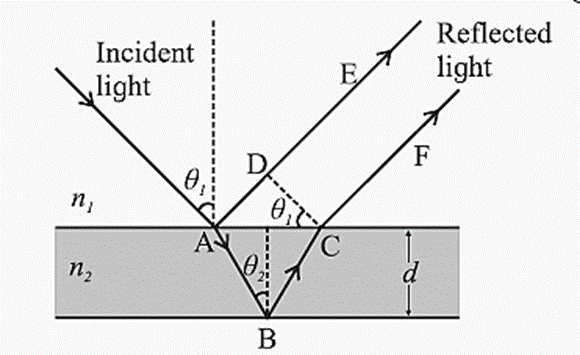
iv) In Young's double slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
v) Explain, what is optical path length ?. How is it different from actual path length?
Optical path length : Consider, a light wave of angular frequency ω and wave vector k travelling through vacuum along the x-direction. The phase of this wave is (kx—ωt) The speed of light in vacuum is c and that in medium is v k = \(\frac{2π}{λ}=\frac{2πν}{νλ}=\frac{ω}{v} \) as ω = 2πν and v = νλ, where ν is the frequency of light. If the wave travels a distance Δx, its phase, changes by ΔΦ = kΔx = ωΔx/v. Similarly, if the wave is travelling in vacuum, K = ω/c and ΔΦ = ωΔx/c Now, consider a wave travelling a distance Δx in the medium, the phase difference generated is, ΔΦ’=k'Δx = ωnΔx/c = ωΔx’/c …...(1) where Δx’ = nΔx ... (2) The distance nΔx is called the optical path length of the light in the medium; it is the distance the light would have travelled in the same time t in vacuum (with the speed c). The optical path length in a medium is the corresponding path in vacuum that the light travels in the same time as it takes in the given medium. Now, speed = distance/time ∴ time = distance/speed ∴ t = dmedium/vmedium = dvaccum/vvaccum Hence the optical path = dvaccum = \(\frac{v_{vaccum}}{v_{mediuam}}×d_{medium}\) = n x dmedium Thus, a distance d travelled in a medium of refractive index n introduces a path difference = nd — d = d(n — 1) over a ray travelling equal distance through vacuum. Two waves interfere constructively when their optical path lengths are equal or differ by integral multiples of the wavelength.
Question 3.
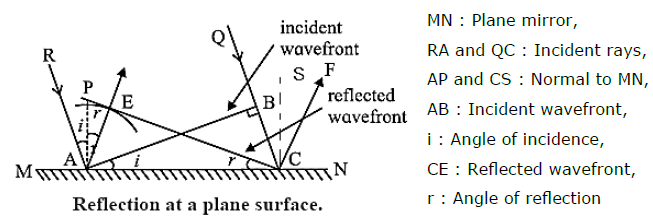
Derive the laws of reflection of light using Huygens’ principle.
Consider a plane wavefront AB of monochromatic light incident obliquely at an angle i on a plane mirror MN. The wavefront AB touches the reflecting surface MN at A at time t = 0. Let v be the speed of light in the medium. When wavefront AB is incident on the mirror, at first, point A becomes a secondary source and emits secondary waves in the same medium. If T is the time taken by the incident wavefront to travel from B to C, then BC = vT. During this time, the secondary wave originating at A covers the same distance, so that the secondary spherical wavelet has a radius vT at time T. To construct the reflected wavefront, a hemisphere of radius vT is drawn from point Draw a tangent EC to the secondary wavelet. As all points on EC are in the same phase of wave motion, EC represents the reflected wavefront. The arrow AE shows the direction of propagation of the reflected wave. AP is the normal to MN at A, ∠ RAP = i = angle of incidence and ∠ PAE = r = angle of reflection In Δ ABC and Δ AEC, AC is common, AE =BC and ∠ ABC = ∠ AEC = 90° Δ ABC and Δ AEC are congruent. ∠ ACE = ∠ BAC = i …….(1) Also, as AE is perpendicular to CE and AP is perpendicular to AC, ∠ ACE = ∠ PAE =r ...(2) From Eqs (1) and (2), i = r Thus, the angle of incidence is equal to the angle of reflection. This is the first law of reflection. Also, it can be seen from the figure that the incident ray and reflected ray lie on the opposite sides of the normal to the reflecting surface at the point of incidence and all of them lie in the same plane. This is the second law of reflection. Thus, the laws of reflection of light can be deduced by Huygens’ construction of a plane wavefront.
Question 4.
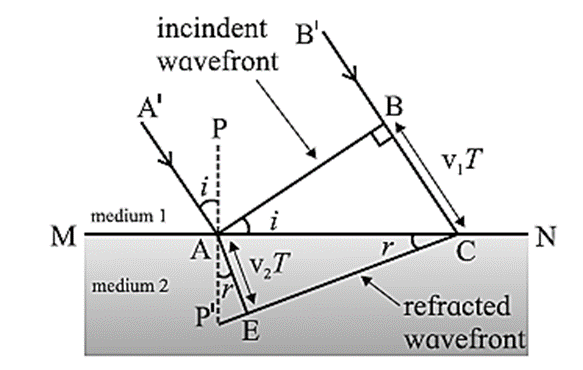
Derive the laws of refraction of light using Huygens’ principle.
Consider a plane wavefront AB of monochromatic light propagating in the direction A’A incident obliquely at an angle i on a plane refracting surface MN. This plane refracting surface MN separates two uniform and optically transparent mediums. Let v1 and v2 be the speeds of light in medium 1 (say, a rarer medium) and medium 2 (a denser medium) respectively. When the wavefront reaches MN at point A at t = 0, A becomes a secondary source and emits secondary waves in the second medium, while ray B’B reaches the surface MN at C at time t = T. Thus, BC = v1T. During the time T, the secondary wavelet originating at A covers a distance AE in the denser medium with radius v2T. As all the points on CE are in the same phase of wave motion, CE represents the refracted wavefront in the denser medium. CE is the tangent to the secondary wavelet starting from A. It is also a common tangent to all the secondary wavelets emitted by points between A and C. PP’ is the normal to the boundary at A. ∠ A’AP = ∠ BAC = the angle of incidence (i) and ∠ P’AE = ∠ ACE = the angle of refraction (r). From Δ ABC and Δ AEC, sin i = \(\frac{BC}{AC}\) and sin r = \(\frac{AE}{AC}\) ∴ \(\frac{sin\,i}{sin\,r}=\frac{BC/AC}{AE/AC}=\frac{BC}{AE}=\frac{v_1T}{v_2T}=\frac{v_1}{v_2}\) By definition, the refractive index of medium 2 with respect to medium 1, 1n2 = \(\frac{n_2}{n_1}=\frac{v_1}{v_2}\) ∴ \(\frac{n_2}{n_1}=\frac{sin\,i}{sin\,r}\) n1 sin i = n2 sin r ….. (1) Here, n1 and n2 are the absolute refractive indices of medium 1 and medium 2 respectively. Eq. (1) is Snell's law of refraction. Also, it can be seen from the figure, that the incident ray and the refracted ray lie on the opposite sides of the normal and all three of them lie in the same plane. Thus, the laws of refraction of light can be deduced by Huygens’ construction of a plane wavefront. If v1 > v2, i.e. n1 < n2, then r < i (bending of the refracted ray towards the normal).
Question 5.
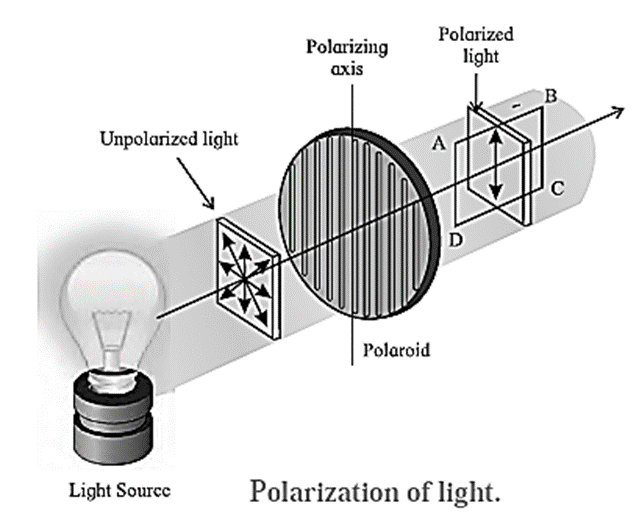
Explain what is meant by polarization and derive Malus’ law.
According to the electromagnetic theory of light, a light wave consists of electric and magnetic fields vibrating at right angles to each other and to the direction of propagation of the wave. If the vibrations of in a light wave are in all directions perpendicular to the direction of propagation of light, the wave is said to be unpolarized. If the vibrations of the electric field in a light wave are confined to a single plane containing the direction of propagation of the wave so that its electric field is restricted along one particular direction at right angles to the direction of propagation of the wave, the wave is said to be plane-polarized or linearly polarized. This phenomenon of restricting the vibrations of light, i.e., of the electric field vector in a particular direction, which is perpendicular to the direction of the propagation of the wave is called polarization of light. Consider an unpolarized light wave travelling along the x-direction. Let c, n and λ be the speed, frequency and wavelength, respectively, of the wave. The magnitude of its electric field (\(\vec{E}\) ) is, E = E0 sin (kx − ωt), where E0 = Emax = amplitude of the wave, ω = 2pn = angular frequency of the wave and k = 2p/λ = magnitude of the wave vector or propagation vector. The intensity of the wave is proportional to |E0|2. The direction of the electric field can be anywhere in the y-z plane. This wave is passed through two identical polarizers as shown in below Fig. When a wave with its electric field inclined at an angle Φ to the axis of the first polarizer is passed through the polarizer, the component E0 cos Φ will pass through it. The other component E0 sin Φ which is perpendicular to it will be blocked. Now, after passing through this polarizer, the intensity of this wave will be proportional to the square of its amplitude, i.e., proportional to |E0 cos Φ|2. The intensity of the plane-polarized wave emerging from the first polarizer can be obtained by averaging |E0 cos Φ|2 over all values of Φ between 0 and 180°. The intensity of the wave will be proportional to ½|E0|2 as the average value of cos2Φ over this range is Thus the intensity of an unpolarized wave reduces by half after passing through a polarizer. When the plane-polarized wave emerges from the first polarizer, let us assume that its electric field ( ) is along the y-direction. See Fig . Thus, this electric field is, \(\vec{E}\) =\(\hat{j}\) E10 sin (kx—ωt) …..(1) where, E10 is the amplitude of this polarized wave. The intensity of the polarized wave, I1 ∝ lE10l2 …….(2) Now this wave passes through the second polarizer whose polarization axis (transmission axis) makes an angle θ with the y-direction. This allows only the component E10 cos θ to pass through it. Thus, the amplitude of the wave which passes through the second polarizer is E20 = E10 cos θ and its intensity, I2 ∝ |E20|2 ∴ I2 ∝ |E20|2 cos2θ ∴ I2 = I1 cos2θ ….(3) Thus, when plane-polarized light of intensity I1 is incident on the second identical polarizer, the intensity of light transmitted by the second polarizer varies as cos2θ, i.e., I2 = I1 cos2θ, where θ is the angle between the transmission axes of the two polarizers. This is known as Malus’ law.
Question 6.
What is Brewster’s law? Derive the formula for Brewster angle.
Brewster's law : The tangent of the polarizing angle is equal to the refractive index of the reflecting medium with respect to the surrounding (1n2). If θB is the polarizing angle, tan θB = 1n2 = \(\frac{n_2}{n_1}\) Here n1 is the absolute refractive index of the surrounding and n2 is that of the reflecting medium. The angle θB is called the Brewster angle. Derivation of formula for Brewster angle Consider a ray of unpolarized monochromatic light incident at an angle θB on a boundary between two transparent media as shown in Fig. Medium 1 is a rarer medium with refractive index n1 and medium 2 is a denser medium with refractive index n2. Part of incident light gets refracted and the rest gets reflected. The degree of polarization of the reflected ray varies with the angle of incidence. The electric field of the incident wave is in the plane perpendicular to the direction of propagation of incident light. This electric field can be resolved into a component parallel to the plane of the paper, shown by double arrows, and a component perpendicular to the plane of the paper shown by dots, both having equal magnitude. Generally, the reflected and refracted rays are partially polarized, i.e., the two components do not have equal magnitude. In 1812, Sir David Brewster discovered that for a particular angle of incidence. θB, the reflected wave is completely plane-polarized with its electric field perpendicular to the plane of the paper while the refracted wave is partially polarized. This particular angle of incidence (θB) is called the Brewster angle. For this angle of incidence, the refracted and reflected rays are perpendicular to each other. For angle of refraction θr, θB + θr = 90° ...(1) From Snell's law of refraction, n1 sin θB = n2 sin θr ….(2) From Eqs. (1) and (2), we have, n1 sin θB = n2 sin(90°— θB) = n2 cos θB ∴ θB = tan-1\(\frac{n_2}{n_1}\) This is called Brewster's law.
Question 7.
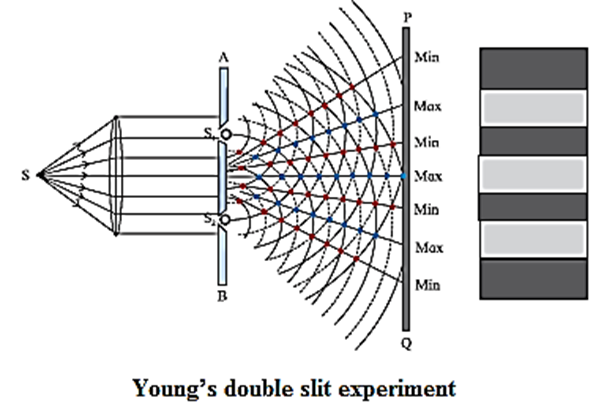
Describe Young’s double slit interference experiment and derive conditions for occurrence of dark and bright fringes on the screen. Define fringe width and derive a formula for it.
Young’s Double Slit Experiment: In this experiment, a plane wavefront is made to fall on an opaque screen AB having two similar narrow slits S1 and S2. Conditions for occurrence of dark and bright fringes on the screen : (Consider Young's double—slit experimental set up.) Two narrow coherent light sources are obtained by wavefront splitting as monochromatic light of wavelength A emerges out of two narrow and closely spaced, parallel slits S1 and S2 of equal widths. The separation S1S2 = d is very small. The interference pattern is observed on a screen placed parallel to the plane of S1S2 and at considerable distance D (D >> d) from the slits. OO’ is the perpendicular bisector of segment S1S2, Fig. Consider, a point P on the screen at a distance y from O’ (y << D). The two light waves from S1 and S2 reach P along paths S1P and S2P, respectively. If the path difference (Δl) between S1P and SZP is an integral multiple of λ, the two waves arriving there will interfere constructively producing a bright fringe at P. On the contrary, if the path difference between S1P and S2P is half integral multiple of λ, there will be destructive interference and a dark fringe will be produced at P. From above Fig. (S2P)2 = (S2S2’)2 + (PS2’)2 = (S2S2’)2 + (PO’ + O’ S2’)2 = D2 + \((y+\frac{d}{2})^2\) ……. (1) and (S1P)2 =(S1S1’)2 + (PS1’)2 =(S1S1’)2 + (PO’—O’ S1’)2 = D2 + \((y-\frac{d}{2})^2\) …… (2) (S2P)2 − (S1P)2 = \([D^2 + (y-\frac{d}{2})^2]\) – \([D^2 +(y-\frac{d}{2})^2]\) ∴ (S2P + S1P)(S2P − S1P) = [D2 + y2 + \(\frac{d^2}{2}\) + yd] – [D2 + y2 + \(\frac{d^2}{2}\) – yd] = 2yd ∴ S2P − S1P = Δl = 2yd/(S2P + S1P) In practice, D >> y and D >> d S2P + S1P ≈ 2D Path difference, Δl = (S2P − S1P) ≈ \(2\frac{yd}{2D} = y\frac{d}{D}\) ….. (3) Expression for the fringe width (or band width) ; The distance between consecutive bright (or dark) fringes is called the fringe width (or band width) W, Point P will be bright (maximum intensity), if the path difference, Δl = yn \(\frac{d}{D}\) = n λ where n = 0, 1, 2, 3..., Point P will be dark (minimum intensity equal to zero), if ym \(\frac{d}{D}\) = (2m — 1)\(\frac{λ}{2}\) , where, m = 1, 2, 3..., Thus, for bright fringes (or bands), yn = 0, \(\frac{λD}{d}\) , \(\frac{2λD}{d}\) …. and for dark fringes (or bands), ym = \(\frac{λD}{2d}\) , \(\frac{3λD}{2d}\), \(\frac{5λD}{2d}\) …. These conditions show that the bright and dark fringes (or bands) occur alternately and are equally spaced. For Point O’, the path difference (S2O’ — S1O’) = 0. Hence, point O’ will be bright. It corresponds to the centre of the central bright fringe (or band). On both sides of O’, the interference pattern consists of alternate dark and bright fringes (or band) parallel to the slit. Let yn and yn +1, be the distances of the nth and (n + 1)th bright fringes from the central bright fringe. . ∴ yn \(\frac{d}{D}\) = n λ , ∴ yn = \(\frac{nλD}{d}\) ….. (4) And \(\frac{y_{n+1}d}{D}\) = (n+1)λ, ∴ yn+1 = \(\frac{(n+1)λD}{d}\) ….. (5) The distance between consecutive bright fringes = yn+1 − yn = \(\frac{λD}{d}[(n+1)-n]\) = \(\frac{λD}{d}\) …….(6) Hence, the fringe width, ∴ W = Δy = yn+1 − yn = \(\frac{λD}{d}\) (fo rbright fringes) ...(7) Alternately, let ym and ym +1 be the distances of the m th and (m + 1)th dark fringes respectively from the central bright fringe. ∴ \(\frac{y_md}{D}\) = (2m—1)\(\frac{λ}{2}\) and \(\frac{y_{m+1}d}{D}\)= [2(m+1)—1]\(\frac{λ}{2}\) = (2m+1)\(\frac{λ}{2}\) …. (8) ∴ ym = (2m—1) \(\frac{λD}{2d}\) and ym +1 = (2m+1)\(\frac{λD}{2d}\) The distance between consecutive dark fringes, ym+1—ym = \(\frac{λD}{2d}\)[(2m+1)-(2m-1)] = \(\frac{λD}{d}\)...(10) ∴ W = ym+1 − ym = \(\frac{λD}{d}\)(for dark fringes) …..(11) Eqs. (7) and (11) show that the fringe width is the same for bright and dark fringes.

Question 8.
What are the conditions for obtaining good interference pattern? Give reasons.
The following conditions have to be satisfied for the interference pattern to be steady and clearly visible. (1) The two sources of light should be coherent. (2) The two sources of light must be monochromatic : (3) The two interfering waves must have the same amplitude : (4) The separation between the two light sources must be small in comparison to the distance between the plane containing the slits and the observing screen: (5) The two light sources should be narrow : (6) The interfering light waves should be in the Same state of polarization :
Question 9.
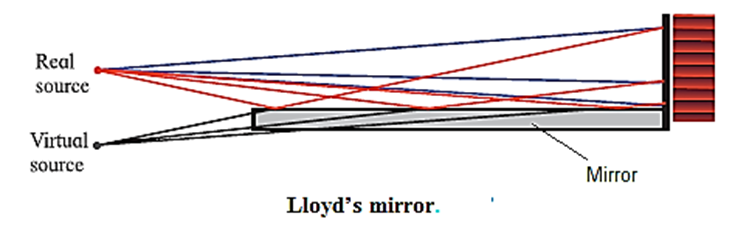
What is meant by coherent sources? What are the two methods for obtaining coherent sources in the laboratory?
Coherent sources : Two sources which emit waves of the same frequency having a constant phase difference, independent of time, are called coherent sources. In the laboratory, coherent sources can be obtained by 'using (1) Lloyd's mirror and (2) Fresnel's bi-prism. Lloyd's mirror : A plane polished mirror is kept at some distance from the source of monochromatic light and light is made incident on the mirror at a grazing angle. Fresnel’s Biprism : It is a single prism having an obtuse angle of about 178° and the other two angles of about 1° each. The biprism can be considered as made of two thin prisms of very small retracting angle of about 1°.
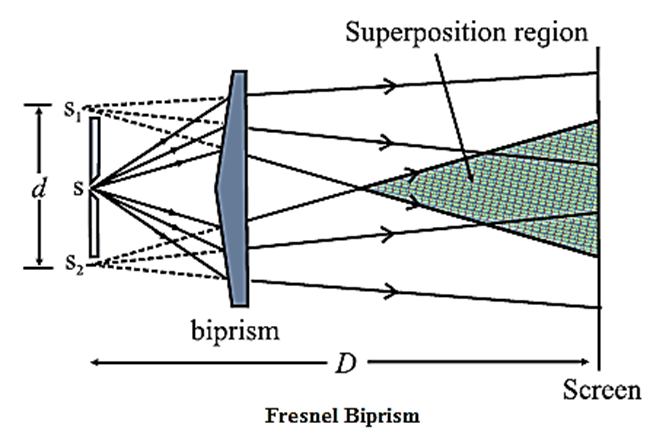
Question 10.
What is diffraction of light? How does it differ from interference? What are Fraunhoffer and Fresnel diffractions?
Phenomenon of diffraction of light : When light passes by the edge of an obstacle or through a small opening or a narrow slit and falls on a screen, the principle of rectilinear propagation of light from geometrical optics predicts a sharp shadow. However, it is found that some of the light deviates from its rectilinear path and penetrates into the region of the geometrical shadow. This is a general characteristic of wave phenomena, which occurs whenever a portion of the wavefront is obstructed in some way. This bending of light waves at an edge into the region of geometrical shadow is called diffraction of light. Differences between interference and diffraction : Diffraction can be classified into two types depending on the distances involved in the experimental setup :
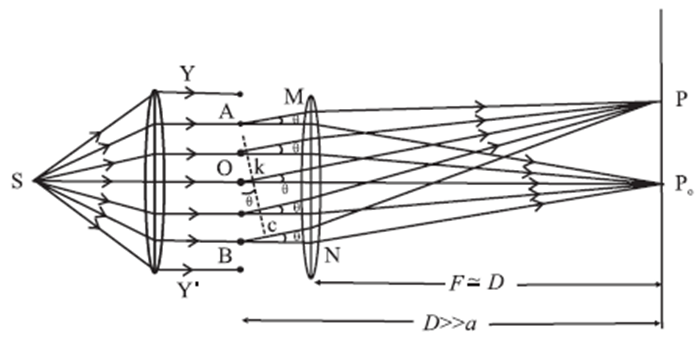
Question 11.
Derive the conditions for bright and dark fringes produced due to diffraction by a single slit.
Fraunhofer diffraction pattern due to a single slit : When a parallel beam of monochromatic light of wavelength λ illuminates a single slit of finite width a, we observe on a screen some distance from the slit, a broad pattern of alternate dark and bright fringes. The pattern consists of a central bright fringe, with successive dark and bright fringes of diminishing intensity on both sides. This is called the diffraction pattern of a single slit. Consider a single slit illuminated with a parallel beam of monochromatic light perpendicular to the plane of the slit. The diffraction pattern is obtained on a screen at a distance D ( >> a) from the slit and at the focal plane of the convex lens, see Fig. Location of minima and maxima: We can imagine the single slit as being made up of a large number of Huygens’ sources evenly distributed over the width of the slit. Then the maxima and minima of the pattern arise from the interference of the various Huygens’ wavelets Fig. - Fraunhofer diffraction due to a single slit Now, imagine the single slit as made up of two adjacent slits, each of width a/2. Since, the incident plane wavefronts are parallel to the plane of the slit, all the Huygens sources at the slit will be in phase. They will therefore also in phase at the point P0 on the screen, where P0 is equidistant from all the Huygens sources. At P0, then, we get the central maximum. Expressions for the positions of the intensity minima and maxima : For the first minimum of intensity on the screen, the path difference between the waves from the Huygens sources A and O (or O and B) is λ/2, which is the condition for destructive interference. Suppose, the nodal line OP for the first minimum subtends an angle θ at the slit; θ is very small. With P as the centre and PA as radius, strike an arc intersecting PB at C. Since, D >> a, the arc AC can be considered a straight line at right angles to PB. Then, Δ ABC is a right-angled triangle similar to Δ OP0P. This means that, ∠ BAC = 0 ∴ BC = a sin θ Difference in path length, ∴ BC = PB − PA = (PB—PO) + (PO—PA) = \(\frac{λ}{2}+\frac{λ}{2}\) = λ ∴ a sin θ = λ ∴ sin θ ≈ θ = λ/a …....(1) ….('.' θ is very small and in radian) The other nodal lines of intensity minima can be understood in a similar way. In general, then, for the mth minimum (m = ±1, ±2, ±3, ...). θm = mλ/a ...(mth minimum) …..(2) as θm is very small and in radian. Between the successive minima, the intensity rises to secondary maxima when the path difference is an odd-integral multiple of λ/2 a sin θm = (2m+1)\(\frac{λ}{2}\) = (m+\(\frac{1}{2}\) ) λ i.e., at angles given by, θm ≈ sin θm = (m+\(\frac{1}{2}\))\(\frac{λ}{a}\) (mth secondary maximum)
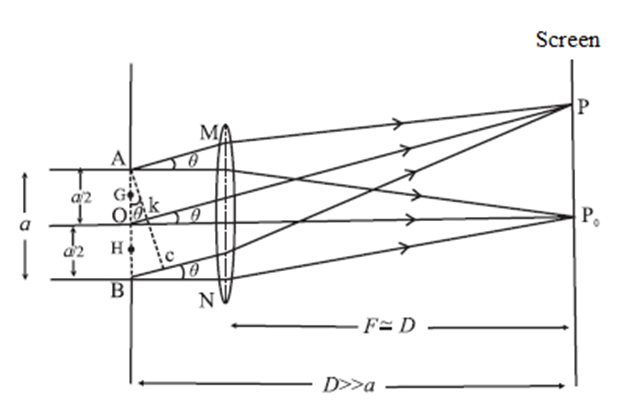
Question 12.
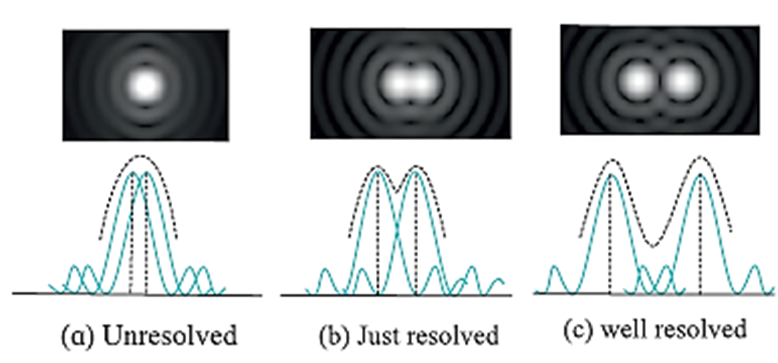
Describe Rayleigh’s criterion for resolution. Explain it for a telescope and a microscope.
Rayleigh’s Criterion for Limit of Resolution (or for Resolving Power): Two overlapping diffraction patterns due to two point sources are acceptably or just resolved if the centre of the central peak of one diffraction pattern is as far as the first minimum of the other pattern. The ‘sharpness’ of the central maximum of a diffraction pattern is measured by the angular separation between the centre of the peak and the first minimum. It gives the limit of resolution. Resolving Power of a Microscope: Resolving Power of a Telescope:
Main Page : – Maharashtra Board Class 12th-Physics – All chapters notes, solutions, videos, test, pdf. Previous Chapter : Chapter-6-Superposition of Waves –Online Solution Next Chapter : Chapter-8- Electrostatics – Online Solution
We reply to valid query.